沪科版八年级上册15.3等腰三角形(第2课时) 课件(共18张PPT)
文档属性
| 名称 | 沪科版八年级上册15.3等腰三角形(第2课时) 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 07:13:39 | ||
图片预览






文档简介
(共18张PPT)
15.3 等腰三角形
第2课时 等腰三角形性质的应用
第15章 轴对称图形与等腰三角形
学习目标
1
2
掌握判定两个直角三角形全等的“HL”定理,运用定理进行相关的证明.(难点)
利用等腰三角形的性质进行相关的证明.(重点)
知识回顾
定理1:等腰三角形的两个底角相等(等边对等角).
定理2:等腰三角形顶角的平分线垂直平分底边.
等腰三角形顶角的平分线、底边上的中线和底边上的高“三线合一”.
推论:等边三角形的三个内角都相等,并且每一 个角都等于60°.
思考?
2.两个直角三角形全等的判定有哪些?
1.三角形全等的判定有哪些?
ASA SAS AAS SSS
ASA SAS AAS SSS HL
3.已知两边及其一边的对角分别相等,能否判定两个三角形全等?
若是两个直角三角形,则这两个三角形全等,否则,两个三角形不一定全等
新课导入
A
B
C
D
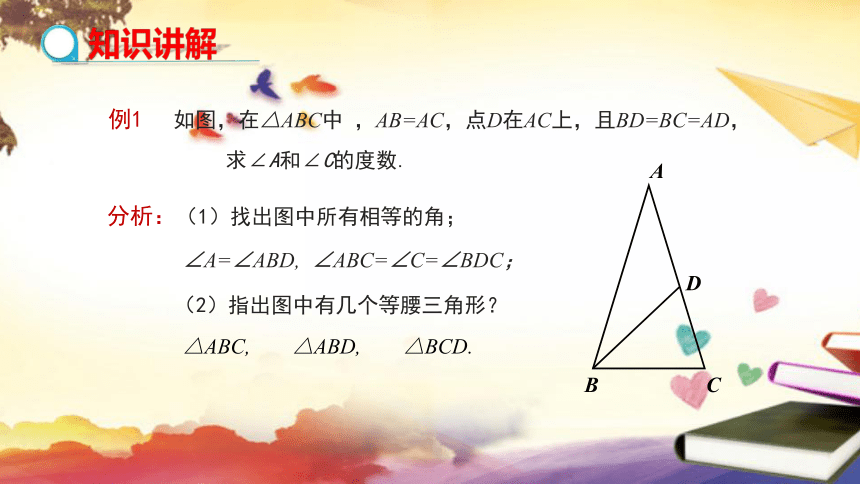
例1 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,
求∠A和∠C的度数.
分析:(1)找出图中所有相等的角;
(2)指出图中有几个等腰三角形?
∠A=∠ABD,
∠ABC=∠C=∠BDC;
△ABC,
△ABD,
△BCD.
知识讲解
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
(3)观察∠BDC 与∠A、∠ABD的关系,∠ABC、∠C 呢?
∠BDC= ∠A+ ∠ABD=2 ∠A=2 ∠ABD,
∠ABC= ∠BDC=2 ∠A,
∠C= ∠BDC=2 ∠A.
(4)设∠A=x,请把△ ABC的内角和用含x的式子表示出来.
∵ ∠A+ ∠ABC+ ∠C=180 °,∴ x+2x+2x=180 °.
A
B
C
D
解:∵AB=AC,BD=BC=AD,(已知)
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.(等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,(三角形的一个外角等于和它不相邻的两个内角的和)
∵ ∠ABC= ∠C=∠BDC=2x,
∴∠A+∠ABC+∠C=x+2x+2x=180 °,(三角形的内角和等于180°)
解方程,得x=36° ,
∴∠A=36°,∠ABC=∠C=72°.
x
⌒
2x
⌒
2x
⌒
⌒
2x
例2 求证:斜边和一条直角边分别相等的两个直角三角形全等.
已知:如图在Rt△ABC 中和Rt△A′B′C′中, AC
∠C= ∠C'=90°,AB= A′B′,AC= A′C′.
求证:Rt△ABC ≌R△ABC.
A
B
C
A′
B′
C′
A
B
C
A′
B′
C′
证明:在平面内移动Rt△ABC和Rt△A'B'C,使点A 和点A'、点C和点C '重合,点B和点B'在AC的两侧
∵∠BCB'=90°+90°=180°,(等式性质)
∴B,C,B′三点在一条直线上(平角的定义)
在△ABB'中
∵AB=AB′,(已知)
∴∠B=∠B′(等边对等角)
在Rt△ABC和Rt△AB'C中
∠B=∠B′,(已证)
AB=A'B',(已知)
∴RtABC≌Rt△AB′C′ (AAS)
∵ ∠ACB=∠ACB′,(已知)
例3 已知,△ABC 是等边三角形,D、E、F分别是AB、BC、AC上一点,且∠DEF=60°.
(1)如图1,若∠1=50°,求∠2;
(2)如图2,连接DF,若∠1=∠3,求证:DF∥BC.
分析:(1)根据等边三角形的性质和三角形的内角和解答;
(2)根据三角形的内角和和平角的定义以及平行线的判定解答.
A
B
C
D
E
F
A
B
C
D
E
F
1
2
1
2
3
图1
图2
解:(1)∵△ABC是等边三角形,
∴∠B=∠A=∠C=60°,
∵∠B+∠1+∠DEB=180°∠DEB+∠DEF+∠2=180°,
∵∠DEF=60°,
∴∠1+∠DEB=∠2+∠DEB,
∴∠2=∠1=50°;
(2)∵∠B+∠1+∠DEB=180°,∠FDE+∠3+∠DEF=180°,
又∵∠B=60°,∠DEF=60°,∠1=∠3,
∴∠FDE=∠DEB,
∴DF∥BC.
随堂训练
1.如图,在△ABC中,AB=BC,D为AC上一点,且DA=DB,CB=CD,则∠DBC的度数 .
解析:∵AB=BC,AD=BD,
∴∠A=∠C=∠ABD,
∵BC=CD,
∴∠CDB=∠CBD,
∵∠CDB=∠A+∠ABD=2∠C,
∴∠C+2∠C+2∠C=180°,
∴∠C=36°,
∴∠DBC=72°.
72°
A
B
C
D
2.如图,三角形ABC中,AC=BC,D是BC上的一点,连接 AD,DF平分∠ADC交∠ACB的外角∠ACE的平分线于F.
(1)求证:CF∥AB;
(2)若∠DAC=40°,求∠DFC的度数.
A
B
C
D
E
F
(1)证明:∵AC=BC,
∴∠ACE=∠ABC+∠CAB=2∠ABC,
∴∠ABC=∠CAB,
∵CF是∠ACE的平分线,∴∠ACE=2∠FCE,
∴2∠ABC=2∠FCE,∴∠ABC=∠FCE,
∴CF∥AB;
(2)∵CF是∠ACE的平分线,
∴∠ACE=2∠FCE=∠ADC+∠DAC,
∵DF平分∠ADC,∴∠ADC=2∠FDC,
∴2∠FCE=∠ADC+∠DAC=2∠FDC+∠DAC,
∴2∠FCE﹣2∠FDC=∠DAC,
∵∠DFC=∠FCE﹣∠FDC,
∴2∠DFC=2∠FCE﹣2∠FDC=∠DAC=40°,
∴∠DFC=20°.
3.如图所示,在Rt△ABC中,∠C=90°,BE是∠ABC的平分线,ED是AB边的垂直平分线.求∠A的度数.
解:∵BE 是∠ABC的平分线,
∴∠CBE=∠ABE,
∵ED是AB边的垂直平分线,
∴BE=AE,
∴∠EBD=∠EAB,
设∠A=x°,
则∠CBE=∠EBD=∠A=x°,
∵∠C=90°,
∴∠A+∠CBA=90°,
即3x=90°,
解得x=30°,
∴∠A=30°.
A
B
C
D
E
A
C
B
D
E
4. 求证:等腰三角形底边上的中点到两腰的距离相等.
F
已知:如图,在△ABC中,AB=AC,D为BC的中 点,DE ⊥ AB,DF ⊥AC.
求证: DE=DF.
证明: ∵AB=AC,∴∠ABC=∠ACB,
∵ D为BC的中 点, ∴BD=CD.
∵ DE ⊥ AB,DF ⊥AC,
∴∠DEB=∠DFC,
∴△EDB≌△FDC(AAS),
∴DE=CF.
课堂小结
等腰三角形的性质应用
等边对等角
三线合一
文字证明题
1.根据题意写出已知和求证;
2.画出符合题意的图形;
3.根据已知、求证写出证明过程.
求角的度数
15.3 等腰三角形
第2课时 等腰三角形性质的应用
第15章 轴对称图形与等腰三角形
学习目标
1
2
掌握判定两个直角三角形全等的“HL”定理,运用定理进行相关的证明.(难点)
利用等腰三角形的性质进行相关的证明.(重点)
知识回顾
定理1:等腰三角形的两个底角相等(等边对等角).
定理2:等腰三角形顶角的平分线垂直平分底边.
等腰三角形顶角的平分线、底边上的中线和底边上的高“三线合一”.
推论:等边三角形的三个内角都相等,并且每一 个角都等于60°.
思考?
2.两个直角三角形全等的判定有哪些?
1.三角形全等的判定有哪些?
ASA SAS AAS SSS
ASA SAS AAS SSS HL
3.已知两边及其一边的对角分别相等,能否判定两个三角形全等?
若是两个直角三角形,则这两个三角形全等,否则,两个三角形不一定全等
新课导入
A
B
C
D
例1 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,
求∠A和∠C的度数.
分析:(1)找出图中所有相等的角;
(2)指出图中有几个等腰三角形?
∠A=∠ABD,
∠ABC=∠C=∠BDC;
△ABC,
△ABD,
△BCD.
知识讲解
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
(3)观察∠BDC 与∠A、∠ABD的关系,∠ABC、∠C 呢?
∠BDC= ∠A+ ∠ABD=2 ∠A=2 ∠ABD,
∠ABC= ∠BDC=2 ∠A,
∠C= ∠BDC=2 ∠A.
(4)设∠A=x,请把△ ABC的内角和用含x的式子表示出来.
∵ ∠A+ ∠ABC+ ∠C=180 °,∴ x+2x+2x=180 °.
A
B
C
D
解:∵AB=AC,BD=BC=AD,(已知)
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.(等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,(三角形的一个外角等于和它不相邻的两个内角的和)
∵ ∠ABC= ∠C=∠BDC=2x,
∴∠A+∠ABC+∠C=x+2x+2x=180 °,(三角形的内角和等于180°)
解方程,得x=36° ,
∴∠A=36°,∠ABC=∠C=72°.
x
⌒
2x
⌒
2x
⌒
⌒
2x
例2 求证:斜边和一条直角边分别相等的两个直角三角形全等.
已知:如图在Rt△ABC 中和Rt△A′B′C′中, AC
∠C= ∠C'=90°,AB= A′B′,AC= A′C′.
求证:Rt△ABC ≌R△ABC.
A
B
C
A′
B′
C′
A
B
C
A′
B′
C′
证明:在平面内移动Rt△ABC和Rt△A'B'C,使点A 和点A'、点C和点C '重合,点B和点B'在AC的两侧
∵∠BCB'=90°+90°=180°,(等式性质)
∴B,C,B′三点在一条直线上(平角的定义)
在△ABB'中
∵AB=AB′,(已知)
∴∠B=∠B′(等边对等角)
在Rt△ABC和Rt△AB'C中
∠B=∠B′,(已证)
AB=A'B',(已知)
∴RtABC≌Rt△AB′C′ (AAS)
∵ ∠ACB=∠ACB′,(已知)
例3 已知,△ABC 是等边三角形,D、E、F分别是AB、BC、AC上一点,且∠DEF=60°.
(1)如图1,若∠1=50°,求∠2;
(2)如图2,连接DF,若∠1=∠3,求证:DF∥BC.
分析:(1)根据等边三角形的性质和三角形的内角和解答;
(2)根据三角形的内角和和平角的定义以及平行线的判定解答.
A
B
C
D
E
F
A
B
C
D
E
F
1
2
1
2
3
图1
图2
解:(1)∵△ABC是等边三角形,
∴∠B=∠A=∠C=60°,
∵∠B+∠1+∠DEB=180°∠DEB+∠DEF+∠2=180°,
∵∠DEF=60°,
∴∠1+∠DEB=∠2+∠DEB,
∴∠2=∠1=50°;
(2)∵∠B+∠1+∠DEB=180°,∠FDE+∠3+∠DEF=180°,
又∵∠B=60°,∠DEF=60°,∠1=∠3,
∴∠FDE=∠DEB,
∴DF∥BC.
随堂训练
1.如图,在△ABC中,AB=BC,D为AC上一点,且DA=DB,CB=CD,则∠DBC的度数 .
解析:∵AB=BC,AD=BD,
∴∠A=∠C=∠ABD,
∵BC=CD,
∴∠CDB=∠CBD,
∵∠CDB=∠A+∠ABD=2∠C,
∴∠C+2∠C+2∠C=180°,
∴∠C=36°,
∴∠DBC=72°.
72°
A
B
C
D
2.如图,三角形ABC中,AC=BC,D是BC上的一点,连接 AD,DF平分∠ADC交∠ACB的外角∠ACE的平分线于F.
(1)求证:CF∥AB;
(2)若∠DAC=40°,求∠DFC的度数.
A
B
C
D
E
F
(1)证明:∵AC=BC,
∴∠ACE=∠ABC+∠CAB=2∠ABC,
∴∠ABC=∠CAB,
∵CF是∠ACE的平分线,∴∠ACE=2∠FCE,
∴2∠ABC=2∠FCE,∴∠ABC=∠FCE,
∴CF∥AB;
(2)∵CF是∠ACE的平分线,
∴∠ACE=2∠FCE=∠ADC+∠DAC,
∵DF平分∠ADC,∴∠ADC=2∠FDC,
∴2∠FCE=∠ADC+∠DAC=2∠FDC+∠DAC,
∴2∠FCE﹣2∠FDC=∠DAC,
∵∠DFC=∠FCE﹣∠FDC,
∴2∠DFC=2∠FCE﹣2∠FDC=∠DAC=40°,
∴∠DFC=20°.
3.如图所示,在Rt△ABC中,∠C=90°,BE是∠ABC的平分线,ED是AB边的垂直平分线.求∠A的度数.
解:∵BE 是∠ABC的平分线,
∴∠CBE=∠ABE,
∵ED是AB边的垂直平分线,
∴BE=AE,
∴∠EBD=∠EAB,
设∠A=x°,
则∠CBE=∠EBD=∠A=x°,
∵∠C=90°,
∴∠A+∠CBA=90°,
即3x=90°,
解得x=30°,
∴∠A=30°.
A
B
C
D
E
A
C
B
D
E
4. 求证:等腰三角形底边上的中点到两腰的距离相等.
F
已知:如图,在△ABC中,AB=AC,D为BC的中 点,DE ⊥ AB,DF ⊥AC.
求证: DE=DF.
证明: ∵AB=AC,∴∠ABC=∠ACB,
∵ D为BC的中 点, ∴BD=CD.
∵ DE ⊥ AB,DF ⊥AC,
∴∠DEB=∠DFC,
∴△EDB≌△FDC(AAS),
∴DE=CF.
课堂小结
等腰三角形的性质应用
等边对等角
三线合一
文字证明题
1.根据题意写出已知和求证;
2.画出符合题意的图形;
3.根据已知、求证写出证明过程.
求角的度数
