2021-2022学年广西贵港市桂平市八年级(下)期末数学试卷(word解析版)
文档属性
| 名称 | 2021-2022学年广西贵港市桂平市八年级(下)期末数学试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 333.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-06 23:28:11 | ||
图片预览



文档简介
2021-2022学年广西贵港市桂平市八年级(下)期末数学试卷
一、选择题(12小题,每小题3分,共36分,每小题给出的4个选项中只有一个是正确的)
1.(3分)在平面直角坐标系中,点P(2,﹣3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(3分)下列各组线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6 C.5,12,13 D.4,6,7
3.(3分)若一个多边形的每个外角都等于60°,则它的内角和等于( )
A.180° B.720° C.1080° D.540°
4.(3分)下列条件中,不能判定 ABCD为矩形的是( )
A.∠A=∠C B.∠A=∠B C.AC=BD D.AB⊥BC
5.(3分)班级共有40名学生,在一次体育抽测中有4人不合格,那么不合格人数的频率为( )
A.0.01 B.0.1 C.0.2 D.0.5
6.(3分)下列说法中,错误的是( )
A.角平分线上的点到角两边的距离相等
B.正方形的对角线互相垂直平分
C.斜边和一锐角对应相等的两个直角三角形全等
D.如果两个三角形全等,那么这两个三角形一定成中心对称
7.(3分)在平面直角坐标系中,若点P(a﹣3,1)与点Q(2,b+1)关于x轴对称,则a+b的值是( )
A.1 B.2 C.3 D.4
8.(3分)已知一次函数y=(a+3)x+b+1的图象经过过一、二、四象限,那么a,b的取值范围是( )
A.a>﹣3,b>﹣1 B.a<﹣3,b<﹣1 C.a>﹣3,b<﹣1 D.a<﹣3,b>﹣1
9.(3分)如图,CD是△ABC的中线,∠ACB=90°,∠CDB=100°,则∠A等于( )
A.20° B.45° C.50° D.80°
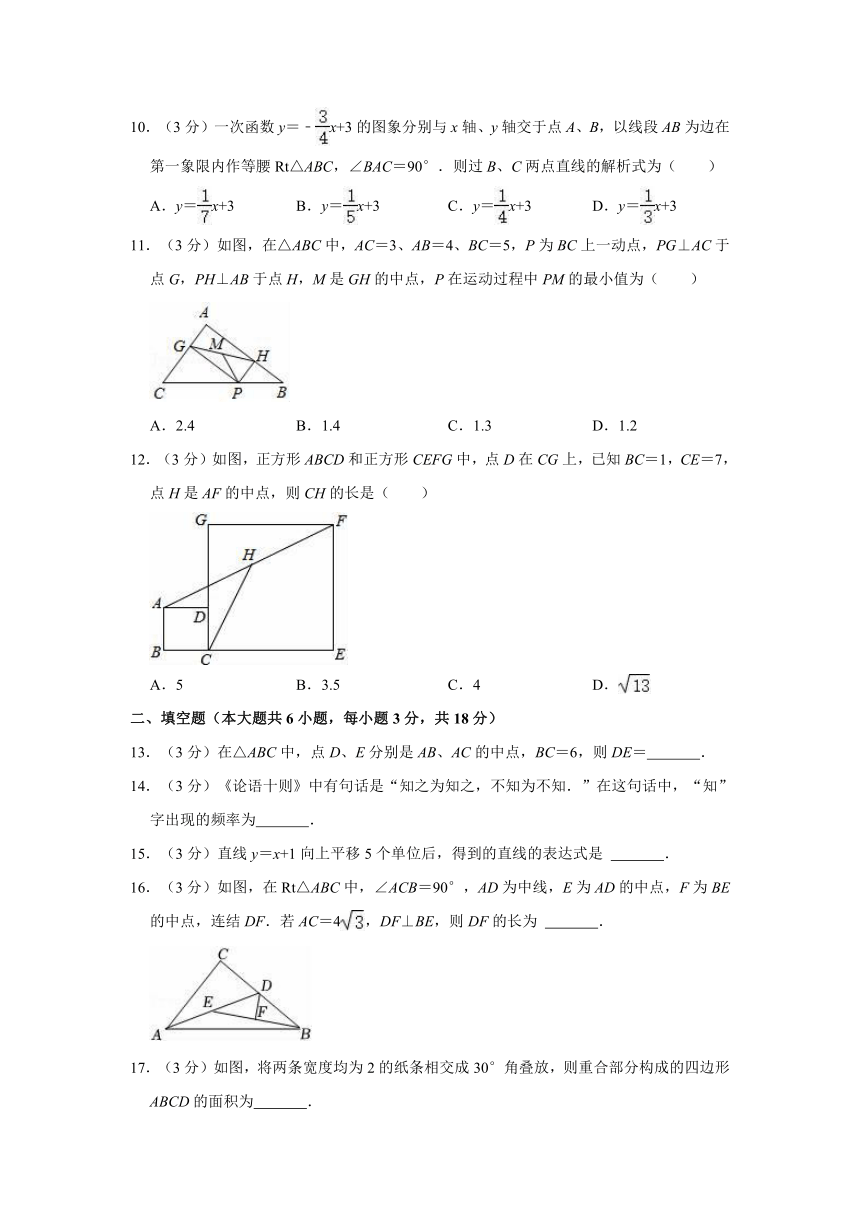
10.(3分)一次函数y=﹣x+3的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.则过B、C两点直线的解析式为( )
A.y=x+3 B.y=x+3 C.y=x+3 D.y=x+3
11.(3分)如图,在△ABC中,AC=3、AB=4、BC=5,P为BC上一动点,PG⊥AC于点G,PH⊥AB于点H,M是GH的中点,P在运动过程中PM的最小值为( )
A.2.4 B.1.4 C.1.3 D.1.2
12.(3分)如图,正方形ABCD和正方形CEFG中,点D在CG上,已知BC=1,CE=7,点H是AF的中点,则CH的长是( )
A.5 B.3.5 C.4 D.
二、填空题(本大题共6小题,每小题3分,共18分)
13.(3分)在△ABC中,点D、E分别是AB、AC的中点,BC=6,则DE= .
14.(3分)《论语十则》中有句话是“知之为知之,不知为不知.”在这句话中,“知”字出现的频率为 .
15.(3分)直线y=x+1向上平移5个单位后,得到的直线的表达式是 .
16.(3分)如图,在Rt△ABC中,∠ACB=90°,AD为中线,E为AD的中点,F为BE的中点,连结DF.若AC=4,DF⊥BE,则DF的长为 .
17.(3分)如图,将两条宽度均为2的纸条相交成30°角叠放,则重合部分构成的四边形ABCD的面积为 .
18.(3分)对于点P(a,b),点Q(c,d),如果a﹣b=c﹣d,那么点P与点Q就叫作等差点.例如:点P(4,2),点Q(﹣1,﹣3),因4﹣2=﹣1﹣(﹣3)=2,则点P与点Q就是等差点.如图在矩形GHMN中,点H(2,3),点N(﹣2,﹣3),MN⊥y轴,HM⊥x轴,点P是直线y=x+b上的任意一点(点P不在矩形的边上),若矩形GHMN的边上存在两个点与点P是等差点,则b的取值范围为 .
三、解答题(本大题共8小题,共66分解答应写出文字说明、证明过程或演算步骤)
19.(6分)设一次函数y=kx+b(k≠0)的图象经过A(1,3)、B(0,﹣2)两点,求此函数的解析式.
20.(6分)已知△ABC的三边长a、b、c满足|a﹣4|+(2b﹣12)2+=0,试判断△ABC的形状,并说明理由.
21.(8分)如图,BD是 ABCD的一条对角线,过A、C两点做AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、CF于M、N.
(1)求证:四边形CMAN是平行四边形;
(2)已知DM=2,AN=3,求AB的长.
22.(8分)某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力抽样调查,并将调查的数据进行统计整理,绘制出如图的频数分布表和频数分布直方图.
视力 频数/人 频率
4.0≤x<4.3 20 0.1
4.3≤x<4.6 40 0.2
4.6≤x<4.9 80 0.4
4.9≤x<5.2 a 0.25
5.2≤x<5.5 10 b
(1)在频数分布表中,则a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比.
23.(8分)某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由.
24.(8分)已知:如图,边长为4的菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.
(1)求证:四边形ABCD是正方形.
(2)E是OB上一点,BE=1,且DH⊥CE,垂足为H,DH与OC相交于点F,求线段OF的长.
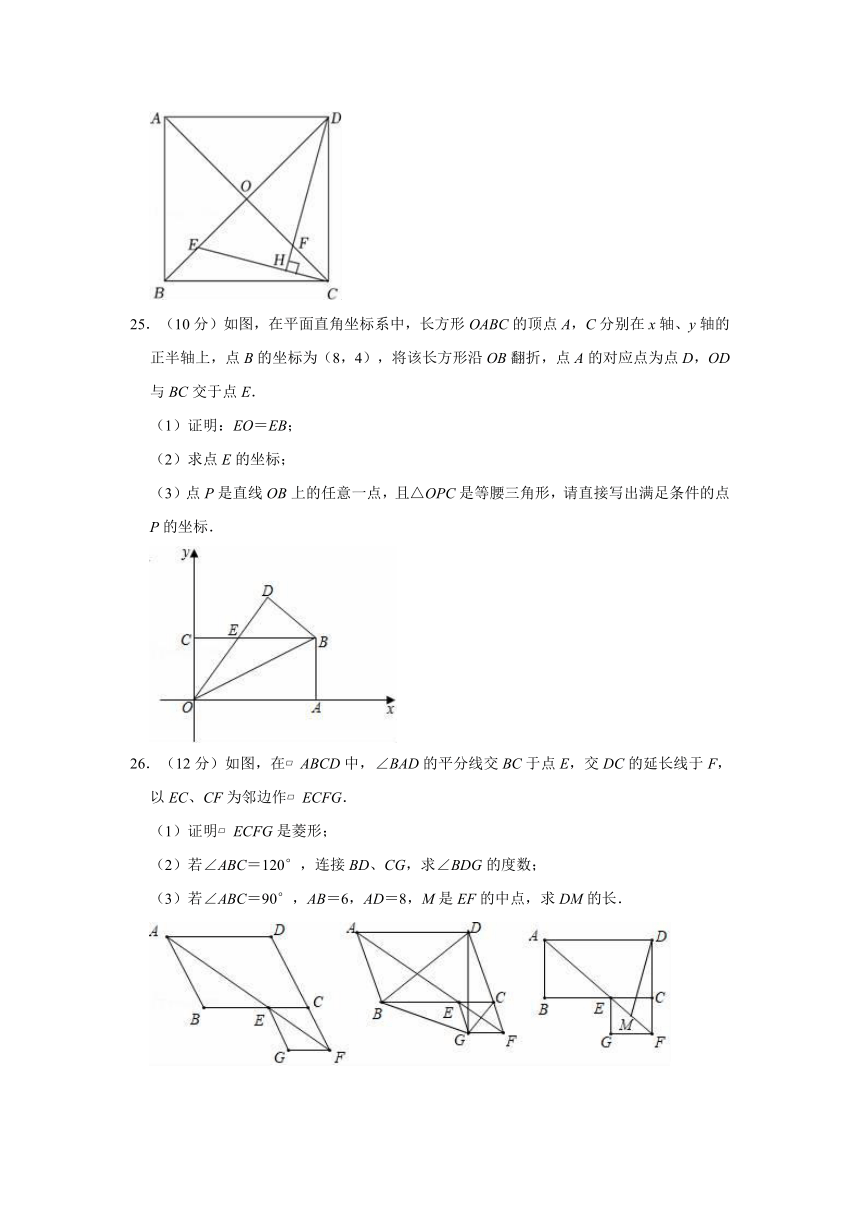
25.(10分)如图,在平面直角坐标系中,长方形OABC的顶点A,C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
(1)证明:EO=EB;
(2)求点E的坐标;
(3)点P是直线OB上的任意一点,且△OPC是等腰三角形,请直接写出满足条件的点P的坐标.
26.(12分)如图,在 ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作 ECFG.
(1)证明 ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
2021-2022学年广西贵港市桂平市八年级(下)期末数学试卷
参考答案与试题解析
一、选择题(12小题,每小题3分,共36分,每小题给出的4个选项中只有一个是正确的)
1.【分析】根据各象限内点的坐标特征解答.
【解答】解:点P(2,﹣3)在第四象限.
故选:D.
【点评】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
2.【分析】判断是否为直角三角形,只要验证两小边的平方和等于最长边的平方即可.
【解答】解:A、22+32=13≠42,故A选项构成不是直角三角形;
B、32+42=25≠62,故B选项构成不是直角三角形;
C、52+122=169=132,故C选项构成是直角三角形;
D、42+62=52≠72,故D选项构成不是直角三角形.
故选:C.
【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
3.【分析】由一个多边形的每个外角都等于60°,根据n边形的外角和为360°计算出多边形的边数n,然后根据n边形的内角和定理计算即可.
【解答】解:设多边形的边数为n,
∵多边形的每个外角都等于60°,
∴n=360°÷60°=6,
∴这个多边形的内角和=(6﹣2)×180°=720°.
故选:B.
【点评】本题考查了n边形的内角和定理:n边形的内角和=(n﹣2) 180°;也考查了n边形的外角和为360°.
4.【分析】由矩形的判定方法分别对各个选项进行判断,即可得出结论.
【解答】解:A、在 ABCD,若∠A=∠C,
则四边形ABCD还是平行四边形;故选项A符合题意;
B、在 ABCD中,AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴ ABCD是矩形,故选项B不符合题意;
C、在 ABCD中,AC=BD,
则 ABCD是矩形;故选项C不符合题意;
D、在 ABCD中,AB⊥BC,
∴∠ABC=90°,
∴ ABCD是矩形,故选项D不符合题意;
故选:A.
【点评】本题主要考查了矩形的判定以及平行四边形的性质;熟练掌握矩形的判定方法是解题的关键.
5.【分析】根据频率的计算公式求得不合格人数的频率即可.
【解答】解:∵班级共有40名学生,在一次体育抽测中有4人不合格,
∴不合格人数的频率是=0.1.
故选:B.
【点评】本题主要考查了频率与概率,解题的关键是明确频率是指每个对象出现的次数与总次数的比值(或者百分比).
6.【分析】根据角平分线的性质即可判断选项A;根据正方形的性质即可判断选项B;根据全等三角形的判定即可判断选项C;根据中心对称的性质和全等三角形的性质即可判断选项D.
【解答】解:A.角平分线上的点到角两边的距离相等,正确,故本选项不符合题意;
B.正方形的对角线互相平分,垂直且相等,正确,故本选项不符合题意;
C.斜边和一锐角对应相等(还有直角相等),符合两直角三角形的全等的判定定理AAS,能推出两直角三角形全等,正确,故本选项不符合题意;
D.如图:
两三角形全等,但是两三角形不关于一点成中心对称,错误,故本选项符合题意;
故选:D.
【点评】本题考查了全等三角形的判定和性质,中心对称的性质,正方形的性质,角平分线的性质等知识点,能熟记全等三角形的判定和性质、中心对称的性质、正方形的性质、角平分线的性质是解此题的关键.
7.【分析】直接利用关于x轴对称点的性质:横坐标不变,纵坐标互为相反数,即可得出a,b的值,进而得出答案.
【解答】解:∵点P(a﹣3,1)与点Q(2,b+1)关于x轴对称,
∴a﹣3=2,b+1=﹣1,
∴a=5,b=﹣2,
则a+b=5﹣2=3.
故选:C.
【点评】此题主要考查了关于x轴对称点的性质,正确记忆关于x轴对称点的符号关系是解题关键.
8.【分析】根据一次函数图象经过第一、二、四象限,则a+3<0,b+1>0,即可求解.
【解答】解:一次函数y=(a+3)x+b+1的图象经过过一、二、四象限,
故a+3<0,b+1>0,
∴a<﹣3,b>﹣1,
故选:D.
【点评】本题考查的是一次函数的图象与系数的关系,即一次函数y=kx+b(k≠0)中,当k<0,b>0时函数的图象在一、二、四象限.
9.【分析】根据直角三角形斜边上的中线性质求出CD=AB,求出CD=AD,根据等腰三角形的性质求出∠A=∠ACD,根据三角形的外角性质求出∠CDB=∠A+∠ACD,再求出答案即可.
【解答】解:∵CD是△ABC的中线,∠ACB=90°,
∴CD=AB,AD=AB,
∴CD=AD,
∴∠A=∠ACD,
∵∠CDB=∠A+∠ACD,∠CDB=100°,
∴100°=2∠A,
即∠A=50°,
故选:C.
【点评】本题考查了直角三角形斜边上的中线的性质,三角形外角性质和等腰三角形的性质等知识点,能熟记直角三角形斜边上的中线性质是解此题的关键,注意:直角三角形斜边上的中线等于斜边的一半.
10.【分析】先根据一次函数的解析式求出A、B两点的坐标,再作CD⊥x轴于点D,由全等三角形的判定定理可得出△ABO≌△CAD,由全等三角形的性质可知OA=CD,故可得出C点坐标,再用待定系数法即可求出直线BC的解析式.
【解答】解:∵一次函数y=﹣x+3中,
令x=0得:y=3;令y=0,解得x=4,
∴B的坐标是(0,3),A的坐标是(4,0),
如图,作CD⊥x轴于点D,
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO,
在△ABO与△CAD中,
,
∴△ABO≌△CAD(AAS),
∴OB=AD=3,OA=CD=4,OD=OA+AD=7,
则C的坐标是(7,4),
设直线BC的解析式是y=kx+b,
根据题意得:,
解得:,
∴直线BC的解析式是y=x+3
故选:A.
【点评】本题考查的是待定系数法求一次函数的解析式、全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.
11.【分析】先由勾股定理的逆定理证出△ABC是直角三角形,∠BAC=90°,再证四边形AGPH为矩形,得AP与GH互相平分且相等,则M是AP的中点,当AP⊥BC时,AP最小,然后由三角形面积求出AP的长,即可求解.
【解答】解:连接PA,如图所示:
∵AC=3、AB=4、BC=5,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∵PG⊥AC于点G,PH⊥AB于点H,
∴∠PGA=∠PHA=90°,
∴四边形AGPH为矩形,
∴AP与GH互相平分且相等,
∵M是GH的中点,
∴M是AP的中点,
当AP⊥BC时,AP最小,
此时,△ABC的面积BC×AP=AC×AB,
则AP===2.4,
∴PM=AP=1.2,
即PM的最小值为1.2,
故选:D.
【点评】此题考查了矩形的判定与性质、勾股定理的逆定理以及三角形面积等知识;熟练掌握矩形的判定与性质,求出当AP⊥AB时AP的长是解题的关键.
12.【分析】根据正方形的性质求出AB=BC=1,CE=EF=7,∠E=90°,延长AD交EF于M,连接AC、CF,求出AM=8,FM=6,∠AMF=90°,根据正方形性质求出∠ACF=90°,根据直角三角形斜边上的中线性质求出CH=AF,根据勾股定理求出AF即可.
【解答】解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=7,
∴AB=BC=1,CE=EF=7,∠E=90°,
延长AD交EF于M,连接AC、CF,
则AM=BC+CE=1+7=8,FM=EF﹣AB=7﹣1=6,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
∵H为AF的中点,
∴CH=AF,
在Rt△AMF中,由勾股定理得:AF===10,
∴CH=5,
故选:A.
【点评】本题考查了勾股定理,正方形的性质,直角三角形斜边上的中线的应用,解此题的关键是能正确作出辅助线,并求出AF的长和得出CH=AF,有一定的难度.
二、填空题(本大题共6小题,每小题3分,共18分)
13.【分析】根据三角形的中位线定理得出DE=BC,代入求出即可.
【解答】解:如图,
∵在△ABC中,点D、E分别是AB、AC的中点,
∴DE=BC,
∵BC=6,
∴DE=3,
故答案为:3.
【点评】本题考查了三角形的中位线性质,能根据三角形的中位线性质得出DE=BC是解此题的关键.
14.【分析】用“知”字出现的次数除以字的总个数即可得.
【解答】解:∵这句话共有10个字,其中“知”字出现4次,
∴在这句话中,“知”字出现的频率为=,
故答案为:.
【点评】本题主要考查频数与频率,一般称落在不同小组中的数据个数为该组的频数,频数与数据总数的比值为频率.频率反映了各组频数的大小在总数中所占的分量.
15.【分析】直接根据上加下减的平移规律求解即可.
【解答】解:直线y=x+1向上平移5个单位后,得到的直线的解析式是y=x+1+5,即y=x+6.
故答案为:y=x+6.
【点评】本题考查了一次函数图象与几何变换,熟记直线解析式平移的规律:“上加下减,左加右减”是解题的关键.
16.【分析】连接CE,由中位线的性质可得CE=2DF,DF∥CE,再证△DEF≌△DBF(SAS),进而可证CD=ED,然后证CD=AD,AD=4DF,利用勾股定理求出AD的长,即可解决问题.
【解答】解:如图,连接CE,
∵AD是BC边上的中线,F点为BE的中点,
∴DF为△BCE的中位线,
∴CE=2DF,DF∥CE,
∴∠BDF=∠DCE,∠EDF=∠DEC,
∵DF⊥BE,
∴∠DFE=∠DFB=90°,
在△DEF和△DBF中,
,
∴△DEF≌△DBF(SAS),
∴∠EDF=∠BDF,
∴∠DEC=∠DCE,
∴CD=ED,
∵E为AD的中点,∠ACB=90°,
∴CE=ED=CD=AD,
∴AD=4DF,
∵AC=4,
在Rt△ACD中,由勾股定理得:CD2+AC2=AD2,
即(AD)2+(4)2=AD2,
解得:AD=8(负值已舍去),
∴DF=2.
故答案为:2.
【点评】本题考查了勾股定理,全等三角形的判定与性质,等腰三角形的判定与性质,三角形中位线定理等知识,熟练掌握勾股定理,证出AD=4DF是解题的关键.
17.【分析】先可判断重叠部分为平行四边形,再由平行四边形的面积可得邻边相等,则重叠部分为菱形,然后由含30°角的直角三角形的性质求出BC=AB=4,最后根据平行四边形的面积公式求得即可.
【解答】解:过点A作AE⊥BC于E,AF⊥CD于F,如图所示:
∵两条纸条宽度相同,
∴AE=AF,
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,∠ABC=30°,
∵S ABCD=BC AE=CD AF,
又∵AE=AF,
∴BC=CD,
∴四边形ABCD是菱形,
∴AB=BC,
在Rt△AEB中,∠AEB=90°,∠ABC=30°,AE=2,
∴BC=AB=2AE=4,
∴四边形ABCD的面积=BC AE=4×2=8,
故答案为:8.
【点评】本题考查了菱形的判定与性质、平行四边形的判定与性质、含30°角的直角三角形的性质等知识,证得四边形ABCD为菱形是解题的关键.
18.【分析】由题意,G(﹣2,3),M(2,﹣3),根据等差点的定义可知,当直线y=x+b与矩形MNGH有两个交点时,矩形GHMN的边上存在两个点与点P是等差点,求出直线经过点G或M时的b的值即可判断.
【解答】解:由题意,G(﹣2,3),M(2,﹣3),
根据等差点的定义可知,当直线y=x+b与矩形MNGH有两个交点时,矩形GHMN的边上存在两个点与点P是等差点,
当直线y=x+b经过点G(﹣2,3)时,b=5,
当直线y=x+b经过点M(2,﹣3)时,b=﹣5,
∴满足条件的b的范围为:﹣5<b<5.
故答案为﹣5<b<5
【点评】本题考查一次函数图象上点的特征、矩形的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考填空题中的压轴题.
三、解答题(本大题共8小题,共66分解答应写出文字说明、证明过程或演算步骤)
19.【分析】直接把A点和B点坐标代入y=kx+b得到关于k、b的方程组,然后解方程组即可.
【解答】解:把A(1,3)、B(0,﹣2)代入y=kx+b得,解得,
所以此函数解析式为y=5x﹣2.
【点评】本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.
20.【分析】根据非负数的性质解得各边的长,再根据勾股定理的逆定理判定是否直角三角形.
【解答】解:△ABC为直角三角形,理由如下:
由题意得a﹣4=0,2b﹣12=0,10﹣c=0,
所以a=8,b=6,c=10,
因为82+62=102,
所以a2+b2=c2,
∴△ABC为直角三角形.
【点评】此题考查了勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.也考查了非负数的性质,解本题的关键是求出a,b,c的值.
21.【分析】(1)先证AM∥CN,再由平行四边形的性质得CM∥AN,然后由平行四边形的判定即可得出结论;
(2)根据平行四边形的性质解答即可.
【解答】(1)证明:∵AE⊥BD,CF⊥BD,
∴AM∥CN,
∵四边形ABCD是平行四边形,
∴CM∥AN,
∴四边形CMAN是平行四边形;
(2)解:∵四边形ABCD是平行四边形,
∴DC=AB,
∵四边形CMAN是平行四边形,
∴CM=AN,
∴CD﹣CM=AB﹣AN,
即DM=BN=2,
∴AB=AN+DM=3+2=5.
【点评】本题考查平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解题的关键.
22.【分析】(1)根据频数分布表中的数据,可以计算出本次调查的人数,然后即可计算出a和b的值;
(2)根据(1)中a的值,可以将频数分布直方图补充完整;
(3)根据频数分布表中的数据,可以计算出视力正常的人数占被调查人数的百分比.
【解答】解:(1)本次调查的人数为:20÷0.1=200,
a=200×0.25=50,b=10÷200=0.05,
故答案为:50,0.05;
(2)由(1)知,a=50,
补全的频数分布直方图如右图所示;
(3)(0.4+0.25+0.05)×100%=70%,
答:视力正常的人数占被调查人数的百分比是70%.
【点评】本题考查频数分布直方图、频数分布表,解答本题的关键是明确题意,利用数形结合的思想解答.
23.【分析】(1)根据甲,乙两种销售方案,分别得出两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,即单价×质量,列出即可;
(2)根据分析9x与8x+5000的大小关系,得出不等式的解集可以得出购买方案付款的多少问题.
【解答】解:(1)甲方案:每千克9元,由基地送货上门,
根据题意得:y=9x;x≥3000,
乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元,
根据题意得:y=8x+5000;x≥3000.
(2)根据题意可得:当9x=8x+5000时,
x=5000,
当购买5000千克时两种购买方案付款相同,
当大于5000千克时,9x>8x+5000,
∴甲方案付款多,乙付款少,
当小于5000千克时,9x<8x+5000,
∴甲方案付款少,乙付款多.
【点评】此题主要考查了一次函数的应用,得出两函数的解析式利用不等式即可得出付费的多少.
24.【分析】(1)由菱形的性质得出AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,得出∠BAD+∠ABC=180°,证出∠BAD=∠ABC,求出∠BAD=90°,即可得出结论;
(2)由正方形的性质得出AC⊥BD,AC=BD,CO=AC,DO=BD,得出∠COB=∠DOC=90°,CO=DO,证出∠ECO=∠EDH,证明△ECO≌△FDO(ASA),即可得出结论.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,
∴∠BAD+∠ABC=180°,
∵∠CAD=∠DBC,
∴∠BAD=∠ABC,
∴2∠BAD=180°,
∴∠BAD=90°,
∴四边形ABCD是正方形;
(2)解:∵四边形ABCD是正方形,AB=BC=4,
∴AC⊥BD,AC=BD=4,
∴OB=CO=AC=2,DO=BD=2,
∴∠COB=∠DOC=90°,CO=DO,
∵DH⊥CE,垂足为H,
∴∠DHE=90°,∠EDH+∠DEH=90°,
∵∠ECO+∠DEH=90°,
∴∠ECO=∠EDH,
在△ECO和△FDO中,
,
∴△ECO≌△FDO(ASA),
∴OE=OF.
∵BE=1,
∴OE=OF=OB﹣BE=2﹣1.
【点评】本题考查了正方形的判定与性质、菱形的性质,全等三角形的判定与性质等知识;熟练掌握正方形的判定与性质是解题关键.
25.【分析】(1)由折叠得到∠DOB=∠AOB,再由BC∥OA得到∠OBC=∠AOB,即∠OBC=∠DOB,即可得出结论;
(2)由(1)得到EO=EB设OE=x则CE=8﹣x,再用勾股定理建立方程16+(8﹣x)2=x2,求出x即可;
(3)设出点P坐标,分三种情况,根据等腰三角形的性质即可求解.
【解答】(1)证明:∵将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
∴∠DOB=∠AOB,
∵四边形OABC是长方形,
∴BC∥OA,
∴∠OBC=∠AOB,
∴∠OBC=∠DOB,
∴EO=EB;
(2)解:由(1)得,EO=EB,
∵长方形OABC的顶点A,C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),
设OE=BE=x,则CE=8﹣x,
在Rt△OCE中,OC=4,根据勾股定理得,OC2+CE2=OE2,
∴16+(8﹣x)2=x2,
∴x=5,
∴BE=5,
∴CE=3,
∴E(3,4);
(3)解:点B的坐标为(8,4),
∴直线OB解析式为y=x,
∵点P是直线OB上的任意一点,
∴设P(a, a),
∵O(0,0),C(0,4),
∴OC=4,PO2=a2+(a)2=a2,PC2=a2+(4﹣a)2,
∵△OPC是等腰三角形,
①当PO=PC时,PO2=PC2,
∴a2=a2+(4﹣a)2,
∴a=4,
∴P(4,2);
②当PO=OC时,PO2=OC2,
∴a2=16,
∴a=±,
∴P(,)或P(﹣,﹣);
③当PC=OC时,PC2=OC2,
∴a2+(4﹣a)2=16,
∴a=0(舍)或a=,
∴P(,);
∴满足条件的点P的坐标为(4,2)或(,)或P(﹣,﹣)或(,).
【点评】此题是四边形综合题,主要考查了矩形的性质,折叠的性质,勾股定理,等腰三角形的性质,解本题的关键求出点E的坐标,学会用分类讨论的思想思考问题.
26.【分析】(1)平行四边形的性质可得AD∥BC,AB∥CD,再根据平行线的性质证明∠CEF=∠CFE,根据等角对等边可得CE=CF,再有条件四边形ECFG是平行四边形,可得四边形ECFG为菱形,即可解决问题;
(2)先判断出∠BEG=120°=∠DCG,再判断出AB=BE,进而得出BE=CD,即可判断出△BEG≌△DCG(SAS),再判断出∠CGE=60°,进而得出△BDG是等边三角形,即可得出结论;
(3)首先证明四边形ECFG为正方形,再证明△BME≌△DMC可得DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到△BDM是等腰直角三角形,由等腰直角三角形的性质即可得到结论.
【解答】解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图2中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DM=BD=5.
【点评】此题主要考查平行四边形的判定方法,全等三角形的判定与性质,等边三角形的判定与性质,菱形的判定与性质等知识点,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.
一、选择题(12小题,每小题3分,共36分,每小题给出的4个选项中只有一个是正确的)
1.(3分)在平面直角坐标系中,点P(2,﹣3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(3分)下列各组线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6 C.5,12,13 D.4,6,7
3.(3分)若一个多边形的每个外角都等于60°,则它的内角和等于( )
A.180° B.720° C.1080° D.540°
4.(3分)下列条件中,不能判定 ABCD为矩形的是( )
A.∠A=∠C B.∠A=∠B C.AC=BD D.AB⊥BC
5.(3分)班级共有40名学生,在一次体育抽测中有4人不合格,那么不合格人数的频率为( )
A.0.01 B.0.1 C.0.2 D.0.5
6.(3分)下列说法中,错误的是( )
A.角平分线上的点到角两边的距离相等
B.正方形的对角线互相垂直平分
C.斜边和一锐角对应相等的两个直角三角形全等
D.如果两个三角形全等,那么这两个三角形一定成中心对称
7.(3分)在平面直角坐标系中,若点P(a﹣3,1)与点Q(2,b+1)关于x轴对称,则a+b的值是( )
A.1 B.2 C.3 D.4
8.(3分)已知一次函数y=(a+3)x+b+1的图象经过过一、二、四象限,那么a,b的取值范围是( )
A.a>﹣3,b>﹣1 B.a<﹣3,b<﹣1 C.a>﹣3,b<﹣1 D.a<﹣3,b>﹣1
9.(3分)如图,CD是△ABC的中线,∠ACB=90°,∠CDB=100°,则∠A等于( )
A.20° B.45° C.50° D.80°
10.(3分)一次函数y=﹣x+3的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.则过B、C两点直线的解析式为( )
A.y=x+3 B.y=x+3 C.y=x+3 D.y=x+3
11.(3分)如图,在△ABC中,AC=3、AB=4、BC=5,P为BC上一动点,PG⊥AC于点G,PH⊥AB于点H,M是GH的中点,P在运动过程中PM的最小值为( )
A.2.4 B.1.4 C.1.3 D.1.2
12.(3分)如图,正方形ABCD和正方形CEFG中,点D在CG上,已知BC=1,CE=7,点H是AF的中点,则CH的长是( )
A.5 B.3.5 C.4 D.
二、填空题(本大题共6小题,每小题3分,共18分)
13.(3分)在△ABC中,点D、E分别是AB、AC的中点,BC=6,则DE= .
14.(3分)《论语十则》中有句话是“知之为知之,不知为不知.”在这句话中,“知”字出现的频率为 .
15.(3分)直线y=x+1向上平移5个单位后,得到的直线的表达式是 .
16.(3分)如图,在Rt△ABC中,∠ACB=90°,AD为中线,E为AD的中点,F为BE的中点,连结DF.若AC=4,DF⊥BE,则DF的长为 .
17.(3分)如图,将两条宽度均为2的纸条相交成30°角叠放,则重合部分构成的四边形ABCD的面积为 .
18.(3分)对于点P(a,b),点Q(c,d),如果a﹣b=c﹣d,那么点P与点Q就叫作等差点.例如:点P(4,2),点Q(﹣1,﹣3),因4﹣2=﹣1﹣(﹣3)=2,则点P与点Q就是等差点.如图在矩形GHMN中,点H(2,3),点N(﹣2,﹣3),MN⊥y轴,HM⊥x轴,点P是直线y=x+b上的任意一点(点P不在矩形的边上),若矩形GHMN的边上存在两个点与点P是等差点,则b的取值范围为 .
三、解答题(本大题共8小题,共66分解答应写出文字说明、证明过程或演算步骤)
19.(6分)设一次函数y=kx+b(k≠0)的图象经过A(1,3)、B(0,﹣2)两点,求此函数的解析式.
20.(6分)已知△ABC的三边长a、b、c满足|a﹣4|+(2b﹣12)2+=0,试判断△ABC的形状,并说明理由.
21.(8分)如图,BD是 ABCD的一条对角线,过A、C两点做AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、CF于M、N.
(1)求证:四边形CMAN是平行四边形;
(2)已知DM=2,AN=3,求AB的长.
22.(8分)某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力抽样调查,并将调查的数据进行统计整理,绘制出如图的频数分布表和频数分布直方图.
视力 频数/人 频率
4.0≤x<4.3 20 0.1
4.3≤x<4.6 40 0.2
4.6≤x<4.9 80 0.4
4.9≤x<5.2 a 0.25
5.2≤x<5.5 10 b
(1)在频数分布表中,则a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比.
23.(8分)某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由.
24.(8分)已知:如图,边长为4的菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.
(1)求证:四边形ABCD是正方形.
(2)E是OB上一点,BE=1,且DH⊥CE,垂足为H,DH与OC相交于点F,求线段OF的长.
25.(10分)如图,在平面直角坐标系中,长方形OABC的顶点A,C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
(1)证明:EO=EB;
(2)求点E的坐标;
(3)点P是直线OB上的任意一点,且△OPC是等腰三角形,请直接写出满足条件的点P的坐标.
26.(12分)如图,在 ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作 ECFG.
(1)证明 ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
2021-2022学年广西贵港市桂平市八年级(下)期末数学试卷
参考答案与试题解析
一、选择题(12小题,每小题3分,共36分,每小题给出的4个选项中只有一个是正确的)
1.【分析】根据各象限内点的坐标特征解答.
【解答】解:点P(2,﹣3)在第四象限.
故选:D.
【点评】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
2.【分析】判断是否为直角三角形,只要验证两小边的平方和等于最长边的平方即可.
【解答】解:A、22+32=13≠42,故A选项构成不是直角三角形;
B、32+42=25≠62,故B选项构成不是直角三角形;
C、52+122=169=132,故C选项构成是直角三角形;
D、42+62=52≠72,故D选项构成不是直角三角形.
故选:C.
【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
3.【分析】由一个多边形的每个外角都等于60°,根据n边形的外角和为360°计算出多边形的边数n,然后根据n边形的内角和定理计算即可.
【解答】解:设多边形的边数为n,
∵多边形的每个外角都等于60°,
∴n=360°÷60°=6,
∴这个多边形的内角和=(6﹣2)×180°=720°.
故选:B.
【点评】本题考查了n边形的内角和定理:n边形的内角和=(n﹣2) 180°;也考查了n边形的外角和为360°.
4.【分析】由矩形的判定方法分别对各个选项进行判断,即可得出结论.
【解答】解:A、在 ABCD,若∠A=∠C,
则四边形ABCD还是平行四边形;故选项A符合题意;
B、在 ABCD中,AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴ ABCD是矩形,故选项B不符合题意;
C、在 ABCD中,AC=BD,
则 ABCD是矩形;故选项C不符合题意;
D、在 ABCD中,AB⊥BC,
∴∠ABC=90°,
∴ ABCD是矩形,故选项D不符合题意;
故选:A.
【点评】本题主要考查了矩形的判定以及平行四边形的性质;熟练掌握矩形的判定方法是解题的关键.
5.【分析】根据频率的计算公式求得不合格人数的频率即可.
【解答】解:∵班级共有40名学生,在一次体育抽测中有4人不合格,
∴不合格人数的频率是=0.1.
故选:B.
【点评】本题主要考查了频率与概率,解题的关键是明确频率是指每个对象出现的次数与总次数的比值(或者百分比).
6.【分析】根据角平分线的性质即可判断选项A;根据正方形的性质即可判断选项B;根据全等三角形的判定即可判断选项C;根据中心对称的性质和全等三角形的性质即可判断选项D.
【解答】解:A.角平分线上的点到角两边的距离相等,正确,故本选项不符合题意;
B.正方形的对角线互相平分,垂直且相等,正确,故本选项不符合题意;
C.斜边和一锐角对应相等(还有直角相等),符合两直角三角形的全等的判定定理AAS,能推出两直角三角形全等,正确,故本选项不符合题意;
D.如图:
两三角形全等,但是两三角形不关于一点成中心对称,错误,故本选项符合题意;
故选:D.
【点评】本题考查了全等三角形的判定和性质,中心对称的性质,正方形的性质,角平分线的性质等知识点,能熟记全等三角形的判定和性质、中心对称的性质、正方形的性质、角平分线的性质是解此题的关键.
7.【分析】直接利用关于x轴对称点的性质:横坐标不变,纵坐标互为相反数,即可得出a,b的值,进而得出答案.
【解答】解:∵点P(a﹣3,1)与点Q(2,b+1)关于x轴对称,
∴a﹣3=2,b+1=﹣1,
∴a=5,b=﹣2,
则a+b=5﹣2=3.
故选:C.
【点评】此题主要考查了关于x轴对称点的性质,正确记忆关于x轴对称点的符号关系是解题关键.
8.【分析】根据一次函数图象经过第一、二、四象限,则a+3<0,b+1>0,即可求解.
【解答】解:一次函数y=(a+3)x+b+1的图象经过过一、二、四象限,
故a+3<0,b+1>0,
∴a<﹣3,b>﹣1,
故选:D.
【点评】本题考查的是一次函数的图象与系数的关系,即一次函数y=kx+b(k≠0)中,当k<0,b>0时函数的图象在一、二、四象限.
9.【分析】根据直角三角形斜边上的中线性质求出CD=AB,求出CD=AD,根据等腰三角形的性质求出∠A=∠ACD,根据三角形的外角性质求出∠CDB=∠A+∠ACD,再求出答案即可.
【解答】解:∵CD是△ABC的中线,∠ACB=90°,
∴CD=AB,AD=AB,
∴CD=AD,
∴∠A=∠ACD,
∵∠CDB=∠A+∠ACD,∠CDB=100°,
∴100°=2∠A,
即∠A=50°,
故选:C.
【点评】本题考查了直角三角形斜边上的中线的性质,三角形外角性质和等腰三角形的性质等知识点,能熟记直角三角形斜边上的中线性质是解此题的关键,注意:直角三角形斜边上的中线等于斜边的一半.
10.【分析】先根据一次函数的解析式求出A、B两点的坐标,再作CD⊥x轴于点D,由全等三角形的判定定理可得出△ABO≌△CAD,由全等三角形的性质可知OA=CD,故可得出C点坐标,再用待定系数法即可求出直线BC的解析式.
【解答】解:∵一次函数y=﹣x+3中,
令x=0得:y=3;令y=0,解得x=4,
∴B的坐标是(0,3),A的坐标是(4,0),
如图,作CD⊥x轴于点D,
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO,
在△ABO与△CAD中,
,
∴△ABO≌△CAD(AAS),
∴OB=AD=3,OA=CD=4,OD=OA+AD=7,
则C的坐标是(7,4),
设直线BC的解析式是y=kx+b,
根据题意得:,
解得:,
∴直线BC的解析式是y=x+3
故选:A.
【点评】本题考查的是待定系数法求一次函数的解析式、全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.
11.【分析】先由勾股定理的逆定理证出△ABC是直角三角形,∠BAC=90°,再证四边形AGPH为矩形,得AP与GH互相平分且相等,则M是AP的中点,当AP⊥BC时,AP最小,然后由三角形面积求出AP的长,即可求解.
【解答】解:连接PA,如图所示:
∵AC=3、AB=4、BC=5,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∵PG⊥AC于点G,PH⊥AB于点H,
∴∠PGA=∠PHA=90°,
∴四边形AGPH为矩形,
∴AP与GH互相平分且相等,
∵M是GH的中点,
∴M是AP的中点,
当AP⊥BC时,AP最小,
此时,△ABC的面积BC×AP=AC×AB,
则AP===2.4,
∴PM=AP=1.2,
即PM的最小值为1.2,
故选:D.
【点评】此题考查了矩形的判定与性质、勾股定理的逆定理以及三角形面积等知识;熟练掌握矩形的判定与性质,求出当AP⊥AB时AP的长是解题的关键.
12.【分析】根据正方形的性质求出AB=BC=1,CE=EF=7,∠E=90°,延长AD交EF于M,连接AC、CF,求出AM=8,FM=6,∠AMF=90°,根据正方形性质求出∠ACF=90°,根据直角三角形斜边上的中线性质求出CH=AF,根据勾股定理求出AF即可.
【解答】解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=7,
∴AB=BC=1,CE=EF=7,∠E=90°,
延长AD交EF于M,连接AC、CF,
则AM=BC+CE=1+7=8,FM=EF﹣AB=7﹣1=6,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
∵H为AF的中点,
∴CH=AF,
在Rt△AMF中,由勾股定理得:AF===10,
∴CH=5,
故选:A.
【点评】本题考查了勾股定理,正方形的性质,直角三角形斜边上的中线的应用,解此题的关键是能正确作出辅助线,并求出AF的长和得出CH=AF,有一定的难度.
二、填空题(本大题共6小题,每小题3分,共18分)
13.【分析】根据三角形的中位线定理得出DE=BC,代入求出即可.
【解答】解:如图,
∵在△ABC中,点D、E分别是AB、AC的中点,
∴DE=BC,
∵BC=6,
∴DE=3,
故答案为:3.
【点评】本题考查了三角形的中位线性质,能根据三角形的中位线性质得出DE=BC是解此题的关键.
14.【分析】用“知”字出现的次数除以字的总个数即可得.
【解答】解:∵这句话共有10个字,其中“知”字出现4次,
∴在这句话中,“知”字出现的频率为=,
故答案为:.
【点评】本题主要考查频数与频率,一般称落在不同小组中的数据个数为该组的频数,频数与数据总数的比值为频率.频率反映了各组频数的大小在总数中所占的分量.
15.【分析】直接根据上加下减的平移规律求解即可.
【解答】解:直线y=x+1向上平移5个单位后,得到的直线的解析式是y=x+1+5,即y=x+6.
故答案为:y=x+6.
【点评】本题考查了一次函数图象与几何变换,熟记直线解析式平移的规律:“上加下减,左加右减”是解题的关键.
16.【分析】连接CE,由中位线的性质可得CE=2DF,DF∥CE,再证△DEF≌△DBF(SAS),进而可证CD=ED,然后证CD=AD,AD=4DF,利用勾股定理求出AD的长,即可解决问题.
【解答】解:如图,连接CE,
∵AD是BC边上的中线,F点为BE的中点,
∴DF为△BCE的中位线,
∴CE=2DF,DF∥CE,
∴∠BDF=∠DCE,∠EDF=∠DEC,
∵DF⊥BE,
∴∠DFE=∠DFB=90°,
在△DEF和△DBF中,
,
∴△DEF≌△DBF(SAS),
∴∠EDF=∠BDF,
∴∠DEC=∠DCE,
∴CD=ED,
∵E为AD的中点,∠ACB=90°,
∴CE=ED=CD=AD,
∴AD=4DF,
∵AC=4,
在Rt△ACD中,由勾股定理得:CD2+AC2=AD2,
即(AD)2+(4)2=AD2,
解得:AD=8(负值已舍去),
∴DF=2.
故答案为:2.
【点评】本题考查了勾股定理,全等三角形的判定与性质,等腰三角形的判定与性质,三角形中位线定理等知识,熟练掌握勾股定理,证出AD=4DF是解题的关键.
17.【分析】先可判断重叠部分为平行四边形,再由平行四边形的面积可得邻边相等,则重叠部分为菱形,然后由含30°角的直角三角形的性质求出BC=AB=4,最后根据平行四边形的面积公式求得即可.
【解答】解:过点A作AE⊥BC于E,AF⊥CD于F,如图所示:
∵两条纸条宽度相同,
∴AE=AF,
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,∠ABC=30°,
∵S ABCD=BC AE=CD AF,
又∵AE=AF,
∴BC=CD,
∴四边形ABCD是菱形,
∴AB=BC,
在Rt△AEB中,∠AEB=90°,∠ABC=30°,AE=2,
∴BC=AB=2AE=4,
∴四边形ABCD的面积=BC AE=4×2=8,
故答案为:8.
【点评】本题考查了菱形的判定与性质、平行四边形的判定与性质、含30°角的直角三角形的性质等知识,证得四边形ABCD为菱形是解题的关键.
18.【分析】由题意,G(﹣2,3),M(2,﹣3),根据等差点的定义可知,当直线y=x+b与矩形MNGH有两个交点时,矩形GHMN的边上存在两个点与点P是等差点,求出直线经过点G或M时的b的值即可判断.
【解答】解:由题意,G(﹣2,3),M(2,﹣3),
根据等差点的定义可知,当直线y=x+b与矩形MNGH有两个交点时,矩形GHMN的边上存在两个点与点P是等差点,
当直线y=x+b经过点G(﹣2,3)时,b=5,
当直线y=x+b经过点M(2,﹣3)时,b=﹣5,
∴满足条件的b的范围为:﹣5<b<5.
故答案为﹣5<b<5
【点评】本题考查一次函数图象上点的特征、矩形的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考填空题中的压轴题.
三、解答题(本大题共8小题,共66分解答应写出文字说明、证明过程或演算步骤)
19.【分析】直接把A点和B点坐标代入y=kx+b得到关于k、b的方程组,然后解方程组即可.
【解答】解:把A(1,3)、B(0,﹣2)代入y=kx+b得,解得,
所以此函数解析式为y=5x﹣2.
【点评】本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.
20.【分析】根据非负数的性质解得各边的长,再根据勾股定理的逆定理判定是否直角三角形.
【解答】解:△ABC为直角三角形,理由如下:
由题意得a﹣4=0,2b﹣12=0,10﹣c=0,
所以a=8,b=6,c=10,
因为82+62=102,
所以a2+b2=c2,
∴△ABC为直角三角形.
【点评】此题考查了勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.也考查了非负数的性质,解本题的关键是求出a,b,c的值.
21.【分析】(1)先证AM∥CN,再由平行四边形的性质得CM∥AN,然后由平行四边形的判定即可得出结论;
(2)根据平行四边形的性质解答即可.
【解答】(1)证明:∵AE⊥BD,CF⊥BD,
∴AM∥CN,
∵四边形ABCD是平行四边形,
∴CM∥AN,
∴四边形CMAN是平行四边形;
(2)解:∵四边形ABCD是平行四边形,
∴DC=AB,
∵四边形CMAN是平行四边形,
∴CM=AN,
∴CD﹣CM=AB﹣AN,
即DM=BN=2,
∴AB=AN+DM=3+2=5.
【点评】本题考查平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解题的关键.
22.【分析】(1)根据频数分布表中的数据,可以计算出本次调查的人数,然后即可计算出a和b的值;
(2)根据(1)中a的值,可以将频数分布直方图补充完整;
(3)根据频数分布表中的数据,可以计算出视力正常的人数占被调查人数的百分比.
【解答】解:(1)本次调查的人数为:20÷0.1=200,
a=200×0.25=50,b=10÷200=0.05,
故答案为:50,0.05;
(2)由(1)知,a=50,
补全的频数分布直方图如右图所示;
(3)(0.4+0.25+0.05)×100%=70%,
答:视力正常的人数占被调查人数的百分比是70%.
【点评】本题考查频数分布直方图、频数分布表,解答本题的关键是明确题意,利用数形结合的思想解答.
23.【分析】(1)根据甲,乙两种销售方案,分别得出两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,即单价×质量,列出即可;
(2)根据分析9x与8x+5000的大小关系,得出不等式的解集可以得出购买方案付款的多少问题.
【解答】解:(1)甲方案:每千克9元,由基地送货上门,
根据题意得:y=9x;x≥3000,
乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元,
根据题意得:y=8x+5000;x≥3000.
(2)根据题意可得:当9x=8x+5000时,
x=5000,
当购买5000千克时两种购买方案付款相同,
当大于5000千克时,9x>8x+5000,
∴甲方案付款多,乙付款少,
当小于5000千克时,9x<8x+5000,
∴甲方案付款少,乙付款多.
【点评】此题主要考查了一次函数的应用,得出两函数的解析式利用不等式即可得出付费的多少.
24.【分析】(1)由菱形的性质得出AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,得出∠BAD+∠ABC=180°,证出∠BAD=∠ABC,求出∠BAD=90°,即可得出结论;
(2)由正方形的性质得出AC⊥BD,AC=BD,CO=AC,DO=BD,得出∠COB=∠DOC=90°,CO=DO,证出∠ECO=∠EDH,证明△ECO≌△FDO(ASA),即可得出结论.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,
∴∠BAD+∠ABC=180°,
∵∠CAD=∠DBC,
∴∠BAD=∠ABC,
∴2∠BAD=180°,
∴∠BAD=90°,
∴四边形ABCD是正方形;
(2)解:∵四边形ABCD是正方形,AB=BC=4,
∴AC⊥BD,AC=BD=4,
∴OB=CO=AC=2,DO=BD=2,
∴∠COB=∠DOC=90°,CO=DO,
∵DH⊥CE,垂足为H,
∴∠DHE=90°,∠EDH+∠DEH=90°,
∵∠ECO+∠DEH=90°,
∴∠ECO=∠EDH,
在△ECO和△FDO中,
,
∴△ECO≌△FDO(ASA),
∴OE=OF.
∵BE=1,
∴OE=OF=OB﹣BE=2﹣1.
【点评】本题考查了正方形的判定与性质、菱形的性质,全等三角形的判定与性质等知识;熟练掌握正方形的判定与性质是解题关键.
25.【分析】(1)由折叠得到∠DOB=∠AOB,再由BC∥OA得到∠OBC=∠AOB,即∠OBC=∠DOB,即可得出结论;
(2)由(1)得到EO=EB设OE=x则CE=8﹣x,再用勾股定理建立方程16+(8﹣x)2=x2,求出x即可;
(3)设出点P坐标,分三种情况,根据等腰三角形的性质即可求解.
【解答】(1)证明:∵将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
∴∠DOB=∠AOB,
∵四边形OABC是长方形,
∴BC∥OA,
∴∠OBC=∠AOB,
∴∠OBC=∠DOB,
∴EO=EB;
(2)解:由(1)得,EO=EB,
∵长方形OABC的顶点A,C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),
设OE=BE=x,则CE=8﹣x,
在Rt△OCE中,OC=4,根据勾股定理得,OC2+CE2=OE2,
∴16+(8﹣x)2=x2,
∴x=5,
∴BE=5,
∴CE=3,
∴E(3,4);
(3)解:点B的坐标为(8,4),
∴直线OB解析式为y=x,
∵点P是直线OB上的任意一点,
∴设P(a, a),
∵O(0,0),C(0,4),
∴OC=4,PO2=a2+(a)2=a2,PC2=a2+(4﹣a)2,
∵△OPC是等腰三角形,
①当PO=PC时,PO2=PC2,
∴a2=a2+(4﹣a)2,
∴a=4,
∴P(4,2);
②当PO=OC时,PO2=OC2,
∴a2=16,
∴a=±,
∴P(,)或P(﹣,﹣);
③当PC=OC时,PC2=OC2,
∴a2+(4﹣a)2=16,
∴a=0(舍)或a=,
∴P(,);
∴满足条件的点P的坐标为(4,2)或(,)或P(﹣,﹣)或(,).
【点评】此题是四边形综合题,主要考查了矩形的性质,折叠的性质,勾股定理,等腰三角形的性质,解本题的关键求出点E的坐标,学会用分类讨论的思想思考问题.
26.【分析】(1)平行四边形的性质可得AD∥BC,AB∥CD,再根据平行线的性质证明∠CEF=∠CFE,根据等角对等边可得CE=CF,再有条件四边形ECFG是平行四边形,可得四边形ECFG为菱形,即可解决问题;
(2)先判断出∠BEG=120°=∠DCG,再判断出AB=BE,进而得出BE=CD,即可判断出△BEG≌△DCG(SAS),再判断出∠CGE=60°,进而得出△BDG是等边三角形,即可得出结论;
(3)首先证明四边形ECFG为正方形,再证明△BME≌△DMC可得DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到△BDM是等腰直角三角形,由等腰直角三角形的性质即可得到结论.
【解答】解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图2中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DM=BD=5.
【点评】此题主要考查平行四边形的判定方法,全等三角形的判定与性质,等边三角形的判定与性质,菱形的判定与性质等知识点,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.
同课章节目录
