人教版六年级上册《圆》的练习课 课件(共19张PPT)
文档属性
| 名称 | 人教版六年级上册《圆》的练习课 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-07 07:22:43 | ||
图片预览


文档简介
(共19张PPT)
展示学生去前测作品
学生梳理圆思维导图的照片
说一说:你找到了哪些信息,用什么方法找到的。
圆 练习课
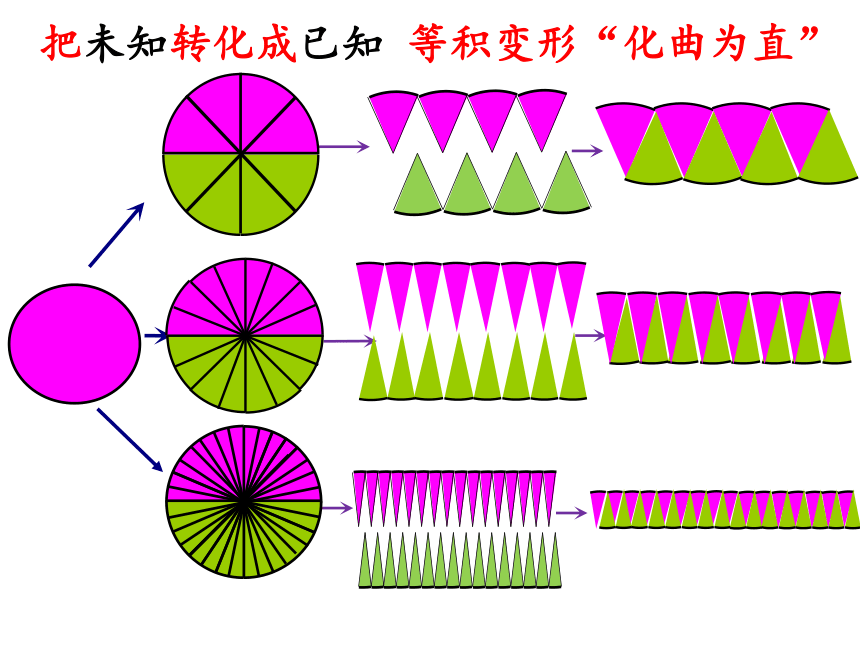
把未知转化成已知 等积变形“化曲为直”
底
高
圆的面积
圆周长的一半
平行四边形的面积= 底 × 高
平行四边形的面积
圆的半径
×
×
圆的面积
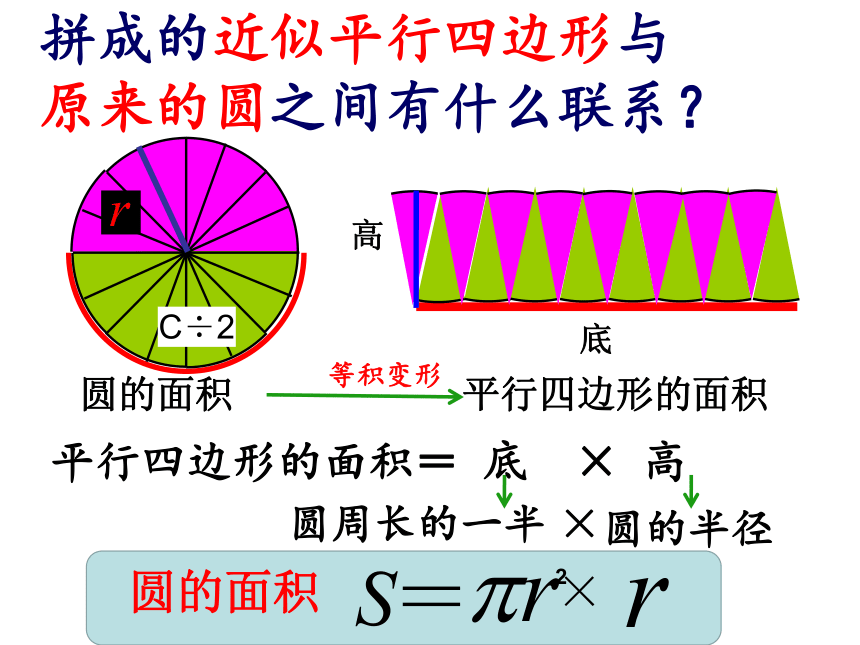
拼成的近似平行四边形与
原来的圆之间有什么联系?
C÷2
2
等积变形
1.羊主人买来一只羊,用1根长5米的绳子拴
在草地上。羊最多能吃到多少面积的草?
o
5m
.
2.羊主人觉得绳子太长,把绳子剪短2米,
现在羊吃到草面积最大是多少?羊吃到草的
面积减少了多少?(可以画一画帮助解决)
o
3m
.
5m
3.14×5 - 3.14×3 = 28.26(㎡)
阴影部分的面积。
R=5cm
r=3cm
3.14×5 - 3.14×3 = 28.26(㎡)
S圆环=S大圆-S小圆
r=3cm
R=5cm
r=3cm
R=5cm
S阴影=S大圆-S小圆
3.14×5 - 3.14×3 = 28.26(㎡)
r=3cm
R=5cm
①
②
1号阴影部分比2号阴影部分大多少?
S① — S②
=(S①+S空白)—(S②+S空白)
3.14×5 - 3.14×3 = 28.26(㎡)
=S大圆 — 小圆
3.傍晚,羊主人把羊牵回到半径4米的靠墙羊圈,这羊圈的面积是多少?修这个羊圈需要多长的栅栏?请在图上画出羊圈。(声响开始声停结束)
3.14×4×4÷2=25.12(平方米)
4.第二天羊主人又把羊拴在边长为3米的正方形
建筑物的一个顶点上,绳长为6米,此时羊的活动区域有多大?请画出羊的活动区域。
活动要求:
1.到学习组长处一起用正方体当房子,相互
合作一起用绳子转一转,组内成员试过都之后
回到自己位置开始画一画,算一算。
边长3米 绳长6米
房子
组合图形的面积
S阴=S圆- 2S三角形
o
r=3cm
S阴=3.14×3×3 - 3×6÷2
=3.14×3×3 - 3×3
=19.26(cm)
圆中方问题
组合图形的面积
o
.
方中圆问题
r=3cm
S阴=6×6 -3.14×9 =36-28.26
=7.74(cm )
S阴=S正-S圆
5.下图正方形的面积是12平方厘米,求图中阴影部分的面积。
课堂感想
1、这节课你有什么收获?
2、这节课还有什么疑惑?
说出来和大家一起交流吧!
如图所示,一块边长为8m的正方形草地,在图中相对的顶点处各拴有一只羊,拴羊的绳长都是8m.两只羊都能吃到草的草地面积(阴影部分)是多少平方米?
3.14×8 ÷2-8 =36.48(平方米)
答:两只羊都能吃到草的草地面积(阴影部分)是36.48平方米。
展示学生去前测作品
学生梳理圆思维导图的照片
说一说:你找到了哪些信息,用什么方法找到的。
圆 练习课
把未知转化成已知 等积变形“化曲为直”
底
高
圆的面积
圆周长的一半
平行四边形的面积= 底 × 高
平行四边形的面积
圆的半径
×
×
圆的面积
拼成的近似平行四边形与
原来的圆之间有什么联系?
C÷2
2
等积变形
1.羊主人买来一只羊,用1根长5米的绳子拴
在草地上。羊最多能吃到多少面积的草?
o
5m
.
2.羊主人觉得绳子太长,把绳子剪短2米,
现在羊吃到草面积最大是多少?羊吃到草的
面积减少了多少?(可以画一画帮助解决)
o
3m
.
5m
3.14×5 - 3.14×3 = 28.26(㎡)
阴影部分的面积。
R=5cm
r=3cm
3.14×5 - 3.14×3 = 28.26(㎡)
S圆环=S大圆-S小圆
r=3cm
R=5cm
r=3cm
R=5cm
S阴影=S大圆-S小圆
3.14×5 - 3.14×3 = 28.26(㎡)
r=3cm
R=5cm
①
②
1号阴影部分比2号阴影部分大多少?
S① — S②
=(S①+S空白)—(S②+S空白)
3.14×5 - 3.14×3 = 28.26(㎡)
=S大圆 — 小圆
3.傍晚,羊主人把羊牵回到半径4米的靠墙羊圈,这羊圈的面积是多少?修这个羊圈需要多长的栅栏?请在图上画出羊圈。(声响开始声停结束)
3.14×4×4÷2=25.12(平方米)
4.第二天羊主人又把羊拴在边长为3米的正方形
建筑物的一个顶点上,绳长为6米,此时羊的活动区域有多大?请画出羊的活动区域。
活动要求:
1.到学习组长处一起用正方体当房子,相互
合作一起用绳子转一转,组内成员试过都之后
回到自己位置开始画一画,算一算。
边长3米 绳长6米
房子
组合图形的面积
S阴=S圆- 2S三角形
o
r=3cm
S阴=3.14×3×3 - 3×6÷2
=3.14×3×3 - 3×3
=19.26(cm)
圆中方问题
组合图形的面积
o
.
方中圆问题
r=3cm
S阴=6×6 -3.14×9 =36-28.26
=7.74(cm )
S阴=S正-S圆
5.下图正方形的面积是12平方厘米,求图中阴影部分的面积。
课堂感想
1、这节课你有什么收获?
2、这节课还有什么疑惑?
说出来和大家一起交流吧!
如图所示,一块边长为8m的正方形草地,在图中相对的顶点处各拴有一只羊,拴羊的绳长都是8m.两只羊都能吃到草的草地面积(阴影部分)是多少平方米?
3.14×8 ÷2-8 =36.48(平方米)
答:两只羊都能吃到草的草地面积(阴影部分)是36.48平方米。
