苏科版七年级上册2.4.1绝对值课件(共13张PPT)
文档属性
| 名称 | 苏科版七年级上册2.4.1绝对值课件(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
2.4 绝对值与相反数
苏科版初中数学七年级上第2章有理数
第一课时 绝对值
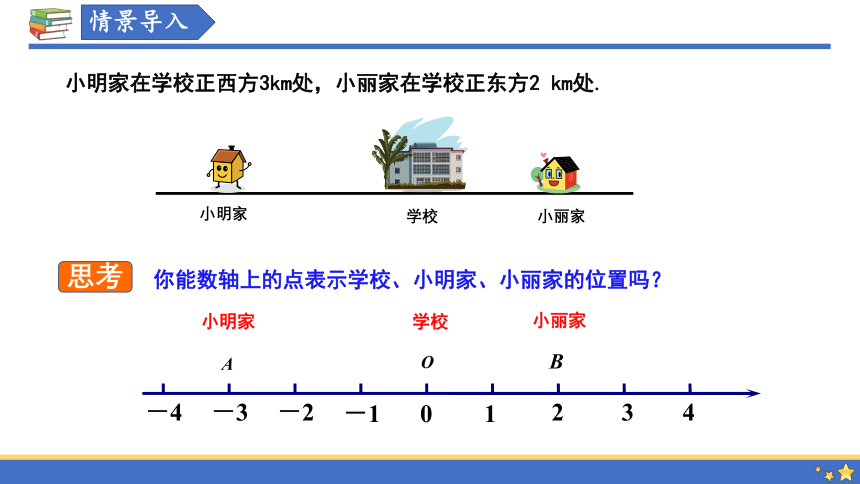
小明家在学校正西方3km处,小丽家在学校正东方2 km处.
小明家
学校
小丽家
你能数轴上的点表示学校、小明家、小丽家的位置吗?
思考
A
B
4
3
2
1
0
-1
-2
-3
-4
小明家
小丽家
学校
O
假如他们步行的速度相同,谁先到学校?为什么?
表示-3的点A与原点的距离是 ;
表示2的点B与原点的距离是 .
3个单位长度
2个单位长度
数轴上表示一个数的点与原点的距离,叫做这个数的绝对值.
表示0的点就是原点,与原点的距离是0,所以0的绝对值是0.
A
B
4
3
2
1
0
-1
-2
-3
-4
小明家
小丽家
学校
O
思考
概念
非负的
-3的绝对值是3
2的绝对值是2
非负性
点表示的数的绝对值为;
你能说出数轴上的点所表示的数的绝对值吗?
点表示的数的绝对值为;
点表示的数的绝对值为;
点表示的数的绝对值为;
点表示的数的绝对值为.
到原点距离是5的数有 个,
所以绝对值是5的数是 .
观察思考
3.5
4
因为点与原点的距离是,所以的绝对值是;
因为点与原点的距离是,所以的绝对值是.
解:在数轴上分别画出表示的点、点.
B
A
例1
求的绝对值.
归纳
有理数的绝对值的求法:
1.画数轴,标出有理数所在点,
得到点到原点的距离;
2.求得有理数的绝对值.
有理数
绝对值
点
距离
一个数的绝对值有没有更简洁的表示方法呢?
思考
通常,我们将数的绝对值记为 .
4的绝对值表示为:
-3.5的绝对值表示为:
∣0∣
0的绝对值表示为:
因为点、点表示的数分别是 、 ,
所以绝对值是 的数有2个,它们是 、.
B
A
例2
已知一个数的绝对值是 ,求这个数.
解:数轴上到原点的距离是 的点有2个,它们分别是点和点.
1.填空:
5
0.4
0
5
2
2.的符号是____,绝对值是____, 的符号是_____,绝对值是____.
3.在数轴上离原点距离是3的数是__ __,
绝对值小于3的整数是__ ___,
绝对值不大于3的整数__ ___,
绝对值不大于3的非负整数是__ ___.
4.绝对值最小的有理数是 ( )
A.1 B.0 C.-1 D.不存在
5.绝对值最小的整数是( )
A.-1 B.1 C.0 D.不存在
6.绝对值小于3的负数的个数有( )
A.2 B.3 C.4 D.无数
7.,则等于( )
A.2 B.-2 C.2或-2 D.不存在
9.判断题
(1)任何一个有理数的绝对值都是正数. ( )
(2)如果一个数的绝对值是12,则这个数是12. ( )
(3)绝对值小于5的整数有4,3,2,1,0. ( )
8.下列说法中,错误的是( )
A.+5的绝对值等于5 B.绝对值等于5的数是5
C.-5的绝对值是5 D.+5、-5的绝对值相等
10.比较-3与-6的绝对值的大小.
, ,
且,
解:在数轴上分别画出表示-3、-6的点A、点B
6
0
1
2
4
3
-3
6
5
-1
-2
-4
-5
-6
3
A
B
,
即的绝对值小于的绝对值.
因为我们把数轴上表示一个数的点到原点的距离看成这个数的绝对值,因此,任意一个有理数的绝对值都是非负数.
绝对值
概念
表示
方法
非负性
数轴上表示一个数的点与原点的距离叫做这个数的绝对值.表示0的点就是原点,与原点的距离是0,所以0的绝对值是0.
绝对值用“| |”表示,如数的绝对值记为
谢 谢!
2.4 绝对值与相反数
苏科版初中数学七年级上第2章有理数
第一课时 绝对值
小明家在学校正西方3km处,小丽家在学校正东方2 km处.
小明家
学校
小丽家
你能数轴上的点表示学校、小明家、小丽家的位置吗?
思考
A
B
4
3
2
1
0
-1
-2
-3
-4
小明家
小丽家
学校
O
假如他们步行的速度相同,谁先到学校?为什么?
表示-3的点A与原点的距离是 ;
表示2的点B与原点的距离是 .
3个单位长度
2个单位长度
数轴上表示一个数的点与原点的距离,叫做这个数的绝对值.
表示0的点就是原点,与原点的距离是0,所以0的绝对值是0.
A
B
4
3
2
1
0
-1
-2
-3
-4
小明家
小丽家
学校
O
思考
概念
非负的
-3的绝对值是3
2的绝对值是2
非负性
点表示的数的绝对值为;
你能说出数轴上的点所表示的数的绝对值吗?
点表示的数的绝对值为;
点表示的数的绝对值为;
点表示的数的绝对值为;
点表示的数的绝对值为.
到原点距离是5的数有 个,
所以绝对值是5的数是 .
观察思考
3.5
4
因为点与原点的距离是,所以的绝对值是;
因为点与原点的距离是,所以的绝对值是.
解:在数轴上分别画出表示的点、点.
B
A
例1
求的绝对值.
归纳
有理数的绝对值的求法:
1.画数轴,标出有理数所在点,
得到点到原点的距离;
2.求得有理数的绝对值.
有理数
绝对值
点
距离
一个数的绝对值有没有更简洁的表示方法呢?
思考
通常,我们将数的绝对值记为 .
4的绝对值表示为:
-3.5的绝对值表示为:
∣0∣
0的绝对值表示为:
因为点、点表示的数分别是 、 ,
所以绝对值是 的数有2个,它们是 、.
B
A
例2
已知一个数的绝对值是 ,求这个数.
解:数轴上到原点的距离是 的点有2个,它们分别是点和点.
1.填空:
5
0.4
0
5
2
2.的符号是____,绝对值是____, 的符号是_____,绝对值是____.
3.在数轴上离原点距离是3的数是__ __,
绝对值小于3的整数是__ ___,
绝对值不大于3的整数__ ___,
绝对值不大于3的非负整数是__ ___.
4.绝对值最小的有理数是 ( )
A.1 B.0 C.-1 D.不存在
5.绝对值最小的整数是( )
A.-1 B.1 C.0 D.不存在
6.绝对值小于3的负数的个数有( )
A.2 B.3 C.4 D.无数
7.,则等于( )
A.2 B.-2 C.2或-2 D.不存在
9.判断题
(1)任何一个有理数的绝对值都是正数. ( )
(2)如果一个数的绝对值是12,则这个数是12. ( )
(3)绝对值小于5的整数有4,3,2,1,0. ( )
8.下列说法中,错误的是( )
A.+5的绝对值等于5 B.绝对值等于5的数是5
C.-5的绝对值是5 D.+5、-5的绝对值相等
10.比较-3与-6的绝对值的大小.
, ,
且,
解:在数轴上分别画出表示-3、-6的点A、点B
6
0
1
2
4
3
-3
6
5
-1
-2
-4
-5
-6
3
A
B
,
即的绝对值小于的绝对值.
因为我们把数轴上表示一个数的点到原点的距离看成这个数的绝对值,因此,任意一个有理数的绝对值都是非负数.
绝对值
概念
表示
方法
非负性
数轴上表示一个数的点与原点的距离叫做这个数的绝对值.表示0的点就是原点,与原点的距离是0,所以0的绝对值是0.
绝对值用“| |”表示,如数的绝对值记为
谢 谢!
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
