人教版七年级上册2整式的加减复习(共63张PPT)
文档属性
| 名称 | 人教版七年级上册2整式的加减复习(共63张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1007.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-07 16:28:55 | ||
图片预览









文档简介
(共63张PPT)
第二章 整式加减
章小结
整式
单项式
多项式
知识结构
整式的加减
同类项
升降幂排列
易错题总结
重点题
补充例题
补充两题
单多项式练习
去括号小练习
你说我说
大家说
整式的加减
常见题型
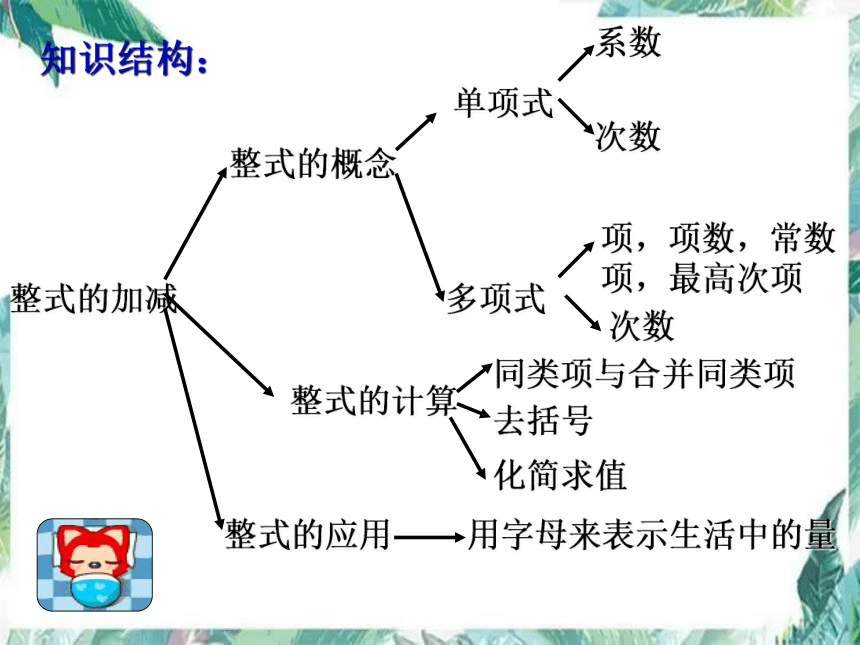
知识结构:
整式的加减
整式的概念
整式的计算
整式的应用
单项式
多项式
系数
次数
项,项数,常数项,最高次项
次数
同类项与合并同类项
去括号
化简求值
用字母来表示生活中的量
单项式
表示数与字母或字母与字母的积的式子叫做单项式(Monomial) 。
单独的数字或字母也叫单项式。
例如:3,-6,a,axy,6x
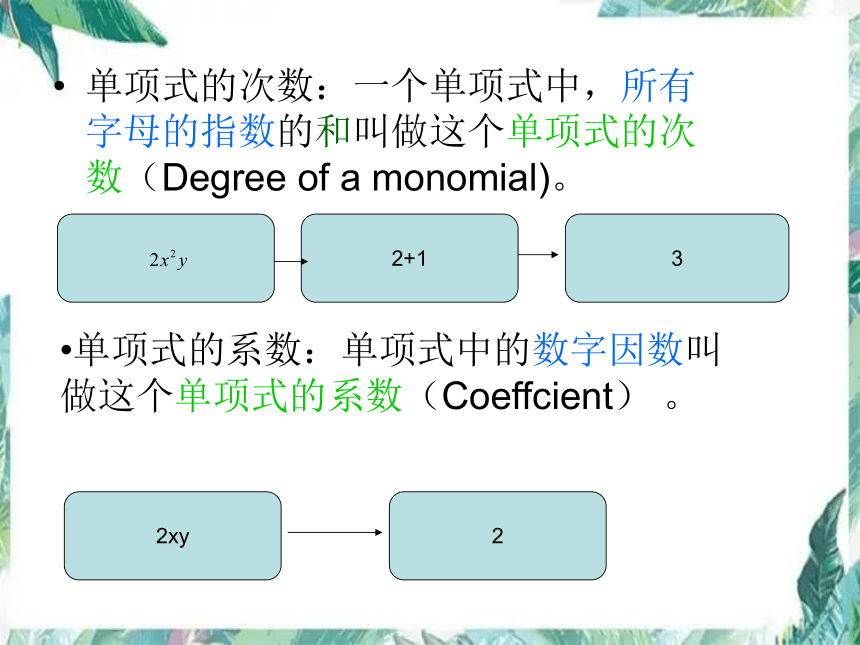
单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数(Degree of a monomial)。
3
2+1
2xy
2
单项式的系数:单项式中的数字因数叫做这个单项式的系数(Coeffcient) 。
定义:
单项式中的_________。
次数:
1.当单项式的系数是1或-1时,“1”通常省略不写。
单项式:
系数:
数字与字母或字母与字母的乘积
由________________ 组成的式子。
单独的______或________ 也是单项式。
单项式中的__________________.
数字因数
所有字母的指数和
一个数
一个字母
注意的问题:
2.当式子分母中出现字母时不是单项式。
3.圆周率π是常数,不要看成字母。
4.当单项式的系数是带分数时,通常写成假分数。
5.单项式的系数应包括它前面的性质符号。
6.单项式次数是指所有字母的次数的和,与数字的次数没有关系。
7.单独的数字不含字母, 规定它的次数是零次.
1xy=xy、-1x=-x
2/a
×
3xy-xy
单项式注意:
1,分母含有字母的式子不属于单项式。因为单项式属于整式,而分母含有未知数的式子是分式。例如,1/x不是单项式。
2,单独的一个数字或字母也是单项式。例如,1和x^2y也是单项式。
3,单项式表示数与字母相乘时,通常把数写在前面。
如果一个单项式,只含有字母因数,如果是正数的单项式系数为1,如果是负数的单项式系数为-1。
如果一个单项式,只含有数字因数,那么它的次数为0。
单项式概念:
1.任意一个字母和数字的积的形式的代数式(除法中有:除以一个数等于乘这个数的倒数)。
2.单独一个字母或数字也叫单项式。
3.分母中不含字母(单项式是整式,而不是分式)
a,-5,1X,2XY,都是单项式,而0.5m+n,不是单项式。
4,0也是数字,也属于单项式。
5,有分数也属于单项式。
单项式的次数是指单项式中所有字母因数的指数和
这个名词是清代数学家李善兰译书时根据原词概念汉化的。
单项式是字母与数的乘积。
单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数。
单项式的系数:单项式中的数字因数。如:2xy的系数是2;-5zy 的系数是-5
字母t的指数是1,100t是一次单项式;在单项式vt中,字母v与t的指数的和是2,vt是二次单项式。
如:xy ,3,a z,ab,b ...... 都是单项式。
用运算符号把表示数的字母或数连接起来的式子叫代数式。
代数式不含有“≥”、“=”、“<”、“≠”符号等
单项式书写规则:数与字母相乘时,数在字母前;乘号可以省略为点或不写;除法的式子可以写成分数式;带分数与字母相乘,带分数要化为假分数
单项式是几次,就叫做几次单项式
字母不能在分母中(因为这样为分式,不为单项式)
“π”是特指的数,不是字母,读pài。
单项式书写格式:
1.数字写在字母的前面,应省略乘号。[5a 、16xy等]
2.π是常数,因此也可以作为系数。
3.若系数是带分数,要化成假分数。
4.当一个单项式的系数是1或-1时,“1”通常省略不写,如[(-1)ab ]写成[ -ab ]等。
5.在单项式中字母不可以做分母,分子可以。
6.单项式中系数不为0,否则单项无意义。
7.单独的数“0”的系数是零,次数也是零。
8.常数的系数是它本身,次数为零
单项式的计算:
单项式加减法则
单项式加减即合并同类项,也就是合并前各同类项系数的和,字母不变。
例如:3a+4a=7a,9a-2a=7a等单项式乘法法则
单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式
例如:3a·4a=12a^2单项式除法法则
同底数幂相除,底数不变,指数相减。
例如:9a^10÷3a^5=3a^5
多项式
若干个单项式的和组成的式子叫做多项式 。
例如:1/2a+3xy-4y
多项式的项:多项式中每个单项式叫做多项式的项 。
多项式的次数:这些单项式中的最高次数,就是这个多项式的次数。
多项式的常数项:多项式中的数字项,叫做多项式的常数项。
2
定义:几个__________.
常数项:多项式中_______________.
多项式的次数:_________________________.
项: 组成多项式中的_____________.
有几项,就叫做_________.
1.在确定多项式的项时,要连同它前面的符号,
2.一个多项式的次数最高项的次数是几,就说这个多项式是几次多项式。
3.在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念。
多项式
单项式的和
每一个单项式
几项式
不含字母的项
多项式中次数最高的项的次数。
注意的问题:
一、知识梳理:(不看课本,把下列空填写在横线上。若遇到不会的可翻阅课本)
1、由 或 的 组成的式子叫单项式。
单独的一个 或 也是单项式.
2、单项式中的 叫单项式的系数。所有 的指数的 叫单项式的次数。
3、几个单项式的 叫多项式。
4、式中的每个 叫多项式的项。(其中不含字母的项叫做 )
5、多项式中次数最 的项的次数叫多项式的次数。
6、多项式的每一项都包括它前面的 .
第一块复习
整式的加减
整式的加减
同类项
升降幂排列
整式的加减混合运算步骤(有括号先去括号)
1.找同类项,做好标记。
2.利用加法的交换律和结合律把同类项放在一起。
3.利用乘法分配律计算结果。
4.按要求按“升”或“降”幂排列。
找
搬
并
排
1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同。
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
“去括号,看符号。是‘+’号,不变号,是‘-’号,全变号”
一:去括号
二:计算
(按照先小括号,再中括号,最后大括号的顺序)
同类项的定义:
(两相同)
合并同类项概念:
_________________________.
合并同类项法则:
2._________________不变。
2._________________相同。
1.____相同,
字母
相同的字母的指数也
1.______相加减;
字母和字母的指数
系数
同类项
注意:几个常数项也是______
同类项。
(两无关)
2.与__________无关。
1.与____无关
系数
字母的位置
把多项式中的同类项合并成一项
掌握同类项的概念时注意:
1.判断几个单项式或项,是否是同类项,就要掌握两个条件:
①所含字母相同。
②相同字母的次数也相同.
2.同类项与系数无关,与字母排列的顺序也无关。
3.所有常数项都是同类项。
解:4x2 - 8x + 5-3x2 + 6x -4
~~~ ~~~
=(4x2-3x2)
= x2
合并同类项的步骤:
1、找出同类项
用不同的线标记出各组同类项,注意每一项的符号。
2、把同类项移在一起
用括号将同类项结合,括号间用加号连接。
3、合并同类项
系数相加,字母及字母的指数不变 。
(-8x+6x)
(5-4)
-2x
+1
2.合并多项式4x2-8x+5-3x2+6x-4中的同类项.
— ——
要记住呀!!
+ +
一找
二移
三并
2.若 与 是同类项,则m+n=___.
4.若 ,则m+n-p=______
5
4
3.若 与 的和是一个单项式,则 =___.
-4
1.下列各式中,是同类项的是:___________
① 与
② 与
③ 与
④ 与
⑤ 与
⑥-125与
③⑤⑥
同类项练习
1.下列各组中的两项是不是同类项?为什么?
(1) (2)
(3) (4)
(5) (6)
比一比,谁最棒
2.试一试,我能行
1、下列各组是同类项的是( )
A 2x3与3x2 B 12ax与8bx
C x4与a4 D π与-3
2、5x2y 和42xnym是同类项,则
m=______, n=________
3、 –xmy与45ynx3是同类项,则
m=_______. n=______
D
1
2
3
1
1.填空,并解释其中依据:
(1)
(2)
(3)
合并同类项:
定义:把多项式中的同类项合并成一项
法则:(1)系数:系数相加;
(2)字母:字母和字母的指数保持不变。
方法:逆用乘法分配律可以把同类项进行合并,合并时,把它们的系数相加作为新的系数,而字母部分不变。
3.合并下列多项式中的同类项:
(3)2a2-3ab+4b2+5ab-6b2
升、降幂排列
1.把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把多项式按这个字母降幂排列。
2.把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把多项式按这个字母升幂排列。
练习
下面的数中,哪些是单项式,哪些是多项式,哪些是整式?
-9,xyz,-x+3-xy,3.14+xy-5+2x
单项式: -9,xyz
多项式: -x+3-xy,3.14+xy-5+2x
整式: -9,xyz,-x+3-xy,3.14+xy-5+2x
去括号:
1-xy
-9xy-5xyz-9+7y
-(-1+xy)=
-9xy-(5xyz+9-7y)=
整式的加减的常见题型
1.实际问题
2.直接化简代入
3.条件求值
4.整体代入
求代数式的值
一、概念中的易错题
二、运算中的易错题
易错点总结:
注意:有多重括号的,一般先去小括号,再去中括号,最后再去大括号;
(先去括号)
(降幂排列)
(合并同类项,化简完成)
当x=-2时
(代入)
(代入时注意添上括号,乘号改回“×”)
单项式的定义
例1,下列各式子中,是单项式的有______________(填序号)
①、②、④、⑦
注意:1,单个的字母或数字也是单项式;
2,用加减号把数字或字母连接在一起
的式子不是单项式;
3,只用乘号把数字或字母连接在一起
的式子仍是单项式;
4,当式子中出现分母时,要留意分母里有
没有字母,有字母的就不是单项式,如
果分母没有字母的仍有可能是单项式
(注:“π”当作数字,而不是字母)
单项式的系数与次数
单项式
系数
次数
例2 指出下列单项式的系数和次数;
注意:1,字母的系数“1” 可以省略的,但不代表没有系
数(次数也是同样道理);
2,有分母的单项式,分母中的数字也是单项式系
数的一部分;
3,注意“π”不是字母,而是数字,属于系数的一
部分;
4,计算次数的时候并不是简单的见到指数就相
加,注意单项式的次数指的是字母的指数和;
多项式的项数与次数
例3 下列多项式次数为3的是( )
C
例4 请说出下列各多项式是几次几项式,并写出多项式的最高次项和常数项;
注意(1)多项式的次数不是所有项的次数的和,而是它的最高
次项次数;
(2)多项式的每一项都包含它前面的符号;
(3)再强调一次, “π”当作数字,而不是字母
书写格式中的易错点
例5 下列各个式子中,书写格式正确的是( )
1、代数式中用到乘法时,若是数字与数字乘,要用“×”
若是数字与字母乘,乘号通常写成”.”或省略不写,如
3×y应写成3·y或3y,且数字与字母相乘时,字母与
字母相乘,乘号通常写成“·”或省略不写。
2、带分数与字母相乘,要写成假分数
3、代数式中出现除法运算时,一般用分数写,即用分数
线代替除号。
4、系数一般写在字母的前面,且系数“1”往往会省略;
F
例6 王强班上有男生m人,女生比男生的一半多5人,王强班上的总人数(用m表示)为______人。
易错点:结果不进行化简,直接写
点拨:结果中有 它们是同类项,应合并以保证最后的结果最简.正确的写法是
同类项的判定与合并同类项的法则:
例1 判断下列各式是否是同类项?
点拨:对于(1)、(3),考察的是同类项的定义,所含字母相同,相同字母的指数也相同的称为同类项;所以(1)、(3)不是同类项;
对于(2),虽然好像它们的次数不一样,但其实它们都是常数项,所以,它们都是同类项;
对于(4),虽然它们的系数不同,字母的顺序也不同,但它依然满足同类项的定义,是同类项;
答:(2)、(4)是同类项,(1)(3)不是同类项;
例2 下列合并同类项的结果错误的有_______________.
①、②、③、④、⑤
注意:1,合并同类项的法则是把同类项的系数相加,字母和字母的次数不变;
2,合并同类项后也要注意书写格式;
3,如果两个同类项的系数互为相反数,那么合并同类项后,结果得____;
0
去括号中的易错题:
1,判断下列各式是否正确:
√
×
×
( )
( )
( )
×
( )
去括号时,1,注意括号外面的符号,括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不用变符号;括号前面是“—”号,把括号和它前面的“—”号去掉,括号里各项都改变符号。
2,注意外面有系数的,各项都要乘以那个系数;
例3 合并同类项:
小明的解法:
(1)错在把所有项都当作同类项了;
正确的解法:
例3 合并同类项:
小明的解法:
(2)错在把结合同类项时弄错了符号;
正确的解法:
总之,合并同类项现要找出式子中的同类项,并把它们写在一起,最后合并,注意同类项的系数是带符号的。
去括号中的易错题:
1、判断下列各式是否正确:
√
×
×
( )
( )
( )
×
( )
去括号时,1,注意括号外面的符号,括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不用变符号;括号前面是“—”号,把括号和它前面的“—”号去掉,括号里各项都改变符号。
2,注意外面有系数的,各项都要乘以那个系数;
练一练:
1,化简下列各式:
整式的加减一般步骤是(1)如果有括号就先去括号,(2)然后再合并同类项.
多重括号化简的易错题
注意:有多重括号的,一般先去小括号,再去中括号,最后再去大括号;
化简求值中的易错题:
(先去括号)
(降幂排列)
(合并同类项,化简完成)
当x=-2时
(代入)
(代入时注意添上括号,乘号改回“×”)
1.去掉下列各式中的括号。
(1)8m-(3n+5)
(2)n-4(3-2m)
(3)2(a-2b)-3(2m-n)
=8m-3n-5
=n-12+8m
=2a-4b-6m+3n
2.化简:
-(3x-2y+z)-[5x-x+2y-z-3x]
解:原式=
-(3x-2y+z)-[5x-(x-2y+z)-3x]
=-(3x-2y+z)-[x+2y-z]
=-(3x-2y+z)-[(5x-x-3x)+2y-z]
=-3x+2y-z-x-2y+z
=(-3x-x)+(2y-2y)+(-z+z)
=-4x
“A+2B”类型的易错题:
例1 若多项式 计算多项式A-2B;
注意:列式时要先加上括号,再去括号;
例2 一个多项式A加上 得 ,求这个多项式A?
注意:我们在移项的时候是整体移项,不要漏了添上括号;
2,实际问题中的易错题:
例1 某种手机卡的市话费上次已按原收费标准降低了m元/分钟,现在再次下调20%,使收费标准为n元/分钟,那么原收费标准为 ( ).
B
点拨:为了弄清各数之间的关系,我们可以借助方程来求解.假设原收费标准为每分钟x元,可得:
解得 .应选B.
例2 若长方形的一边长为a+2b,另一边长比它的3倍少a-b,求这个长方形的周长?
分析:如果直接列式的话,非常麻烦,我们可以先求出另一边长,再求周长,这样就比较容易求出答案;
解:一边长为:a+2b;
另一边长为:3(a+2b)-(a-b)
=3a+6b-a+b
=3a-a+6b+b
=2a+7b;
周长为:2(a+2b+2a+7b)
=2(a+2a+2b+7b)
=2(3a+9b)
=6a+18b;
答:长方形的周长为6a+18b
从错误中吸取教训,
从失败中取得进步,
完善完整知识网络,
我将会成为最棒的!
第n个图案中有地砖 块.
重点题,考试必考
求当x= 时,多项式
的值。
解:原式=
=
=
把x= 带入 中,得
∴ 原式=5
补充例题:
a
0
b
已知数a,b在数轴上的位置如图所示
化简下列式子:
∴原式=-a-2[-(a+b)]-3(b-a)
解:由题意知:a<0,b>0且|a|>|b|
=-a+2[a+b]-3b+3a
=-a+2a+2b-3b+3a
=(-a+2a+3a)+(2b-3b)
=4a-b
当x=1时, 则当x=-1时,
解:将x=1代入 中得:
a+b-2=3
∴ a+b=5;
当x=-1时
=-a-b-2
=-(a+b)-2
=-7
=-5-2
若-5a3bm+1与8an+1b2是同类项,求(m-n)100的值。
解:由同类项的定义知:m+1=2,n+1=3;解得m=1,n=2
∴(m-n)100=(1-2)100=(-1)100=1
答:当m=1,n=2时,(m-n)100=1。
评析:例1要注意同类项概念的应用;例2要注意几位数的表示方法。如:578=5×100+7×10+8。
如果一个两位数的个位数是十位数的4倍,那么这个两位数一定是7的倍数。请说明理由。
解:设两位数的十位数字是x,则它的个位数字是4x。
∴这个两位数可表示为:10x+4x=14x,
∵14x是7的倍数,故这个两位数是7的倍数。
已知多项式A= ,B= ,C=
求 2A-5B+3C=
解:原式=
=
=
=
如果关于x的多项式 的值与x
无关,则a的取值为_____.
解:原式=
由题意知,则:
6a-6=0
∴a=1
1
如果关于x,y的多项式 的差
不含有二次项,求 的值。
解:原式=
由题意知,则:
m-3=0
2+2n=0
∴m=3,n=-1;
∴ = =-1
1.指出下各式的关系(相等、相反数、不确定):
(1) a-b与b-a
(2) -a-b与-(b-a)
(3) –(a-b)与b-a
(4) –(a-b)与b-a
2.
补充两题:
第二章 整式加减
章小结
整式
单项式
多项式
知识结构
整式的加减
同类项
升降幂排列
易错题总结
重点题
补充例题
补充两题
单多项式练习
去括号小练习
你说我说
大家说
整式的加减
常见题型
知识结构:
整式的加减
整式的概念
整式的计算
整式的应用
单项式
多项式
系数
次数
项,项数,常数项,最高次项
次数
同类项与合并同类项
去括号
化简求值
用字母来表示生活中的量
单项式
表示数与字母或字母与字母的积的式子叫做单项式(Monomial) 。
单独的数字或字母也叫单项式。
例如:3,-6,a,axy,6x
单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数(Degree of a monomial)。
3
2+1
2xy
2
单项式的系数:单项式中的数字因数叫做这个单项式的系数(Coeffcient) 。
定义:
单项式中的_________。
次数:
1.当单项式的系数是1或-1时,“1”通常省略不写。
单项式:
系数:
数字与字母或字母与字母的乘积
由________________ 组成的式子。
单独的______或________ 也是单项式。
单项式中的__________________.
数字因数
所有字母的指数和
一个数
一个字母
注意的问题:
2.当式子分母中出现字母时不是单项式。
3.圆周率π是常数,不要看成字母。
4.当单项式的系数是带分数时,通常写成假分数。
5.单项式的系数应包括它前面的性质符号。
6.单项式次数是指所有字母的次数的和,与数字的次数没有关系。
7.单独的数字不含字母, 规定它的次数是零次.
1xy=xy、-1x=-x
2/a
×
3xy-xy
单项式注意:
1,分母含有字母的式子不属于单项式。因为单项式属于整式,而分母含有未知数的式子是分式。例如,1/x不是单项式。
2,单独的一个数字或字母也是单项式。例如,1和x^2y也是单项式。
3,单项式表示数与字母相乘时,通常把数写在前面。
如果一个单项式,只含有字母因数,如果是正数的单项式系数为1,如果是负数的单项式系数为-1。
如果一个单项式,只含有数字因数,那么它的次数为0。
单项式概念:
1.任意一个字母和数字的积的形式的代数式(除法中有:除以一个数等于乘这个数的倒数)。
2.单独一个字母或数字也叫单项式。
3.分母中不含字母(单项式是整式,而不是分式)
a,-5,1X,2XY,都是单项式,而0.5m+n,不是单项式。
4,0也是数字,也属于单项式。
5,有分数也属于单项式。
单项式的次数是指单项式中所有字母因数的指数和
这个名词是清代数学家李善兰译书时根据原词概念汉化的。
单项式是字母与数的乘积。
单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数。
单项式的系数:单项式中的数字因数。如:2xy的系数是2;-5zy 的系数是-5
字母t的指数是1,100t是一次单项式;在单项式vt中,字母v与t的指数的和是2,vt是二次单项式。
如:xy ,3,a z,ab,b ...... 都是单项式。
用运算符号把表示数的字母或数连接起来的式子叫代数式。
代数式不含有“≥”、“=”、“<”、“≠”符号等
单项式书写规则:数与字母相乘时,数在字母前;乘号可以省略为点或不写;除法的式子可以写成分数式;带分数与字母相乘,带分数要化为假分数
单项式是几次,就叫做几次单项式
字母不能在分母中(因为这样为分式,不为单项式)
“π”是特指的数,不是字母,读pài。
单项式书写格式:
1.数字写在字母的前面,应省略乘号。[5a 、16xy等]
2.π是常数,因此也可以作为系数。
3.若系数是带分数,要化成假分数。
4.当一个单项式的系数是1或-1时,“1”通常省略不写,如[(-1)ab ]写成[ -ab ]等。
5.在单项式中字母不可以做分母,分子可以。
6.单项式中系数不为0,否则单项无意义。
7.单独的数“0”的系数是零,次数也是零。
8.常数的系数是它本身,次数为零
单项式的计算:
单项式加减法则
单项式加减即合并同类项,也就是合并前各同类项系数的和,字母不变。
例如:3a+4a=7a,9a-2a=7a等单项式乘法法则
单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式
例如:3a·4a=12a^2单项式除法法则
同底数幂相除,底数不变,指数相减。
例如:9a^10÷3a^5=3a^5
多项式
若干个单项式的和组成的式子叫做多项式 。
例如:1/2a+3xy-4y
多项式的项:多项式中每个单项式叫做多项式的项 。
多项式的次数:这些单项式中的最高次数,就是这个多项式的次数。
多项式的常数项:多项式中的数字项,叫做多项式的常数项。
2
定义:几个__________.
常数项:多项式中_______________.
多项式的次数:_________________________.
项: 组成多项式中的_____________.
有几项,就叫做_________.
1.在确定多项式的项时,要连同它前面的符号,
2.一个多项式的次数最高项的次数是几,就说这个多项式是几次多项式。
3.在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念。
多项式
单项式的和
每一个单项式
几项式
不含字母的项
多项式中次数最高的项的次数。
注意的问题:
一、知识梳理:(不看课本,把下列空填写在横线上。若遇到不会的可翻阅课本)
1、由 或 的 组成的式子叫单项式。
单独的一个 或 也是单项式.
2、单项式中的 叫单项式的系数。所有 的指数的 叫单项式的次数。
3、几个单项式的 叫多项式。
4、式中的每个 叫多项式的项。(其中不含字母的项叫做 )
5、多项式中次数最 的项的次数叫多项式的次数。
6、多项式的每一项都包括它前面的 .
第一块复习
整式的加减
整式的加减
同类项
升降幂排列
整式的加减混合运算步骤(有括号先去括号)
1.找同类项,做好标记。
2.利用加法的交换律和结合律把同类项放在一起。
3.利用乘法分配律计算结果。
4.按要求按“升”或“降”幂排列。
找
搬
并
排
1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同。
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
“去括号,看符号。是‘+’号,不变号,是‘-’号,全变号”
一:去括号
二:计算
(按照先小括号,再中括号,最后大括号的顺序)
同类项的定义:
(两相同)
合并同类项概念:
_________________________.
合并同类项法则:
2._________________不变。
2._________________相同。
1.____相同,
字母
相同的字母的指数也
1.______相加减;
字母和字母的指数
系数
同类项
注意:几个常数项也是______
同类项。
(两无关)
2.与__________无关。
1.与____无关
系数
字母的位置
把多项式中的同类项合并成一项
掌握同类项的概念时注意:
1.判断几个单项式或项,是否是同类项,就要掌握两个条件:
①所含字母相同。
②相同字母的次数也相同.
2.同类项与系数无关,与字母排列的顺序也无关。
3.所有常数项都是同类项。
解:4x2 - 8x + 5-3x2 + 6x -4
~~~ ~~~
=(4x2-3x2)
= x2
合并同类项的步骤:
1、找出同类项
用不同的线标记出各组同类项,注意每一项的符号。
2、把同类项移在一起
用括号将同类项结合,括号间用加号连接。
3、合并同类项
系数相加,字母及字母的指数不变 。
(-8x+6x)
(5-4)
-2x
+1
2.合并多项式4x2-8x+5-3x2+6x-4中的同类项.
— ——
要记住呀!!
+ +
一找
二移
三并
2.若 与 是同类项,则m+n=___.
4.若 ,则m+n-p=______
5
4
3.若 与 的和是一个单项式,则 =___.
-4
1.下列各式中,是同类项的是:___________
① 与
② 与
③ 与
④ 与
⑤ 与
⑥-125与
③⑤⑥
同类项练习
1.下列各组中的两项是不是同类项?为什么?
(1) (2)
(3) (4)
(5) (6)
比一比,谁最棒
2.试一试,我能行
1、下列各组是同类项的是( )
A 2x3与3x2 B 12ax与8bx
C x4与a4 D π与-3
2、5x2y 和42xnym是同类项,则
m=______, n=________
3、 –xmy与45ynx3是同类项,则
m=_______. n=______
D
1
2
3
1
1.填空,并解释其中依据:
(1)
(2)
(3)
合并同类项:
定义:把多项式中的同类项合并成一项
法则:(1)系数:系数相加;
(2)字母:字母和字母的指数保持不变。
方法:逆用乘法分配律可以把同类项进行合并,合并时,把它们的系数相加作为新的系数,而字母部分不变。
3.合并下列多项式中的同类项:
(3)2a2-3ab+4b2+5ab-6b2
升、降幂排列
1.把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把多项式按这个字母降幂排列。
2.把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把多项式按这个字母升幂排列。
练习
下面的数中,哪些是单项式,哪些是多项式,哪些是整式?
-9,xyz,-x+3-xy,3.14+xy-5+2x
单项式: -9,xyz
多项式: -x+3-xy,3.14+xy-5+2x
整式: -9,xyz,-x+3-xy,3.14+xy-5+2x
去括号:
1-xy
-9xy-5xyz-9+7y
-(-1+xy)=
-9xy-(5xyz+9-7y)=
整式的加减的常见题型
1.实际问题
2.直接化简代入
3.条件求值
4.整体代入
求代数式的值
一、概念中的易错题
二、运算中的易错题
易错点总结:
注意:有多重括号的,一般先去小括号,再去中括号,最后再去大括号;
(先去括号)
(降幂排列)
(合并同类项,化简完成)
当x=-2时
(代入)
(代入时注意添上括号,乘号改回“×”)
单项式的定义
例1,下列各式子中,是单项式的有______________(填序号)
①、②、④、⑦
注意:1,单个的字母或数字也是单项式;
2,用加减号把数字或字母连接在一起
的式子不是单项式;
3,只用乘号把数字或字母连接在一起
的式子仍是单项式;
4,当式子中出现分母时,要留意分母里有
没有字母,有字母的就不是单项式,如
果分母没有字母的仍有可能是单项式
(注:“π”当作数字,而不是字母)
单项式的系数与次数
单项式
系数
次数
例2 指出下列单项式的系数和次数;
注意:1,字母的系数“1” 可以省略的,但不代表没有系
数(次数也是同样道理);
2,有分母的单项式,分母中的数字也是单项式系
数的一部分;
3,注意“π”不是字母,而是数字,属于系数的一
部分;
4,计算次数的时候并不是简单的见到指数就相
加,注意单项式的次数指的是字母的指数和;
多项式的项数与次数
例3 下列多项式次数为3的是( )
C
例4 请说出下列各多项式是几次几项式,并写出多项式的最高次项和常数项;
注意(1)多项式的次数不是所有项的次数的和,而是它的最高
次项次数;
(2)多项式的每一项都包含它前面的符号;
(3)再强调一次, “π”当作数字,而不是字母
书写格式中的易错点
例5 下列各个式子中,书写格式正确的是( )
1、代数式中用到乘法时,若是数字与数字乘,要用“×”
若是数字与字母乘,乘号通常写成”.”或省略不写,如
3×y应写成3·y或3y,且数字与字母相乘时,字母与
字母相乘,乘号通常写成“·”或省略不写。
2、带分数与字母相乘,要写成假分数
3、代数式中出现除法运算时,一般用分数写,即用分数
线代替除号。
4、系数一般写在字母的前面,且系数“1”往往会省略;
F
例6 王强班上有男生m人,女生比男生的一半多5人,王强班上的总人数(用m表示)为______人。
易错点:结果不进行化简,直接写
点拨:结果中有 它们是同类项,应合并以保证最后的结果最简.正确的写法是
同类项的判定与合并同类项的法则:
例1 判断下列各式是否是同类项?
点拨:对于(1)、(3),考察的是同类项的定义,所含字母相同,相同字母的指数也相同的称为同类项;所以(1)、(3)不是同类项;
对于(2),虽然好像它们的次数不一样,但其实它们都是常数项,所以,它们都是同类项;
对于(4),虽然它们的系数不同,字母的顺序也不同,但它依然满足同类项的定义,是同类项;
答:(2)、(4)是同类项,(1)(3)不是同类项;
例2 下列合并同类项的结果错误的有_______________.
①、②、③、④、⑤
注意:1,合并同类项的法则是把同类项的系数相加,字母和字母的次数不变;
2,合并同类项后也要注意书写格式;
3,如果两个同类项的系数互为相反数,那么合并同类项后,结果得____;
0
去括号中的易错题:
1,判断下列各式是否正确:
√
×
×
( )
( )
( )
×
( )
去括号时,1,注意括号外面的符号,括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不用变符号;括号前面是“—”号,把括号和它前面的“—”号去掉,括号里各项都改变符号。
2,注意外面有系数的,各项都要乘以那个系数;
例3 合并同类项:
小明的解法:
(1)错在把所有项都当作同类项了;
正确的解法:
例3 合并同类项:
小明的解法:
(2)错在把结合同类项时弄错了符号;
正确的解法:
总之,合并同类项现要找出式子中的同类项,并把它们写在一起,最后合并,注意同类项的系数是带符号的。
去括号中的易错题:
1、判断下列各式是否正确:
√
×
×
( )
( )
( )
×
( )
去括号时,1,注意括号外面的符号,括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不用变符号;括号前面是“—”号,把括号和它前面的“—”号去掉,括号里各项都改变符号。
2,注意外面有系数的,各项都要乘以那个系数;
练一练:
1,化简下列各式:
整式的加减一般步骤是(1)如果有括号就先去括号,(2)然后再合并同类项.
多重括号化简的易错题
注意:有多重括号的,一般先去小括号,再去中括号,最后再去大括号;
化简求值中的易错题:
(先去括号)
(降幂排列)
(合并同类项,化简完成)
当x=-2时
(代入)
(代入时注意添上括号,乘号改回“×”)
1.去掉下列各式中的括号。
(1)8m-(3n+5)
(2)n-4(3-2m)
(3)2(a-2b)-3(2m-n)
=8m-3n-5
=n-12+8m
=2a-4b-6m+3n
2.化简:
-(3x-2y+z)-[5x-x+2y-z-3x]
解:原式=
-(3x-2y+z)-[5x-(x-2y+z)-3x]
=-(3x-2y+z)-[x+2y-z]
=-(3x-2y+z)-[(5x-x-3x)+2y-z]
=-3x+2y-z-x-2y+z
=(-3x-x)+(2y-2y)+(-z+z)
=-4x
“A+2B”类型的易错题:
例1 若多项式 计算多项式A-2B;
注意:列式时要先加上括号,再去括号;
例2 一个多项式A加上 得 ,求这个多项式A?
注意:我们在移项的时候是整体移项,不要漏了添上括号;
2,实际问题中的易错题:
例1 某种手机卡的市话费上次已按原收费标准降低了m元/分钟,现在再次下调20%,使收费标准为n元/分钟,那么原收费标准为 ( ).
B
点拨:为了弄清各数之间的关系,我们可以借助方程来求解.假设原收费标准为每分钟x元,可得:
解得 .应选B.
例2 若长方形的一边长为a+2b,另一边长比它的3倍少a-b,求这个长方形的周长?
分析:如果直接列式的话,非常麻烦,我们可以先求出另一边长,再求周长,这样就比较容易求出答案;
解:一边长为:a+2b;
另一边长为:3(a+2b)-(a-b)
=3a+6b-a+b
=3a-a+6b+b
=2a+7b;
周长为:2(a+2b+2a+7b)
=2(a+2a+2b+7b)
=2(3a+9b)
=6a+18b;
答:长方形的周长为6a+18b
从错误中吸取教训,
从失败中取得进步,
完善完整知识网络,
我将会成为最棒的!
第n个图案中有地砖 块.
重点题,考试必考
求当x= 时,多项式
的值。
解:原式=
=
=
把x= 带入 中,得
∴ 原式=5
补充例题:
a
0
b
已知数a,b在数轴上的位置如图所示
化简下列式子:
∴原式=-a-2[-(a+b)]-3(b-a)
解:由题意知:a<0,b>0且|a|>|b|
=-a+2[a+b]-3b+3a
=-a+2a+2b-3b+3a
=(-a+2a+3a)+(2b-3b)
=4a-b
当x=1时, 则当x=-1时,
解:将x=1代入 中得:
a+b-2=3
∴ a+b=5;
当x=-1时
=-a-b-2
=-(a+b)-2
=-7
=-5-2
若-5a3bm+1与8an+1b2是同类项,求(m-n)100的值。
解:由同类项的定义知:m+1=2,n+1=3;解得m=1,n=2
∴(m-n)100=(1-2)100=(-1)100=1
答:当m=1,n=2时,(m-n)100=1。
评析:例1要注意同类项概念的应用;例2要注意几位数的表示方法。如:578=5×100+7×10+8。
如果一个两位数的个位数是十位数的4倍,那么这个两位数一定是7的倍数。请说明理由。
解:设两位数的十位数字是x,则它的个位数字是4x。
∴这个两位数可表示为:10x+4x=14x,
∵14x是7的倍数,故这个两位数是7的倍数。
已知多项式A= ,B= ,C=
求 2A-5B+3C=
解:原式=
=
=
=
如果关于x的多项式 的值与x
无关,则a的取值为_____.
解:原式=
由题意知,则:
6a-6=0
∴a=1
1
如果关于x,y的多项式 的差
不含有二次项,求 的值。
解:原式=
由题意知,则:
m-3=0
2+2n=0
∴m=3,n=-1;
∴ = =-1
1.指出下各式的关系(相等、相反数、不确定):
(1) a-b与b-a
(2) -a-b与-(b-a)
(3) –(a-b)与b-a
(4) –(a-b)与b-a
2.
补充两题:
同课章节目录
