人教版七年级上册 2整式的加减 复习课件(共56张PPT)
文档属性
| 名称 | 人教版七年级上册 2整式的加减 复习课件(共56张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-07 17:40:12 | ||
图片预览











文档简介
(共56张PPT)
第二章:整式的加减
章节复习
一、整式的有关概念
1、代数式:象
等式子,称为代数式。
注意:代数式的书写要求:
以上代数式中,那些符合代数式的书写要求?
特别地:单独的一个数或字母也是代数式
练习:
2、代数式的值:
用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果,叫做代数式的值
如果代数式5a+3b的值为- 4, 求代数式 2(a+b)+4(2a+b)的值.
解: 2(a+b)+4(2a+b)
=2a+2b+8a+4b
=10a+6b
=2(5a+3b)
当5a+3b=-4时
原式 =2×(-4)
=-8
练习:
3、单项式:
4、单项式的系数:
单项式中的数字因数。
数与字母乘积组成的代数式叫单项式。单独一个数或字母也是单项式。
练一练:
几个单项式的和叫多项式。
7、多项式的项及次数:组成多项式中的单项式叫多项式的项,多项式中次数最高项的次数叫多项式的次数。
5、单项式的次数:
单项式中所有的字母的指数和。
练习:指出下列单项式的系数与指数各是多少。a , , , π ,
6、多项式:
练习:下面多项式是由那些单项式组成?
特别注意,多项式的次数不是组成多项式的所有字母指数和!!!
练习:下面多项式是几次几项式?指出它的各项
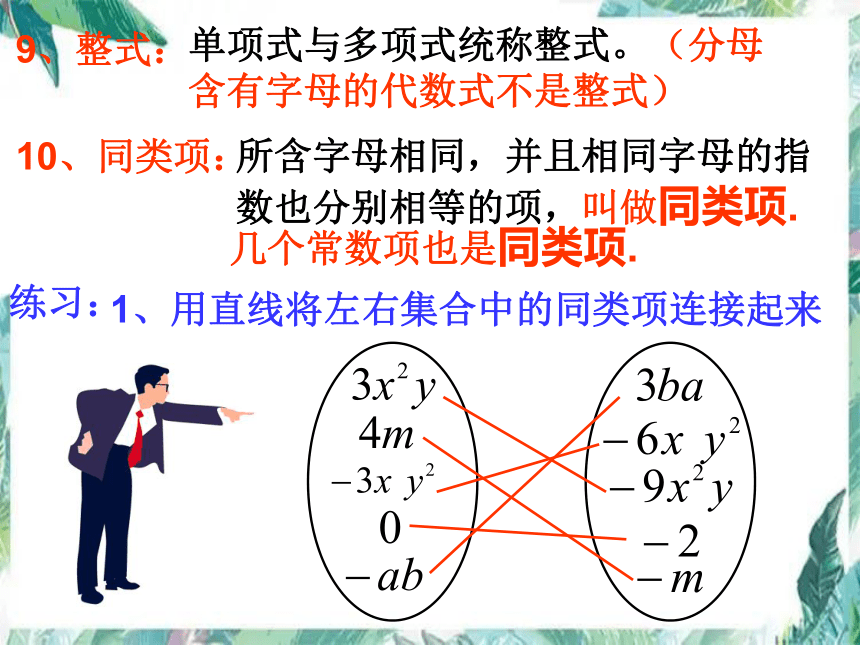
单项式与多项式统称整式。(分母含有字母的代数式不是整式)
10、同类项:
9、整式:
所含字母相同,并且相同字母的指数也分别相等的项,叫做同类项.
练习:
1、用直线将左右集合中的同类项连接起来
几个常数项也是同类项.
练习:2、若 与 是同类项,则m= ,n= 。
二、整式的加减法
1、同类项的合并法则:
把同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变。
2、去括号法则:
去掉前面带“—”的括号,括号内的各项都改变符号。
去掉前面带“+”的括号,括号内的各项都不变符号。
7
1
基本步骤:去括号,合并同类项。
3、整式的加减:
练习:
2、求整式 与 的差
解:( )-( )
=
=
a
0
b
已知数a,b在数轴上的位置如图所示
化简下列式子:
整式与绝对值
填写下表,并观察下列两个代数式的值的变化情况
n 1 2 3 4 5 6 7 8
16
11
21
26
31
36
41
46
1
4
9
16
25
36
49
64
思考
(1)随着n的值逐渐变大,两个代数式的值如何变化?
(2)估计一下,哪个代数式的值先超过100。
5n+6
解:(1) m×m= m2
电教室里的座位的排数是m,用代数式表示:
(1)若每排座位数是排数的 倍,则电教室里共有多少个座位?
(2)若第一排的座位数是a,并且后一排总比前一排的座位数多1个,则电教室里第m排有多少个座位?
(2) a+m-1
a
+1
a
a +1
+1
a +1 +1
+ …+1
m-1
…
第1排
第2排
第3排
第m排
…
{
练一练
探索数据排列的规律
根据下列已知数,寻找规律并填空:
(1) 1 ,3 ,5 , 7 ,____ , ____ , … … ____;
9
11
(3) 2 ,5 ,10 ,17 ,____ , ____ , … … ____;
26
37
2n-1
n2+ 1
(2) 3, 8, 13,18,______ , ______ , … … _______;
第n个数
23
28
3+5n
第n个数
n
3n
n2
1,2,3,4,5……
3,6,9,12,15……
1,4,9,16,25……
3,7,11,15,19,……
第n个数字是多少呢?
4n-1
这些等式反映了自然数间的某种规律,设n表示自然数,用关于n的等式把这种规律表示出来:
______________________
观察下列等式:
× + =
1
3
22
n
n+2
(n+1)2
第n个数
1
× + =
× + =
× + =
2
3
4
4
5
6
1
1
1
32
42
52
× +1= 2
…………
n
(n+2)
(n+1)
(2)照这样的规律搭下去,搭n个这样的三角形需要多少根火柴棒?
(1)填写下表:
三角形个数 1 2 3 4 5
火柴棒根数
5
11
3
9
7
(2n+1)根
答:搭n个这样的三角形需要火柴棒
10
100
21
201
用火柴棒按下图的方式搭三角形
探索图形排列的规律
游戏: (见下图)
搭第一个正方形需要4根火柴棒。
(1)搭一搭,填一填:
正方形个数
火柴棒根数 1 2 3 4 5
4
7
10
13
16
(2)搭10个这样的正方形需要 _ 根火柴棒。
31
(3)搭100个这样的正方形需要多少根火柴棒?你是怎样得到的?
第一个正方形用4根,每增加一个正方形增加3根,那么搭100个正方形就需要火柴棒 4+3×(100-1)根。
…
100个正方形
…
100个正方形
把搭第一个正方形的方法看做是先搭1根再增加3根,那么搭100个正方形就需要1+3×100根。
…
100个正方形
…
100个正方形
把每一个正方形看成是用4根搭成的,然后再减去多算的根数,将得到4×100-(100-1)根.
…
100个正方形
…
100个正方形
上面的一排和下面的一排各用了100根,竖直方向用了100+1根,共用了100+100+(100+1)根.
…
100个正方形
…
100个正方形
(4)如果用x表示所搭正方形的个数,那么搭x个这样的正方形需要多少根火柴棒?
(5)根据你的算法,搭200个这样的正方形需要__根火柴棒。
601
(3)搭100个这样的正方形需要多少根柴棒?你是怎样得到的?
(301根)
(3x+1)根
(2)第 n 个图形需要多少根火柴棒?
①5n+2 ②7+5(n-1) ③7n-2(n-1) ④3n+2(n+1) ……
① ② ③
图形编号 ① ② ③ ④ ⑤ ⑥
火柴棒根数
(1)填写下表:
7
12
17
22
27
32
① 对折次数与所得层数的变化关系表:
对折次数 1 2 3 4 … n
所得层数
② 对折次数与所得折痕数的变化关系表:
对折次数 1 2 3 4 … n
折痕条数
将一张普通的报纸对折,可得到一条折痕。继续对折,对折时每次折痕与上次的折痕保持平行。连续对折4次后,可以得到几层纸、几条折痕?如果对折10次呢?对折n次呢?
2
4
8
16
1
3
7
15
2n
2n-1
折一折 议一议
用棋子按下面的方式摆出正方形:
1
2
3
(1)按图示规律填写下表:
棋子个数
6
5
4
3
2
1
图形编号
(2)按照这种方式摆下去,摆第n个正方形需要 个棋子?
练习2
用棋子按下面的方式摆出正方形:
1
2
3
(1)按图示规律填写下表:
图形编号 1 2 3 4 5 6
棋子个数
(2)按照这种方式摆下去,摆第n个正方形需要 个棋子?
4n
4
8
12
16
20
24
练习2
摆第一个图形用____枚棋子,摆第二个图形用____枚棋子,摆第三个图形用____枚棋子。摆第n个图形用_____枚棋子,摆第100个图形用_____枚棋子.
6
9
3n
300
3
练习3
1
2
3
4
n
用棋子摆成下面的“小屋子”:
摆第 1 个“小屋子”需要 5 枚 棋子,
摆第 2 个“小屋子”需要 枚 棋子,
摆第 3 个“小屋子”需要 枚 棋子,
11
17
练习4
用棋子摆成下面的“小屋子”:
(1) 摆第 10 个这样的“小屋子”需要 枚 棋子,
(2) 摆第 n 个这样的“小屋子”需要 枚 棋子.
第n 个屋子 1 2 3 4 … 10 … n
棋子的个数 5 11 17 … …
23
59
6n-1
小结:
像这样通过对现象的观察、分析,从特殊到一般地探索这种现象规律的思想方法称为“归纳”,用归纳的方法进行探索,能够帮助我们解决许多实际问题!
联体长方形的摆法:(填空)
1. 如图,摆N个这样联体图形需 根火柴棒。
2 如图,摆N个这样联体图形需 根火柴棒。
练习1
3、如图,摆N个这样联体图形需 根火柴棒。
3n+1
7n+3
5n+2
( )
( )
( )
第二章:整式的加减
章节复习
一、整式的有关概念
1、代数式:象
等式子,称为代数式。
注意:代数式的书写要求:
以上代数式中,那些符合代数式的书写要求?
特别地:单独的一个数或字母也是代数式
练习:
2、代数式的值:
用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果,叫做代数式的值
如果代数式5a+3b的值为- 4, 求代数式 2(a+b)+4(2a+b)的值.
解: 2(a+b)+4(2a+b)
=2a+2b+8a+4b
=10a+6b
=2(5a+3b)
当5a+3b=-4时
原式 =2×(-4)
=-8
练习:
3、单项式:
4、单项式的系数:
单项式中的数字因数。
数与字母乘积组成的代数式叫单项式。单独一个数或字母也是单项式。
练一练:
几个单项式的和叫多项式。
7、多项式的项及次数:组成多项式中的单项式叫多项式的项,多项式中次数最高项的次数叫多项式的次数。
5、单项式的次数:
单项式中所有的字母的指数和。
练习:指出下列单项式的系数与指数各是多少。a , , , π ,
6、多项式:
练习:下面多项式是由那些单项式组成?
特别注意,多项式的次数不是组成多项式的所有字母指数和!!!
练习:下面多项式是几次几项式?指出它的各项
单项式与多项式统称整式。(分母含有字母的代数式不是整式)
10、同类项:
9、整式:
所含字母相同,并且相同字母的指数也分别相等的项,叫做同类项.
练习:
1、用直线将左右集合中的同类项连接起来
几个常数项也是同类项.
练习:2、若 与 是同类项,则m= ,n= 。
二、整式的加减法
1、同类项的合并法则:
把同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变。
2、去括号法则:
去掉前面带“—”的括号,括号内的各项都改变符号。
去掉前面带“+”的括号,括号内的各项都不变符号。
7
1
基本步骤:去括号,合并同类项。
3、整式的加减:
练习:
2、求整式 与 的差
解:( )-( )
=
=
a
0
b
已知数a,b在数轴上的位置如图所示
化简下列式子:
整式与绝对值
填写下表,并观察下列两个代数式的值的变化情况
n 1 2 3 4 5 6 7 8
16
11
21
26
31
36
41
46
1
4
9
16
25
36
49
64
思考
(1)随着n的值逐渐变大,两个代数式的值如何变化?
(2)估计一下,哪个代数式的值先超过100。
5n+6
解:(1) m×m= m2
电教室里的座位的排数是m,用代数式表示:
(1)若每排座位数是排数的 倍,则电教室里共有多少个座位?
(2)若第一排的座位数是a,并且后一排总比前一排的座位数多1个,则电教室里第m排有多少个座位?
(2) a+m-1
a
+1
a
a +1
+1
a +1 +1
+ …+1
m-1
…
第1排
第2排
第3排
第m排
…
{
练一练
探索数据排列的规律
根据下列已知数,寻找规律并填空:
(1) 1 ,3 ,5 , 7 ,____ , ____ , … … ____;
9
11
(3) 2 ,5 ,10 ,17 ,____ , ____ , … … ____;
26
37
2n-1
n2+ 1
(2) 3, 8, 13,18,______ , ______ , … … _______;
第n个数
23
28
3+5n
第n个数
n
3n
n2
1,2,3,4,5……
3,6,9,12,15……
1,4,9,16,25……
3,7,11,15,19,……
第n个数字是多少呢?
4n-1
这些等式反映了自然数间的某种规律,设n表示自然数,用关于n的等式把这种规律表示出来:
______________________
观察下列等式:
× + =
1
3
22
n
n+2
(n+1)2
第n个数
1
× + =
× + =
× + =
2
3
4
4
5
6
1
1
1
32
42
52
× +1= 2
…………
n
(n+2)
(n+1)
(2)照这样的规律搭下去,搭n个这样的三角形需要多少根火柴棒?
(1)填写下表:
三角形个数 1 2 3 4 5
火柴棒根数
5
11
3
9
7
(2n+1)根
答:搭n个这样的三角形需要火柴棒
10
100
21
201
用火柴棒按下图的方式搭三角形
探索图形排列的规律
游戏: (见下图)
搭第一个正方形需要4根火柴棒。
(1)搭一搭,填一填:
正方形个数
火柴棒根数 1 2 3 4 5
4
7
10
13
16
(2)搭10个这样的正方形需要 _ 根火柴棒。
31
(3)搭100个这样的正方形需要多少根火柴棒?你是怎样得到的?
第一个正方形用4根,每增加一个正方形增加3根,那么搭100个正方形就需要火柴棒 4+3×(100-1)根。
…
100个正方形
…
100个正方形
把搭第一个正方形的方法看做是先搭1根再增加3根,那么搭100个正方形就需要1+3×100根。
…
100个正方形
…
100个正方形
把每一个正方形看成是用4根搭成的,然后再减去多算的根数,将得到4×100-(100-1)根.
…
100个正方形
…
100个正方形
上面的一排和下面的一排各用了100根,竖直方向用了100+1根,共用了100+100+(100+1)根.
…
100个正方形
…
100个正方形
(4)如果用x表示所搭正方形的个数,那么搭x个这样的正方形需要多少根火柴棒?
(5)根据你的算法,搭200个这样的正方形需要__根火柴棒。
601
(3)搭100个这样的正方形需要多少根柴棒?你是怎样得到的?
(301根)
(3x+1)根
(2)第 n 个图形需要多少根火柴棒?
①5n+2 ②7+5(n-1) ③7n-2(n-1) ④3n+2(n+1) ……
① ② ③
图形编号 ① ② ③ ④ ⑤ ⑥
火柴棒根数
(1)填写下表:
7
12
17
22
27
32
① 对折次数与所得层数的变化关系表:
对折次数 1 2 3 4 … n
所得层数
② 对折次数与所得折痕数的变化关系表:
对折次数 1 2 3 4 … n
折痕条数
将一张普通的报纸对折,可得到一条折痕。继续对折,对折时每次折痕与上次的折痕保持平行。连续对折4次后,可以得到几层纸、几条折痕?如果对折10次呢?对折n次呢?
2
4
8
16
1
3
7
15
2n
2n-1
折一折 议一议
用棋子按下面的方式摆出正方形:
1
2
3
(1)按图示规律填写下表:
棋子个数
6
5
4
3
2
1
图形编号
(2)按照这种方式摆下去,摆第n个正方形需要 个棋子?
练习2
用棋子按下面的方式摆出正方形:
1
2
3
(1)按图示规律填写下表:
图形编号 1 2 3 4 5 6
棋子个数
(2)按照这种方式摆下去,摆第n个正方形需要 个棋子?
4n
4
8
12
16
20
24
练习2
摆第一个图形用____枚棋子,摆第二个图形用____枚棋子,摆第三个图形用____枚棋子。摆第n个图形用_____枚棋子,摆第100个图形用_____枚棋子.
6
9
3n
300
3
练习3
1
2
3
4
n
用棋子摆成下面的“小屋子”:
摆第 1 个“小屋子”需要 5 枚 棋子,
摆第 2 个“小屋子”需要 枚 棋子,
摆第 3 个“小屋子”需要 枚 棋子,
11
17
练习4
用棋子摆成下面的“小屋子”:
(1) 摆第 10 个这样的“小屋子”需要 枚 棋子,
(2) 摆第 n 个这样的“小屋子”需要 枚 棋子.
第n 个屋子 1 2 3 4 … 10 … n
棋子的个数 5 11 17 … …
23
59
6n-1
小结:
像这样通过对现象的观察、分析,从特殊到一般地探索这种现象规律的思想方法称为“归纳”,用归纳的方法进行探索,能够帮助我们解决许多实际问题!
联体长方形的摆法:(填空)
1. 如图,摆N个这样联体图形需 根火柴棒。
2 如图,摆N个这样联体图形需 根火柴棒。
练习1
3、如图,摆N个这样联体图形需 根火柴棒。
3n+1
7n+3
5n+2
( )
( )
( )
同课章节目录
