人教版八年级上册 全等三角形专题复习课件(共17张PPT)
文档属性
| 名称 | 人教版八年级上册 全等三角形专题复习课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 320.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-07 16:01:51 | ||
图片预览




文档简介
(共17张PPT)
《全等三角形》专题复习
八年级—人教版—数学—第十二章
学习目标
1.能综合运用等腰直角三角形、全等三角形的性质与判定进行计算和证明;
2.能在图形的构造过程中感受图形之间的变化和联系,体验“变”中“不变”的相对关系.
题1 如图,已知△ABC中,∠ACB=90°,∠B=45°,AC=2,则BC= ;
2
一、以退为进
∠A=90°-∠B=45°
∠A=∠B
BC=AC=2
2
?
∠ACB=90°,∠B=45°
分析:
45°
题2 如图,已知△ABC中,∠ACB=90°,
AD=CE,CD=BE
△CAD与△BCE
AD=CE,CD=BE
∠ADC=∠CEB=90°
AC=BC
∠1=∠3
∠2+∠3=90°
∠1+∠2=90°
E
D
l
2
3
1
过点C在△ABC的外部作直线l ,
AC=BC,
分别过点B、A作BE⊥l于E,AD⊥l于D.
则相等的线段有______________.
}
}
一、以退为进
分析:
∠ADC=∠CEB=90°
△CAD≌△BCE(AAS)
E
B
A
C
D
l
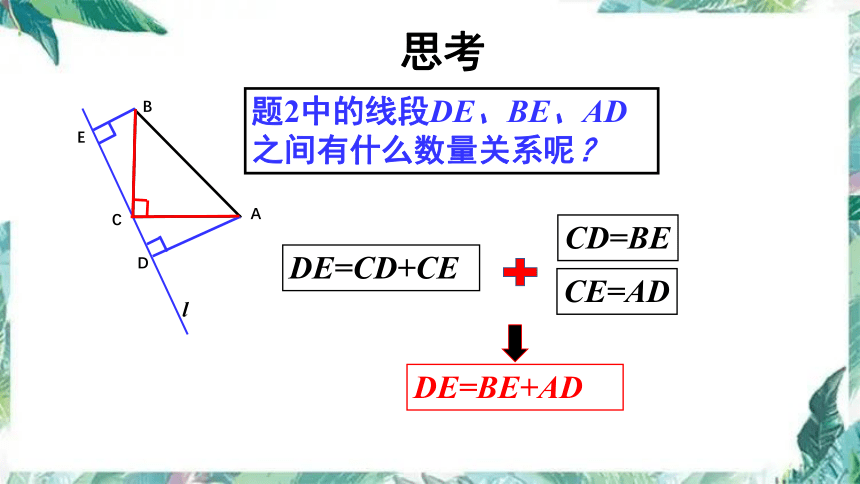
DE=BE+AD
题2中的线段DE、BE、AD之间有什么数量关系呢?
思考
DE=CD+CE
CD=BE
CE=AD
B
A
C
l
B
A
C
E
D
l
E
D
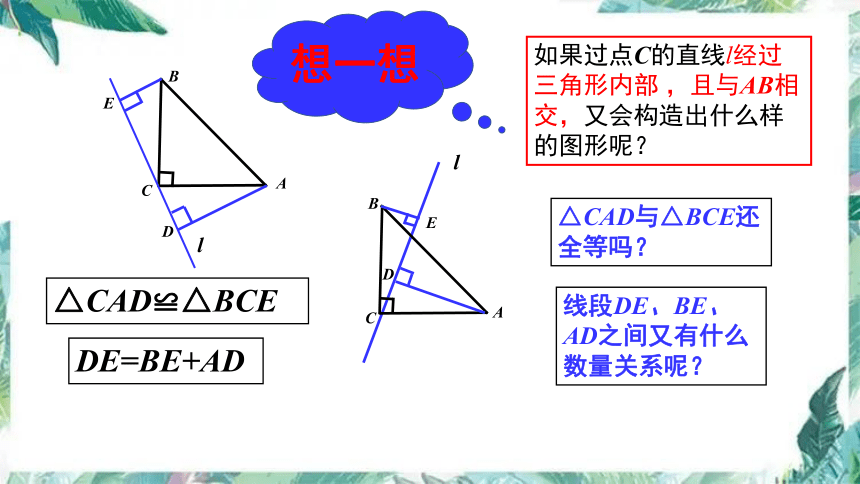
△CAD≌△BCE
△CAD与△BCE还全等吗?
线段DE、BE、AD之间又有什么数量关系呢?
DE=BE+AD
如果过点C的直线l经过三角形内部 ,且与AB相交,又会构造出什么样的图形呢?
想一想
二、以小见大
△BCE≌△CAD
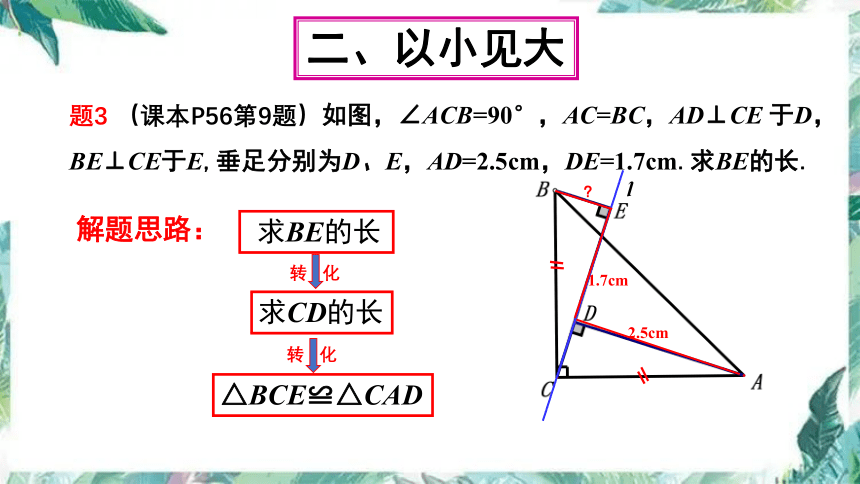
求CD的长
转 化
2.5cm
1.7cm
?
求BE的长
解题思路:
转 化
题3 (课本P56第9题)如图,∠ACB=90°,AC=BC,AD⊥CE 于D, BE⊥CE于E,垂足分别为D、E,AD=2.5cm,DE=1.7cm.求BE的长.
l
△BCE≌△CAD(AAS)
∠BEC=∠CDA=90°
∠3=∠1
BC=AC
∠1+∠2=90 °
∠2+∠3=90 °
?
1.7cm
2.5cm
3
2
1
二、以小见大
题3 (课本P56第9题)如图,∠ACB=90°,AC=BC,AD⊥CE于D, BE⊥CE于E,垂足分别为D、E,AD=2.5cm,DE=1.7cm.求BE的长.
}
}
分析:
1
2
3
解:∵AD⊥CE, BE⊥CE
∴∠BEC=∠CDA=90°
∴∠1+∠2=90°
又∵ ∠2+∠3=∠ACB=90°
∴ ∠3=∠1
在△BCE与△CAD 中
∴ △BCE≌△CAD(AAS)
∠BEC=∠CDA
∠3=∠1
BC=AC
∴BE=CD CE=AD
∵ AD=2.5cm,DE=1.7cm
∴ BE=CD=CE-DE
=AD-DE
=0.8cm
题3 (课本P56第9题)如图,∠ACB=90°AC=BC,AD⊥CE于D, BE⊥CE于E,垂足分别为D、E,AD=2.5cm,DE=1.7cm.求BE的长.
1.7cm
2.5cm
?
{
二、以小见大
学习启示
虽然直线l 的位置不同,但△BCE与△CAD始终保持全等
结论:直线l在绕点C运动过程中,虽然△BCE与△CAD大小形状在改变,但它们始终保持全等.
观察:直线l在绕点C运动过程中,△BCE与△CAD的变化及之间的关系。
学习启示
三、学以致用
题4 如图,将正方形OABC放在平面直角坐标系中,
O是原点,A的坐标是(1,2), 求点C的坐标.
A
B
C
O
x
y
D
E
分析:
求点C的坐标
求线段CE、OE的长
转 化
证△OEC≌△ADO
转 化
2
1
?
?
(1,2)
三、学以致用
题4 如图,将正方形OABC放在平面直角坐标系中,
O是原点,A的坐标是(1,2), 求点C的坐标.
A
B
C
O
x
y
D
E
解:
过点A作AD⊥x轴于D
∠CEO=∠ADO=90°
∴∠1+∠2=90°
∵ 四边形OABC是正方形
∴CO=AO,∠AOC=90°
∴AD=2,OD=1
∴ ∠2+∠3=90°
∴ ∠1=∠3
∠1=∠3
∴ 在△OEC 与△ADO中
{
∠CEO=∠ADO
CO=AO
∴ △OEC ≌△ADO(AAS)
∴ OE=AD=2,CE=OD=1
∴点C的坐标为(-2,1)
3
1
2
过点C作CE⊥x轴于E
2
1
点的坐标
线段的长
证全等
基 本 图 形
拓 展
延 伸
题2
题3
题4
条件:∠ADC=∠BEC=∠BCA=90°,且D、C、E在同一直线上,AC=BC.
结论:△BCE≌△CAD.
归纳
四、课堂小结
构造
变
变
基本图形
(实质)
会在图形的构造过程中看到图形的变化和联系
会在变化图形中找到不变的基本图形关系
会利用全等这个工具得到线段之间的数量关系
五、课后作业
1.(课本第56页第10题)如图的三角形纸片中,
AB=8cm,BC=6cm,AC=5cm.沿点B的直线折叠
这个三角形,使点C落在AB边上的点E处,折痕
为BD.求△AED的周长.
2.(课本第56页第13题)证明:如果两个三角形有两条边
和其中一边上的中线分别相等,那么这两个三角形全等.
谢 谢
《全等三角形》专题复习
八年级—人教版—数学—第十二章
学习目标
1.能综合运用等腰直角三角形、全等三角形的性质与判定进行计算和证明;
2.能在图形的构造过程中感受图形之间的变化和联系,体验“变”中“不变”的相对关系.
题1 如图,已知△ABC中,∠ACB=90°,∠B=45°,AC=2,则BC= ;
2
一、以退为进
∠A=90°-∠B=45°
∠A=∠B
BC=AC=2
2
?
∠ACB=90°,∠B=45°
分析:
45°
题2 如图,已知△ABC中,∠ACB=90°,
AD=CE,CD=BE
△CAD与△BCE
AD=CE,CD=BE
∠ADC=∠CEB=90°
AC=BC
∠1=∠3
∠2+∠3=90°
∠1+∠2=90°
E
D
l
2
3
1
过点C在△ABC的外部作直线l ,
AC=BC,
分别过点B、A作BE⊥l于E,AD⊥l于D.
则相等的线段有______________.
}
}
一、以退为进
分析:
∠ADC=∠CEB=90°
△CAD≌△BCE(AAS)
E
B
A
C
D
l
DE=BE+AD
题2中的线段DE、BE、AD之间有什么数量关系呢?
思考
DE=CD+CE
CD=BE
CE=AD
B
A
C
l
B
A
C
E
D
l
E
D
△CAD≌△BCE
△CAD与△BCE还全等吗?
线段DE、BE、AD之间又有什么数量关系呢?
DE=BE+AD
如果过点C的直线l经过三角形内部 ,且与AB相交,又会构造出什么样的图形呢?
想一想
二、以小见大
△BCE≌△CAD
求CD的长
转 化
2.5cm
1.7cm
?
求BE的长
解题思路:
转 化
题3 (课本P56第9题)如图,∠ACB=90°,AC=BC,AD⊥CE 于D, BE⊥CE于E,垂足分别为D、E,AD=2.5cm,DE=1.7cm.求BE的长.
l
△BCE≌△CAD(AAS)
∠BEC=∠CDA=90°
∠3=∠1
BC=AC
∠1+∠2=90 °
∠2+∠3=90 °
?
1.7cm
2.5cm
3
2
1
二、以小见大
题3 (课本P56第9题)如图,∠ACB=90°,AC=BC,AD⊥CE于D, BE⊥CE于E,垂足分别为D、E,AD=2.5cm,DE=1.7cm.求BE的长.
}
}
分析:
1
2
3
解:∵AD⊥CE, BE⊥CE
∴∠BEC=∠CDA=90°
∴∠1+∠2=90°
又∵ ∠2+∠3=∠ACB=90°
∴ ∠3=∠1
在△BCE与△CAD 中
∴ △BCE≌△CAD(AAS)
∠BEC=∠CDA
∠3=∠1
BC=AC
∴BE=CD CE=AD
∵ AD=2.5cm,DE=1.7cm
∴ BE=CD=CE-DE
=AD-DE
=0.8cm
题3 (课本P56第9题)如图,∠ACB=90°AC=BC,AD⊥CE于D, BE⊥CE于E,垂足分别为D、E,AD=2.5cm,DE=1.7cm.求BE的长.
1.7cm
2.5cm
?
{
二、以小见大
学习启示
虽然直线l 的位置不同,但△BCE与△CAD始终保持全等
结论:直线l在绕点C运动过程中,虽然△BCE与△CAD大小形状在改变,但它们始终保持全等.
观察:直线l在绕点C运动过程中,△BCE与△CAD的变化及之间的关系。
学习启示
三、学以致用
题4 如图,将正方形OABC放在平面直角坐标系中,
O是原点,A的坐标是(1,2), 求点C的坐标.
A
B
C
O
x
y
D
E
分析:
求点C的坐标
求线段CE、OE的长
转 化
证△OEC≌△ADO
转 化
2
1
?
?
(1,2)
三、学以致用
题4 如图,将正方形OABC放在平面直角坐标系中,
O是原点,A的坐标是(1,2), 求点C的坐标.
A
B
C
O
x
y
D
E
解:
过点A作AD⊥x轴于D
∠CEO=∠ADO=90°
∴∠1+∠2=90°
∵ 四边形OABC是正方形
∴CO=AO,∠AOC=90°
∴AD=2,OD=1
∴ ∠2+∠3=90°
∴ ∠1=∠3
∠1=∠3
∴ 在△OEC 与△ADO中
{
∠CEO=∠ADO
CO=AO
∴ △OEC ≌△ADO(AAS)
∴ OE=AD=2,CE=OD=1
∴点C的坐标为(-2,1)
3
1
2
过点C作CE⊥x轴于E
2
1
点的坐标
线段的长
证全等
基 本 图 形
拓 展
延 伸
题2
题3
题4
条件:∠ADC=∠BEC=∠BCA=90°,且D、C、E在同一直线上,AC=BC.
结论:△BCE≌△CAD.
归纳
四、课堂小结
构造
变
变
基本图形
(实质)
会在图形的构造过程中看到图形的变化和联系
会在变化图形中找到不变的基本图形关系
会利用全等这个工具得到线段之间的数量关系
五、课后作业
1.(课本第56页第10题)如图的三角形纸片中,
AB=8cm,BC=6cm,AC=5cm.沿点B的直线折叠
这个三角形,使点C落在AB边上的点E处,折痕
为BD.求△AED的周长.
2.(课本第56页第13题)证明:如果两个三角形有两条边
和其中一边上的中线分别相等,那么这两个三角形全等.
谢 谢
