沪科版八年级上册15.3.3等腰三角形的判定( 第3课时)课件(共25张PPT)
文档属性
| 名称 | 沪科版八年级上册15.3.3等腰三角形的判定( 第3课时)课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 631.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
第15章 轴对称图形与等腰三角形
15.3等腰三角形
第3课时 等腰三角形的判定
1.掌握等腰三角形的判定定理,运用定理进行论证和证明;(重点)
2.掌握等边三角形的判定定理.(重点)
3.掌握含30°角的直角三角形的性质并解决有关问题.(难点)
学习目标
等腰三角形有哪些性质?
1.等腰三角形的两底角相等.
(简写成 “等边对等角”)
A
B
C
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
知识回顾
2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.( 简写成“三线合一” )
A
B
C
D
∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(三线合一)
∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(三线合一)
∵AB=AC, AD⊥BC (已知)
∴ BD=CD ,∠BAD=∠CAD (三线合一)
知识讲解
在△ABC中,AB=AC,倘若不留神,它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C,请问,有没有办法把原来的等腰三角形画出来?
A
B
C
A
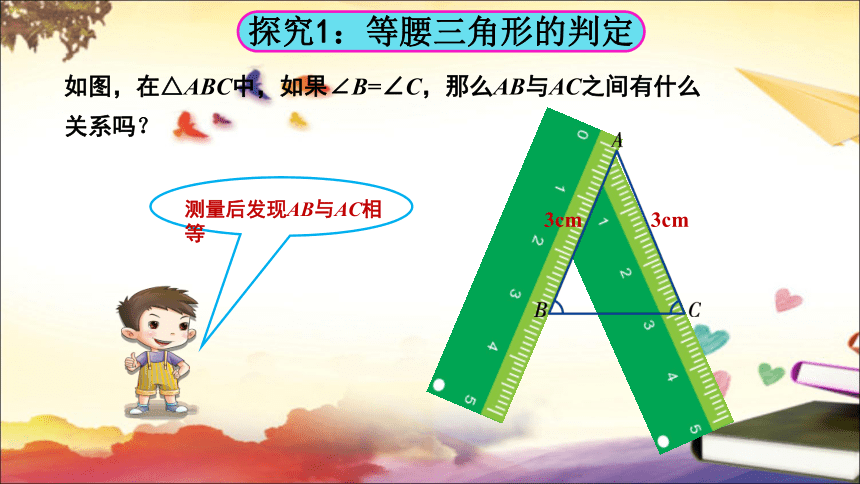
如图,在△ABC中,如果∠B=∠C,那么AB与AC之间有什么关系吗?
3cm
3cm
测量后发现AB与AC相等
探究1:等腰三角形的判定
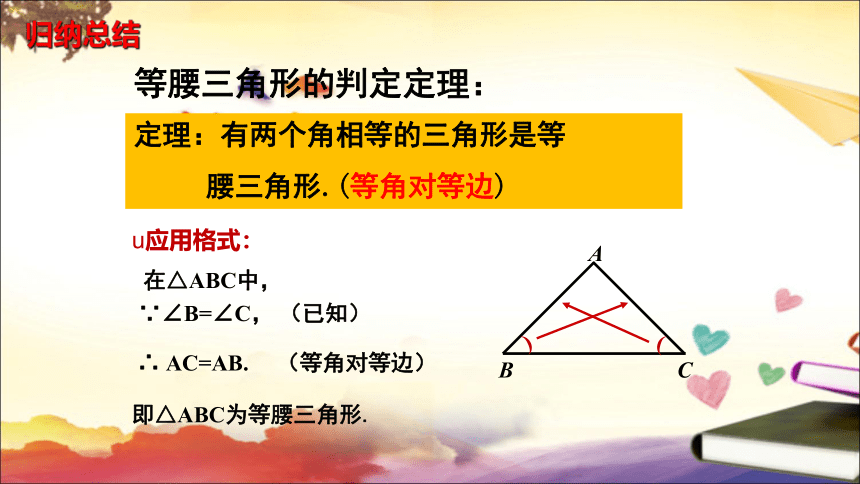
定理:有两个角相等的三角形是等
腰三角形.(等角对等边)
等腰三角形的判定定理:
归纳总结
应用格式:
在△ABC中,
∵∠B=∠C, (已知)
∴ AC=AB. (等角对等边)
即△ABC为等腰三角形.
B
C
A
(
(
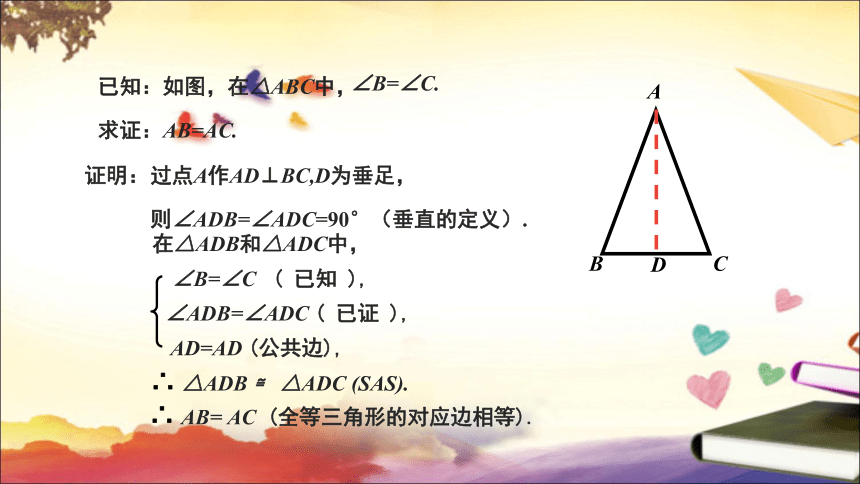
已知:如图,在△ABC中,
求证:AB=AC.
证明:
过点A作AD⊥BC,D为垂足,
则∠ADB=∠ADC=90°(垂直的定义).
∠B=∠C ( 已知 ),
∠ADB=∠ADC ( 已证 ),
AD=AD (公共边),
∴ △ADB ≌ △ADC (SAS).
∴ AB= AC (全等三角形的对应边相等).
在△ADB和△ADC中,
A
B
C
D
∠B=∠C.
一个三角形满足什么条件就是等边三角形
由等腰三角形的判定定理,可得等边三角形的两个判定定理:
1.三个角都相等的三角形是等边三角形;
2.有一个角等于60°的等腰三角形是等边三角形.
探究2:等边三角形的判定
A
B
C
已知:如图,∠A= ∠ B=∠C.
求证: AB=AC=BC.
∵ ∠A= ∠ B,
∴ AC=BC.
∵ ∠ B=∠C,
∴ AB=AC.
∴AB=AC=BC.
证明:
推论1 三个角相等的三角形是等边三角形
推论2:有一个角是60°的等腰三角形是等边三角形.
A
B
C
已知: 若AB=AC , ∠A= 60°.
求证: AB=AC=BC.
证明:∵AB=AC , ∠A= 60 °.
∴∠B=∠C= (180。-∠A)= 60°.
∴∠A= ∠ B=∠C.
∴AB=AC=BC.
证明:∵AB=AC,∠B=60°(已知),
∴∠C=∠B=60°(等边对等角),
∴∠A=60°(三角形内角和定理).
∴∠A=∠B =∠C=60°.
∴△ABC是等边三角形(三个角都相等的三角形是等边三角形).
已知:如图,在△ABC中,AB=AC,∠B=60°.
求证:△ABC是等边三角形.
第二种情况:有一个底角是60°.
A
C
B
60°
【验证】
证明:在△ABC 中,∵∠C =90°,∠A =30°, ∴∠B =60°.
延长BC 到D,使CD =BC,连接AD,则△ACD≌ △ACB (SAS).
∴AD=AB,∠BAC=∠DAC=30°,∠BAD=60°.
则△ABD 是等边三角形. ∴BD=AB.
又∵AC⊥BD,
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°.
求证:BC = AB.
A
B
C
D
∴ BC = AB.
∴BC = BD.
探究3:含30°角的直角三角形的性质
定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
应用格式:
∵在Rt△ABC 中,
∠C =90°,∠A =30°,
A
B
C
∴ BC = AB.
等腰三角形(含等边三角形) 性质 判定的条件
等边对等角
等角对等边
“三线合一”,即等腰三角形顶角平分线,底边上的中线、高线互相重合
有一角是60°的等腰三角形是等边三角形
等边三角形三个内角都相等,且每个角都是60°
三个角都相等的三角形是等边三角形
归纳总结
例1.已知:如图,AB=DC,BD=CA,
求证:△AED是等腰三角形.
A
B
C
D
E
证明:∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS)
∴∠ADB=∠DAC(全等三角形的对应角相等)
∴AE=DE(等角对等边)
∴ △AED是等腰三角形。
例题讲解
例2 如图,在等边三角形ABC中,DE∥BC, 求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
例题讲解
例3 如图,在△ABC中,已知AB=AC=2a,∠B=∠ACB=15°, CD是腰AB上的高,求CD的长.
解:∵∠B=∠ACB=15°,(已知)
∴∠DAC=∠B+∠ACB= 15°+15°=30°,
∵∠ADC=90°,∴CD= AC=a.
(在直角三角形中, 如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半)
例4 如图,上午10 时,一条船从A处出发以每小时10海里的速度向正北航行,从A处测得一礁石C在北偏西30°的方向上.如果这艘船上午8:00从A处出发,10:00到达B处,从B处测得礁石C在北偏西60°方向上.
(1)画出暗礁C的位置;
(2)求从B处到暗礁C的距离.
60°
30°
N
B
A
C
北
解 (1)以B为顶点,向北偏西60作角,这角一边与
AC交于点C,则点C为礁石所在地.
(2)∵∠ACB=60°-30°=30°,(三角形的外角性质)
又∵∠BAC=30°,
∴∠BCA=∠BAC,∴BC=BA.
∵BA=10×(10-8)=20( mile),
∴ BC =20 ( mile).
即从B处到礁石C的距离是20 mile.
1.已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC的周长为______cm.
9
2.在△ABC中,∠B=90°,∠C=30°,AB=3.
则AC=_____ .
A
B
C
3
30°
6
随堂训练
3. 已知:如图,AB=BC ,∠CDE= 120°, DF∥BA,且DF平分∠CDE.
求证:△ABC是等边三角形.
证明:
∵ AB=BC,
∴△ABC是等边三角形.
又∵∠CDE=120°,DF平分∠CDE.
∴ ∠FDC=∠ABC=60°,
∴ △ABC是等腰三角形,
∴ ∠EDF=∠FDC=60°,
又∵DF∥BA,
4.已知:如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D.
求证:BD=
D
A
C
B
30°
证明:∵∠A=30°,CD⊥AB,∠ACB=90°
∴BC= ∠B=60°.
∴∠BCD=30°,
∴BD=
∴BD=
证明:延长BC至D,使CD=BC,连接AD.
∵∠ACB=90°,∴∠ACD=90°.
又∵AC=AC.∴△ACB≌△ACD(SAS).∴AB=AD.
∵CD=BC,∴BC= BD.
又∵BC= AB,∴AB=BD.∴AB=AD=BD,
即△ABD是等边三角形.
∴∠B=60°.在Rt△ABC中,∠BAC=30°.
5.已知:在Rt△ABC中,∠C=90°, BC= AB.
求证:∠BAC=30°.
C
B
A
D
2.等边三角形的判定:
(1)有一个角是60°的等腰三角形是等边三角形.
(2)三个角都相等的三角形是等边三角形.
3.特殊的直角三角形的性质:
(1)在直角三角形中, 如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半.
(2)拓展:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.
4.数学方法:分类的思想.
课堂小结
1.等腰三角形的判定:
(1)有两边相等的三角形是等腰三角形(定义法);
(2)有两个角相等的三角形是等腰三角形(判定定理).
第15章 轴对称图形与等腰三角形
15.3等腰三角形
第3课时 等腰三角形的判定
1.掌握等腰三角形的判定定理,运用定理进行论证和证明;(重点)
2.掌握等边三角形的判定定理.(重点)
3.掌握含30°角的直角三角形的性质并解决有关问题.(难点)
学习目标
等腰三角形有哪些性质?
1.等腰三角形的两底角相等.
(简写成 “等边对等角”)
A
B
C
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
知识回顾
2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.( 简写成“三线合一” )
A
B
C
D
∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(三线合一)
∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(三线合一)
∵AB=AC, AD⊥BC (已知)
∴ BD=CD ,∠BAD=∠CAD (三线合一)
知识讲解
在△ABC中,AB=AC,倘若不留神,它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C,请问,有没有办法把原来的等腰三角形画出来?
A
B
C
A
如图,在△ABC中,如果∠B=∠C,那么AB与AC之间有什么关系吗?
3cm
3cm
测量后发现AB与AC相等
探究1:等腰三角形的判定
定理:有两个角相等的三角形是等
腰三角形.(等角对等边)
等腰三角形的判定定理:
归纳总结
应用格式:
在△ABC中,
∵∠B=∠C, (已知)
∴ AC=AB. (等角对等边)
即△ABC为等腰三角形.
B
C
A
(
(
已知:如图,在△ABC中,
求证:AB=AC.
证明:
过点A作AD⊥BC,D为垂足,
则∠ADB=∠ADC=90°(垂直的定义).
∠B=∠C ( 已知 ),
∠ADB=∠ADC ( 已证 ),
AD=AD (公共边),
∴ △ADB ≌ △ADC (SAS).
∴ AB= AC (全等三角形的对应边相等).
在△ADB和△ADC中,
A
B
C
D
∠B=∠C.
一个三角形满足什么条件就是等边三角形
由等腰三角形的判定定理,可得等边三角形的两个判定定理:
1.三个角都相等的三角形是等边三角形;
2.有一个角等于60°的等腰三角形是等边三角形.
探究2:等边三角形的判定
A
B
C
已知:如图,∠A= ∠ B=∠C.
求证: AB=AC=BC.
∵ ∠A= ∠ B,
∴ AC=BC.
∵ ∠ B=∠C,
∴ AB=AC.
∴AB=AC=BC.
证明:
推论1 三个角相等的三角形是等边三角形
推论2:有一个角是60°的等腰三角形是等边三角形.
A
B
C
已知: 若AB=AC , ∠A= 60°.
求证: AB=AC=BC.
证明:∵AB=AC , ∠A= 60 °.
∴∠B=∠C= (180。-∠A)= 60°.
∴∠A= ∠ B=∠C.
∴AB=AC=BC.
证明:∵AB=AC,∠B=60°(已知),
∴∠C=∠B=60°(等边对等角),
∴∠A=60°(三角形内角和定理).
∴∠A=∠B =∠C=60°.
∴△ABC是等边三角形(三个角都相等的三角形是等边三角形).
已知:如图,在△ABC中,AB=AC,∠B=60°.
求证:△ABC是等边三角形.
第二种情况:有一个底角是60°.
A
C
B
60°
【验证】
证明:在△ABC 中,∵∠C =90°,∠A =30°, ∴∠B =60°.
延长BC 到D,使CD =BC,连接AD,则△ACD≌ △ACB (SAS).
∴AD=AB,∠BAC=∠DAC=30°,∠BAD=60°.
则△ABD 是等边三角形. ∴BD=AB.
又∵AC⊥BD,
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°.
求证:BC = AB.
A
B
C
D
∴ BC = AB.
∴BC = BD.
探究3:含30°角的直角三角形的性质
定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
应用格式:
∵在Rt△ABC 中,
∠C =90°,∠A =30°,
A
B
C
∴ BC = AB.
等腰三角形(含等边三角形) 性质 判定的条件
等边对等角
等角对等边
“三线合一”,即等腰三角形顶角平分线,底边上的中线、高线互相重合
有一角是60°的等腰三角形是等边三角形
等边三角形三个内角都相等,且每个角都是60°
三个角都相等的三角形是等边三角形
归纳总结
例1.已知:如图,AB=DC,BD=CA,
求证:△AED是等腰三角形.
A
B
C
D
E
证明:∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS)
∴∠ADB=∠DAC(全等三角形的对应角相等)
∴AE=DE(等角对等边)
∴ △AED是等腰三角形。
例题讲解
例2 如图,在等边三角形ABC中,DE∥BC, 求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
例题讲解
例3 如图,在△ABC中,已知AB=AC=2a,∠B=∠ACB=15°, CD是腰AB上的高,求CD的长.
解:∵∠B=∠ACB=15°,(已知)
∴∠DAC=∠B+∠ACB= 15°+15°=30°,
∵∠ADC=90°,∴CD= AC=a.
(在直角三角形中, 如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半)
例4 如图,上午10 时,一条船从A处出发以每小时10海里的速度向正北航行,从A处测得一礁石C在北偏西30°的方向上.如果这艘船上午8:00从A处出发,10:00到达B处,从B处测得礁石C在北偏西60°方向上.
(1)画出暗礁C的位置;
(2)求从B处到暗礁C的距离.
60°
30°
N
B
A
C
北
解 (1)以B为顶点,向北偏西60作角,这角一边与
AC交于点C,则点C为礁石所在地.
(2)∵∠ACB=60°-30°=30°,(三角形的外角性质)
又∵∠BAC=30°,
∴∠BCA=∠BAC,∴BC=BA.
∵BA=10×(10-8)=20( mile),
∴ BC =20 ( mile).
即从B处到礁石C的距离是20 mile.
1.已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC的周长为______cm.
9
2.在△ABC中,∠B=90°,∠C=30°,AB=3.
则AC=_____ .
A
B
C
3
30°
6
随堂训练
3. 已知:如图,AB=BC ,∠CDE= 120°, DF∥BA,且DF平分∠CDE.
求证:△ABC是等边三角形.
证明:
∵ AB=BC,
∴△ABC是等边三角形.
又∵∠CDE=120°,DF平分∠CDE.
∴ ∠FDC=∠ABC=60°,
∴ △ABC是等腰三角形,
∴ ∠EDF=∠FDC=60°,
又∵DF∥BA,
4.已知:如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D.
求证:BD=
D
A
C
B
30°
证明:∵∠A=30°,CD⊥AB,∠ACB=90°
∴BC= ∠B=60°.
∴∠BCD=30°,
∴BD=
∴BD=
证明:延长BC至D,使CD=BC,连接AD.
∵∠ACB=90°,∴∠ACD=90°.
又∵AC=AC.∴△ACB≌△ACD(SAS).∴AB=AD.
∵CD=BC,∴BC= BD.
又∵BC= AB,∴AB=BD.∴AB=AD=BD,
即△ABD是等边三角形.
∴∠B=60°.在Rt△ABC中,∠BAC=30°.
5.已知:在Rt△ABC中,∠C=90°, BC= AB.
求证:∠BAC=30°.
C
B
A
D
2.等边三角形的判定:
(1)有一个角是60°的等腰三角形是等边三角形.
(2)三个角都相等的三角形是等边三角形.
3.特殊的直角三角形的性质:
(1)在直角三角形中, 如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半.
(2)拓展:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.
4.数学方法:分类的思想.
课堂小结
1.等腰三角形的判定:
(1)有两边相等的三角形是等腰三角形(定义法);
(2)有两个角相等的三角形是等腰三角形(判定定理).
