苏科版七年级上册2.4.3利用绝对值的性质比较有理数的大小课件(共21张PPT)
文档属性
| 名称 | 苏科版七年级上册2.4.3利用绝对值的性质比较有理数的大小课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
2.4 绝对值与相反数
苏科版初中数学七年级上第2章有理数
第三课时 有理数的大小比较
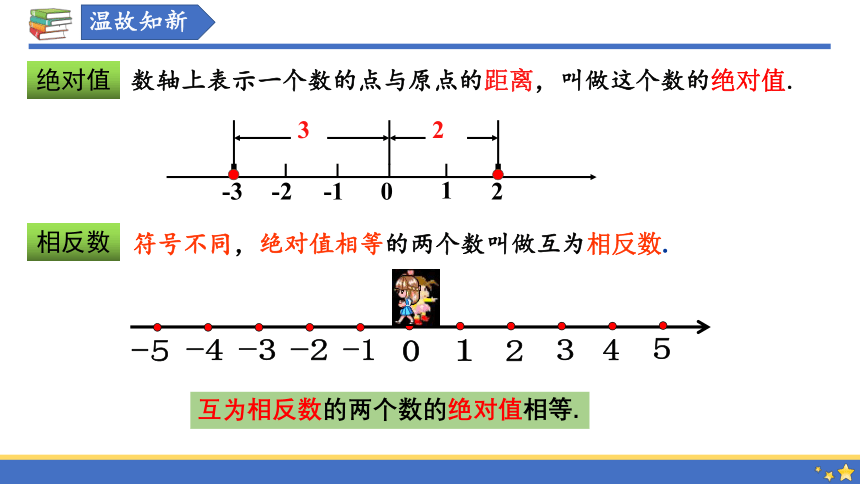
数轴上表示一个数的点与原点的距离,叫做这个数的绝对值.
-3
-2
-1
0
1
2
3
2
符号不同,绝对值相等的两个数叫做互为相反数.
-1
0
-2
1
2
3
4
5
-3
-4
-5
互为相反数的两个数的绝对值相等.
绝对值
相反数
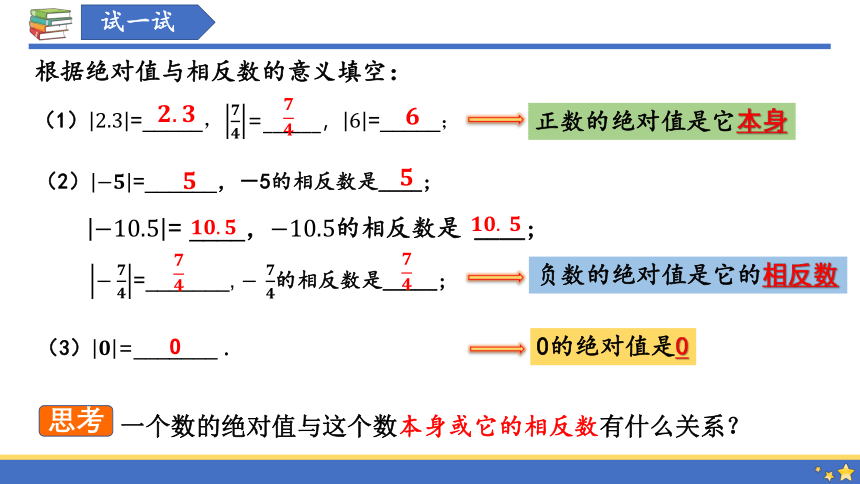
(1)=_____,=______,=_____;
= ____,的相反数是 ____;
(2)=______,-5的相反数是____;
=_______, 的相反数是_____;
(3)=_______ .
0
一个数的绝对值与这个数本身或它的相反数有什么关系?
根据绝对值与相反数的意义填空:
正数的绝对值是它本身
思考
负数的绝对值是它的相反数
0的绝对值是0
正数的绝对值是它本身
绝对值的代数意义:
负数的绝对值是它的相反数
0的绝对值是0
归纳
思考
1.绝对值等于它本身的数有哪些?
2.绝对值等于它的相反数的数有哪些?
正数和0(非负数)
负数和0(非正数)
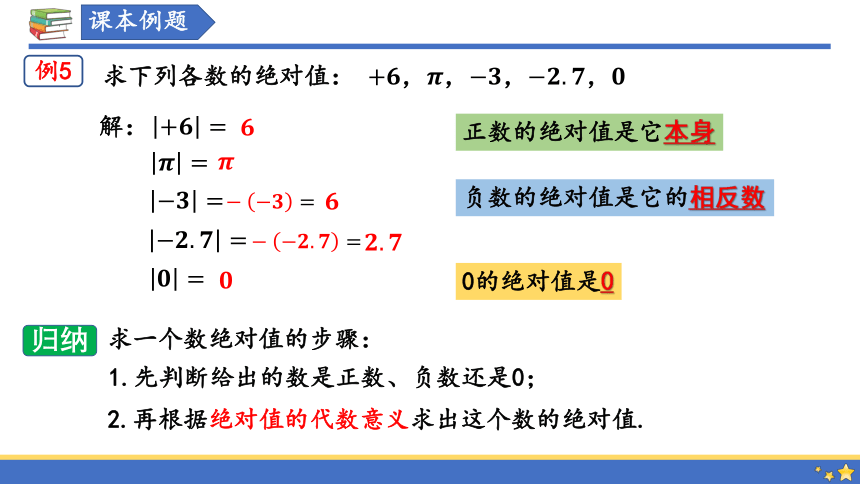
求下列各数的绝对值: ,,,,
解:
1.先判断给出的数是正数、负数还是0;
2.再根据绝对值的代数意义求出这个数的绝对值.
求一个数绝对值的步骤:
例5
正数的绝对值是它本身
负数的绝对值是它的相反数
0的绝对值是0
归纳
如果用字母表示一个数,你知道的绝对值等于什么吗?
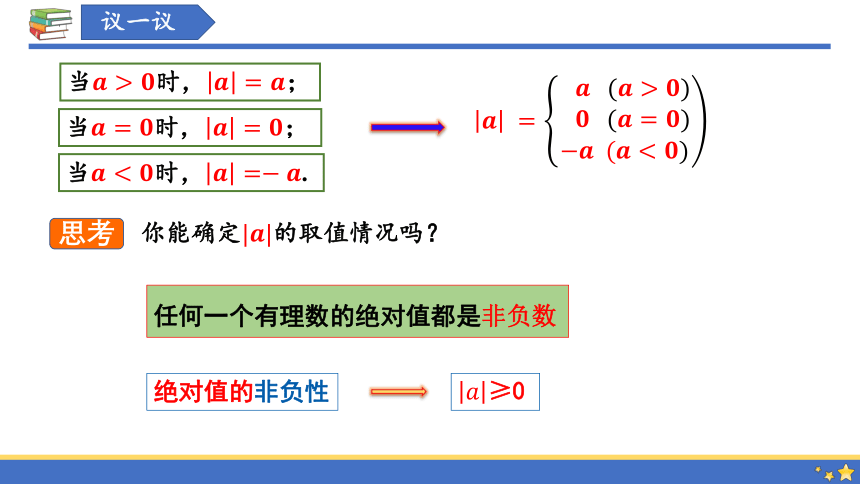
1. 当是正数时, 的绝对值是它本身,
思考
①首先要分清是正数、负数,还是0;
②再根据绝对值的代数意义求出的绝对值.
方法
即当时,;
2.当是时, 的绝对值是,
即当时,;
3.当是负数时, 的绝对值是它的相反数,
即当时,.
你能确定的取值情况吗?
≥0
任何一个有理数的绝对值都是非负数
绝对值的非负性
思考
当时,;
当时,;
当时,.
(1)的符号是______,绝对值是______;
(2)的符号是______,绝对值是______;
(3)符号是“+”号,绝对值是的数是______;
(4)符号是“-”号,绝对值是的数是______;
(5)符号是“+”号,绝对值是的数是______.
填空:
-
+
互为相反数的两个数的绝对值相等,那么绝对值相等的两个数一定互为相反数吗?
绝对值相等的两个数相等或互为相反数.
思考
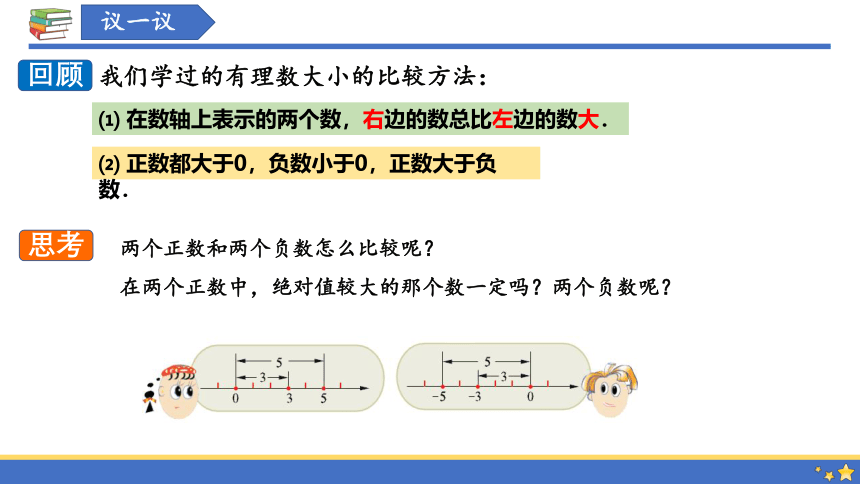
我们学过的有理数大小的比较方法:
⑴ 在数轴上表示的两个数,右边的数总比左边的数大.
⑵ 正数都大于0,负数小于0,正数大于负数.
回顾
思考
两个正数和两个负数怎么比较呢?
在两个正数中,绝对值较大的那个数一定吗?两个负数呢?
在数轴上表示3和5的点都在原点的右边,因此表示5的点在表示3的点的右边,所以 5>3 ;
你能归纳出两个正数、两个负数比较大小的新的方法吗?
数轴上表示两个正数的点都在原点的右边,其中表示绝对值较大的正数的点在另一个点的右边;
数轴上表示两个负数的点都在原点的左边,其中表示绝对值较大的负数的点在另一个点的左边.
在数轴上表示-3和-5的点都在原点的左边,因此表示-3的点在表示-5的点的右边,所以 -3>-5 ;
思考
归纳
两个正数,绝对值大的正数大;
两个负数,绝对值大的负数小.
有理数大小的比较方法:
⑴ 在数轴上表示的两个数,右边的数总比左边的数大.
⑵ 正数都大于0,负数小于0,正数大于负数.
两个正数,绝对值大的正数大;
两个负数,绝对值大的负数小.
比较与的大小.
解:因为,,
且 ,
所以.
先判正负,再用法则.
例5
归纳
两个负数,绝对值大的负数小.
比较与的大小.
解:因为, ,
且 ,
所以
变式
先化简,后判断.
归纳
④
用“<”或“>”填空:
<
<
>
>
①
②
③
⑥
⑤_____
<
<
(2)一个数的绝对值是它的相反数,这个数是 ( )
A、负数 B、0 C、非负数 D、非正数
(1)一个数的绝对值是它本身,这个数是( )
A、正数 B、0 C、非负数 D、非正数
1.选择题:
C
D
(3)下列各式中无论为何值,一定是正数的是( )
A. B. C. +1 D.-(-m)
C
(1)一个数的绝对值是4 ,则这数是4.
(2)有理数的绝对值一定是正数.
(3)若,则.
(4)若,则必为负数.
2.判断题:
3.填空题:
(3)若,则
若,则
(2)若,则的取值范围是 .
(1)若,那么;如果,那么.
或
或
4.(1)绝对值是5的数有几个?是什么数?
(2)绝对值是0的数有几个?是什么数?
(3)有没有绝对值是-1的数?为什么?
(1)绝对值是5的数有个,
分别是和.
(3)没有绝对值是-1的数,
因为任何一个有理数的绝对值都是非负数.
(2)绝对值是0的数有个,
是.
5. 比较和的大小
解析∶
因为这两个负数在数轴上表示比较困难,所以可先分别求出它们的绝对值并比较绝对值的大小,然后根据"两个负数,绝对值大的负数小"得出结论.
解∶
因为||= =
||= =
且
即
所以
绝对值的性质
文字描述
用式子表示
正数的绝对值是它本身
负数的绝对值是它的相反数
0的绝对值是0
≥0
绝对值的非负性
两个正数,绝对值大的正数大;
两个负数,绝对值大的负数小.
比较有理数的大小:
谢 谢!
2.4 绝对值与相反数
苏科版初中数学七年级上第2章有理数
第三课时 有理数的大小比较
数轴上表示一个数的点与原点的距离,叫做这个数的绝对值.
-3
-2
-1
0
1
2
3
2
符号不同,绝对值相等的两个数叫做互为相反数.
-1
0
-2
1
2
3
4
5
-3
-4
-5
互为相反数的两个数的绝对值相等.
绝对值
相反数
(1)=_____,=______,=_____;
= ____,的相反数是 ____;
(2)=______,-5的相反数是____;
=_______, 的相反数是_____;
(3)=_______ .
0
一个数的绝对值与这个数本身或它的相反数有什么关系?
根据绝对值与相反数的意义填空:
正数的绝对值是它本身
思考
负数的绝对值是它的相反数
0的绝对值是0
正数的绝对值是它本身
绝对值的代数意义:
负数的绝对值是它的相反数
0的绝对值是0
归纳
思考
1.绝对值等于它本身的数有哪些?
2.绝对值等于它的相反数的数有哪些?
正数和0(非负数)
负数和0(非正数)
求下列各数的绝对值: ,,,,
解:
1.先判断给出的数是正数、负数还是0;
2.再根据绝对值的代数意义求出这个数的绝对值.
求一个数绝对值的步骤:
例5
正数的绝对值是它本身
负数的绝对值是它的相反数
0的绝对值是0
归纳
如果用字母表示一个数,你知道的绝对值等于什么吗?
1. 当是正数时, 的绝对值是它本身,
思考
①首先要分清是正数、负数,还是0;
②再根据绝对值的代数意义求出的绝对值.
方法
即当时,;
2.当是时, 的绝对值是,
即当时,;
3.当是负数时, 的绝对值是它的相反数,
即当时,.
你能确定的取值情况吗?
≥0
任何一个有理数的绝对值都是非负数
绝对值的非负性
思考
当时,;
当时,;
当时,.
(1)的符号是______,绝对值是______;
(2)的符号是______,绝对值是______;
(3)符号是“+”号,绝对值是的数是______;
(4)符号是“-”号,绝对值是的数是______;
(5)符号是“+”号,绝对值是的数是______.
填空:
-
+
互为相反数的两个数的绝对值相等,那么绝对值相等的两个数一定互为相反数吗?
绝对值相等的两个数相等或互为相反数.
思考
我们学过的有理数大小的比较方法:
⑴ 在数轴上表示的两个数,右边的数总比左边的数大.
⑵ 正数都大于0,负数小于0,正数大于负数.
回顾
思考
两个正数和两个负数怎么比较呢?
在两个正数中,绝对值较大的那个数一定吗?两个负数呢?
在数轴上表示3和5的点都在原点的右边,因此表示5的点在表示3的点的右边,所以 5>3 ;
你能归纳出两个正数、两个负数比较大小的新的方法吗?
数轴上表示两个正数的点都在原点的右边,其中表示绝对值较大的正数的点在另一个点的右边;
数轴上表示两个负数的点都在原点的左边,其中表示绝对值较大的负数的点在另一个点的左边.
在数轴上表示-3和-5的点都在原点的左边,因此表示-3的点在表示-5的点的右边,所以 -3>-5 ;
思考
归纳
两个正数,绝对值大的正数大;
两个负数,绝对值大的负数小.
有理数大小的比较方法:
⑴ 在数轴上表示的两个数,右边的数总比左边的数大.
⑵ 正数都大于0,负数小于0,正数大于负数.
两个正数,绝对值大的正数大;
两个负数,绝对值大的负数小.
比较与的大小.
解:因为,,
且 ,
所以.
先判正负,再用法则.
例5
归纳
两个负数,绝对值大的负数小.
比较与的大小.
解:因为, ,
且 ,
所以
变式
先化简,后判断.
归纳
④
用“<”或“>”填空:
<
<
>
>
①
②
③
⑥
⑤_____
<
<
(2)一个数的绝对值是它的相反数,这个数是 ( )
A、负数 B、0 C、非负数 D、非正数
(1)一个数的绝对值是它本身,这个数是( )
A、正数 B、0 C、非负数 D、非正数
1.选择题:
C
D
(3)下列各式中无论为何值,一定是正数的是( )
A. B. C. +1 D.-(-m)
C
(1)一个数的绝对值是4 ,则这数是4.
(2)有理数的绝对值一定是正数.
(3)若,则.
(4)若,则必为负数.
2.判断题:
3.填空题:
(3)若,则
若,则
(2)若,则的取值范围是 .
(1)若,那么;如果,那么.
或
或
4.(1)绝对值是5的数有几个?是什么数?
(2)绝对值是0的数有几个?是什么数?
(3)有没有绝对值是-1的数?为什么?
(1)绝对值是5的数有个,
分别是和.
(3)没有绝对值是-1的数,
因为任何一个有理数的绝对值都是非负数.
(2)绝对值是0的数有个,
是.
5. 比较和的大小
解析∶
因为这两个负数在数轴上表示比较困难,所以可先分别求出它们的绝对值并比较绝对值的大小,然后根据"两个负数,绝对值大的负数小"得出结论.
解∶
因为||= =
||= =
且
即
所以
绝对值的性质
文字描述
用式子表示
正数的绝对值是它本身
负数的绝对值是它的相反数
0的绝对值是0
≥0
绝对值的非负性
两个正数,绝对值大的正数大;
两个负数,绝对值大的负数小.
比较有理数的大小:
谢 谢!
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
