华师大版七年级上册2.1.1 正数和负数 课件 (共27张PPT)
文档属性
| 名称 | 华师大版七年级上册2.1.1 正数和负数 课件 (共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 08:06:31 | ||
图片预览







文档简介
(共27张PPT)
第2章 有理数
2.1.1 正数和负数
【教学目标】
1、理解正数、负数及0的意义,掌握正数、负数的表示方法.
2、会用正数、负数表示具有相反意义的量. (重点、难点)
数的产生和发展离不开生活和生产的需要,哪位同学知道这些图片介绍的是什么内容?
【引入新知】
数是为了满足生产和生活的需要而产生、发展起来的。
在日常生活中经常会遇到这样的一些量:
1、汽车向东行驶3千米和向西行驶2千米.
2、温度是零上10℃ 和零下5 ℃.
3、收入500元和支出237元.
4、水位升高1.2米和下降0.7米.
5、买进100辆自行车和卖出20辆自行车.
具有相反意义的量
(1)意义相反
(2)含数量的同一种量
相反意义的量:
相反意义的量
与一个量具有相反意义的量不止一个,例:与盈利300元具有相反意义的量有很多,如亏损100元,亏损500元等。
(1)意义相反
(2)含数量的同一种量
(不要求数量相等)
请同学们举几个具有相反意义的量
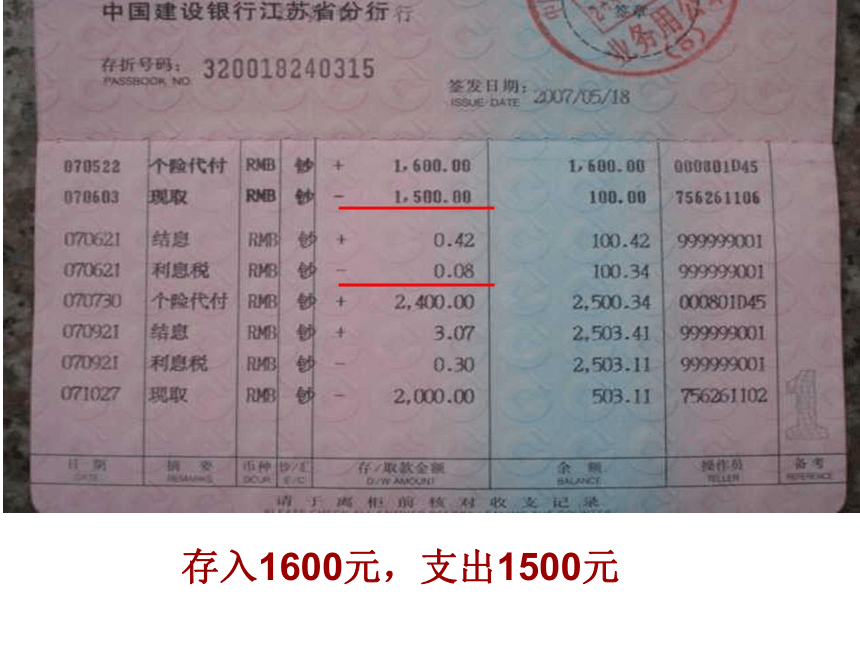
存入1600元,支出1500元
1
9
1
10
1
7
1
8
1
5
1
6
1
3
1
4
1
1
1
2
1
-1
1
-2
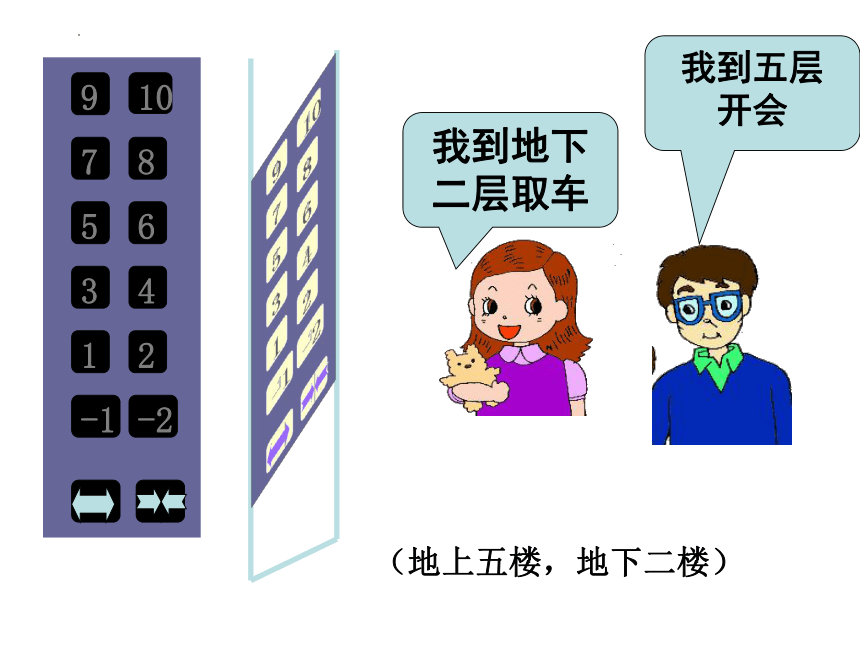
我到五层 开会
我到地下二层取车
(地上五楼,地下二楼)
一般地,对于具有相反意义的量,我们可把其中一种意义的量规定为正的,用过去学过的数(零除外)表示;
这样的数是正数,如:13、3.5、+7......
把与它意义相反的量规定为负的,用过去学过的数(零除外)前面放上一个“ ”(读作“负”)号来表示。
这样的数是负数,如:-2、-2.5、-237......
正数、负数的概念
1、汽车向东行驶3千米和向西行驶2千米.
2、温度是零上10℃ 和零下5 ℃.
3、收入500元和支出237元.
4、水位升高1.2米和下降0.7米.
5、买进100辆自行车和卖出20辆自行车.
你能用正数、负数表示这些量吗
一般情况下,把上升、增加、收入、向北(东)等规定为正,把它们的相反意义规定为负.
正数、负数的概念
例题讲解
填空:
(1)出口货物500吨记作-500,进口货物262吨记作______;
(2)如果产量增加20%,记作______,那么产量减少3%记作______;
(3)向东前进30m记作+30,向西前进10m记作______;
+262
+20%
-3%
-10
例1
生活中的应用
49.5kg ~ 50.5kg
例2
把下列叙述改成使用正数的方法
(1)向南走-20m,即_________;
(2)飞机下降-200米,即_________;
(3)飞机上升-3000米,即_________;
(4)商店赢利-1000元,即_________。
例3
1、(1)向东走5米记+5米,那么向西走6米记作______.
(2)获利200元记作+200元,亏损100元记作_____.
(3)前进10步记作______,后退5步记作______ .
(4)上升10米记作+10,那么-5表示______.
(5)向东记作正,则-12米的意思是______ .
(6) 海面下-200米相当于____________.
课堂练习
2、以海平面为基准,平地高出海平面15米,记作_____,暗礁低于海平面17米,记作_____,山峰高出平地175米,记作_____,海面记作_____。
课堂练习
3、里约奥运会勇夺冠军的中国女排的平均身高为187公分,如果以平均身高为标准,超过部分记为正数,不足部分记为负数,有5名队员分别记为+10,-5,0,+7,-2,则她们的实际身高应是_____________________________.
197、182、187、194、185
课堂练习
4、某机器零件的长度设计为100mm,加工图纸标注的尺寸为(100±0.5)mm,这里的±0.5代表什么意思?合格产品的长度范围是多少?
课堂练习
解释图中的正数和负数的含义
10℃表示白天温度为零上10℃,-5℃表示晚上温度为零下5℃。
它们以什么为基准?
“0”的意义
正数
负数
0
0是分界点
思考
所有正数和0比,有什么关系?
所有负数和0比,有什么关系?
负数 < 0 < 正数
所有正数比0大,所有负数比0小。
零的意义
(1)零既不是正数也不是负数。
(2)零是正数与负数的分界。
(3)零的意义不仅可以表示“没有”,还可以表示特定的意义,如0℃是一个确定的温度。
(4)零常用来表示某些量的基准。
我会做!
比较下列各数的大小
+7与-10 -2.1与0
0 与+ - 与+
答:
+7 >-10
-2.1 < 0
0<+
-
<+
例4
判断下列说法,正确打√,错误打×
1.加正号的数是正数,加负号的数是负数
2.0是最小的正数
3.字母a既可是正数,也可是负数,也可是0
4.任意一个数,不是正数就是负数
例5
5.0既是正数,又是负数
6.0既不是正数,也不是负数
⑴我们在小学学习过的数除零以外都是正数,正数都是大于零的数.
⑵零既不是正数,也不是负数,它是正数与负数的分界点,它前面带上正号是零,带上负号也是零.
⑶通常用正数和负数来表示一对具有相反意义的量.
⑷在小学学过的数中,除零以外,其余的数都是正数(“+”号可以省略不写);在正数的前面加上一个负号(“-”)的数是负数(负号不能省略).
【教学总结】
中国是世界上最早认识和应用负数的国家。早在2000多年前的《九章算术》中,就有正数和负数的记载。在古代,人们为区别正数和负数,常用红筹表示正,黑筹表示负,也有的将算筹正放或斜放加以区别。而西方认识正数、负数则要迟于中国数百年。
“月有阴晴圆缺,人有悲欢离合”,这是宋代词人苏东坡写下的被人们广为传诵的佳句,其中,阴与晴、悲与欢、离与合,都是自然世界、人类生活中截然相反的状态的真实描绘,这些矛盾的东西融为一体,营造出了和谐而真实的氛围。
在数学世界里,一对对具有相反意义的量也是这个大家庭的成员,它们彼此矛盾而又各平相处,为数学世界增添了无穷的魅力。
为什么要引入负数
第2章 有理数
2.1.1 正数和负数
【教学目标】
1、理解正数、负数及0的意义,掌握正数、负数的表示方法.
2、会用正数、负数表示具有相反意义的量. (重点、难点)
数的产生和发展离不开生活和生产的需要,哪位同学知道这些图片介绍的是什么内容?
【引入新知】
数是为了满足生产和生活的需要而产生、发展起来的。
在日常生活中经常会遇到这样的一些量:
1、汽车向东行驶3千米和向西行驶2千米.
2、温度是零上10℃ 和零下5 ℃.
3、收入500元和支出237元.
4、水位升高1.2米和下降0.7米.
5、买进100辆自行车和卖出20辆自行车.
具有相反意义的量
(1)意义相反
(2)含数量的同一种量
相反意义的量:
相反意义的量
与一个量具有相反意义的量不止一个,例:与盈利300元具有相反意义的量有很多,如亏损100元,亏损500元等。
(1)意义相反
(2)含数量的同一种量
(不要求数量相等)
请同学们举几个具有相反意义的量
存入1600元,支出1500元
1
9
1
10
1
7
1
8
1
5
1
6
1
3
1
4
1
1
1
2
1
-1
1
-2
我到五层 开会
我到地下二层取车
(地上五楼,地下二楼)
一般地,对于具有相反意义的量,我们可把其中一种意义的量规定为正的,用过去学过的数(零除外)表示;
这样的数是正数,如:13、3.5、+7......
把与它意义相反的量规定为负的,用过去学过的数(零除外)前面放上一个“ ”(读作“负”)号来表示。
这样的数是负数,如:-2、-2.5、-237......
正数、负数的概念
1、汽车向东行驶3千米和向西行驶2千米.
2、温度是零上10℃ 和零下5 ℃.
3、收入500元和支出237元.
4、水位升高1.2米和下降0.7米.
5、买进100辆自行车和卖出20辆自行车.
你能用正数、负数表示这些量吗
一般情况下,把上升、增加、收入、向北(东)等规定为正,把它们的相反意义规定为负.
正数、负数的概念
例题讲解
填空:
(1)出口货物500吨记作-500,进口货物262吨记作______;
(2)如果产量增加20%,记作______,那么产量减少3%记作______;
(3)向东前进30m记作+30,向西前进10m记作______;
+262
+20%
-3%
-10
例1
生活中的应用
49.5kg ~ 50.5kg
例2
把下列叙述改成使用正数的方法
(1)向南走-20m,即_________;
(2)飞机下降-200米,即_________;
(3)飞机上升-3000米,即_________;
(4)商店赢利-1000元,即_________。
例3
1、(1)向东走5米记+5米,那么向西走6米记作______.
(2)获利200元记作+200元,亏损100元记作_____.
(3)前进10步记作______,后退5步记作______ .
(4)上升10米记作+10,那么-5表示______.
(5)向东记作正,则-12米的意思是______ .
(6) 海面下-200米相当于____________.
课堂练习
2、以海平面为基准,平地高出海平面15米,记作_____,暗礁低于海平面17米,记作_____,山峰高出平地175米,记作_____,海面记作_____。
课堂练习
3、里约奥运会勇夺冠军的中国女排的平均身高为187公分,如果以平均身高为标准,超过部分记为正数,不足部分记为负数,有5名队员分别记为+10,-5,0,+7,-2,则她们的实际身高应是_____________________________.
197、182、187、194、185
课堂练习
4、某机器零件的长度设计为100mm,加工图纸标注的尺寸为(100±0.5)mm,这里的±0.5代表什么意思?合格产品的长度范围是多少?
课堂练习
解释图中的正数和负数的含义
10℃表示白天温度为零上10℃,-5℃表示晚上温度为零下5℃。
它们以什么为基准?
“0”的意义
正数
负数
0
0是分界点
思考
所有正数和0比,有什么关系?
所有负数和0比,有什么关系?
负数 < 0 < 正数
所有正数比0大,所有负数比0小。
零的意义
(1)零既不是正数也不是负数。
(2)零是正数与负数的分界。
(3)零的意义不仅可以表示“没有”,还可以表示特定的意义,如0℃是一个确定的温度。
(4)零常用来表示某些量的基准。
我会做!
比较下列各数的大小
+7与-10 -2.1与0
0 与+ - 与+
答:
+7 >-10
-2.1 < 0
0<+
-
<+
例4
判断下列说法,正确打√,错误打×
1.加正号的数是正数,加负号的数是负数
2.0是最小的正数
3.字母a既可是正数,也可是负数,也可是0
4.任意一个数,不是正数就是负数
例5
5.0既是正数,又是负数
6.0既不是正数,也不是负数
⑴我们在小学学习过的数除零以外都是正数,正数都是大于零的数.
⑵零既不是正数,也不是负数,它是正数与负数的分界点,它前面带上正号是零,带上负号也是零.
⑶通常用正数和负数来表示一对具有相反意义的量.
⑷在小学学过的数中,除零以外,其余的数都是正数(“+”号可以省略不写);在正数的前面加上一个负号(“-”)的数是负数(负号不能省略).
【教学总结】
中国是世界上最早认识和应用负数的国家。早在2000多年前的《九章算术》中,就有正数和负数的记载。在古代,人们为区别正数和负数,常用红筹表示正,黑筹表示负,也有的将算筹正放或斜放加以区别。而西方认识正数、负数则要迟于中国数百年。
“月有阴晴圆缺,人有悲欢离合”,这是宋代词人苏东坡写下的被人们广为传诵的佳句,其中,阴与晴、悲与欢、离与合,都是自然世界、人类生活中截然相反的状态的真实描绘,这些矛盾的东西融为一体,营造出了和谐而真实的氛围。
在数学世界里,一对对具有相反意义的量也是这个大家庭的成员,它们彼此矛盾而又各平相处,为数学世界增添了无穷的魅力。
为什么要引入负数
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
