4.1.2 点、线、面、体 同步练习(含答案)
文档属性
| 名称 | 4.1.2 点、线、面、体 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 00:00:00 | ||
图片预览


文档简介
4.1 几何图形
4.1.2 点、线、面、体
【知识梳理】
1.长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是 .几何体简称 .
2.包围着体的是 ,面与面相交成 ,线与线相交成 .
3.点动成 ,线动成 ,面动成 .
【基础强化】
知识点1 构成图形的元素
1.下列几何体的所有面都不是平面图形的是( )
A.正方体 B.圆锥 C.圆柱 D.球
2.下列几何体中没有曲面的是( )
A.球 B.圆柱 C.棱柱 D.圆锥
3.在球、圆锥、圆柱、棱柱中,由曲面和平面围成的是( )
A.球和圆锥 B.球和圆柱 C.圆锥和圆柱 D.圆柱和棱柱
4.若一个棱柱有12个顶点,则下列说法正确的是( )
A.这个棱柱有5个侧面 B.这个棱柱有5个侧棱
C.这个棱柱的底面是六边形 D.这个棱柱是一个十二棱柱
5.如图所示的立体图形是由 个面组成的,面与面相交成 条线.
6.观察如图所示的棱锥,回答下列问题:
(1)这个图形是平面图形还是立体图形
(2)图中有多少个顶点 多少条线段 多少个平面
知识点2 点、线、面、体的转化
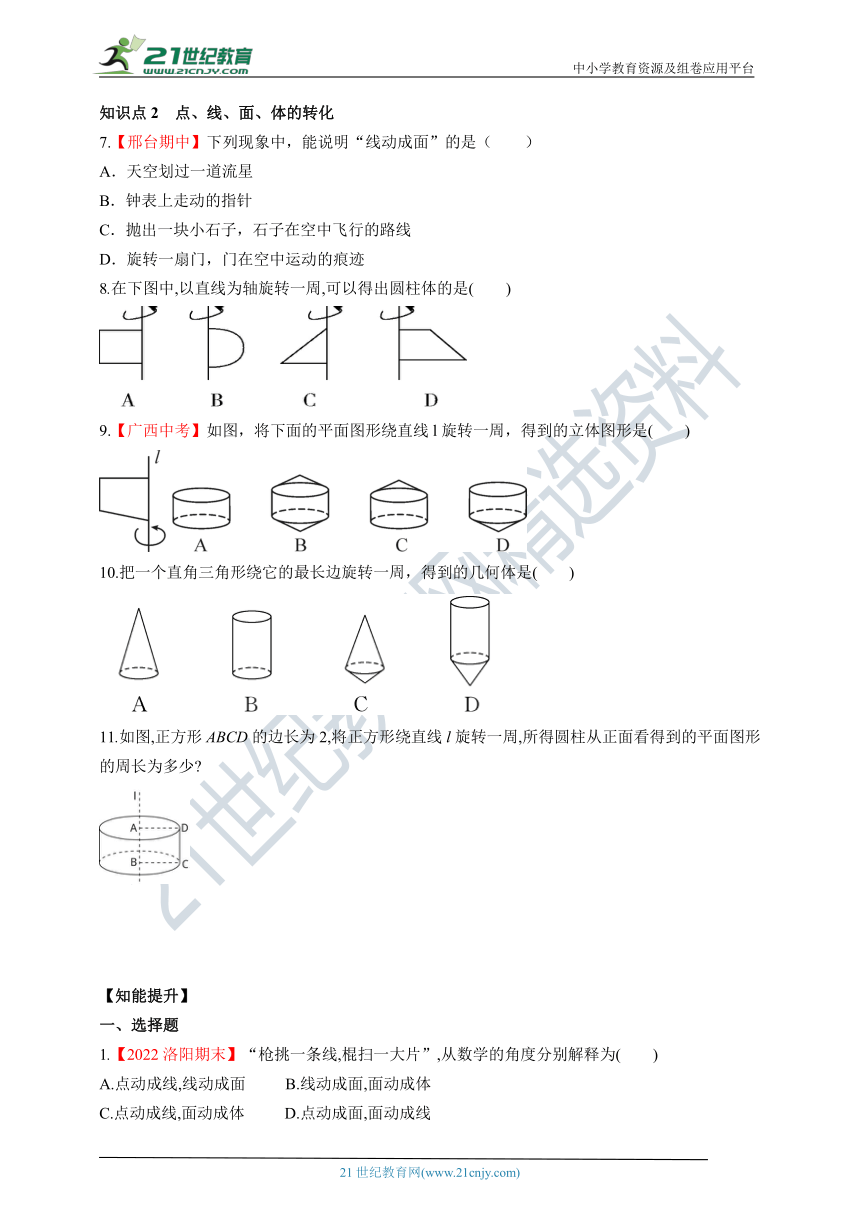
7.【邢台期中】下列现象中,能说明“线动成面”的是( )
A.天空划过一道流星
B.钟表上走动的指针
C.抛出一块小石子,石子在空中飞行的路线
D.旋转一扇门,门在空中运动的痕迹
8.在下图中,以直线为轴旋转一周,可以得出圆柱体的是( )
9.【广西中考】如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是( )
10.把一个直角三角形绕它的最长边旋转一周,得到的几何体是( )
11.如图,正方形ABCD的边长为2,将正方形绕直线l旋转一周,所得圆柱从正面看得到的平面图形的周长为多少
【知能提升】
一、选择题
1.【2022洛阳期末】“枪挑一条线,棍扫一大片”,从数学的角度分别解释为( )
A.点动成线,线动成面 B.线动成面,面动成体
C.点动成线,面动成体 D.点动成面,面动成线
2.下列说法:①圆柱由3个面围成,这3个面都是平的;②圆锥由2个面围成,这2个面中,1个是平的,1个是曲的;③球仅由1个面围成,这个面是平的;④正方体由6个面围成,这6个面都是平的.其中正确的为( )
A.①② B.②③ C.②④ D.③④
3.若一个棱柱有12个顶点,则下列说法中正确的是 ( )
A.这个棱柱有5个侧面 B.这个棱柱有5条侧棱
C.这个棱柱的底面是六边形 D.这个棱柱是一个十二棱柱
4.有下列说法:①一点在平面内运动的过程中,能形成一条线段;②一条线段在平面内运动的过程中,能形成一个平行四边形;③一个三角形在空间内运动的过程中,能形成一个三棱柱;④一个圆形在空间内平移的过程中,能形成一个球体.其中正确的是( )
A.①②③④ B.①②③ C.②③④ D.①③④
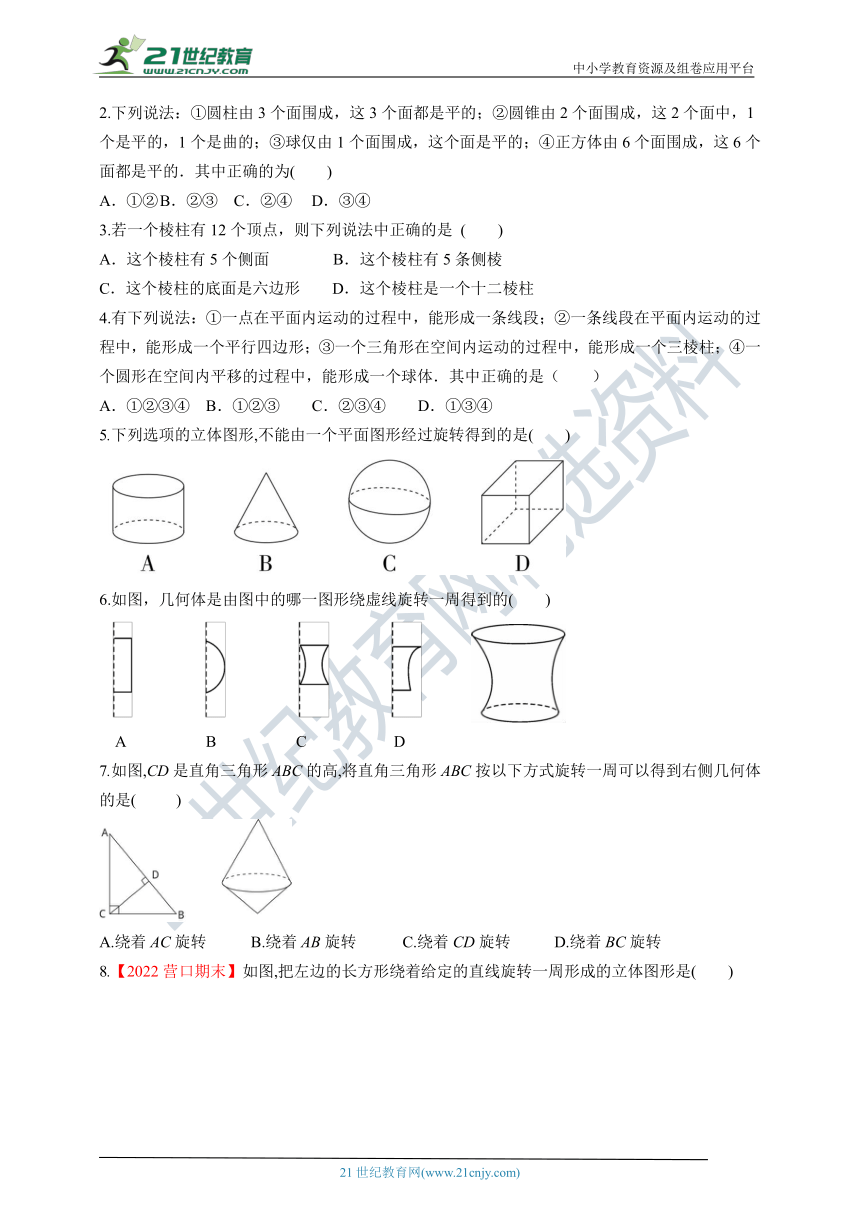
5.下列选项的立体图形,不能由一个平面图形经过旋转得到的是( )
6.如图,几何体是由图中的哪一图形绕虚线旋转一周得到的( )
A B C D
7.如图,CD是直角三角形ABC的高,将直角三角形ABC按以下方式旋转一周可以得到右侧几何体的是( )
A.绕着AC旋转 B.绕着AB旋转 C.绕着CD旋转 D.绕着BC旋转
8.【2022营口期末】如图,把左边的长方形绕着给定的直线旋转一周形成的立体图形是( )
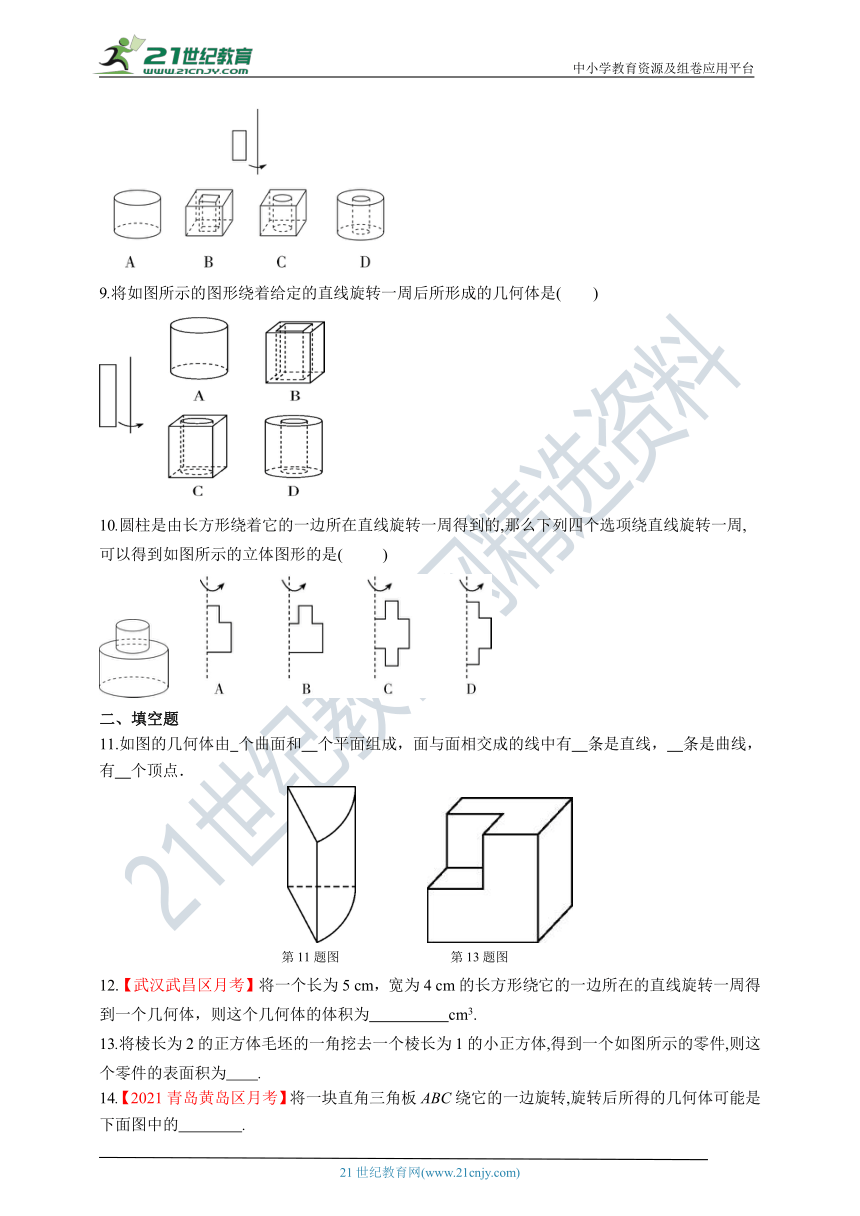
9.将如图所示的图形绕着给定的直线旋转一周后所形成的几何体是( )
10.圆柱是由长方形绕着它的一边所在直线旋转一周得到的,那么下列四个选项绕直线旋转一周,可以得到如图所示的立体图形的是( )
二、填空题
11.如图的几何体由 个曲面和 个平面组成,面与面相交成的线中有 条是直线, 条是曲线,有 个顶点.
第11题图 第13题图
12.【武汉武昌区月考】将一个长为5 cm,宽为4 cm的长方形绕它的一边所在的直线旋转一周得到一个几何体,则这个几何体的体积为 cm3.
13.将棱长为2的正方体毛坯的一角挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
14.【2021青岛黄岛区月考】将一块直角三角板ABC绕它的一边旋转,旋转后所得的几何体可能是下面图中的 .
三、解答题
15.如图,将一个长方形在直线m上翻滚,请用圆规在图中作出点A所经过的路径.
16.如图是一个长为4 cm、宽为3 cm的长方形纸片,该长方形纸片分别绕长、宽所在直线旋转一周(如图1,图2).请你通过计算,说明哪种方式得到的几何体的体积较大.(结果保留π)
17.求图中阴影部分的面积.(单位:cm)
18.如图所示,左边是小颖的圆柱形的笔筒,右边是小彬的六棱柱形的笔筒.仔细观察两个笔筒,并回答下面问题.
(1)圆柱、六棱柱各由几个面组成 它们都是平的吗
(2)圆柱形笔筒的侧面与下底面相交成几条线 它(们)是直的吗
(3)六棱柱有几个顶点 经过每个顶点有几条棱
(4)试写出圆柱与棱柱的相同点与不同点.
19.新年晚会是我们最欢乐的时候.会场上悬挂着五彩缤纷的小装饰,其中有各种各样的立体图形.
(1)数一下每一个多面体具有的顶点数(V)、棱数(E)和面数(F),并且把结果记入表中:
多面体 顶点数(V) 面数(F) 棱数(E)
正四面体 4 4 6
正方体
正八面体
正十二面体
正二十面体 12 20 30
(2)观察表中的数据,猜想多面体的顶点数(V)、面数(F)和棱数(E)之间的关系.
(3)18世纪瑞士数学家欧拉证明了这一令人惊叹的关系式,即欧拉公式.若已知一个多面体的顶点数V=196,棱的条数E=294,请你用欧拉公式求出这个多面体的面数.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【知识梳理】
1.长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体.几何体简称体.
2.包围着体的是面 ,面与面相交成线 ,线与线相交成点 .
3.点动成线 ,线动成面 ,面动成体 .
【基础强化】
知识点1 构成图形的元素
1.下列几何体的所有面都不是平面图形的是( D )
A.正方体 B.圆锥 C.圆柱 D.球
2.下列几何体中没有曲面的是( C )
A.球 B.圆柱 C.棱柱 D.圆锥
3.在球、圆锥、圆柱、棱柱中,由曲面和平面围成的是( C )
A.球和圆锥 B.球和圆柱 C.圆锥和圆柱 D.圆柱和棱柱
4.若一个棱柱有12个顶点,则下列说法正确的是( C )
A.这个棱柱有5个侧面 B.这个棱柱有5个侧棱
C.这个棱柱的底面是六边形 D.这个棱柱是一个十二棱柱
5.如图所示的立体图形是由 4 个面组成的,面与面相交成 6 条线.
6.观察如图所示的棱锥,回答下列问题:
(1)这个图形是平面图形还是立体图形
(2)图中有多少个顶点 多少条线段 多少个平面
解:(1)立体图形.
(2)图中有5个顶点,8条线段,5个平面.
知识点2 点、线、面、体的转化
7.【邢台期中】下列现象中,能说明“线动成面”的是( B )
A.天空划过一道流星
B.钟表上走动的指针
C.抛出一块小石子,石子在空中飞行的路线
D.旋转一扇门,门在空中运动的痕迹
8.在下图中,以直线为轴旋转一周,可以得出圆柱体的是( A )
9.【广西中考】如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是( D )
10.把一个直角三角形绕它的最长边旋转一周,得到的几何体是( C )
11.如图,正方形ABCD的边长为2,将正方形绕直线l旋转一周,所得圆柱从正面看得到的平面图形的周长为多少
解:因为该圆柱从正面看是一个长为4、宽为2的长方形,所以它的周长为12.
【知能提升】
一、选择题
1.【2022洛阳期末】“枪挑一条线,棍扫一大片”,从数学的角度分别解释为( A )
A.点动成线,线动成面 B.线动成面,面动成体
C.点动成线,面动成体 D.点动成面,面动成线
2.下列说法:①圆柱由3个面围成,这3个面都是平的;②圆锥由2个面围成,这2个面中,1个是平的,1个是曲的;③球仅由1个面围成,这个面是平的;④正方体由6个面围成,这6个面都是平的.其中正确的为( C )
A.①② B.②③ C.②④ D.③④
3.若一个棱柱有12个顶点,则下列说法中正确的是 ( C )
A.这个棱柱有5个侧面 B.这个棱柱有5条侧棱
C.这个棱柱的底面是六边形 D.这个棱柱是一个十二棱柱
4.有下列说法:①一点在平面内运动的过程中,能形成一条线段;②一条线段在平面内运动的过程中,能形成一个平行四边形;③一个三角形在空间内运动的过程中,能形成一个三棱柱;④一个圆形在空间内平移的过程中,能形成一个球体.其中正确的是( B )
A.①②③④ B.①②③ C.②③④ D.①③④
5.下列选项的立体图形,不能由一个平面图形经过旋转得到的是( D )
【解析】A项,可由长方形经过旋转得到;B项,可由直角三角形经过旋转得到;C项,可由半圆经过旋转得到;D项,不能由一个平面图形经过旋转得到.
6.如图,几何体是由图中的哪一图形绕虚线旋转一周得到的( D )
A B C D
7.如图,CD是直角三角形ABC的高,将直角三角形ABC按以下方式旋转一周可以得到右侧几何体的是( B )
A.绕着AC旋转 B.绕着AB旋转 C.绕着CD旋转 D.绕着BC旋转
8.【2022营口期末】如图,把左边的长方形绕着给定的直线旋转一周形成的立体图形是( D )
9.将如图所示的图形绕着给定的直线旋转一周后所形成的几何体是( D )
10.圆柱是由长方形绕着它的一边所在直线旋转一周得到的,那么下列四个选项绕直线旋转一周,可以得到如图所示的立体图形的是( A )
二、填空题
11.如图的几何体由 1个曲面和 4 个平面组成,面与面相交成的线中有 7 条是直线, 2 条是曲线,有 6 个顶点.
第11题图 第13题图
12.【武汉武昌区月考】将一个长为5 cm,宽为4 cm的长方形绕它的一边所在的直线旋转一周得到一个几何体,则这个几何体的体积为80π或100π cm3.
13.将棱长为2的正方体毛坯的一角挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 24 .
14.【2021青岛黄岛区月考】将一块直角三角板ABC绕它的一边旋转,旋转后所得的几何体可能是下面图中的 .
【答案】(2)(3)(4)
【解析】以AC边所在的直线为轴,旋转一周形成题图(2)的圆锥体;以BC边所在的直线为轴,旋转一周形成题图(3)的圆锥体;以AB边所在的直线为轴,旋转一周形成题图(4)的立体图形.
三、解答题
15.如图,将一个长方形在直线m上翻滚,请用圆规在图中作出点A所经过的路径.
【解析】由题意可知,A点所经过的路径是先以长方形的长为半径,旋转90°,再以长方形的对角线为半径,旋转90°所对应的弧长.
【答案】
16.如图是一个长为4 cm、宽为3 cm的长方形纸片,该长方形纸片分别绕长、宽所在直线旋转一周(如图1,图2).请你通过计算,说明哪种方式得到的几何体的体积较大.(结果保留π)
解:绕长边旋转得到的圆柱的底面半径为3 cm、高为4 cm,体积为π×32×4=36π(cm3);
绕短边旋转得到的圆柱的底面半径为4 cm、高为3 cm,体积为π×42×3=48π(cm3).
因此绕短边旋转得到的圆柱的体积较大.
17.求图中阴影部分的面积.(单位:cm)
解:图中两个正方形的面积之和为S1=8×8+5×5=89(cm2),
空白部分的面积之和为S2=×(8+5)×5=64.5(cm2),
所以阴影部分的面积为S=S1-S2=89-64.5=24.5(cm2).
18.如图所示,左边是小颖的圆柱形的笔筒,右边是小彬的六棱柱形的笔筒.仔细观察两个笔筒,并回答下面问题.
(1)圆柱、六棱柱各由几个面组成 它们都是平的吗
(2)圆柱形笔筒的侧面与下底面相交成几条线 它(们)是直的吗
(3)六棱柱有几个顶点 经过每个顶点有几条棱
(4)试写出圆柱与棱柱的相同点与不同点.
解:(1)圆柱由3个面组成,六棱柱由8个面组成,圆柱有2个平面,1个曲面,六棱柱的8个面都是平面.
(2)圆柱形笔筒的侧面与下底面相交形成1条线,是曲线.
(3)六棱柱共有12个顶点,经过每个顶点有3条棱.
(4)棱柱与圆柱的相同点:都是柱体.
不同点:棱柱与圆柱的底面形状不同,棱柱的底面是多边形,圆柱的底面是圆形,圆柱的侧面是曲面,而棱柱的侧面是长方形.(答案不唯一,合理即可)
19.新年晚会是我们最欢乐的时候.会场上悬挂着五彩缤纷的小装饰,其中有各种各样的立体图形.
(1)数一下每一个多面体具有的顶点数(V)、棱数(E)和面数(F),并且把结果记入表中:
多面体 顶点数(V) 面数(F) 棱数(E)
正四面体 4 4 6
正方体 8 6 12
正八面体 6 8 12
正十二面体 20 12 30
正二十面体 12 20 30
(2)观察表中的数据,猜想多面体的顶点数(V)、面数(F)和棱数(E)之间的关系.
(3)18世纪瑞士数学家欧拉证明了这一令人惊叹的关系式,即欧拉公式.若已知一个多面体的顶点数V=196,棱的条数E=294,请你用欧拉公式求出这个多面体的面数.
解:(2)因为4+4-6=2,8+6-12=2,6+8-12=2,20+12-30=2,12+20-30=2,所以V+F-E=2.
(3)由V+F-E=2,得196+F-294=2,则F=100,所以这个多面体的面数为100.
4.1.2 点、线、面、体
【知识梳理】
1.长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是 .几何体简称 .
2.包围着体的是 ,面与面相交成 ,线与线相交成 .
3.点动成 ,线动成 ,面动成 .
【基础强化】
知识点1 构成图形的元素
1.下列几何体的所有面都不是平面图形的是( )
A.正方体 B.圆锥 C.圆柱 D.球
2.下列几何体中没有曲面的是( )
A.球 B.圆柱 C.棱柱 D.圆锥
3.在球、圆锥、圆柱、棱柱中,由曲面和平面围成的是( )
A.球和圆锥 B.球和圆柱 C.圆锥和圆柱 D.圆柱和棱柱
4.若一个棱柱有12个顶点,则下列说法正确的是( )
A.这个棱柱有5个侧面 B.这个棱柱有5个侧棱
C.这个棱柱的底面是六边形 D.这个棱柱是一个十二棱柱
5.如图所示的立体图形是由 个面组成的,面与面相交成 条线.
6.观察如图所示的棱锥,回答下列问题:
(1)这个图形是平面图形还是立体图形
(2)图中有多少个顶点 多少条线段 多少个平面
知识点2 点、线、面、体的转化
7.【邢台期中】下列现象中,能说明“线动成面”的是( )
A.天空划过一道流星
B.钟表上走动的指针
C.抛出一块小石子,石子在空中飞行的路线
D.旋转一扇门,门在空中运动的痕迹
8.在下图中,以直线为轴旋转一周,可以得出圆柱体的是( )
9.【广西中考】如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是( )
10.把一个直角三角形绕它的最长边旋转一周,得到的几何体是( )
11.如图,正方形ABCD的边长为2,将正方形绕直线l旋转一周,所得圆柱从正面看得到的平面图形的周长为多少
【知能提升】
一、选择题
1.【2022洛阳期末】“枪挑一条线,棍扫一大片”,从数学的角度分别解释为( )
A.点动成线,线动成面 B.线动成面,面动成体
C.点动成线,面动成体 D.点动成面,面动成线
2.下列说法:①圆柱由3个面围成,这3个面都是平的;②圆锥由2个面围成,这2个面中,1个是平的,1个是曲的;③球仅由1个面围成,这个面是平的;④正方体由6个面围成,这6个面都是平的.其中正确的为( )
A.①② B.②③ C.②④ D.③④
3.若一个棱柱有12个顶点,则下列说法中正确的是 ( )
A.这个棱柱有5个侧面 B.这个棱柱有5条侧棱
C.这个棱柱的底面是六边形 D.这个棱柱是一个十二棱柱
4.有下列说法:①一点在平面内运动的过程中,能形成一条线段;②一条线段在平面内运动的过程中,能形成一个平行四边形;③一个三角形在空间内运动的过程中,能形成一个三棱柱;④一个圆形在空间内平移的过程中,能形成一个球体.其中正确的是( )
A.①②③④ B.①②③ C.②③④ D.①③④
5.下列选项的立体图形,不能由一个平面图形经过旋转得到的是( )
6.如图,几何体是由图中的哪一图形绕虚线旋转一周得到的( )
A B C D
7.如图,CD是直角三角形ABC的高,将直角三角形ABC按以下方式旋转一周可以得到右侧几何体的是( )
A.绕着AC旋转 B.绕着AB旋转 C.绕着CD旋转 D.绕着BC旋转
8.【2022营口期末】如图,把左边的长方形绕着给定的直线旋转一周形成的立体图形是( )
9.将如图所示的图形绕着给定的直线旋转一周后所形成的几何体是( )
10.圆柱是由长方形绕着它的一边所在直线旋转一周得到的,那么下列四个选项绕直线旋转一周,可以得到如图所示的立体图形的是( )
二、填空题
11.如图的几何体由 个曲面和 个平面组成,面与面相交成的线中有 条是直线, 条是曲线,有 个顶点.
第11题图 第13题图
12.【武汉武昌区月考】将一个长为5 cm,宽为4 cm的长方形绕它的一边所在的直线旋转一周得到一个几何体,则这个几何体的体积为 cm3.
13.将棱长为2的正方体毛坯的一角挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
14.【2021青岛黄岛区月考】将一块直角三角板ABC绕它的一边旋转,旋转后所得的几何体可能是下面图中的 .
三、解答题
15.如图,将一个长方形在直线m上翻滚,请用圆规在图中作出点A所经过的路径.
16.如图是一个长为4 cm、宽为3 cm的长方形纸片,该长方形纸片分别绕长、宽所在直线旋转一周(如图1,图2).请你通过计算,说明哪种方式得到的几何体的体积较大.(结果保留π)
17.求图中阴影部分的面积.(单位:cm)
18.如图所示,左边是小颖的圆柱形的笔筒,右边是小彬的六棱柱形的笔筒.仔细观察两个笔筒,并回答下面问题.
(1)圆柱、六棱柱各由几个面组成 它们都是平的吗
(2)圆柱形笔筒的侧面与下底面相交成几条线 它(们)是直的吗
(3)六棱柱有几个顶点 经过每个顶点有几条棱
(4)试写出圆柱与棱柱的相同点与不同点.
19.新年晚会是我们最欢乐的时候.会场上悬挂着五彩缤纷的小装饰,其中有各种各样的立体图形.
(1)数一下每一个多面体具有的顶点数(V)、棱数(E)和面数(F),并且把结果记入表中:
多面体 顶点数(V) 面数(F) 棱数(E)
正四面体 4 4 6
正方体
正八面体
正十二面体
正二十面体 12 20 30
(2)观察表中的数据,猜想多面体的顶点数(V)、面数(F)和棱数(E)之间的关系.
(3)18世纪瑞士数学家欧拉证明了这一令人惊叹的关系式,即欧拉公式.若已知一个多面体的顶点数V=196,棱的条数E=294,请你用欧拉公式求出这个多面体的面数.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【知识梳理】
1.长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体.几何体简称体.
2.包围着体的是面 ,面与面相交成线 ,线与线相交成点 .
3.点动成线 ,线动成面 ,面动成体 .
【基础强化】
知识点1 构成图形的元素
1.下列几何体的所有面都不是平面图形的是( D )
A.正方体 B.圆锥 C.圆柱 D.球
2.下列几何体中没有曲面的是( C )
A.球 B.圆柱 C.棱柱 D.圆锥
3.在球、圆锥、圆柱、棱柱中,由曲面和平面围成的是( C )
A.球和圆锥 B.球和圆柱 C.圆锥和圆柱 D.圆柱和棱柱
4.若一个棱柱有12个顶点,则下列说法正确的是( C )
A.这个棱柱有5个侧面 B.这个棱柱有5个侧棱
C.这个棱柱的底面是六边形 D.这个棱柱是一个十二棱柱
5.如图所示的立体图形是由 4 个面组成的,面与面相交成 6 条线.
6.观察如图所示的棱锥,回答下列问题:
(1)这个图形是平面图形还是立体图形
(2)图中有多少个顶点 多少条线段 多少个平面
解:(1)立体图形.
(2)图中有5个顶点,8条线段,5个平面.
知识点2 点、线、面、体的转化
7.【邢台期中】下列现象中,能说明“线动成面”的是( B )
A.天空划过一道流星
B.钟表上走动的指针
C.抛出一块小石子,石子在空中飞行的路线
D.旋转一扇门,门在空中运动的痕迹
8.在下图中,以直线为轴旋转一周,可以得出圆柱体的是( A )
9.【广西中考】如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是( D )
10.把一个直角三角形绕它的最长边旋转一周,得到的几何体是( C )
11.如图,正方形ABCD的边长为2,将正方形绕直线l旋转一周,所得圆柱从正面看得到的平面图形的周长为多少
解:因为该圆柱从正面看是一个长为4、宽为2的长方形,所以它的周长为12.
【知能提升】
一、选择题
1.【2022洛阳期末】“枪挑一条线,棍扫一大片”,从数学的角度分别解释为( A )
A.点动成线,线动成面 B.线动成面,面动成体
C.点动成线,面动成体 D.点动成面,面动成线
2.下列说法:①圆柱由3个面围成,这3个面都是平的;②圆锥由2个面围成,这2个面中,1个是平的,1个是曲的;③球仅由1个面围成,这个面是平的;④正方体由6个面围成,这6个面都是平的.其中正确的为( C )
A.①② B.②③ C.②④ D.③④
3.若一个棱柱有12个顶点,则下列说法中正确的是 ( C )
A.这个棱柱有5个侧面 B.这个棱柱有5条侧棱
C.这个棱柱的底面是六边形 D.这个棱柱是一个十二棱柱
4.有下列说法:①一点在平面内运动的过程中,能形成一条线段;②一条线段在平面内运动的过程中,能形成一个平行四边形;③一个三角形在空间内运动的过程中,能形成一个三棱柱;④一个圆形在空间内平移的过程中,能形成一个球体.其中正确的是( B )
A.①②③④ B.①②③ C.②③④ D.①③④
5.下列选项的立体图形,不能由一个平面图形经过旋转得到的是( D )
【解析】A项,可由长方形经过旋转得到;B项,可由直角三角形经过旋转得到;C项,可由半圆经过旋转得到;D项,不能由一个平面图形经过旋转得到.
6.如图,几何体是由图中的哪一图形绕虚线旋转一周得到的( D )
A B C D
7.如图,CD是直角三角形ABC的高,将直角三角形ABC按以下方式旋转一周可以得到右侧几何体的是( B )
A.绕着AC旋转 B.绕着AB旋转 C.绕着CD旋转 D.绕着BC旋转
8.【2022营口期末】如图,把左边的长方形绕着给定的直线旋转一周形成的立体图形是( D )
9.将如图所示的图形绕着给定的直线旋转一周后所形成的几何体是( D )
10.圆柱是由长方形绕着它的一边所在直线旋转一周得到的,那么下列四个选项绕直线旋转一周,可以得到如图所示的立体图形的是( A )
二、填空题
11.如图的几何体由 1个曲面和 4 个平面组成,面与面相交成的线中有 7 条是直线, 2 条是曲线,有 6 个顶点.
第11题图 第13题图
12.【武汉武昌区月考】将一个长为5 cm,宽为4 cm的长方形绕它的一边所在的直线旋转一周得到一个几何体,则这个几何体的体积为80π或100π cm3.
13.将棱长为2的正方体毛坯的一角挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 24 .
14.【2021青岛黄岛区月考】将一块直角三角板ABC绕它的一边旋转,旋转后所得的几何体可能是下面图中的 .
【答案】(2)(3)(4)
【解析】以AC边所在的直线为轴,旋转一周形成题图(2)的圆锥体;以BC边所在的直线为轴,旋转一周形成题图(3)的圆锥体;以AB边所在的直线为轴,旋转一周形成题图(4)的立体图形.
三、解答题
15.如图,将一个长方形在直线m上翻滚,请用圆规在图中作出点A所经过的路径.
【解析】由题意可知,A点所经过的路径是先以长方形的长为半径,旋转90°,再以长方形的对角线为半径,旋转90°所对应的弧长.
【答案】
16.如图是一个长为4 cm、宽为3 cm的长方形纸片,该长方形纸片分别绕长、宽所在直线旋转一周(如图1,图2).请你通过计算,说明哪种方式得到的几何体的体积较大.(结果保留π)
解:绕长边旋转得到的圆柱的底面半径为3 cm、高为4 cm,体积为π×32×4=36π(cm3);
绕短边旋转得到的圆柱的底面半径为4 cm、高为3 cm,体积为π×42×3=48π(cm3).
因此绕短边旋转得到的圆柱的体积较大.
17.求图中阴影部分的面积.(单位:cm)
解:图中两个正方形的面积之和为S1=8×8+5×5=89(cm2),
空白部分的面积之和为S2=×(8+5)×5=64.5(cm2),
所以阴影部分的面积为S=S1-S2=89-64.5=24.5(cm2).
18.如图所示,左边是小颖的圆柱形的笔筒,右边是小彬的六棱柱形的笔筒.仔细观察两个笔筒,并回答下面问题.
(1)圆柱、六棱柱各由几个面组成 它们都是平的吗
(2)圆柱形笔筒的侧面与下底面相交成几条线 它(们)是直的吗
(3)六棱柱有几个顶点 经过每个顶点有几条棱
(4)试写出圆柱与棱柱的相同点与不同点.
解:(1)圆柱由3个面组成,六棱柱由8个面组成,圆柱有2个平面,1个曲面,六棱柱的8个面都是平面.
(2)圆柱形笔筒的侧面与下底面相交形成1条线,是曲线.
(3)六棱柱共有12个顶点,经过每个顶点有3条棱.
(4)棱柱与圆柱的相同点:都是柱体.
不同点:棱柱与圆柱的底面形状不同,棱柱的底面是多边形,圆柱的底面是圆形,圆柱的侧面是曲面,而棱柱的侧面是长方形.(答案不唯一,合理即可)
19.新年晚会是我们最欢乐的时候.会场上悬挂着五彩缤纷的小装饰,其中有各种各样的立体图形.
(1)数一下每一个多面体具有的顶点数(V)、棱数(E)和面数(F),并且把结果记入表中:
多面体 顶点数(V) 面数(F) 棱数(E)
正四面体 4 4 6
正方体 8 6 12
正八面体 6 8 12
正十二面体 20 12 30
正二十面体 12 20 30
(2)观察表中的数据,猜想多面体的顶点数(V)、面数(F)和棱数(E)之间的关系.
(3)18世纪瑞士数学家欧拉证明了这一令人惊叹的关系式,即欧拉公式.若已知一个多面体的顶点数V=196,棱的条数E=294,请你用欧拉公式求出这个多面体的面数.
解:(2)因为4+4-6=2,8+6-12=2,6+8-12=2,20+12-30=2,12+20-30=2,所以V+F-E=2.
(3)由V+F-E=2,得196+F-294=2,则F=100,所以这个多面体的面数为100.
