人教版九年级上册25.3用频率估计概率(第1课时)课件(共18张PPT)
文档属性
| 名称 | 人教版九年级上册25.3用频率估计概率(第1课时)课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 16:52:41 | ||
图片预览






文档简介
(共18张PPT)
25.3用频率估计概率(第1课时)
第二十五章 概率初步
学习目标
1.知道通过大量重复试验,可以用频率估计概率;了解频率与概率的区别
2.经历抛掷硬币试验的过程,对数据进行收集整理、描述与分析,体验频率的随机性与规律性,了解用频率估计概率的合理性与必要性,培养随机观念.
3.培养动手能力和处理数据的能力及理性精神和合作精神.
01
新课导入
新课导入
1.抛掷一枚硬币,正面向上的概率是多少?
2.抛掷一枚硬币100次是否会50次正面向上,50次反面向上呢?
0.5
02
探索新知
试验
把全班同学分成10组,每组同学抛掷一枚硬币50次,整理同学们获得的试验数据,并完成如下表格
抛掷次数n 50 100 150 200 250 300 350 400 450 500
“正面向上”的次数m
“正面向上”的频率
请问同学们根据试验所得数据想一想:“正面向上”的频率有什么规律?
试验
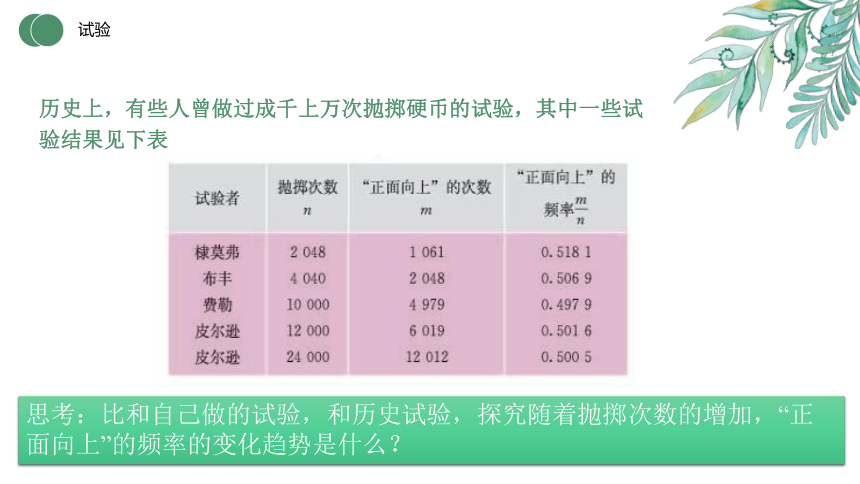
思考:比和自己做的试验,和历史试验,探究随着抛掷次数的增加,“正面向上”的频率的变化趋势是什么?
历史上,有些人曾做过成千上万次抛掷硬币的试验,其中一些试验结果见下表
试验
思考:比和自己做的试验,和历史试验,探究随着抛掷次数的增加,“正面向上”的频率的变化趋势是什么?
可以发现,在重复抛掷一枚硬币时,“正面向上”的频率在0.5附近摆动.
一般地,随着抛掷次数的增加,频率呈现出一定的稳定性:在0.5附近摆动的幅度会越来越小.
这时,我们称“正面向上”的频率稳定于0.5.它与前面用列举法得出的“正面向上”的概率是用一个值.
思考
雅各布·伯努利
瑞士数学家雅各布·伯努利(1654—1705)最早阐明了可以由频率估计概率,即在相同的条件下,大量重复试验时,根据一个随机事件发生的频率所逐渐稳定的常数,可以估计这个事件发生的概率.
思考
点击此处添加标题
用频率估计概率,虽然不像列举法能确切地计算出随机事件的概率,但由于不受“各种结果出现的可能性相等”的条件限制,使得可求概率的随机事件的范围扩大.例如,拋郑一枚图钉或一枚质地不均匀的骰子,不能用列举法求“针尖朝上”或“出现6点”的概率,但可以通过大量重复试验估计出它们的概率
思考
从抛掷硬币的试验还可以发现,“正面向上”的概率是0.5,连续掷2次,结果
不一定是“正面向上”和“反面向上”各1次
连续抛掷100次,结果
也不一定是“正面向上”和“反面向上”各50次
思考
也就是说,概率是0.5并不能保证掷2n次硬币一定恰好有n次“正面向上”,只是当n越来越大时,正面向上的频率会越来越稳定于0.5.可见,概率是针对大量重复试验而言的,大量重复试验反映的规律并非在每一次试验中都发生.
03
练习
练习1
下表记录了一名球员在罚球线上投篮的结果
投篮次数n 50 100 150 200 250 300 500
投中次数m 28 60 78 104 123 152 251
投中频率
(1)计算投中频率(结果保留小数点后两位)
(2)这名球员投篮一次,投中的概率约是多少(结果保留小数点后一位)
可以估计这名球员投篮一次,投中的概率约是0.5
0.56
0.60
0.52
0.52
0.49
0.51
0.50
练习2
全班同学分组做掷骰子的试验,估计掷一次骰子时,“点数是1”的概率.
抛掷次数n 100 200 300 400 500 600 700 800 900 1000
“点数是1”次数m
点数是1”频率
04
小结
小结
谈一谈对频率与概率的关系的认识
结论:在相同条件下,当试验次数很大时,一次随机事件发生的频率会稳定在相应的频率附近.我们可以通过大量重复试验,用一个随机事件发生的频率来估计这一事件发生的概率
谢谢观看
XIEXIEGUANKAN
25.3用频率估计概率(第1课时)
第二十五章 概率初步
学习目标
1.知道通过大量重复试验,可以用频率估计概率;了解频率与概率的区别
2.经历抛掷硬币试验的过程,对数据进行收集整理、描述与分析,体验频率的随机性与规律性,了解用频率估计概率的合理性与必要性,培养随机观念.
3.培养动手能力和处理数据的能力及理性精神和合作精神.
01
新课导入
新课导入
1.抛掷一枚硬币,正面向上的概率是多少?
2.抛掷一枚硬币100次是否会50次正面向上,50次反面向上呢?
0.5
02
探索新知
试验
把全班同学分成10组,每组同学抛掷一枚硬币50次,整理同学们获得的试验数据,并完成如下表格
抛掷次数n 50 100 150 200 250 300 350 400 450 500
“正面向上”的次数m
“正面向上”的频率
请问同学们根据试验所得数据想一想:“正面向上”的频率有什么规律?
试验
思考:比和自己做的试验,和历史试验,探究随着抛掷次数的增加,“正面向上”的频率的变化趋势是什么?
历史上,有些人曾做过成千上万次抛掷硬币的试验,其中一些试验结果见下表
试验
思考:比和自己做的试验,和历史试验,探究随着抛掷次数的增加,“正面向上”的频率的变化趋势是什么?
可以发现,在重复抛掷一枚硬币时,“正面向上”的频率在0.5附近摆动.
一般地,随着抛掷次数的增加,频率呈现出一定的稳定性:在0.5附近摆动的幅度会越来越小.
这时,我们称“正面向上”的频率稳定于0.5.它与前面用列举法得出的“正面向上”的概率是用一个值.
思考
雅各布·伯努利
瑞士数学家雅各布·伯努利(1654—1705)最早阐明了可以由频率估计概率,即在相同的条件下,大量重复试验时,根据一个随机事件发生的频率所逐渐稳定的常数,可以估计这个事件发生的概率.
思考
点击此处添加标题
用频率估计概率,虽然不像列举法能确切地计算出随机事件的概率,但由于不受“各种结果出现的可能性相等”的条件限制,使得可求概率的随机事件的范围扩大.例如,拋郑一枚图钉或一枚质地不均匀的骰子,不能用列举法求“针尖朝上”或“出现6点”的概率,但可以通过大量重复试验估计出它们的概率
思考
从抛掷硬币的试验还可以发现,“正面向上”的概率是0.5,连续掷2次,结果
不一定是“正面向上”和“反面向上”各1次
连续抛掷100次,结果
也不一定是“正面向上”和“反面向上”各50次
思考
也就是说,概率是0.5并不能保证掷2n次硬币一定恰好有n次“正面向上”,只是当n越来越大时,正面向上的频率会越来越稳定于0.5.可见,概率是针对大量重复试验而言的,大量重复试验反映的规律并非在每一次试验中都发生.
03
练习
练习1
下表记录了一名球员在罚球线上投篮的结果
投篮次数n 50 100 150 200 250 300 500
投中次数m 28 60 78 104 123 152 251
投中频率
(1)计算投中频率(结果保留小数点后两位)
(2)这名球员投篮一次,投中的概率约是多少(结果保留小数点后一位)
可以估计这名球员投篮一次,投中的概率约是0.5
0.56
0.60
0.52
0.52
0.49
0.51
0.50
练习2
全班同学分组做掷骰子的试验,估计掷一次骰子时,“点数是1”的概率.
抛掷次数n 100 200 300 400 500 600 700 800 900 1000
“点数是1”次数m
点数是1”频率
04
小结
小结
谈一谈对频率与概率的关系的认识
结论:在相同条件下,当试验次数很大时,一次随机事件发生的频率会稳定在相应的频率附近.我们可以通过大量重复试验,用一个随机事件发生的频率来估计这一事件发生的概率
谢谢观看
XIEXIEGUANKAN
同课章节目录
