人教版数学九年级上册 25.2用列举法求概率(第2课时)教案
文档属性
| 名称 | 人教版数学九年级上册 25.2用列举法求概率(第2课时)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 233.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 07:25:59 | ||
图片预览

文档简介
第二十五章 概率初步
25.2用列举法求概率(第2课时)
教学设计
一、教学目标
1.使学生理解用列举法(画树状图法)求随机事件的概率的方法,进一步培养学生的随机观念.
2.使学生经历用列举法求简单随机事件的概率的过程,体会“分步”策略对解决复杂问题所起到的重要作用.
3.在探究过程中,培养学生有条理地思考问题的能力和增强应用数学的意识.
二、教学重难点
1. 教学重点
用画树状图法求简单随机事件的概率
2. 教学难点
如何画树状图
三、教学过程
(一)新课导入
提出问题
1.同时抛掷两枚硬币,两枚硬币全部正面向上的概率是
(学生回答:正面向上的概率是)
2.若同时抛掷三枚硬币,试列举出所有的试验结果.
学生用列表法列举时会遇到困难,顺势引入画树状图法.
(二)探索新知
活动
同时抛掷三枚硬币,求下列事件的概率:
(1)三枚硬币全部正面向上;
(2)两枚硬币正面向上、一枚硬币反面向上;
(3)至少有两枚硬币正面向上.
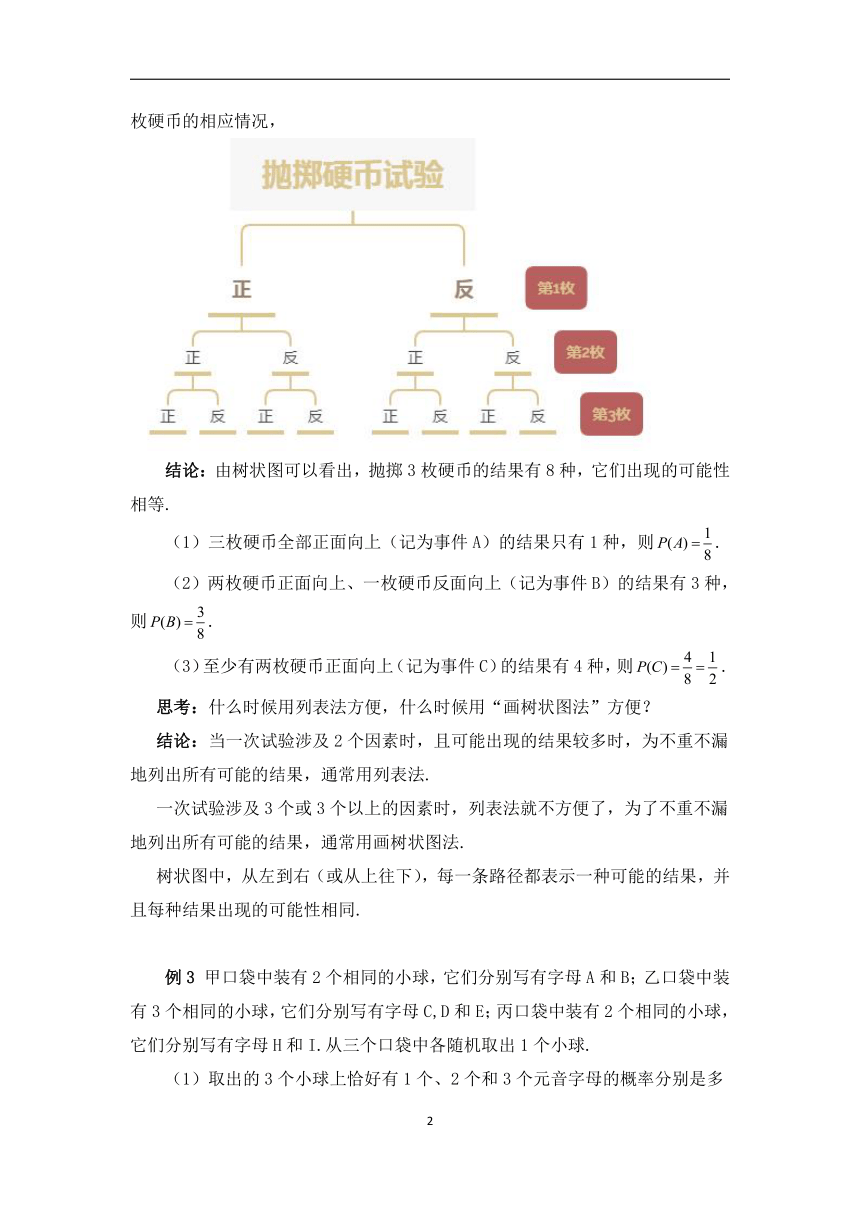
教师引导学生先画出第1枚硬币的两种情况,然后在依次画出第2枚和第3枚硬币的相应情况,
结论:由树状图可以看出,抛掷3枚硬币的结果有8种,它们出现的可能性相等.
(1)三枚硬币全部正面向上(记为事件A)的结果只有1种,则.
(2)两枚硬币正面向上、一枚硬币反面向上(记为事件B)的结果有3种,则.
(3)至少有两枚硬币正面向上(记为事件C)的结果有4种,则.
思考:什么时候用列表法方便,什么时候用“画树状图法”方便?
结论:当一次试验涉及2个因素时,且可能出现的结果较多时,为不重不漏地列出所有可能的结果,通常用列表法.
一次试验涉及3个或3个以上的因素时,列表法就不方便了,为了不重不漏地列出所有可能的结果,通常用画树状图法.
树状图中,从左到右(或从上往下),每一条路径都表示一种可能的结果,并且每种结果出现的可能性相同.
例3 甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C,D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从三个口袋中各随机取出1个小球.
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2)取出的3个小球全是辅音字母的概率是多少?
分析:当一次试验是从三个口袋中取球时,列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用画树状图法.
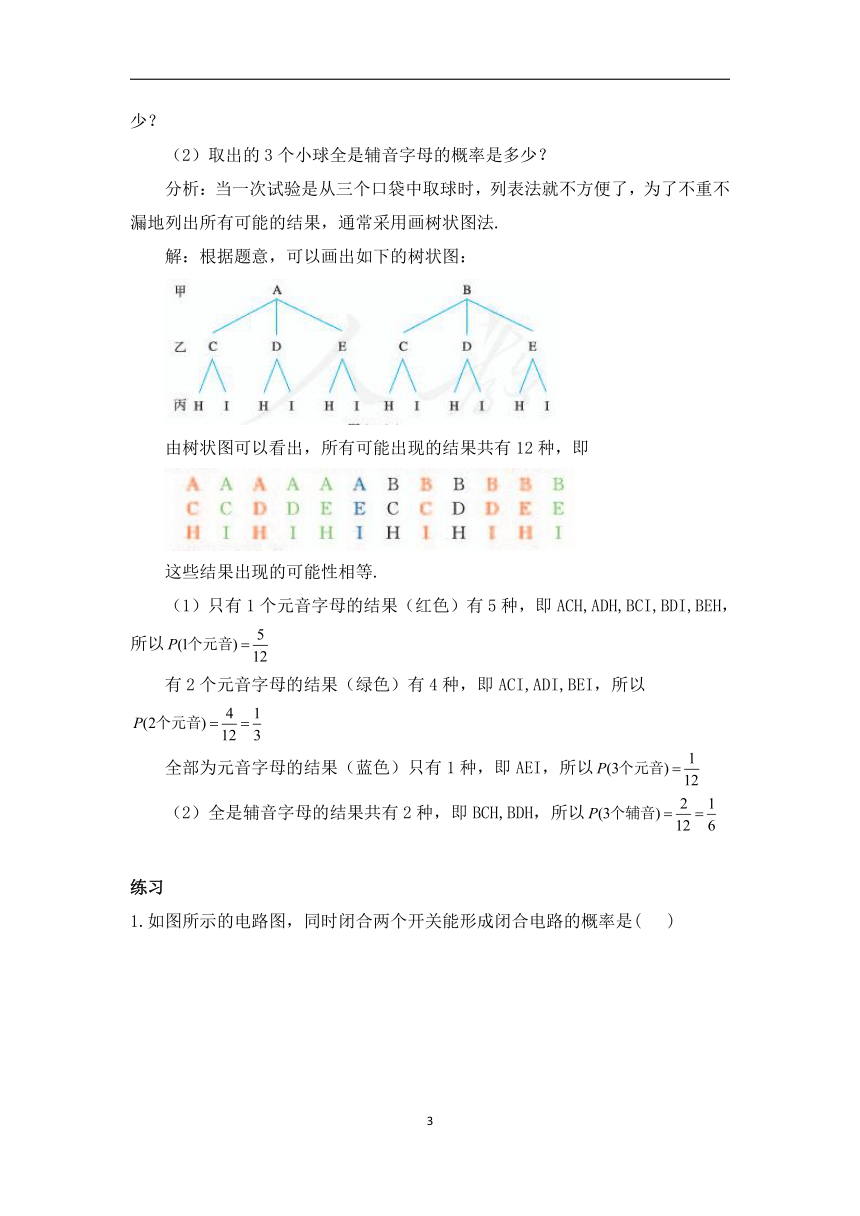
解:根据题意,可以画出如下的树状图:
由树状图可以看出,所有可能出现的结果共有12种,即
这些结果出现的可能性相等.
(1)只有1个元音字母的结果(红色)有5种,即ACH,ADH,BCI,BDI,BEH,所以
有2个元音字母的结果(绿色)有4种,即ACI,ADI,BEI,所以
全部为元音字母的结果(蓝色)只有1种,即AEI,所以
(2)全是辅音字母的结果共有2种,即BCH,BDH,所以
练习
1.如图所示的电路图,同时闭合两个开关能形成闭合电路的概率是( )
A. B. C. D.1
答案:B
解析:把、、分别记为A、B、C,画树状图如下:
共有6种等可能的结果,其中同时闭合两个开关能形成闭合电路的结果有4种,即AB、AC、BA、CA,同时闭合两个开关能形成闭合电路的概率为,故选:B.
2.在一个不透明的袋子里装有两个黄球和一个白球,它们除颜色外都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球.两次都摸到黄球的概率是( )
A. B. C. D.
答案:A
解析:根据题意画出树状图,由树状图求得所有等可能的结果与两次都摸到黄球的结果然后利用概率公式求解画树状图如下:
由树状图可知,共有9种等可能的结果,其中两次都摸到黄球的结果有4种,
两次都摸到黄球的概率为,故选A.
3.如图,小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
A. B. C. D.
答案:A
解析:画树状图如下:
∴共有25种等可能的结果,其中两人出拳的手指数之和为偶数的结果有13种,∴小李获胜的概率为.
4.经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,辆向左转的概率是( )
A. B. C. D.
答案:B
解析:画树状图如图所示:
这两辆汽车的行驶方向共有9种等可能的结果其中一辆向右转,
一辆向左转的结果有2种,
一辆向右转,一辆向左转的概率为.故选B.
(三)小结作业
小结:(学生思考总结,老师适时引导)
1.用列表法或画树状图法求概率时,应注意各种结果出现的可能性务必相同,其目的是保证列举的不重不漏.
2.当试验包含两步时,列表法较方便,当然也可以用画树状图法;如果试验步骤是三步或三步以上,采用画树状图法较为方便,此时难以用列表法.
3.用列表法和画树状图法求概率体现了数形结合及分类的思想,我们常常借助分类的方法把复杂问题转化为简单问题来解决.
作业:
四、板书设计
25.2用列举法求概率(第2课时)
当一次试验涉及2个因素时,且可能出现的结果较多时,为不重不漏地列出所有可能的结果,通常用列表法.
一次试验涉及3个或3个以上的因素时,列表法就不方便了,为了不重不漏地列出所有可能的结果,通常用画树状图法.
树状图中,从左到右(或从上往下),每一条路径都表示一种可能的结果,并且每种结果出现的可能性相同.
2
25.2用列举法求概率(第2课时)
教学设计
一、教学目标
1.使学生理解用列举法(画树状图法)求随机事件的概率的方法,进一步培养学生的随机观念.
2.使学生经历用列举法求简单随机事件的概率的过程,体会“分步”策略对解决复杂问题所起到的重要作用.
3.在探究过程中,培养学生有条理地思考问题的能力和增强应用数学的意识.
二、教学重难点
1. 教学重点
用画树状图法求简单随机事件的概率
2. 教学难点
如何画树状图
三、教学过程
(一)新课导入
提出问题
1.同时抛掷两枚硬币,两枚硬币全部正面向上的概率是
(学生回答:正面向上的概率是)
2.若同时抛掷三枚硬币,试列举出所有的试验结果.
学生用列表法列举时会遇到困难,顺势引入画树状图法.
(二)探索新知
活动
同时抛掷三枚硬币,求下列事件的概率:
(1)三枚硬币全部正面向上;
(2)两枚硬币正面向上、一枚硬币反面向上;
(3)至少有两枚硬币正面向上.
教师引导学生先画出第1枚硬币的两种情况,然后在依次画出第2枚和第3枚硬币的相应情况,
结论:由树状图可以看出,抛掷3枚硬币的结果有8种,它们出现的可能性相等.
(1)三枚硬币全部正面向上(记为事件A)的结果只有1种,则.
(2)两枚硬币正面向上、一枚硬币反面向上(记为事件B)的结果有3种,则.
(3)至少有两枚硬币正面向上(记为事件C)的结果有4种,则.
思考:什么时候用列表法方便,什么时候用“画树状图法”方便?
结论:当一次试验涉及2个因素时,且可能出现的结果较多时,为不重不漏地列出所有可能的结果,通常用列表法.
一次试验涉及3个或3个以上的因素时,列表法就不方便了,为了不重不漏地列出所有可能的结果,通常用画树状图法.
树状图中,从左到右(或从上往下),每一条路径都表示一种可能的结果,并且每种结果出现的可能性相同.
例3 甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C,D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从三个口袋中各随机取出1个小球.
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2)取出的3个小球全是辅音字母的概率是多少?
分析:当一次试验是从三个口袋中取球时,列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用画树状图法.
解:根据题意,可以画出如下的树状图:
由树状图可以看出,所有可能出现的结果共有12种,即
这些结果出现的可能性相等.
(1)只有1个元音字母的结果(红色)有5种,即ACH,ADH,BCI,BDI,BEH,所以
有2个元音字母的结果(绿色)有4种,即ACI,ADI,BEI,所以
全部为元音字母的结果(蓝色)只有1种,即AEI,所以
(2)全是辅音字母的结果共有2种,即BCH,BDH,所以
练习
1.如图所示的电路图,同时闭合两个开关能形成闭合电路的概率是( )
A. B. C. D.1
答案:B
解析:把、、分别记为A、B、C,画树状图如下:
共有6种等可能的结果,其中同时闭合两个开关能形成闭合电路的结果有4种,即AB、AC、BA、CA,同时闭合两个开关能形成闭合电路的概率为,故选:B.
2.在一个不透明的袋子里装有两个黄球和一个白球,它们除颜色外都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球.两次都摸到黄球的概率是( )
A. B. C. D.
答案:A
解析:根据题意画出树状图,由树状图求得所有等可能的结果与两次都摸到黄球的结果然后利用概率公式求解画树状图如下:
由树状图可知,共有9种等可能的结果,其中两次都摸到黄球的结果有4种,
两次都摸到黄球的概率为,故选A.
3.如图,小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
A. B. C. D.
答案:A
解析:画树状图如下:
∴共有25种等可能的结果,其中两人出拳的手指数之和为偶数的结果有13种,∴小李获胜的概率为.
4.经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,辆向左转的概率是( )
A. B. C. D.
答案:B
解析:画树状图如图所示:
这两辆汽车的行驶方向共有9种等可能的结果其中一辆向右转,
一辆向左转的结果有2种,
一辆向右转,一辆向左转的概率为.故选B.
(三)小结作业
小结:(学生思考总结,老师适时引导)
1.用列表法或画树状图法求概率时,应注意各种结果出现的可能性务必相同,其目的是保证列举的不重不漏.
2.当试验包含两步时,列表法较方便,当然也可以用画树状图法;如果试验步骤是三步或三步以上,采用画树状图法较为方便,此时难以用列表法.
3.用列表法和画树状图法求概率体现了数形结合及分类的思想,我们常常借助分类的方法把复杂问题转化为简单问题来解决.
作业:
四、板书设计
25.2用列举法求概率(第2课时)
当一次试验涉及2个因素时,且可能出现的结果较多时,为不重不漏地列出所有可能的结果,通常用列表法.
一次试验涉及3个或3个以上的因素时,列表法就不方便了,为了不重不漏地列出所有可能的结果,通常用画树状图法.
树状图中,从左到右(或从上往下),每一条路径都表示一种可能的结果,并且每种结果出现的可能性相同.
2
同课章节目录
