2022-2023学年冀教版八年级上学期开学摸底考试数学试卷A卷(Word版含答案)
文档属性
| 名称 | 2022-2023学年冀教版八年级上学期开学摸底考试数学试卷A卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 512.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览




文档简介
八年级上学期开学考试数学试卷A卷(模拟试卷)
【满分:120分】
一、选择题:(本大题共12小题,每小题3分,共36分,给出的四个选项中,只有一项是符合题目要求的)
1.成人每天维生素D的摄入量约为0.0000046g.将数据0.0000046用科学记数法表示为( )
A. B.
C. D.
2.用代入法解方程组时,可转化为一元一次方程的问题,若消去y,则含x的一元一次方程为( )
A. B.
C. D.
3.如图4-3-2-13,OB是的平分线,OD是的平分线.如果,,则的度数为( )
A. B. C. D.
4.八年级某班级部分同学去植树,若每人平均植树7棵,还剩9棵,若每人平均植树9棵,则有1名同学植树的棵数不到8棵。设同学人数为x,下列列式正确的是( )
A. B.
C. D.
5.为培养青少年的创新意识、动手实践能力、现场应变能力和团队精神,湘潭市举办了第10届青少年机器人竞赛.组委会为每个比赛场地准备了四条腿的桌子和三条腿的凳子共12个,若桌子腿数与凳子腿数的和为40条,则每个比赛场地有几张桌子和几条凳子?设有x张桌子,有y条凳子,根据题意所列方程组正确的是( )
A. B. C. D.
6.若实数在数轴上对应点的位置如图所示,则下列不等式成立的是( )
A. B. C. D.
7.如图,在中,AD和BE是角平分线,其交点为O,若,则的度数是( )
A.33° B.28° C.52° D.48°
8.已知,,则A与B的大小关系为( )
A. B. C. D.不能确定
9.不等式组的整数解的个数为( )
A.2 B.3 C.4 D.5
10.下列计算正确的是( )
A. B. C. D.
11.如图,AD是的中线,点E,F是AD的三等分点,若的面积为,则图中阴影部分的面积为( )
A.5 B.10 C.15 D.20
12.将一副三角板按如图所示的方式放置,下列结论不正确的是( )
A.若,则 B.
C.若,则 D.若,则
二、填空题:(每小题3分,共18分)
13.计算:__________.
14.把多项式分解因式的结果是_________.
15.若关于x的不等式组无解,则a的取值范围为_______.
16.已知关于的方程组的解满足,则k的值为_________.
17.已知a,b为定值,关于x的方程,无论k为何值,它的解总是2.则___.
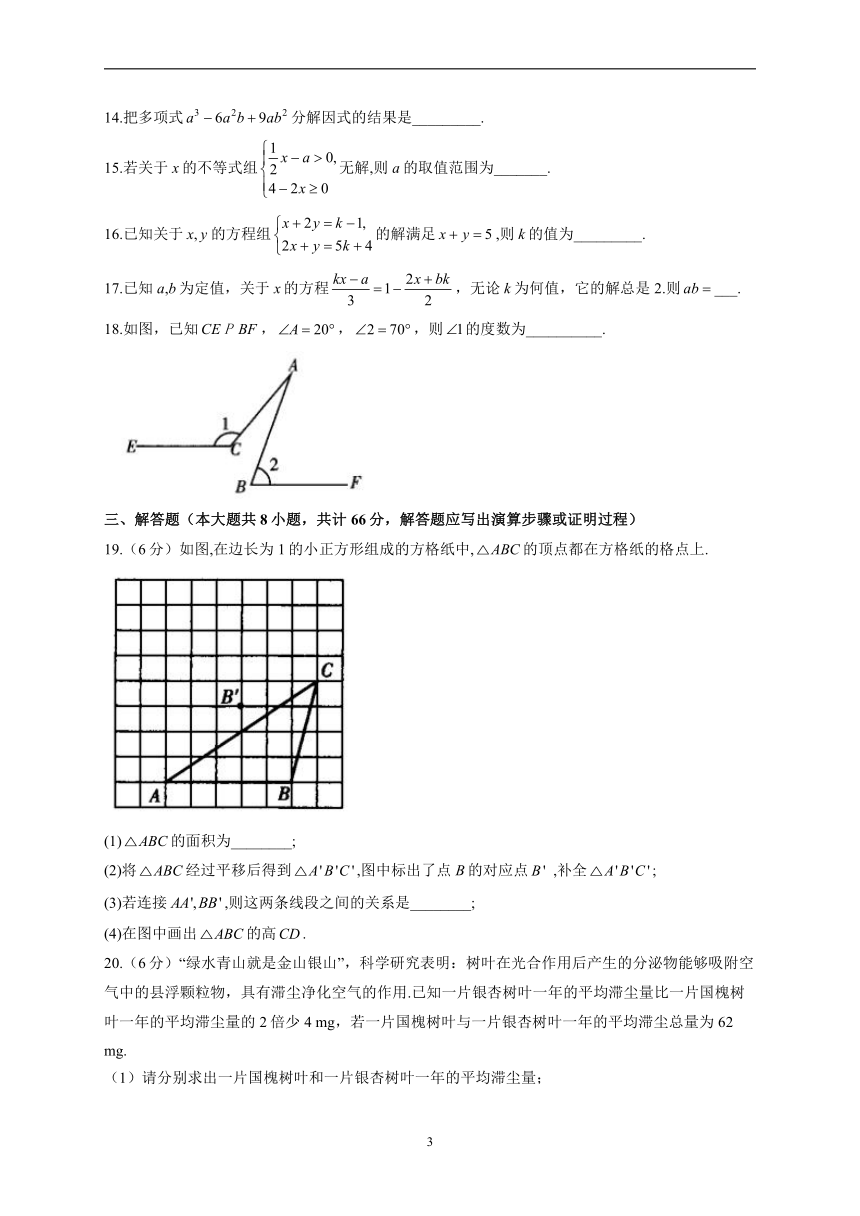
18.如图,已知,,,则的度数为__________.
三、解答题(本大题共8小题,共计66分,解答题应写出演算步骤或证明过程)
19.(6分)如图,在边长为1的小正方形组成的方格纸中,的顶点都在方格纸的格点上.
(1)的面积为________;
(2)将经过平移后得到,图中标出了点B的对应点,补全;
(3)若连接,则这两条线段之间的关系是________;
(4)在图中画出的高.
20.(6分)“绿水青山就是金山银山”,科学研究表明:树叶在光合作用后产生的分泌物能够吸附空气中的县浮颗粒物,具有滞尘净化空气的作用.已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4 mg,若一片国槐树叶与一片银杏树叶一年的平均滞尘总量为62 mg.
(1)请分别求出一片国槐树叶和一片银杏树叶一年的平均滞尘量;
(2)娄底市双峰县九峰山森林公园某处有始于唐代的三棵银杏树,据估计三棵银杏树共有约50000片树叶,问这三棵银杏树一年的平均带尘总量约多少千克?
21.(8分)解不等式组,并把解集在数轴上表示出来.
22.(8分)计算:.
23.(8分)一艘船从甲码头到乙码头顺流而行,用了2 h;从乙码头返回甲码头逆流而行,用了2.5 h,已知水流的速度是3 km/h.
(1)求船在静水中的平均速度;
(2)一个小艇从甲码头到乙码头所用时间是从乙码头到甲码头所用时间的一半,求小艇从甲码头到乙码头所用时间.
24.(8分)如图,在中,平分交的延长线于点,求的度数.
25.(10分)如图,已知
(1)求证:;
(2)若,分别平分,求的度数.
26.(12分)现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.
(1)求A,B两种商品每件各是多少元;
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元,且不低于300元,问有几种购买方案?哪种方案费用最低?
答案以及解析
1.答案:C
解析:.
2.答案:B
解析:由②可得,
再代入①中,可得.
化简,得.故选B.
3.答案:D
解析:是的平分线,.
是的平分线,,
.
,故选D.
4.答案:C
解析:根据题意,得,即.故选C.
5.答案:B
解析:组委会为每个比赛场地准备了桌子和凳子共12个,;又桌子腿数与凳子腿数的和为40条,且每张桌子有4条腿,每条凳子有3条腿,.列出的方程组为.故选:B.
6.答案:B
解析:由题图知,不等式的两边同乘c,得,∴A不符合题意;不等式的两边同乘b,得,∴B符合题意;不等式的两边同加c,得,∴C不符合题意;不等式的两边同加b,得,∴D不符合题意.
7.答案:D
解析:是的外角,,又AD和BE是的角平分线,,,故选D.
8.答案:A
解析:,所以.
9.答案:B
解析:解不等式,得,
解不等式,得,
则不等式组的解集为,
不等式组的整数解为5、6、7,共3个,故选B.
10.答案:B
解析:逐项分析如下:
选项 分析 正误
A ×
B √
C ×
D ×
11.答案:C
解析:因为AD是的中线,所以,所以,,,所以,所以,故选C.
12.答案:C
解析:,又,故A正确,不符合题意;
,故B正确,不符合题意;
,,,故C不正确,符合题意;
,,故D正确,不符合题意.故选C.
13.答案:
解析:原式.
14.答案:
解析:.
15.答案:
解析:解不等式,得.解不等式,得.
∵该不等式组无解,,解得.
16.答案:2
解析:由①+②,得,即.,解得.
17.答案:-4
解析:方程两边都乘6,得,,
整理得,因为无论k为何值,方程的解总是2,
所以,解得,,.
18.答案:130°
解析:方法一:如图(1),过点A作,则,..方法二:如图(2),延长EC交AB于点G. ,.
19.答案:(1)10
(2)
(3)平行且相等
(4)如图所示
解析:(1).
(2)如图所示.
20.答案:(1)一片国槐树叶和一片银杏树叶一年的平均滞尘量分别为22mg,40mg.
(2)这三棵银杏树一年的平均滞尘总量约2千克.
解析:(1)设一片银杏树叶一年的平均滞尘量为x mg,一片国槐树叶一年的平均滞尘量为y mg,
由题意得:,解得:,
答:一片银杏树叶一年的平均滞尘量为40mg,一片国槐树叶一年的平均滞尘量为22mg;
(2)(mg)kg,
答:这三棵银杏树一年的平均滞尘总量约2千克.
21.答案:,图见解析
解析:解:
由①得,
由②得,
该不等式组的解集为,
在数轴上表示该不等式组的解集为:
22.答案:原式
.
23.答案:(1)设船在静水中的平均速度为x km/h.
根据往返路程相等,列方程得,解得.
答:船在静水中的速度为27 km/h.
(2)设小艇在静水中的速度为y km/h,从甲码头到乙码头所用时间为t h.
由题意可得.
因为,所以,解得,
甲、乙码头距离为,
小艇从甲码头到乙码头所用时间为,
答:小艇从甲码头到乙码头所用时间为5 h.
24.答案:在中,,
.
平分,
.
,
.
25.答案:(1)证明:过作,如图,则,
又,
.
(2)过作,如图分别平分
,,
,
26.答案:(1)A种商品每件20元,B种商品每件50元
(2)有两种购买方案,方案一:购买A种商品5件,B种商品5件;方案二:购买A种商品6件,B种商品4件。其中方案二费用最低
解析:(1)设A种商品每件x元,B种商品每件y元.
依题意,得
解得
答:A种商品每件20元,B种商品每件50元.
(2)设小亮准备购买A种商品a件,则购买B种商品件.
依题意,得
解得.
根据题意知,a的值应为整数,所以或.
当时,购买费用为(元);
当时,购买费用为(元).
,
购买A种商品6件,B种商品4件的费用最低.
答:有两种购买方案,方案一:购买A种商品5件,B种商品5件;方案二:购买A种商品6件,B种商品4件.其中方案二费用最低.
2
【满分:120分】
一、选择题:(本大题共12小题,每小题3分,共36分,给出的四个选项中,只有一项是符合题目要求的)
1.成人每天维生素D的摄入量约为0.0000046g.将数据0.0000046用科学记数法表示为( )
A. B.
C. D.
2.用代入法解方程组时,可转化为一元一次方程的问题,若消去y,则含x的一元一次方程为( )
A. B.
C. D.
3.如图4-3-2-13,OB是的平分线,OD是的平分线.如果,,则的度数为( )
A. B. C. D.
4.八年级某班级部分同学去植树,若每人平均植树7棵,还剩9棵,若每人平均植树9棵,则有1名同学植树的棵数不到8棵。设同学人数为x,下列列式正确的是( )
A. B.
C. D.
5.为培养青少年的创新意识、动手实践能力、现场应变能力和团队精神,湘潭市举办了第10届青少年机器人竞赛.组委会为每个比赛场地准备了四条腿的桌子和三条腿的凳子共12个,若桌子腿数与凳子腿数的和为40条,则每个比赛场地有几张桌子和几条凳子?设有x张桌子,有y条凳子,根据题意所列方程组正确的是( )
A. B. C. D.
6.若实数在数轴上对应点的位置如图所示,则下列不等式成立的是( )
A. B. C. D.
7.如图,在中,AD和BE是角平分线,其交点为O,若,则的度数是( )
A.33° B.28° C.52° D.48°
8.已知,,则A与B的大小关系为( )
A. B. C. D.不能确定
9.不等式组的整数解的个数为( )
A.2 B.3 C.4 D.5
10.下列计算正确的是( )
A. B. C. D.
11.如图,AD是的中线,点E,F是AD的三等分点,若的面积为,则图中阴影部分的面积为( )
A.5 B.10 C.15 D.20
12.将一副三角板按如图所示的方式放置,下列结论不正确的是( )
A.若,则 B.
C.若,则 D.若,则
二、填空题:(每小题3分,共18分)
13.计算:__________.
14.把多项式分解因式的结果是_________.
15.若关于x的不等式组无解,则a的取值范围为_______.
16.已知关于的方程组的解满足,则k的值为_________.
17.已知a,b为定值,关于x的方程,无论k为何值,它的解总是2.则___.
18.如图,已知,,,则的度数为__________.
三、解答题(本大题共8小题,共计66分,解答题应写出演算步骤或证明过程)
19.(6分)如图,在边长为1的小正方形组成的方格纸中,的顶点都在方格纸的格点上.
(1)的面积为________;
(2)将经过平移后得到,图中标出了点B的对应点,补全;
(3)若连接,则这两条线段之间的关系是________;
(4)在图中画出的高.
20.(6分)“绿水青山就是金山银山”,科学研究表明:树叶在光合作用后产生的分泌物能够吸附空气中的县浮颗粒物,具有滞尘净化空气的作用.已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4 mg,若一片国槐树叶与一片银杏树叶一年的平均滞尘总量为62 mg.
(1)请分别求出一片国槐树叶和一片银杏树叶一年的平均滞尘量;
(2)娄底市双峰县九峰山森林公园某处有始于唐代的三棵银杏树,据估计三棵银杏树共有约50000片树叶,问这三棵银杏树一年的平均带尘总量约多少千克?
21.(8分)解不等式组,并把解集在数轴上表示出来.
22.(8分)计算:.
23.(8分)一艘船从甲码头到乙码头顺流而行,用了2 h;从乙码头返回甲码头逆流而行,用了2.5 h,已知水流的速度是3 km/h.
(1)求船在静水中的平均速度;
(2)一个小艇从甲码头到乙码头所用时间是从乙码头到甲码头所用时间的一半,求小艇从甲码头到乙码头所用时间.
24.(8分)如图,在中,平分交的延长线于点,求的度数.
25.(10分)如图,已知
(1)求证:;
(2)若,分别平分,求的度数.
26.(12分)现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.
(1)求A,B两种商品每件各是多少元;
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元,且不低于300元,问有几种购买方案?哪种方案费用最低?
答案以及解析
1.答案:C
解析:.
2.答案:B
解析:由②可得,
再代入①中,可得.
化简,得.故选B.
3.答案:D
解析:是的平分线,.
是的平分线,,
.
,故选D.
4.答案:C
解析:根据题意,得,即.故选C.
5.答案:B
解析:组委会为每个比赛场地准备了桌子和凳子共12个,;又桌子腿数与凳子腿数的和为40条,且每张桌子有4条腿,每条凳子有3条腿,.列出的方程组为.故选:B.
6.答案:B
解析:由题图知,不等式的两边同乘c,得,∴A不符合题意;不等式的两边同乘b,得,∴B符合题意;不等式的两边同加c,得,∴C不符合题意;不等式的两边同加b,得,∴D不符合题意.
7.答案:D
解析:是的外角,,又AD和BE是的角平分线,,,故选D.
8.答案:A
解析:,所以.
9.答案:B
解析:解不等式,得,
解不等式,得,
则不等式组的解集为,
不等式组的整数解为5、6、7,共3个,故选B.
10.答案:B
解析:逐项分析如下:
选项 分析 正误
A ×
B √
C ×
D ×
11.答案:C
解析:因为AD是的中线,所以,所以,,,所以,所以,故选C.
12.答案:C
解析:,又,故A正确,不符合题意;
,故B正确,不符合题意;
,,,故C不正确,符合题意;
,,故D正确,不符合题意.故选C.
13.答案:
解析:原式.
14.答案:
解析:.
15.答案:
解析:解不等式,得.解不等式,得.
∵该不等式组无解,,解得.
16.答案:2
解析:由①+②,得,即.,解得.
17.答案:-4
解析:方程两边都乘6,得,,
整理得,因为无论k为何值,方程的解总是2,
所以,解得,,.
18.答案:130°
解析:方法一:如图(1),过点A作,则,..方法二:如图(2),延长EC交AB于点G. ,.
19.答案:(1)10
(2)
(3)平行且相等
(4)如图所示
解析:(1).
(2)如图所示.
20.答案:(1)一片国槐树叶和一片银杏树叶一年的平均滞尘量分别为22mg,40mg.
(2)这三棵银杏树一年的平均滞尘总量约2千克.
解析:(1)设一片银杏树叶一年的平均滞尘量为x mg,一片国槐树叶一年的平均滞尘量为y mg,
由题意得:,解得:,
答:一片银杏树叶一年的平均滞尘量为40mg,一片国槐树叶一年的平均滞尘量为22mg;
(2)(mg)kg,
答:这三棵银杏树一年的平均滞尘总量约2千克.
21.答案:,图见解析
解析:解:
由①得,
由②得,
该不等式组的解集为,
在数轴上表示该不等式组的解集为:
22.答案:原式
.
23.答案:(1)设船在静水中的平均速度为x km/h.
根据往返路程相等,列方程得,解得.
答:船在静水中的速度为27 km/h.
(2)设小艇在静水中的速度为y km/h,从甲码头到乙码头所用时间为t h.
由题意可得.
因为,所以,解得,
甲、乙码头距离为,
小艇从甲码头到乙码头所用时间为,
答:小艇从甲码头到乙码头所用时间为5 h.
24.答案:在中,,
.
平分,
.
,
.
25.答案:(1)证明:过作,如图,则,
又,
.
(2)过作,如图分别平分
,,
,
26.答案:(1)A种商品每件20元,B种商品每件50元
(2)有两种购买方案,方案一:购买A种商品5件,B种商品5件;方案二:购买A种商品6件,B种商品4件。其中方案二费用最低
解析:(1)设A种商品每件x元,B种商品每件y元.
依题意,得
解得
答:A种商品每件20元,B种商品每件50元.
(2)设小亮准备购买A种商品a件,则购买B种商品件.
依题意,得
解得.
根据题意知,a的值应为整数,所以或.
当时,购买费用为(元);
当时,购买费用为(元).
,
购买A种商品6件,B种商品4件的费用最低.
答:有两种购买方案,方案一:购买A种商品5件,B种商品5件;方案二:购买A种商品6件,B种商品4件.其中方案二费用最低.
2
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
