2022-2023学年人教版八年级上学期开学摸底考试数学试卷A卷(word版 含解析)
文档属性
| 名称 | 2022-2023学年人教版八年级上学期开学摸底考试数学试卷A卷(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 626.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 19:50:25 | ||
图片预览

文档简介
八年级上学期开学摸底考试数学试卷A卷(模拟试卷)
【满分:120分】
一、选择题:(本大题共12小题,每小题3分,共36分,给出的四个选项中,只有一项是符合题目要求的)
1.如图所示的图案中,不能由基本图形通过平移变换得到的图案是( )
A. B. C. D.
2.下列各数:(相邻两个2之间0的个数逐次加1),,其中无理数的个数是( )
A.4 B.3 C.2 D.1
3.下列运算中,结果正确的是( )
A. B. C. D.
4.在平面直角坐标系中,点一定不在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
5.方程组的解是( )
A. B. C. D.
6.我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托折回索子来量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺:如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是( )
A. B. C. D.
7.实数在数轴上的对应点如图,则下列各式正确的是( )
A. B. C. D.
8.比较2,,的大小,正确的是( )
A. B. C. D.
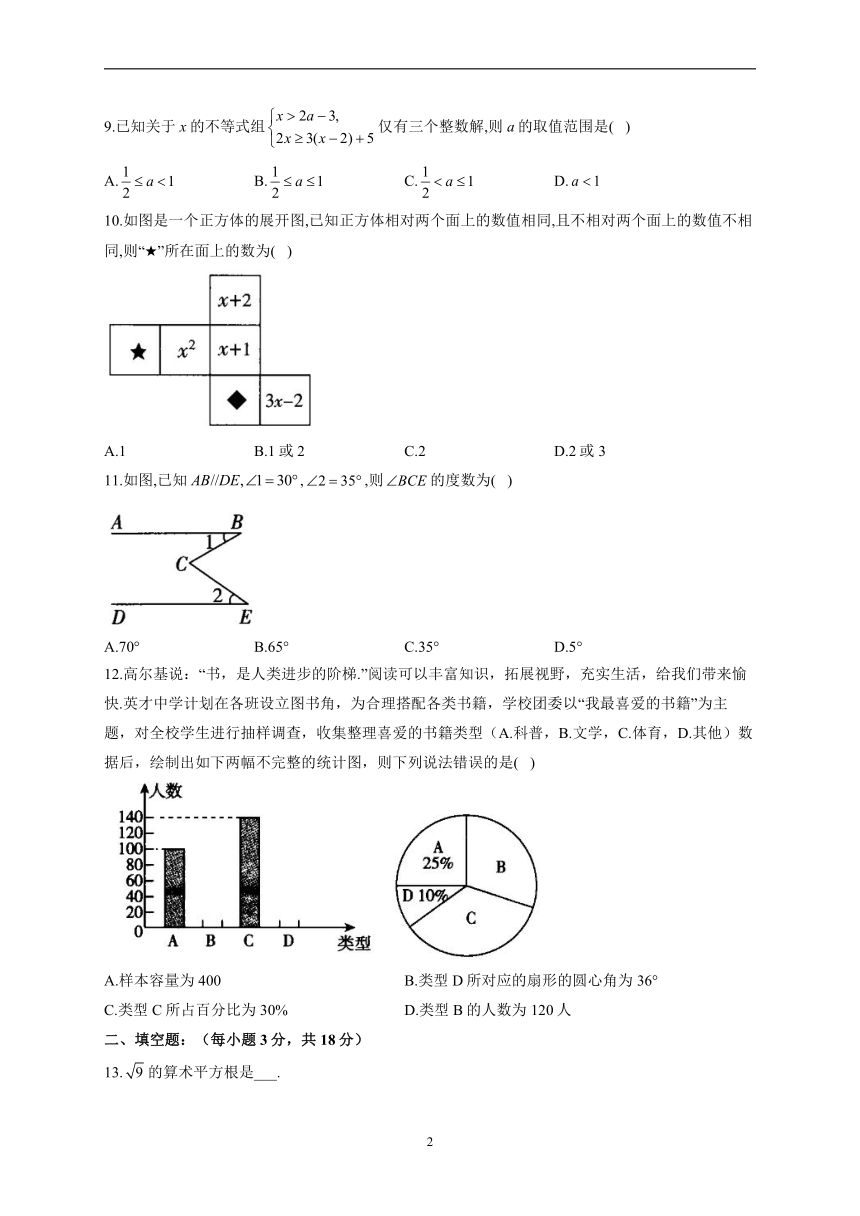
9.已知关于x的不等式组仅有三个整数解,则a的取值范围是( )
A. B. C. D.
10.如图是一个正方体的展开图,已知正方体相对两个面上的数值相同,且不相对两个面上的数值不相同,则“★”所在面上的数为( )
A.1 B.1或2 C.2 D.2或3
11.如图,已知,,则的度数为( )
A.70° B.65° C.35° D.5°
12.高尔基说:“书,是人类进步的阶梯.”阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.英才中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出如下两幅不完整的统计图,则下列说法错误的是( )
A.样本容量为400 B.类型D所对应的扇形的圆心角为36°
C.类型C所占百分比为30% D.类型B的人数为120人
二、填空题:(每小题3分,共18分)
13.的算术平方根是___.
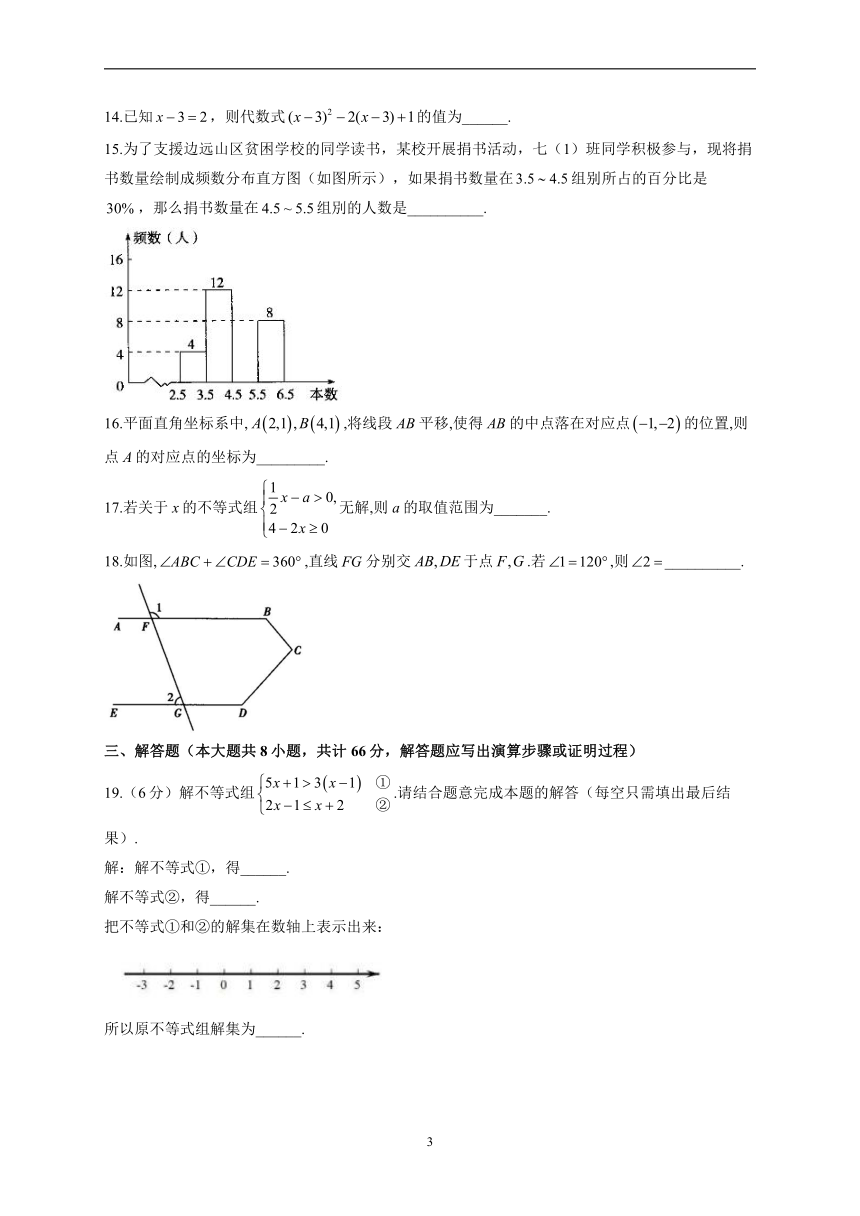
14.已知,则代数式的值为______.
15.为了支援边远山区贫困学校的同学读书,某校开展捐书活动,七(1)班同学积极参与,现将捐书数量绘制成频数分布直方图(如图所示),如果捐书数量在组别所占的百分比是,那么捐书数量在组別的人数是__________.
16.平面直角坐标系中,,将线段平移,使得的中点落在对应点的位置,则点A的对应点的坐标为_________.
17.若关于x的不等式组无解,则a的取值范围为_______.
18.如图,,直线分别交于点.若,则__________.
三、解答题(本大题共8小题,共计66分,解答题应写出演算步骤或证明过程)
19.(6分)解不等式组.请结合题意完成本题的解答(每空只需填出最后结果).
解:解不等式①,得______.
解不等式②,得______.
把不等式①和②的解集在数轴上表示出来:
所以原不等式组解集为______.
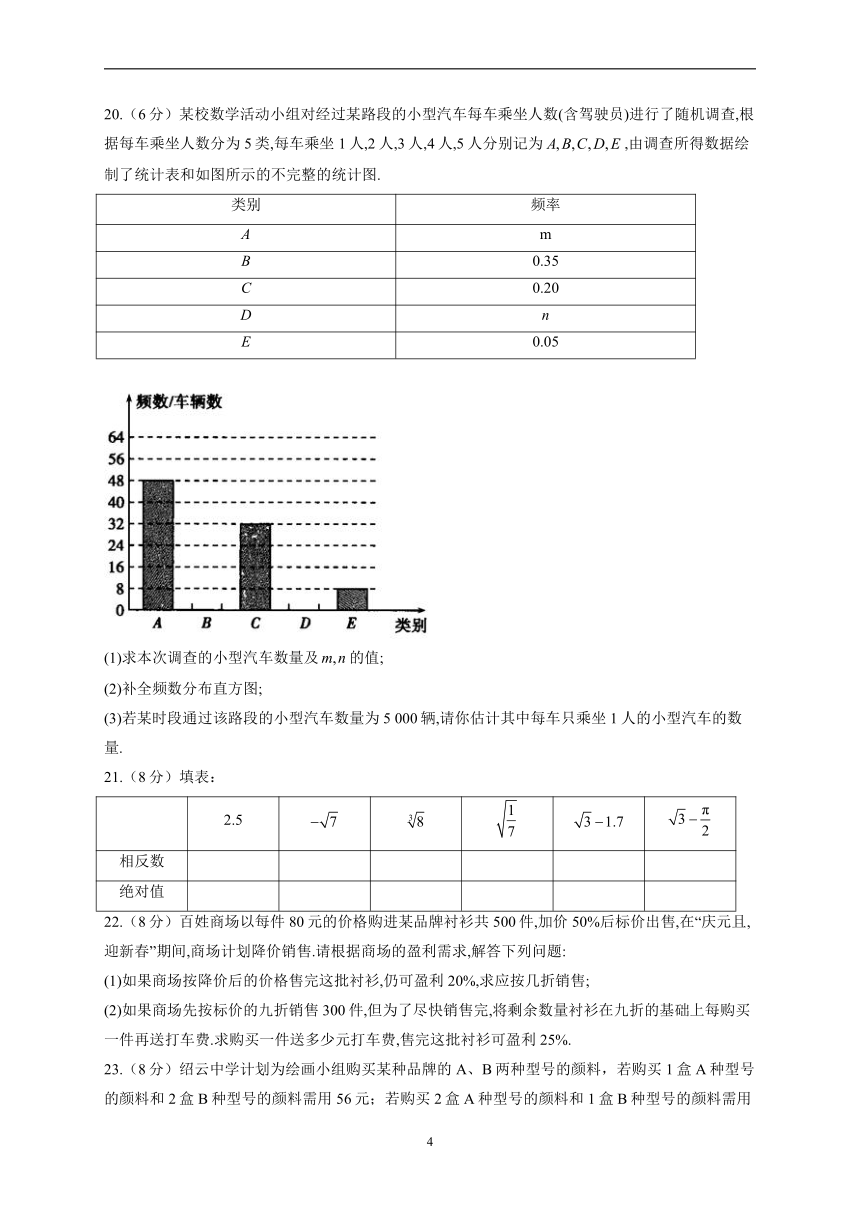
20.(6分)某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数分为5类,每车乘坐1人,2人,3人,4人,5人分别记为,由调查所得数据绘制了统计表和如图所示的不完整的统计图.
类别 频率
A m
B 0.35
C 0.20
D n
E 0.05
(1)求本次调查的小型汽车数量及的值;
(2)补全频数分布直方图;
(3)若某时段通过该路段的小型汽车数量为5 000辆,请你估计其中每车只乘坐1人的小型汽车的数量.
21.(8分)填表:
2.5
相反数
绝对值
22.(8分)百姓商场以每件80元的价格购进某品牌衬衫共500件,加价50%后标价出售,在“庆元且,迎新春”期间,商场计划降价销售.请根据商场的盈利需求,解答下列问题:
(1)如果商场按降价后的价格售完这批衬衫,仍可盈利20%,求应按几折销售;
(2)如果商场先按标价的九折销售300件,但为了尽快销售完,将剩余数量衬衫在九折的基础上每购买一件再送打车费.求购买一件送多少元打车费,售完这批衬衫可盈利25%.
23.(8分)绍云中学计划为绘画小组购买某种品牌的A、B两种型号的颜料,若购买1盒A种型号的颜料和2盒B种型号的颜料需用56元;若购买2盒A种型号的颜料和1盒B种型号的颜料需用64元.
(1)求每盒A种型号的颜料和每盒B种型号的颜料各多少元;
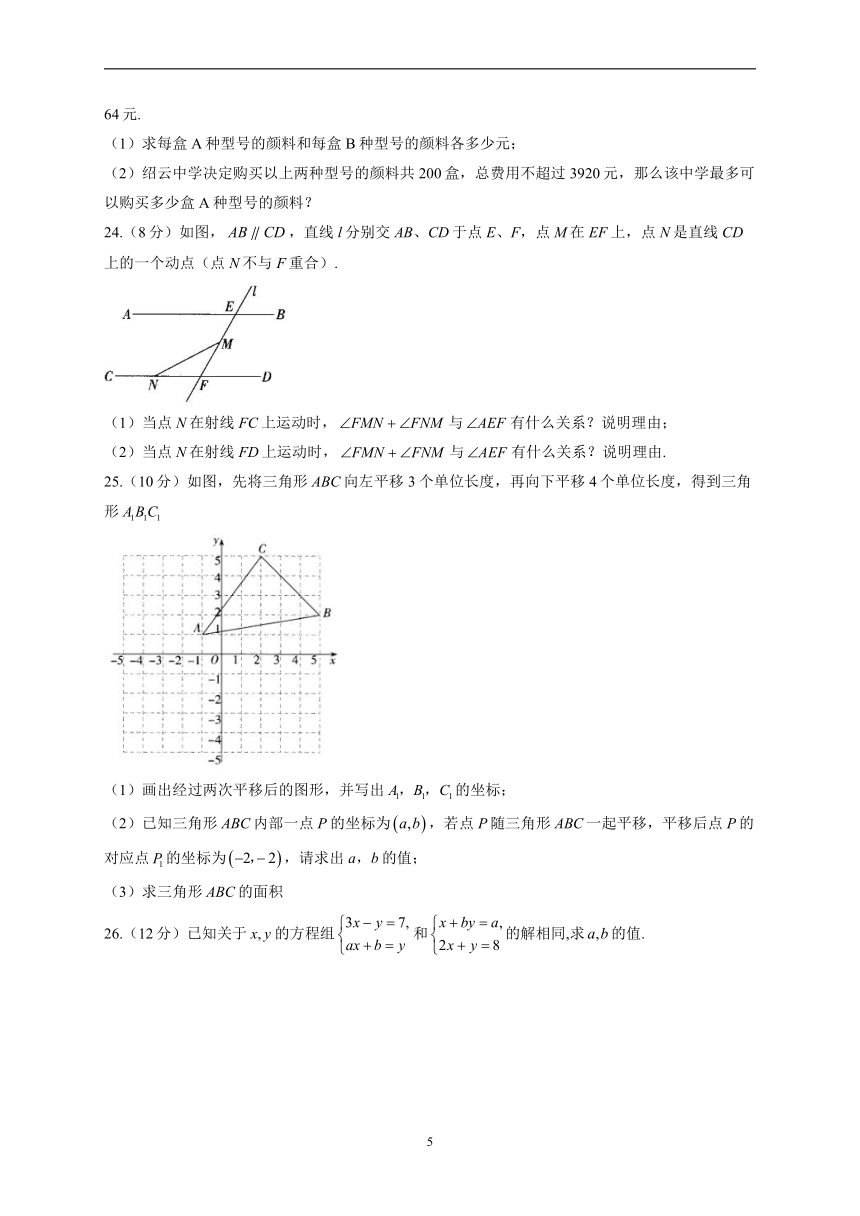
(2)绍云中学决定购买以上两种型号的颜料共200盒,总费用不超过3920元,那么该中学最多可以购买多少盒A种型号的颜料?
24.(8分)如图,,直线l分别交AB、CD于点E、F,点M在EF上,点N是直线CD上的一个动点(点N不与F重合).
(1)当点N在射线FC上运动时,与有什么关系?说明理由;
(2)当点N在射线FD上运动时,与有什么关系?说明理由.
25.(10分)如图,先将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形
(1)画出经过两次平移后的图形,并写出的坐标;
(2)已知三角形ABC内部一点P的坐标为,若点P随三角形ABC一起平移,平移后点P的对应点的坐标为,请求出a,b的值;
(3)求三角形ABC的面积
26.(12分)已知关于的方程组和的解相同,求的值.
答案以及解析
1.答案:B
解析:A、C、D选项中的图案都可以通过基本图形平移得到;
B选项中的图案不能通过基本图形平移得到.故选B.
2.答案:C
解析:无限不循环小数叫做无理数,(相邻两个2之间0的个数逐次加1),π是无理数,注意,它不是无理数.
3.答案:D
解析:选项A、B中的两个相加的单项式不是同类项,不能合并,选项C中,只有选项D是正确的.
4.答案:A
解析:由,可得点P的纵坐标大于横坐标,∵第四象限内的点的坐标特征为,即纵坐标小于横坐标,∴点P一定不在第四象限.
5.答案:A
解析:
得,系数化为1,得,
将代入②,得,
故方程组的解为故选A.
6.答案:A
解析:由“绳索比竿长5尺”可得;由“将绳索对半折后再去量竿,就比竿短5尺”可得.所以符合题意的方程组是
7.答案:C
解析:由图可知,,故A,B,D选项错误,C选项正确.
8.答案:A
解析:,,,,.
9.答案:A
解析:解不等式得,因为不等式组仅有三个整数解,所以这三个整数解为1,0,-1,所以,解此不等式得,故选A.
10.答案:C
解析:题图一个正方体的展开图,共有六个面,其中“”与“”所在面相对,“★”与“”所在面相对.∵相对两个面上的数值相同,,解得或.又∵不相对两个面上的数值不相同,当时,,,,不符合题意,只能为1,则“★”所在面上的数为.故选C.
11.答案:B
解析:如图,过点C作.由题意,得,
.,.
12.答案:C
解析:,故样本容量为400,选项A中的说法正确;类型D所对应的扇形的圆心角为,故选项B中的说法正确;类型C所占百分比为,故选项C中的说法错误;类型B的人数为(人),故选项D中的说法正确.故选C.
13.答案:
解析:的算术平方根是.故答案是.
14.答案:1
解析:.
15.答案:16
解析:捐书数量在组别的频数是12,所占的百分比是,
捐书的总人数为,
捐书数量在组别的人数是.
16.答案:
解析:由可知轴,易知的中点坐标为(3,1),由(3,1)平移到,可知横坐标减4,纵坐标减3,故点A的对应点为,即.
17.答案:
解析:解不等式,得.解不等式,得.
∵该不等式组无解,,解得.
18.答案:60°
解析:如图,过点C作,
则,
,
,
,
,
,
.
19.答案:见解析
解析:解:解不等式①,得,
解不等式②,得,
把不等式①和②的解集在数轴上表示出来为:
所以原不等式组解集为:.
20.答案: (1)0.3;0.1
(2)
(3)1 500
解析: (1)本次调查的小型汽车数量为32÷0.2=160(辆), ,.
(2)B类小型汽车的数量为160×0.35=56(辆),D类小型汽车的数量为0.1×160=16(辆).
补全图形如下:
(3)估计其中每车只乘坐1人的小型汽车的数量为5 000×0.3=1 500(辆).
21.答案:
2.5
相反数 -2.5 -2
绝对值 2.5 2
22.答案:(1)八
(2)20
解析:(1)设应按x折销售.
根据题意,得,解得.
∴应按八折销售.
(2)设购买一件送y元打车费.
根据题意,得,解得.
∴购买一件送20元打车费,售完这批衬衫后可盈利25%.
23.答案:(1)每盒A种型号的颜料24元,每盒B种型号的颜料16元
(2)该中学最多可以购买90盒A种型号的颜料
解析:(1)解:设每盒A种型号的颜料x元,每盒B种型号的颜料y元.
根据题意得解得
每盒A种型号的颜料24元,每盒B种型号的颜料16元.
(2)解:设该中学可以购买a盒A种型号的颜料
根据题意得
解得
该中学最多可以购买90盒A种型号的颜料.
24.答案:(1).
理由:,.
,
.
(2).
理由:如图,,.
,
.
25.答案:(1)见解析
(2),
(3)10.5
解析:(1)如图所示,,
(2)平移后点P的对应点的坐标为,
,
,
,
(3)
26.答案:1,-1
解析:将方程组重新组合,得
由①+②,得,解得.
将代入①,得,解得.
∴方程组的解为
将解代入另两个方程,得
将④代入③,得,解得.
将代入④,解得.
的值为的值为-1.
2
【满分:120分】
一、选择题:(本大题共12小题,每小题3分,共36分,给出的四个选项中,只有一项是符合题目要求的)
1.如图所示的图案中,不能由基本图形通过平移变换得到的图案是( )
A. B. C. D.
2.下列各数:(相邻两个2之间0的个数逐次加1),,其中无理数的个数是( )
A.4 B.3 C.2 D.1
3.下列运算中,结果正确的是( )
A. B. C. D.
4.在平面直角坐标系中,点一定不在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
5.方程组的解是( )
A. B. C. D.
6.我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托折回索子来量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺:如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是( )
A. B. C. D.
7.实数在数轴上的对应点如图,则下列各式正确的是( )
A. B. C. D.
8.比较2,,的大小,正确的是( )
A. B. C. D.
9.已知关于x的不等式组仅有三个整数解,则a的取值范围是( )
A. B. C. D.
10.如图是一个正方体的展开图,已知正方体相对两个面上的数值相同,且不相对两个面上的数值不相同,则“★”所在面上的数为( )
A.1 B.1或2 C.2 D.2或3
11.如图,已知,,则的度数为( )
A.70° B.65° C.35° D.5°
12.高尔基说:“书,是人类进步的阶梯.”阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.英才中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出如下两幅不完整的统计图,则下列说法错误的是( )
A.样本容量为400 B.类型D所对应的扇形的圆心角为36°
C.类型C所占百分比为30% D.类型B的人数为120人
二、填空题:(每小题3分,共18分)
13.的算术平方根是___.
14.已知,则代数式的值为______.
15.为了支援边远山区贫困学校的同学读书,某校开展捐书活动,七(1)班同学积极参与,现将捐书数量绘制成频数分布直方图(如图所示),如果捐书数量在组别所占的百分比是,那么捐书数量在组別的人数是__________.
16.平面直角坐标系中,,将线段平移,使得的中点落在对应点的位置,则点A的对应点的坐标为_________.
17.若关于x的不等式组无解,则a的取值范围为_______.
18.如图,,直线分别交于点.若,则__________.
三、解答题(本大题共8小题,共计66分,解答题应写出演算步骤或证明过程)
19.(6分)解不等式组.请结合题意完成本题的解答(每空只需填出最后结果).
解:解不等式①,得______.
解不等式②,得______.
把不等式①和②的解集在数轴上表示出来:
所以原不等式组解集为______.
20.(6分)某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数分为5类,每车乘坐1人,2人,3人,4人,5人分别记为,由调查所得数据绘制了统计表和如图所示的不完整的统计图.
类别 频率
A m
B 0.35
C 0.20
D n
E 0.05
(1)求本次调查的小型汽车数量及的值;
(2)补全频数分布直方图;
(3)若某时段通过该路段的小型汽车数量为5 000辆,请你估计其中每车只乘坐1人的小型汽车的数量.
21.(8分)填表:
2.5
相反数
绝对值
22.(8分)百姓商场以每件80元的价格购进某品牌衬衫共500件,加价50%后标价出售,在“庆元且,迎新春”期间,商场计划降价销售.请根据商场的盈利需求,解答下列问题:
(1)如果商场按降价后的价格售完这批衬衫,仍可盈利20%,求应按几折销售;
(2)如果商场先按标价的九折销售300件,但为了尽快销售完,将剩余数量衬衫在九折的基础上每购买一件再送打车费.求购买一件送多少元打车费,售完这批衬衫可盈利25%.
23.(8分)绍云中学计划为绘画小组购买某种品牌的A、B两种型号的颜料,若购买1盒A种型号的颜料和2盒B种型号的颜料需用56元;若购买2盒A种型号的颜料和1盒B种型号的颜料需用64元.
(1)求每盒A种型号的颜料和每盒B种型号的颜料各多少元;
(2)绍云中学决定购买以上两种型号的颜料共200盒,总费用不超过3920元,那么该中学最多可以购买多少盒A种型号的颜料?
24.(8分)如图,,直线l分别交AB、CD于点E、F,点M在EF上,点N是直线CD上的一个动点(点N不与F重合).
(1)当点N在射线FC上运动时,与有什么关系?说明理由;
(2)当点N在射线FD上运动时,与有什么关系?说明理由.
25.(10分)如图,先将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形
(1)画出经过两次平移后的图形,并写出的坐标;
(2)已知三角形ABC内部一点P的坐标为,若点P随三角形ABC一起平移,平移后点P的对应点的坐标为,请求出a,b的值;
(3)求三角形ABC的面积
26.(12分)已知关于的方程组和的解相同,求的值.
答案以及解析
1.答案:B
解析:A、C、D选项中的图案都可以通过基本图形平移得到;
B选项中的图案不能通过基本图形平移得到.故选B.
2.答案:C
解析:无限不循环小数叫做无理数,(相邻两个2之间0的个数逐次加1),π是无理数,注意,它不是无理数.
3.答案:D
解析:选项A、B中的两个相加的单项式不是同类项,不能合并,选项C中,只有选项D是正确的.
4.答案:A
解析:由,可得点P的纵坐标大于横坐标,∵第四象限内的点的坐标特征为,即纵坐标小于横坐标,∴点P一定不在第四象限.
5.答案:A
解析:
得,系数化为1,得,
将代入②,得,
故方程组的解为故选A.
6.答案:A
解析:由“绳索比竿长5尺”可得;由“将绳索对半折后再去量竿,就比竿短5尺”可得.所以符合题意的方程组是
7.答案:C
解析:由图可知,,故A,B,D选项错误,C选项正确.
8.答案:A
解析:,,,,.
9.答案:A
解析:解不等式得,因为不等式组仅有三个整数解,所以这三个整数解为1,0,-1,所以,解此不等式得,故选A.
10.答案:C
解析:题图一个正方体的展开图,共有六个面,其中“”与“”所在面相对,“★”与“”所在面相对.∵相对两个面上的数值相同,,解得或.又∵不相对两个面上的数值不相同,当时,,,,不符合题意,只能为1,则“★”所在面上的数为.故选C.
11.答案:B
解析:如图,过点C作.由题意,得,
.,.
12.答案:C
解析:,故样本容量为400,选项A中的说法正确;类型D所对应的扇形的圆心角为,故选项B中的说法正确;类型C所占百分比为,故选项C中的说法错误;类型B的人数为(人),故选项D中的说法正确.故选C.
13.答案:
解析:的算术平方根是.故答案是.
14.答案:1
解析:.
15.答案:16
解析:捐书数量在组别的频数是12,所占的百分比是,
捐书的总人数为,
捐书数量在组别的人数是.
16.答案:
解析:由可知轴,易知的中点坐标为(3,1),由(3,1)平移到,可知横坐标减4,纵坐标减3,故点A的对应点为,即.
17.答案:
解析:解不等式,得.解不等式,得.
∵该不等式组无解,,解得.
18.答案:60°
解析:如图,过点C作,
则,
,
,
,
,
,
.
19.答案:见解析
解析:解:解不等式①,得,
解不等式②,得,
把不等式①和②的解集在数轴上表示出来为:
所以原不等式组解集为:.
20.答案: (1)0.3;0.1
(2)
(3)1 500
解析: (1)本次调查的小型汽车数量为32÷0.2=160(辆), ,.
(2)B类小型汽车的数量为160×0.35=56(辆),D类小型汽车的数量为0.1×160=16(辆).
补全图形如下:
(3)估计其中每车只乘坐1人的小型汽车的数量为5 000×0.3=1 500(辆).
21.答案:
2.5
相反数 -2.5 -2
绝对值 2.5 2
22.答案:(1)八
(2)20
解析:(1)设应按x折销售.
根据题意,得,解得.
∴应按八折销售.
(2)设购买一件送y元打车费.
根据题意,得,解得.
∴购买一件送20元打车费,售完这批衬衫后可盈利25%.
23.答案:(1)每盒A种型号的颜料24元,每盒B种型号的颜料16元
(2)该中学最多可以购买90盒A种型号的颜料
解析:(1)解:设每盒A种型号的颜料x元,每盒B种型号的颜料y元.
根据题意得解得
每盒A种型号的颜料24元,每盒B种型号的颜料16元.
(2)解:设该中学可以购买a盒A种型号的颜料
根据题意得
解得
该中学最多可以购买90盒A种型号的颜料.
24.答案:(1).
理由:,.
,
.
(2).
理由:如图,,.
,
.
25.答案:(1)见解析
(2),
(3)10.5
解析:(1)如图所示,,
(2)平移后点P的对应点的坐标为,
,
,
,
(3)
26.答案:1,-1
解析:将方程组重新组合,得
由①+②,得,解得.
将代入①,得,解得.
∴方程组的解为
将解代入另两个方程,得
将④代入③,得,解得.
将代入④,解得.
的值为的值为-1.
2
同课章节目录
