2022-2023学年人教版九年级上学期开学摸底考试数学试卷A卷(word版 含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级上学期开学摸底考试数学试卷A卷(word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 674.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览



文档简介
九年级上学期开学摸底考试数学试卷A卷(模拟试卷)
【满分:120分】
一、选择题:(本大题共12小题,每小题3分,共36分,给出的四个选项中,只有一项是符合题目要求的)
1.以下列长度的各组线段为边,能组成三角形的是( )
A.2 cm,3 cm,6 cm B.3 cm,4 cm,8 cm
C.5 cm,6 cm,10 cm D.5 cm,6 cm,11 cm
2.二次根式中x的取值范围是( )
A. B. C. D.
3.若正多边形的内角和是540°,则该正多边形的一个外角为( )
A.45° B.60° C.72° D.90°
4.下列四组数中,是勾股数的是( )
A.0.3,0.4,0.5 B.,, C.3,4,5 D.,,
5.为迎接中国共产党建党一百周年,某班50名同学进行了党史知识竞赛,测试成绩统计如下表,其中有两个数据被遮盖.
成绩/分 91 92 93 94 95 96 97 98 99 100
人数 1 2 3 5 6 8 10 12
下列关于成绩的统计量中,与被遮盖的数据无关的是( )
A.平均数,方差 B.中位数,方差 C.中位数,众数 D.平均数,众数
6.如图,在和中,已知,在不添加任何辅助线的前提下,要使,再添加的一个条件不可以是( )
A. B. C. D.
7.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为CD的中点.若,则菱形ABCD的周长为( )
A.6 B.12 C.24 D.48
8.下列关于一次函数的说法,错误的是( )
A.图象经过第一、二、四象限 B.y随x的增大而减小
C.图象与y轴交于点 D.当,时,
9.已知关于x的分式方程的解是正数,则m的取值范围是( )
A. B. C.且 D.且
10.计算的结果是( )
A.5 B.-5 C.7 D.-7
11.如图,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于的最小值的是( )
A.AB B.DE C.BD D.AF
12.如图,平行四边形ABCD的对角线AC与BD相交于点O,,垂足为E,,,,则AE的长为( )
A. B. C. D.
二、填空题:(每小题3分,共18分)
13.若a是正整数,是最简二次根式,则a的最小值为_____________.
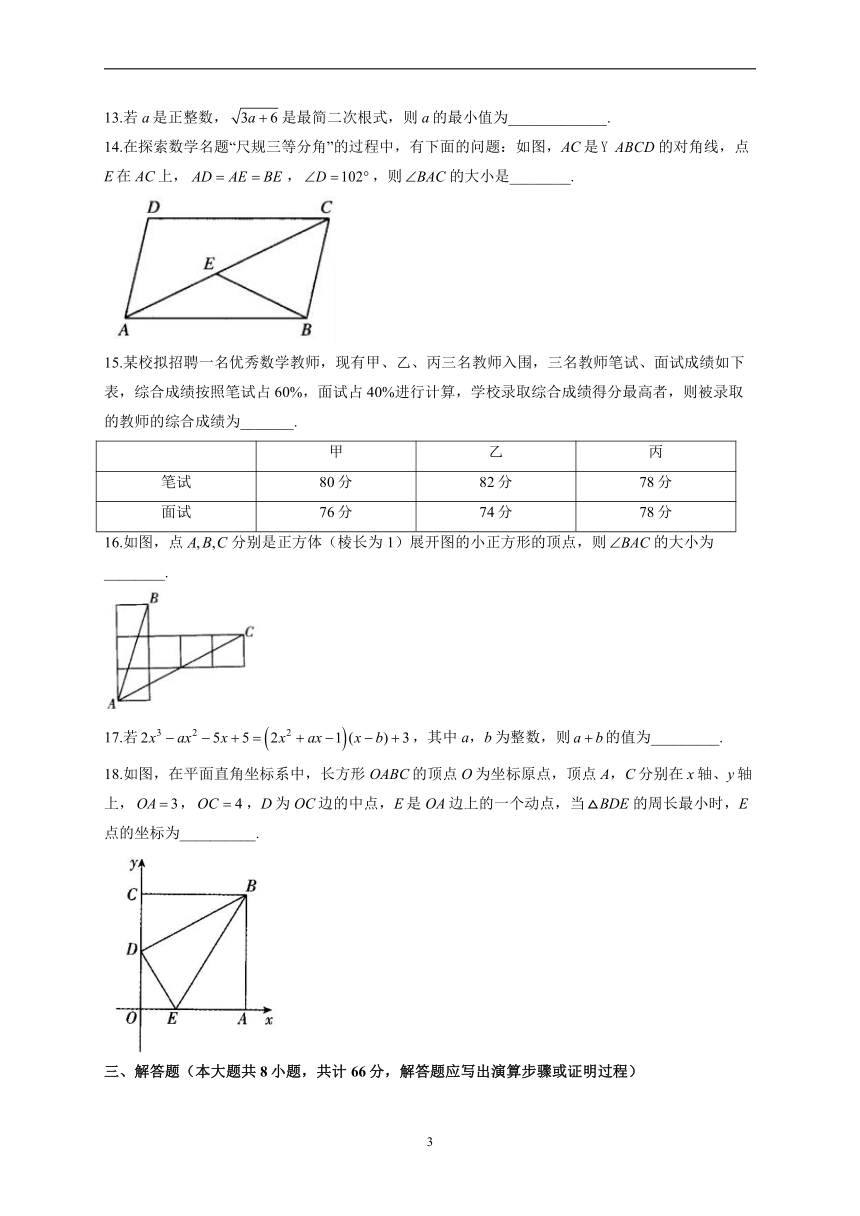
14.在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是的对角线,点E在AC上,,,则的大小是________.
15.某校拟招聘一名优秀数学教师,现有甲、乙、丙三名教师入围,三名教师笔试、面试成绩如下表,综合成绩按照笔试占60%,面试占40%进行计算,学校录取综合成绩得分最高者,则被录取的教师的综合成绩为_______.
甲 乙 丙
笔试 80分 82分 78分
面试 76分 74分 78分
16.如图,点分别是正方体(棱长为1)展开图的小正方形的顶点,则的大小为________.
17.若,其中a,b为整数,则的值为_________.
18.如图,在平面直角坐标系中,长方形OABC的顶点O为坐标原点,顶点A,C分别在x轴、y轴上,,,D为OC边的中点,E是OA边上的一个动点,当的周长最小时,E点的坐标为__________.
三、解答题(本大题共8小题,共计66分,解答题应写出演算步骤或证明过程)
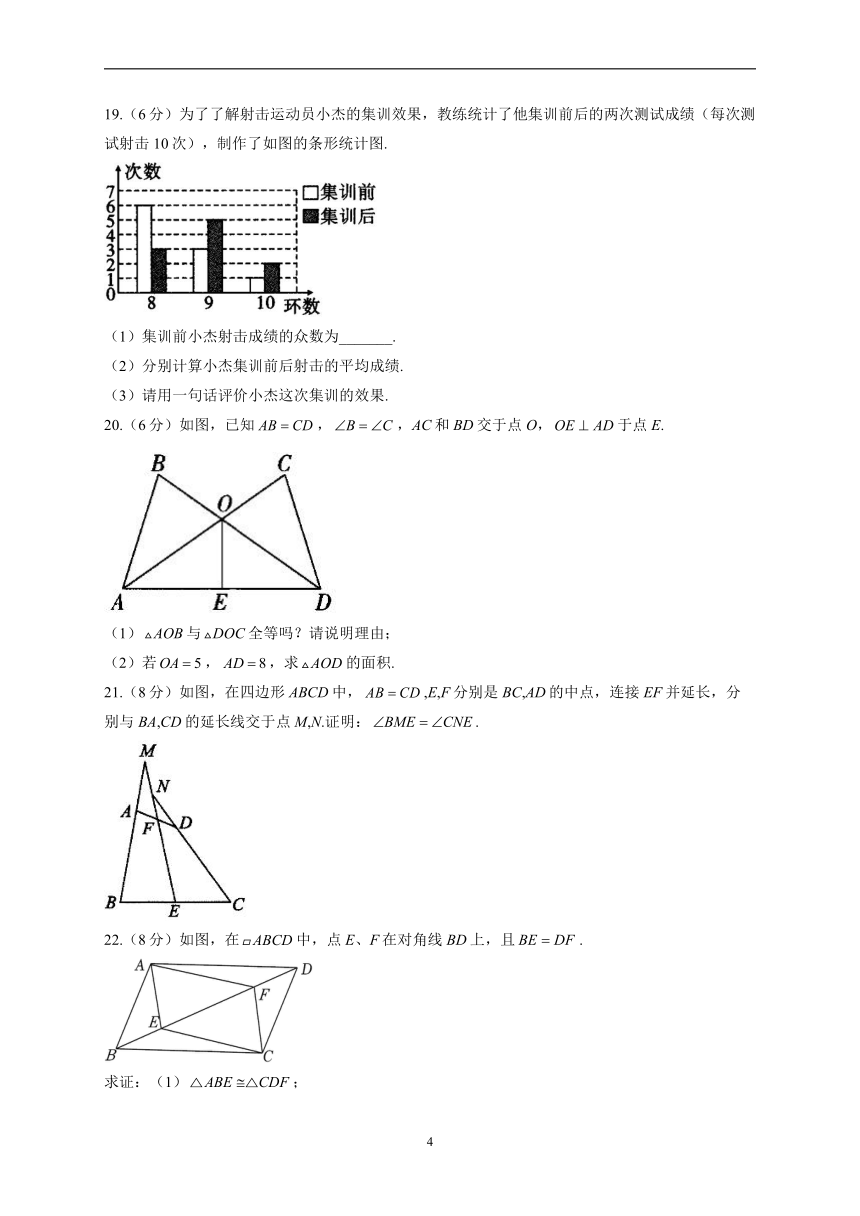
19.(6分)为了了解射击运动员小杰的集训效果,教练统计了他集训前后的两次测试成绩(每次测试射击10次),制作了如图的条形统计图.
(1)集训前小杰射击成绩的众数为_______.
(2)分别计算小杰集训前后射击的平均成绩.
(3)请用一句话评价小杰这次集训的效果.
20.(6分)如图,已知,,AC和BD交于点O,于点E.
(1)与全等吗?请说明理由;
(2)若,,求的面积.
21.(8分)如图,在四边形ABCD中,,E,F分别是BC,AD的中点,连接EF并延长,分别与BA,CD的延长线交于点M,N.证明:.
22.(8分)如图,在中,点E、F在对角线BD上,且.
求证:(1);
(2)四边形AECF是平行四边形.
23.(8分)已知,,求的值.
24.(8分)如图,在中,,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
(1)DE,DF,CG的长之间存在着怎样的数量关系?请加以证明;
(2)若D在底边的延长线上,(1)中的结论还成立吗?若不成立,存在怎样的数量关系?请说明理由.
25.(10分)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,.
(1)求证:四边形OEFG是矩形;
(2)若,求OE和BG的长.
26.(12分)某工厂准备生产A和B两种防疫用品,已知A种防疫用品每箱成本比B种防疫用品每箱成本多500元.经计算,用6000元生产A种防疫用品的箱数与用4500元生产B种防疫用品的箱数相等.请解答下列问题:
(1)求A,B两种防疫用品每箱的成本;
(2)该工厂计划用不超过90000元同时生产A和B两种防疫用品共50箱,且B种防疫用品不超过25箱,该工厂有几种生产方案?
(3)为扩大生产,厂家欲拿出与(2)中最低成本相同的费用全部用于购进甲和乙两种设备(两种都买).若甲种设备每台2500元,乙种设备每台3500元,则有几种购买方案?最多可购买甲,乙两种设备共多少台?(请直接写出答案即可)
答案以及解析
1.答案:C
解析:A.,不能组成三角形,不符合题意;B.,不能组成三角形,不符合题意;C.,,能组成三角形,符合题意;D.,不能组成三角形,不符合题意.故选C.
2.答案:D
解析:由题意,得,解得.故选D.
3.答案:C
解析:∵正多边形的内角和是正多边形的边数为.∵多边形的外角和都是360°,∴该正五边形的每个外角为.
4.答案:C
解析:勾股数需同时满足两个条件:(1)正整数;(2)较小两个数的平方和等于较大数的平方.
5.答案:C
解析:由表格数据可知,成绩为24分、92分的人数为(人),成绩为100分的,出现次数最多,因此成绩的众数是100,成绩从小到大排列后处在第25、26位的两个数都是98分,因此中位数是98,因此中位数和众数与被遮盖的数据无关,故选:C.
6.答案:B
解析:A.添加,利用SAS即可得到两三角形全等,不符合题意;B.添加,不能判定两三角形全等,符合题意;C.添加,利用AAS即可得到两三角形全等,不符合题意;D.添加,可得,利用ASA即可得到两角形全等,不符合题意.故选B.
7.答案:C
解析:四边形ABCD为菱形,
,,
,且点E为CD的中点,
是的中位线,
.
菱形ABCD的周长为:.
故选:C.
8.答案:D
解析:,图像经过第一、二、四象限,A正确;
,y随x的增大而减小,B正确;
当时,,所以图像与y轴的交点为,C正确;
当时,,当时,,D不正确.故选D.
9.答案:C
解析:方程两边同时乘以得,,解得.x为正数,,解得,,,即,m的取值范围是且.故选:C.
10.答案:A
解析:.故选A.
11.答案:D
解析:如图,连接CP,由,,,可得,,,当点E,P,C在同一条直线上时,的最小值为CE的长,此时,由,,,可得,,的最小值等于线段AF的长,故选D.
12.答案:D
解析:,,四边形ABCD是平行四边形,,
.,,.在中,,,,,故选D.
13.答案:3
解析:是正整数,是最简二次根式,,的最小值为3.
14.答案:26°
解析:本题考查平行四边形的性质、三角形的内角和定理、三角形的外角性质.
四边形ABCD是平行四边形,
,.
,
,
,,
,
,
,
.
15.答案:78.8分
解析:因为甲的综合成绩为(分),乙的综合成绩为(分),丙的综合成绩为(分),所以被录取的教师为乙,其综合成绩为78.8分.
16.答案:
解析:如图,连接.
根据勾股定理可以得到,,即是等腰直角三角形,.故答案为.
17.答案:4
解析:,,,,,解得,,.
18.答案:
解析:如图,作D关于x轴y的对称点,连接DB交x轴于E,此时的周长最小. 的周长为.D为CO的中点,.D和关于x轴对称,,易得,设直线的表达式为把,分别代入表达式,得解得表达式为,当时,,故E点坐标为.故答案为.
19.答案:(1)8环.
(2)集训前:8.5;集训后:8.9
(3)由集训前后射击的平均成绩的变化可知,小杰这次集训后的命中环数有所提高.
解析:(2)小杰集训前射击的平均成绩为(环),小杰集训后射击的平均成绩为(环).
20.答案:(1)与全等.
理由:在和中,
,
所以.
(2)因为,
所以,
因为于点E.
所以,是直角三角形,
所以,所以,
所以.
21.答案:证明:如答图,连接BD,取BD的中点H,连接HE,HF.
E,F分别是BC,AD的中点,H是BD的中点,
FH,EH分别是的中位线,
,,
.
,
,
.
22.答案:(1)证明见解析
(2)证明见解析
解析:证明:(1)四边形ABCD为平行四边形,
,,
,
在和中,
,
;
(2)由(1)可知,,
,,
,即,
,
,,
四边形AECF是平行四边形.
23.答案:原式
解析:
.
,,
,,
原式.
24.答案:(1).
证明:如图,连接AD,则,
即,
,.
(2)不成立.理由:①当点D在BC的延长线上时,有.
如图,连接AD,则,
即,
,,
即.
②同理,当点D在CB的延长线上时,有.
25.答案:(1)证明:菱形ABCD的对角线AC,BD相交于点O,
,
E是AD的中点,,
,
四边形OEFG是平行四边形,
,
,
四边形OEFG是矩形.
(2)四边形ABCD是菱形,
.
在中,E为AD的中点,
.
在中,,
.
四边形OEFG是矩形,
,
.
26.答案:(1)A种防疫用品2000元/箱,B种防疫用品1500元/箱
(2)共有6种方案
(3)一共4种方案,最多可购买甲乙两种设备共台
解析:(1)解:设B种防疫用品成本x元/箱,A种防疫用品成本元/箱,
由题意,得,
解得,
检验:当时,,所以是原分式方程的解,
(元/箱),
答:A种防疫用品2000元/箱,B种防疫用品1500元/箱;
(2)解:设B种防疫用品生产m箱,A种防疫用品生产箱,
,解得,
B种防疫用品不超过25箱,
,
m为正整数,
,21,22,23,24,25,共有6种方案;
(3)解:设生产A和B两种防疫用品费用为w,
,
,
w随m的增大而减小,
当时,w取得最小值,此时,
设购进甲和乙两种设备分别为a,b台,
,
,
两种设备都买,
a,b都为正整数,
,,,,
一共4种方案,最多可购买甲乙两种设备共台.
2
【满分:120分】
一、选择题:(本大题共12小题,每小题3分,共36分,给出的四个选项中,只有一项是符合题目要求的)
1.以下列长度的各组线段为边,能组成三角形的是( )
A.2 cm,3 cm,6 cm B.3 cm,4 cm,8 cm
C.5 cm,6 cm,10 cm D.5 cm,6 cm,11 cm
2.二次根式中x的取值范围是( )
A. B. C. D.
3.若正多边形的内角和是540°,则该正多边形的一个外角为( )
A.45° B.60° C.72° D.90°
4.下列四组数中,是勾股数的是( )
A.0.3,0.4,0.5 B.,, C.3,4,5 D.,,
5.为迎接中国共产党建党一百周年,某班50名同学进行了党史知识竞赛,测试成绩统计如下表,其中有两个数据被遮盖.
成绩/分 91 92 93 94 95 96 97 98 99 100
人数 1 2 3 5 6 8 10 12
下列关于成绩的统计量中,与被遮盖的数据无关的是( )
A.平均数,方差 B.中位数,方差 C.中位数,众数 D.平均数,众数
6.如图,在和中,已知,在不添加任何辅助线的前提下,要使,再添加的一个条件不可以是( )
A. B. C. D.
7.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为CD的中点.若,则菱形ABCD的周长为( )
A.6 B.12 C.24 D.48
8.下列关于一次函数的说法,错误的是( )
A.图象经过第一、二、四象限 B.y随x的增大而减小
C.图象与y轴交于点 D.当,时,
9.已知关于x的分式方程的解是正数,则m的取值范围是( )
A. B. C.且 D.且
10.计算的结果是( )
A.5 B.-5 C.7 D.-7
11.如图,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于的最小值的是( )
A.AB B.DE C.BD D.AF
12.如图,平行四边形ABCD的对角线AC与BD相交于点O,,垂足为E,,,,则AE的长为( )
A. B. C. D.
二、填空题:(每小题3分,共18分)
13.若a是正整数,是最简二次根式,则a的最小值为_____________.
14.在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是的对角线,点E在AC上,,,则的大小是________.
15.某校拟招聘一名优秀数学教师,现有甲、乙、丙三名教师入围,三名教师笔试、面试成绩如下表,综合成绩按照笔试占60%,面试占40%进行计算,学校录取综合成绩得分最高者,则被录取的教师的综合成绩为_______.
甲 乙 丙
笔试 80分 82分 78分
面试 76分 74分 78分
16.如图,点分别是正方体(棱长为1)展开图的小正方形的顶点,则的大小为________.
17.若,其中a,b为整数,则的值为_________.
18.如图,在平面直角坐标系中,长方形OABC的顶点O为坐标原点,顶点A,C分别在x轴、y轴上,,,D为OC边的中点,E是OA边上的一个动点,当的周长最小时,E点的坐标为__________.
三、解答题(本大题共8小题,共计66分,解答题应写出演算步骤或证明过程)
19.(6分)为了了解射击运动员小杰的集训效果,教练统计了他集训前后的两次测试成绩(每次测试射击10次),制作了如图的条形统计图.
(1)集训前小杰射击成绩的众数为_______.
(2)分别计算小杰集训前后射击的平均成绩.
(3)请用一句话评价小杰这次集训的效果.
20.(6分)如图,已知,,AC和BD交于点O,于点E.
(1)与全等吗?请说明理由;
(2)若,,求的面积.
21.(8分)如图,在四边形ABCD中,,E,F分别是BC,AD的中点,连接EF并延长,分别与BA,CD的延长线交于点M,N.证明:.
22.(8分)如图,在中,点E、F在对角线BD上,且.
求证:(1);
(2)四边形AECF是平行四边形.
23.(8分)已知,,求的值.
24.(8分)如图,在中,,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
(1)DE,DF,CG的长之间存在着怎样的数量关系?请加以证明;
(2)若D在底边的延长线上,(1)中的结论还成立吗?若不成立,存在怎样的数量关系?请说明理由.
25.(10分)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,.
(1)求证:四边形OEFG是矩形;
(2)若,求OE和BG的长.
26.(12分)某工厂准备生产A和B两种防疫用品,已知A种防疫用品每箱成本比B种防疫用品每箱成本多500元.经计算,用6000元生产A种防疫用品的箱数与用4500元生产B种防疫用品的箱数相等.请解答下列问题:
(1)求A,B两种防疫用品每箱的成本;
(2)该工厂计划用不超过90000元同时生产A和B两种防疫用品共50箱,且B种防疫用品不超过25箱,该工厂有几种生产方案?
(3)为扩大生产,厂家欲拿出与(2)中最低成本相同的费用全部用于购进甲和乙两种设备(两种都买).若甲种设备每台2500元,乙种设备每台3500元,则有几种购买方案?最多可购买甲,乙两种设备共多少台?(请直接写出答案即可)
答案以及解析
1.答案:C
解析:A.,不能组成三角形,不符合题意;B.,不能组成三角形,不符合题意;C.,,能组成三角形,符合题意;D.,不能组成三角形,不符合题意.故选C.
2.答案:D
解析:由题意,得,解得.故选D.
3.答案:C
解析:∵正多边形的内角和是正多边形的边数为.∵多边形的外角和都是360°,∴该正五边形的每个外角为.
4.答案:C
解析:勾股数需同时满足两个条件:(1)正整数;(2)较小两个数的平方和等于较大数的平方.
5.答案:C
解析:由表格数据可知,成绩为24分、92分的人数为(人),成绩为100分的,出现次数最多,因此成绩的众数是100,成绩从小到大排列后处在第25、26位的两个数都是98分,因此中位数是98,因此中位数和众数与被遮盖的数据无关,故选:C.
6.答案:B
解析:A.添加,利用SAS即可得到两三角形全等,不符合题意;B.添加,不能判定两三角形全等,符合题意;C.添加,利用AAS即可得到两三角形全等,不符合题意;D.添加,可得,利用ASA即可得到两角形全等,不符合题意.故选B.
7.答案:C
解析:四边形ABCD为菱形,
,,
,且点E为CD的中点,
是的中位线,
.
菱形ABCD的周长为:.
故选:C.
8.答案:D
解析:,图像经过第一、二、四象限,A正确;
,y随x的增大而减小,B正确;
当时,,所以图像与y轴的交点为,C正确;
当时,,当时,,D不正确.故选D.
9.答案:C
解析:方程两边同时乘以得,,解得.x为正数,,解得,,,即,m的取值范围是且.故选:C.
10.答案:A
解析:.故选A.
11.答案:D
解析:如图,连接CP,由,,,可得,,,当点E,P,C在同一条直线上时,的最小值为CE的长,此时,由,,,可得,,的最小值等于线段AF的长,故选D.
12.答案:D
解析:,,四边形ABCD是平行四边形,,
.,,.在中,,,,,故选D.
13.答案:3
解析:是正整数,是最简二次根式,,的最小值为3.
14.答案:26°
解析:本题考查平行四边形的性质、三角形的内角和定理、三角形的外角性质.
四边形ABCD是平行四边形,
,.
,
,
,,
,
,
,
.
15.答案:78.8分
解析:因为甲的综合成绩为(分),乙的综合成绩为(分),丙的综合成绩为(分),所以被录取的教师为乙,其综合成绩为78.8分.
16.答案:
解析:如图,连接.
根据勾股定理可以得到,,即是等腰直角三角形,.故答案为.
17.答案:4
解析:,,,,,解得,,.
18.答案:
解析:如图,作D关于x轴y的对称点,连接DB交x轴于E,此时的周长最小. 的周长为.D为CO的中点,.D和关于x轴对称,,易得,设直线的表达式为把,分别代入表达式,得解得表达式为,当时,,故E点坐标为.故答案为.
19.答案:(1)8环.
(2)集训前:8.5;集训后:8.9
(3)由集训前后射击的平均成绩的变化可知,小杰这次集训后的命中环数有所提高.
解析:(2)小杰集训前射击的平均成绩为(环),小杰集训后射击的平均成绩为(环).
20.答案:(1)与全等.
理由:在和中,
,
所以.
(2)因为,
所以,
因为于点E.
所以,是直角三角形,
所以,所以,
所以.
21.答案:证明:如答图,连接BD,取BD的中点H,连接HE,HF.
E,F分别是BC,AD的中点,H是BD的中点,
FH,EH分别是的中位线,
,,
.
,
,
.
22.答案:(1)证明见解析
(2)证明见解析
解析:证明:(1)四边形ABCD为平行四边形,
,,
,
在和中,
,
;
(2)由(1)可知,,
,,
,即,
,
,,
四边形AECF是平行四边形.
23.答案:原式
解析:
.
,,
,,
原式.
24.答案:(1).
证明:如图,连接AD,则,
即,
,.
(2)不成立.理由:①当点D在BC的延长线上时,有.
如图,连接AD,则,
即,
,,
即.
②同理,当点D在CB的延长线上时,有.
25.答案:(1)证明:菱形ABCD的对角线AC,BD相交于点O,
,
E是AD的中点,,
,
四边形OEFG是平行四边形,
,
,
四边形OEFG是矩形.
(2)四边形ABCD是菱形,
.
在中,E为AD的中点,
.
在中,,
.
四边形OEFG是矩形,
,
.
26.答案:(1)A种防疫用品2000元/箱,B种防疫用品1500元/箱
(2)共有6种方案
(3)一共4种方案,最多可购买甲乙两种设备共台
解析:(1)解:设B种防疫用品成本x元/箱,A种防疫用品成本元/箱,
由题意,得,
解得,
检验:当时,,所以是原分式方程的解,
(元/箱),
答:A种防疫用品2000元/箱,B种防疫用品1500元/箱;
(2)解:设B种防疫用品生产m箱,A种防疫用品生产箱,
,解得,
B种防疫用品不超过25箱,
,
m为正整数,
,21,22,23,24,25,共有6种方案;
(3)解:设生产A和B两种防疫用品费用为w,
,
,
w随m的增大而减小,
当时,w取得最小值,此时,
设购进甲和乙两种设备分别为a,b台,
,
,
两种设备都买,
a,b都为正整数,
,,,,
一共4种方案,最多可购买甲乙两种设备共台.
2
同课章节目录
