2022-2023学年人教版九年级上学期开学摸底考试数学试卷B卷(word版 含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级上学期开学摸底考试数学试卷B卷(word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 745.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览




文档简介
九年级上学期开学摸底考试数学试卷B卷(模拟试卷)
【满分:120分】
一、选择题:(本大题共12小题,每小题3分,共36分,给出的四个选项中,只有一项是符合题目要求的)
1.冬季奥林匹克运动会是世界上规模最大的冬季综合性运动会,下列四个图是历届冬奥会图标中的一部分,其中是轴对称图形的为( )
A. B. C. D.
2.计算的结果为( )
A.-1 B.1 C. D.
3.如图,,,,则的度数为( )
A.45° B.48° C.50° D.58°
4.小明同学连续5次测验的成绩分别为:97,97,99,101,106(单位:分),则这组数据的众数和平均数分别为( )
A.97和99 B.97和100 C.99和100 D.97和101
5.小明和小强两人在公路上匀速骑行,小强骑行28km所用时间与小明骑行24km所用时间相等,已知小强每小时比小明多骑行2km,小强每小时骑行多少千米?设小强每小时骑行x km,所列方程正确的是( )
A. B. C. D.
6.已知两地相距3 km,小黄从A地到B地,平均速度为4 km/h,若用表示行走的时间,表示余下的路程,则y关于x的函数解析式是( )
A. B.
C. D.
7.计算的值为( )
A.2 B.3 C.4 D.1
8.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的处.若,则等于( )
A.66° B.60° C.57° D.48°
9.在四边形ABCD中,,,,,分别以A,C为圆心,大于的长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O,若点O是AC的中点,则CD的长为( )
A. B. C.6 D.8
10.如图,在正方形的外侧,作等边三角形,则的度数为( )
A.15° B.35° C.45° D.55°
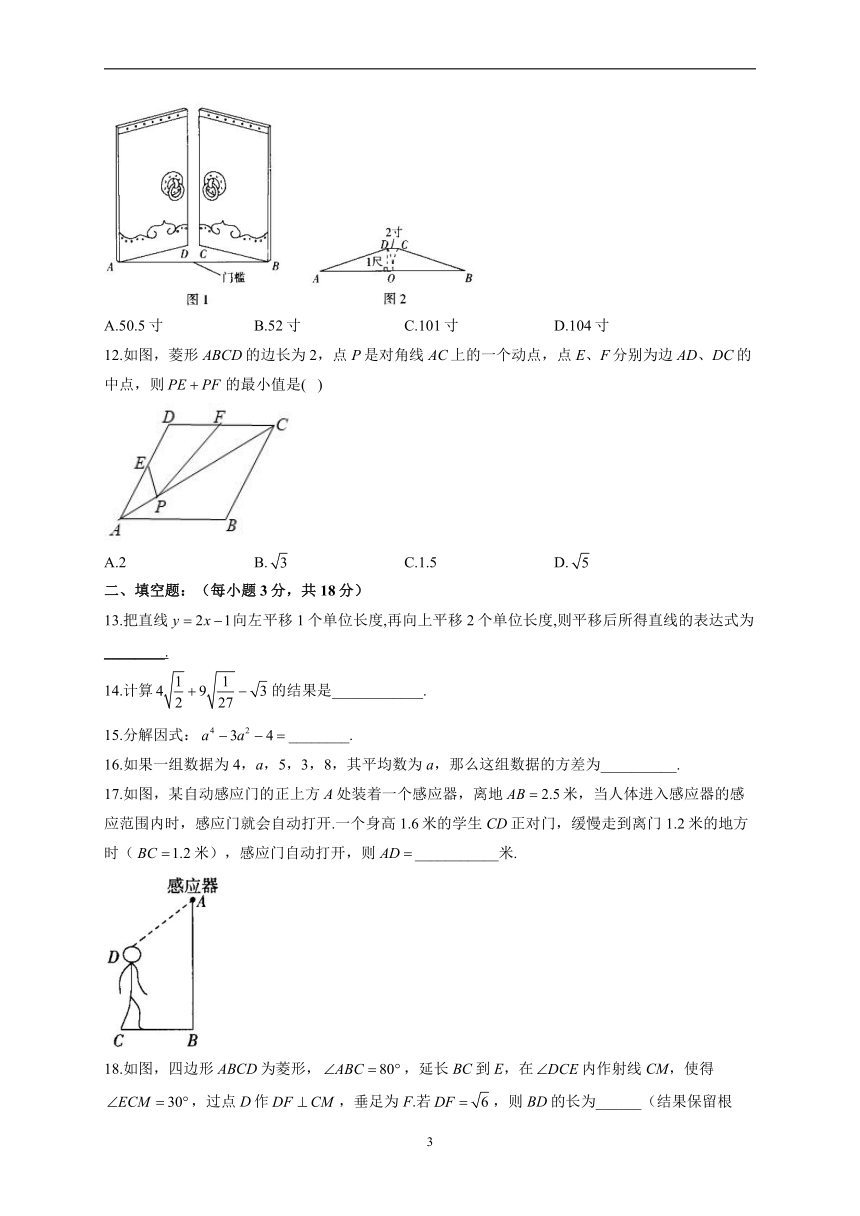
11.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺寸),则AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
12.如图,菱形ABCD的边长为2,点P是对角线AC上的一个动点,点E、F分别为边AD、DC的中点,则的最小值是( )
A.2 B. C.1.5 D.
二、填空题:(每小题3分,共18分)
13.把直线向左平移1个单位长度,再向上平移2个单位长度,则平移后所得直线的表达式为________.
14.计算的结果是____________.
15.分解因式:________.
16.如果一组数据为4,a,5,3,8,其平均数为a,那么这组数据的方差为__________.
17.如图,某自动感应门的正上方A处装着一个感应器,离地米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(米),感应门自动打开,则___________米.
18.如图,四边形ABCD为菱形,,延长BC到E,在内作射线CM,使得,过点D作,垂足为F.若,则BD的长为______(结果保留根号).
三、解答题(本大题共8小题,共计66分,解答题应写出演算步骤或证明过程)
19.(6分)如图,某工厂C前面有一条笔直的公路,原来有两条路AC,BC可以从工厂C到达公路,经测量m,m,m,现需要修建一条路,使工厂C到公路的路程最短,请你帮工厂C的负责人设计一种方案,并求出新建的路的长.
20.(6分)如图,在中,对角线与相交于点O,点分别在和的延长线上,且,连接.求证:.
21.(8分)先化简,再求值:,其中.
22.(8分)如图,在中,E为的中点,连接并延长交的延长线于点F,连接.若,求证:四边形是矩形.
23.(8分)如图,直线与x轴、y轴分别相交于点AB,设M是OB上一点,若将沿AM折叠,使点B恰好落在x轴上的点 处.求:
(1)点的坐标.
(2)直线AM所对应的函数表达式.
24.(8分)甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环 中位数/环 众数/环 方差
甲 a 7 7 12
乙 7 b 8 c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
25.(10分)探究:如图,分别以的两边AB和AC为边向外作正方形ANMB和正方形ACDE交于点P.
(1)求证:
(2)应用:Q是线段BC的中点,若则__________.
26.(12分)如图所示,、均是等边三角形,点A、C、B在同一条直线上,AE交CD于点M,BD交CE于点N,连接MN.
(1)试证明;
(2)试证明;
(3)是什么三角形?请说明理由.
答案以及解析
1.答案:A
解析:选项B、C、D不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
选项A能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
故选:A.
2.答案:B
解析:.故选B.
3.答案:B
解析:如图,,,又,,故选B.
4.答案:B
解析:解:小明同学连续5次测验的成绩分别为:97,97,99,101,106(单位:分),
这组成绩的众数是97;平均数是,故选:B.
5.答案:D
解析:小强每小时比小明多骑行2km,小强每小时骑行x km,小明每小时骑行km.依题意得:.故选:D.
6.答案:D
解析:由题意,得走完全程需要的时间为.
7.答案:D
解析:.故选D.
8.答案:C
解析:本题考查了全等三角形的性质.由题意得,,,.四边形ABCD是矩形,,又,,.故选C.
9.答案:A
解析:如图,连接FC,
由题可得,点E和点O在AC的垂直平分线上,
垂直平分AC,
,
,
,
在与中,
,
,
,
,.
在中,,
,
即,
解得.
故选A.
10.答案:C
解析:在正方形中,.在等边三角形中.在中,,,.
11.答案:C
解析:由题知AB的中点为O,过D作于E,如图所示.
由题意得,寸,寸,
设寸,则寸,寸,
在中,,
即,
解得,
,寸,故选C.
12.答案:A
解析:如图,取AB是中点T,连接PT,FT.
四边形ABCD是菱形,
,,
,,
,,
四边形ADFT是平行四边形,
,
四边形ABCD是菱形,,,
E,T关于AC对称,
,
,
,
,
的最小值为2.
故选:A.
13.答案:
解析:把直线向左平移1个单位长度,得到,
再向上平移2个单位长度,得到.
故答案为:.
14.答案:
解析:.
15.答案:
解析:解:
,
故答案为:.
16.答案:2.8
解析:因为这组数据4,a,5,3,8的平均数为a,所以,解得,故这组数据的方差.
17.答案:1.5
解析:如图所示,过点D作于点E,
米,米,米,则(米).在中,由勾股定理得,(米).
18.答案:
解析:解:如图,连接AC交BD于点H,
由菱形的性质得,,,又,,,,,又四边形ABCD是菱形,BD平分,,在和中,,,,.故答案为:.
19.答案:过点C作公路AB的垂线,垂足为D,则线段CD即为新建的路.
,,
,为直角三角形.
由三角形的面积公式知,
,
m,即新建的路的长为480m.
20.答案:见解析
解析:证明:∵四边形是平行四边形,
.
又,
.
在和中,
.
21.答案:原式
解析:
,
当时,原式.
22.答案:见解析
解析:证明:四边形是平行四边形,
.
为的中点,.
又.
又四边形是平行四边形.
四边形是矩形.
23.答案:(1)在,令,则.
令,,,,,.
在中,由勾股定理,得,
,.
在x轴的负半轴上,.
(2)令,则.又,由勾股定理,得,解得,.由(1)知,设直线AM所对应的函数表达式为,则,解得,直线AM所对应的函数表达式为.
24.答案:(1)甲的平均成绩(环).
乙射击的成绩从小到大重新排列为3,4,6,7,7,8,8,8,9,10,
乙射击成绩的中位数(环),
其方差
.
(2)从平均成绩看甲、乙两人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定.综合以上各因素,若选派一名队员参加比赛的话,可选择乙参赛,因为乙获得高分的可能性更大.
25.答案:(1)四边形ANMB和ACDE是正方形,,.
,,
.
在和中,
,
.
(2)设AB与NC相交于点O.四边形NABM是正方形,
.,,
,,
Q为BC中点,,.
26.答案:(1)证明:、均是等边三角形,
,,,
,即.
在和中,,,,
,.
(2)证明:由(1)知,,即.
点A、C、B在同一条直线上,
,
即,.
在和中,,,,
,.
(3)是等边三角形.
理由:由(2)知,,
是等边三角形.
2
【满分:120分】
一、选择题:(本大题共12小题,每小题3分,共36分,给出的四个选项中,只有一项是符合题目要求的)
1.冬季奥林匹克运动会是世界上规模最大的冬季综合性运动会,下列四个图是历届冬奥会图标中的一部分,其中是轴对称图形的为( )
A. B. C. D.
2.计算的结果为( )
A.-1 B.1 C. D.
3.如图,,,,则的度数为( )
A.45° B.48° C.50° D.58°
4.小明同学连续5次测验的成绩分别为:97,97,99,101,106(单位:分),则这组数据的众数和平均数分别为( )
A.97和99 B.97和100 C.99和100 D.97和101
5.小明和小强两人在公路上匀速骑行,小强骑行28km所用时间与小明骑行24km所用时间相等,已知小强每小时比小明多骑行2km,小强每小时骑行多少千米?设小强每小时骑行x km,所列方程正确的是( )
A. B. C. D.
6.已知两地相距3 km,小黄从A地到B地,平均速度为4 km/h,若用表示行走的时间,表示余下的路程,则y关于x的函数解析式是( )
A. B.
C. D.
7.计算的值为( )
A.2 B.3 C.4 D.1
8.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的处.若,则等于( )
A.66° B.60° C.57° D.48°
9.在四边形ABCD中,,,,,分别以A,C为圆心,大于的长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O,若点O是AC的中点,则CD的长为( )
A. B. C.6 D.8
10.如图,在正方形的外侧,作等边三角形,则的度数为( )
A.15° B.35° C.45° D.55°
11.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺寸),则AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
12.如图,菱形ABCD的边长为2,点P是对角线AC上的一个动点,点E、F分别为边AD、DC的中点,则的最小值是( )
A.2 B. C.1.5 D.
二、填空题:(每小题3分,共18分)
13.把直线向左平移1个单位长度,再向上平移2个单位长度,则平移后所得直线的表达式为________.
14.计算的结果是____________.
15.分解因式:________.
16.如果一组数据为4,a,5,3,8,其平均数为a,那么这组数据的方差为__________.
17.如图,某自动感应门的正上方A处装着一个感应器,离地米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(米),感应门自动打开,则___________米.
18.如图,四边形ABCD为菱形,,延长BC到E,在内作射线CM,使得,过点D作,垂足为F.若,则BD的长为______(结果保留根号).
三、解答题(本大题共8小题,共计66分,解答题应写出演算步骤或证明过程)
19.(6分)如图,某工厂C前面有一条笔直的公路,原来有两条路AC,BC可以从工厂C到达公路,经测量m,m,m,现需要修建一条路,使工厂C到公路的路程最短,请你帮工厂C的负责人设计一种方案,并求出新建的路的长.
20.(6分)如图,在中,对角线与相交于点O,点分别在和的延长线上,且,连接.求证:.
21.(8分)先化简,再求值:,其中.
22.(8分)如图,在中,E为的中点,连接并延长交的延长线于点F,连接.若,求证:四边形是矩形.
23.(8分)如图,直线与x轴、y轴分别相交于点AB,设M是OB上一点,若将沿AM折叠,使点B恰好落在x轴上的点 处.求:
(1)点的坐标.
(2)直线AM所对应的函数表达式.
24.(8分)甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环 中位数/环 众数/环 方差
甲 a 7 7 12
乙 7 b 8 c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
25.(10分)探究:如图,分别以的两边AB和AC为边向外作正方形ANMB和正方形ACDE交于点P.
(1)求证:
(2)应用:Q是线段BC的中点,若则__________.
26.(12分)如图所示,、均是等边三角形,点A、C、B在同一条直线上,AE交CD于点M,BD交CE于点N,连接MN.
(1)试证明;
(2)试证明;
(3)是什么三角形?请说明理由.
答案以及解析
1.答案:A
解析:选项B、C、D不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
选项A能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
故选:A.
2.答案:B
解析:.故选B.
3.答案:B
解析:如图,,,又,,故选B.
4.答案:B
解析:解:小明同学连续5次测验的成绩分别为:97,97,99,101,106(单位:分),
这组成绩的众数是97;平均数是,故选:B.
5.答案:D
解析:小强每小时比小明多骑行2km,小强每小时骑行x km,小明每小时骑行km.依题意得:.故选:D.
6.答案:D
解析:由题意,得走完全程需要的时间为.
7.答案:D
解析:.故选D.
8.答案:C
解析:本题考查了全等三角形的性质.由题意得,,,.四边形ABCD是矩形,,又,,.故选C.
9.答案:A
解析:如图,连接FC,
由题可得,点E和点O在AC的垂直平分线上,
垂直平分AC,
,
,
,
在与中,
,
,
,
,.
在中,,
,
即,
解得.
故选A.
10.答案:C
解析:在正方形中,.在等边三角形中.在中,,,.
11.答案:C
解析:由题知AB的中点为O,过D作于E,如图所示.
由题意得,寸,寸,
设寸,则寸,寸,
在中,,
即,
解得,
,寸,故选C.
12.答案:A
解析:如图,取AB是中点T,连接PT,FT.
四边形ABCD是菱形,
,,
,,
,,
四边形ADFT是平行四边形,
,
四边形ABCD是菱形,,,
E,T关于AC对称,
,
,
,
,
的最小值为2.
故选:A.
13.答案:
解析:把直线向左平移1个单位长度,得到,
再向上平移2个单位长度,得到.
故答案为:.
14.答案:
解析:.
15.答案:
解析:解:
,
故答案为:.
16.答案:2.8
解析:因为这组数据4,a,5,3,8的平均数为a,所以,解得,故这组数据的方差.
17.答案:1.5
解析:如图所示,过点D作于点E,
米,米,米,则(米).在中,由勾股定理得,(米).
18.答案:
解析:解:如图,连接AC交BD于点H,
由菱形的性质得,,,又,,,,,又四边形ABCD是菱形,BD平分,,在和中,,,,.故答案为:.
19.答案:过点C作公路AB的垂线,垂足为D,则线段CD即为新建的路.
,,
,为直角三角形.
由三角形的面积公式知,
,
m,即新建的路的长为480m.
20.答案:见解析
解析:证明:∵四边形是平行四边形,
.
又,
.
在和中,
.
21.答案:原式
解析:
,
当时,原式.
22.答案:见解析
解析:证明:四边形是平行四边形,
.
为的中点,.
又.
又四边形是平行四边形.
四边形是矩形.
23.答案:(1)在,令,则.
令,,,,,.
在中,由勾股定理,得,
,.
在x轴的负半轴上,.
(2)令,则.又,由勾股定理,得,解得,.由(1)知,设直线AM所对应的函数表达式为,则,解得,直线AM所对应的函数表达式为.
24.答案:(1)甲的平均成绩(环).
乙射击的成绩从小到大重新排列为3,4,6,7,7,8,8,8,9,10,
乙射击成绩的中位数(环),
其方差
.
(2)从平均成绩看甲、乙两人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定.综合以上各因素,若选派一名队员参加比赛的话,可选择乙参赛,因为乙获得高分的可能性更大.
25.答案:(1)四边形ANMB和ACDE是正方形,,.
,,
.
在和中,
,
.
(2)设AB与NC相交于点O.四边形NABM是正方形,
.,,
,,
Q为BC中点,,.
26.答案:(1)证明:、均是等边三角形,
,,,
,即.
在和中,,,,
,.
(2)证明:由(1)知,,即.
点A、C、B在同一条直线上,
,
即,.
在和中,,,,
,.
(3)是等边三角形.
理由:由(2)知,,
是等边三角形.
2
同课章节目录
