2022-2023学年北师大版八年级上学期开学摸底考试数学试卷A卷(word版 含解析)
文档属性
| 名称 | 2022-2023学年北师大版八年级上学期开学摸底考试数学试卷A卷(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 744.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 19:58:14 | ||
图片预览

文档简介
八年级上学期开学考试数学试卷A卷(模拟试卷)
一、选择题:(本大题共12小题,每小题3分,共36分,给出的四个选项中,只有一项是符合题目要求的)
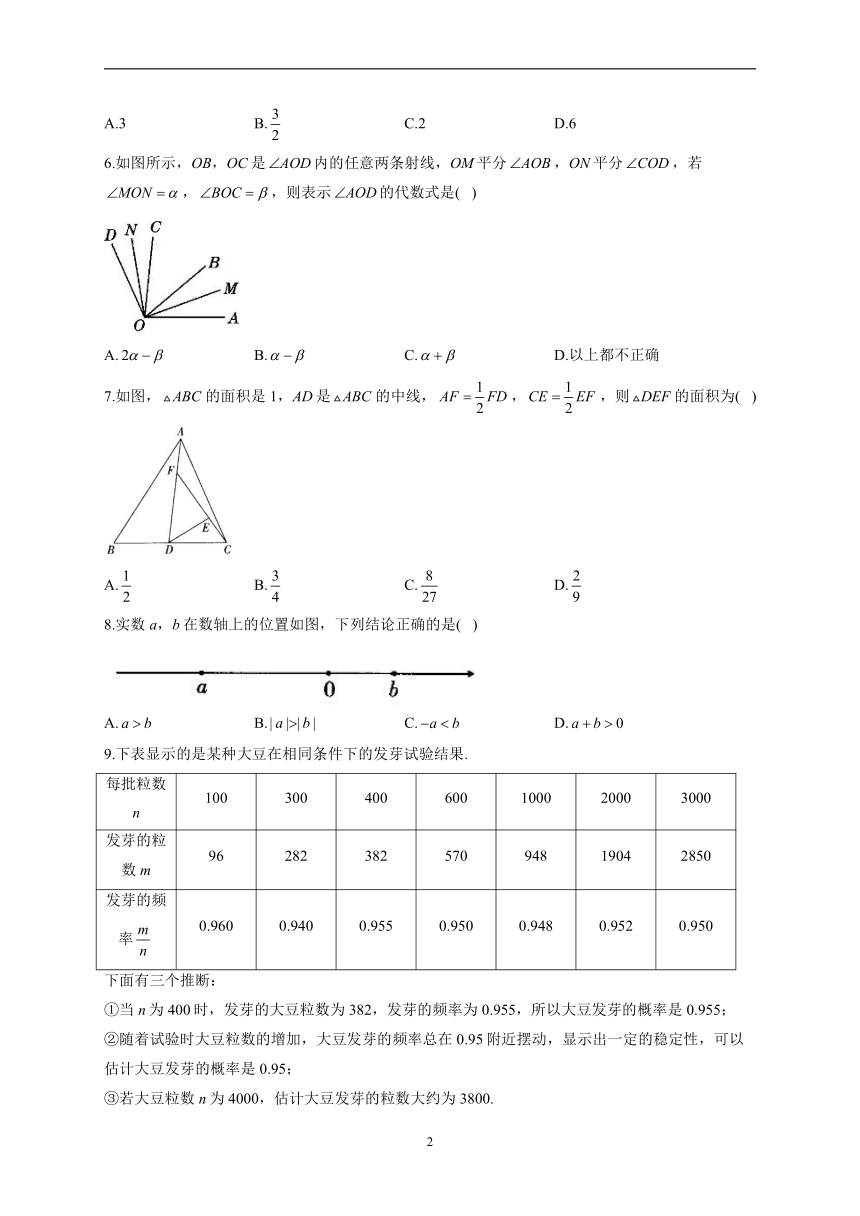
1.如图是某几何体的展开图,该几何体是( )
A.长方体 B.圆柱 C.圆锥 D.三棱柱
2.如图,下列条件能判定直线的是( )
A. B. C. D.
3.下列变量之间的关系不是函数关系的是( )
A.一天的气温和时间
B.中的y与x
C.银行中的利息与时间
D.正方形的周长与面积
4.下列运算一定正确的是( )
A. B. C. D.
5.在中,,AD平分,交BC于点D,,垂足为点E,若,则DE的长为( )
A.3 B. C.2 D.6
6.如图所示,OB,OC是内的任意两条射线,OM平分,ON平分,若,,则表示的代数式是( )
A. B. C. D.以上都不正确
7.如图,的面积是1,AD是的中线,,,则的面积为( )
A. B. C. D.
8.实数a,b在数轴上的位置如图,下列结论正确的是( )
A. B. C. D.
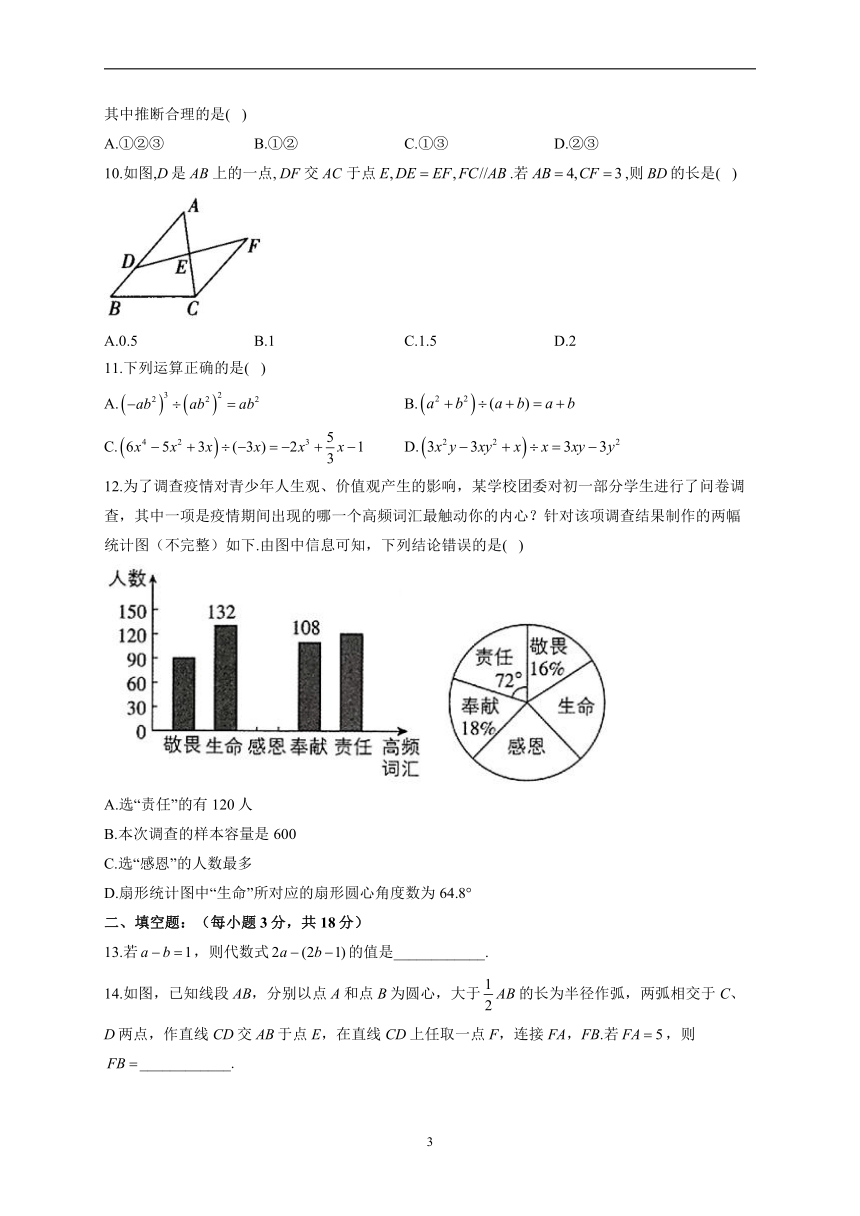
9.下表显示的是某种大豆在相同条件下的发芽试验结果.
每批粒数n 100 300 400 600 1000 2000 3000
发芽的粒数m 96 282 382 570 948 1904 2850
发芽的频率 0.960 0.940 0.955 0.950 0.948 0.952 0.950
下面有三个推断:
①当n为400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率是0.955;
②随着试验时大豆粒数的增加,大豆发芽的频率总在0.95附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是0.95;
③若大豆粒数n为4000,估计大豆发芽的粒数大约为3800.
其中推断合理的是( )
A.①②③ B.①② C.①③ D.②③
10.如图,D是上的一点,交于点.若,则的长是( )
A.0.5 B.1 C.1.5 D.2
11.下列运算正确的是( )
A. B.
C. D.
12.为了调查疫情对青少年人生观、价值观产生的影响,某学校团委对初一部分学生进行了问卷调查,其中一项是疫情期间出现的哪一个高频词汇最触动你的内心?针对该项调查结果制作的两幅统计图(不完整)如下.由图中信息可知,下列结论错误的是( )
A.选“责任”的有120人
B.本次调查的样本容量是600
C.选“感恩”的人数最多
D.扇形统计图中“生命”所对应的扇形圆心角度数为64.8°
二、填空题:(每小题3分,共18分)
13.若,则代数式的值是____________.
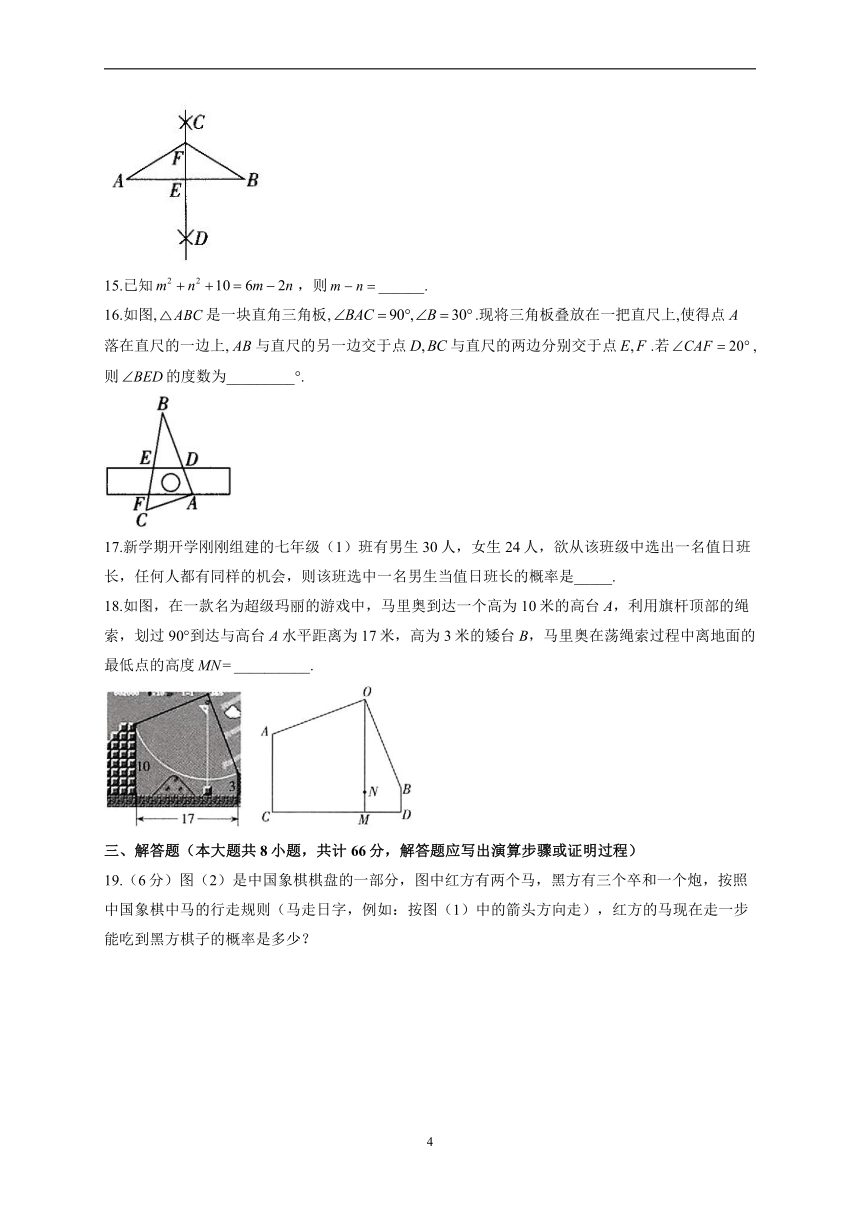
14.如图,已知线段AB,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于C、D两点,作直线CD交AB于点E,在直线CD上任取一点F,连接FA,FB.若,则____________.
15.已知,则______.
16.如图,是一块直角三角板,.现将三角板叠放在一把直尺上,使得点A落在直尺的一边上,与直尺的另一边交于点与直尺的两边分别交于点.若,则的度数为_________°.
17.新学期开学刚刚组建的七年级(1)班有男生30人,女生24人,欲从该班级中选出一名值日班长,任何人都有同样的机会,则该班选中一名男生当值日班长的概率是_____.
18.如图,在一款名为超级玛丽的游戏中,马里奥到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,马里奥在荡绳索过程中离地面的最低点的高度__________.
三、解答题(本大题共8小题,共计66分,解答题应写出演算步骤或证明过程)
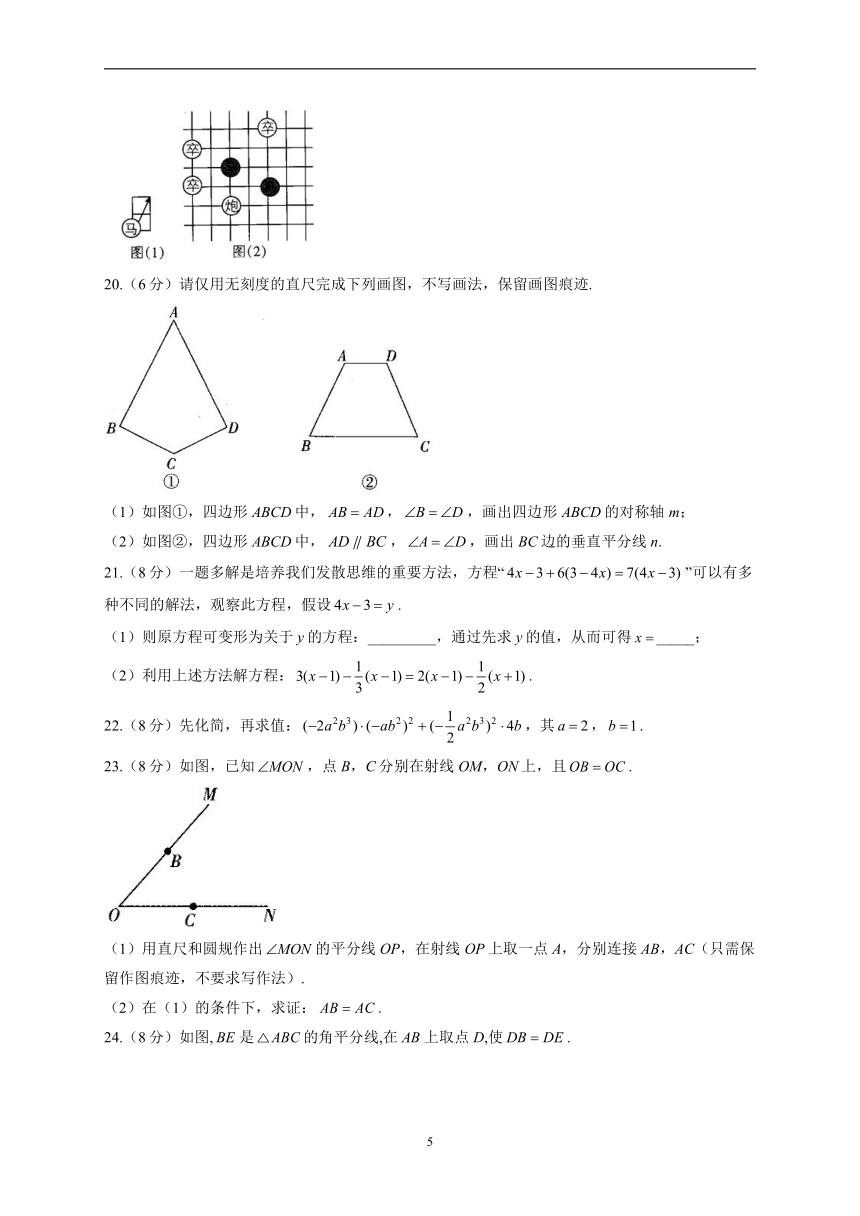
19.(6分)图(2)是中国象棋棋盘的一部分,图中红方有两个马,黑方有三个卒和一个炮,按照中国象棋中马的行走规则(马走日字,例如:按图(1)中的箭头方向走),红方的马现在走一步能吃到黑方棋子的概率是多少?
20.(6分)请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图①,四边形ABCD中,,,画出四边形ABCD的对称轴m;
(2)如图②,四边形ABCD中,,,画出BC边的垂直平分线n.
21.(8分)一题多解是培养我们发散思维的重要方法,方程“”可以有多种不同的解法,观察此方程,假设.
(1)则原方程可变形为关于y的方程:_________,通过先求y的值,从而可得_____;
(2)利用上述方法解方程:.
22.(8分)先化简,再求值:,其,.
23.(8分)如图,已知,点B,C分别在射线OM,ON上,且.
(1)用直尺和圆规作出的平分线OP,在射线OP上取一点A,分别连接AB,AC(只需保留作图痕迹,不要求写作法).
(2)在(1)的条件下,求证:.
24.(8分)如图,是的角平分线,在上取点D,使.
(1)求证:.
(2)若,求的度数.
25.(10分)如图,一条河流MN旁边有两个村庄A,B,于D.由于有山峰阻挡,村庄B到河边MN的距离不能直接测量,河边恰好有一个地点C能到达A,B两个村庄,且为90°,C与A,B的距离相等,测量C,D的距离为150m,请求出村庄B到河边的距离.
26.(12分)如图,画,并画的平分线OC.
(1)将三角尺的直角顶点落在OC的任意一点P处,使三角尺的两条直角边与的两边分别垂直,垂足分别为E、F(如图①),则PE____________PF;(填“>”“<”或“=”)
(2)把三角尺绕着点P旋转(如图②),两直角边分别与OA、OB交于点E、F,那么PE与PF相等吗?试猜想PE与PF的大小关系,并说明理由.
答案以及解析
1.答案:B
解析:由图形可得该几何体是圆柱;故选B.
2.答案:C
解析:与是直线被所截而成的同旁内角,当时,.
3.答案:B
解析:A选项,一天的气温和时间的关系是函数关系,
故本选项不合题意;
B选项,中的y与x的关系不是函数关系,故本选项符合题意;
C选项,在银行中利息与时间是函数关系,故本选项不合题意;
D选项,正方形的周长与面积是函数关系,故本选项不合题意.故选B.
4.答案:C
解析:
选项 分析 正误
A ×
B ×
C √
D ×
5.答案:A
解析:,.又AD平分,,,故选A.
6.答案:A
解析:,,
.
又OM平分,ON平分,
,.
.
7.答案:D
解析:的面积是1,AD是的中线,,,,,,,故选D.
8.答案:B
解析:由数轴可知,.
9.答案:D
解析:①当时,发芽的大豆粒数为382,发芽的频率为0.955,根据一次的试验频率不能估计大豆发芽的概率是0.955,故此推断错误;
②根据题表,当每批粒数足够大时,频率逐渐接近于0.950,所以估计大豆发芽的概率是0.95,此推断正确;
③若n为4000,估计大豆发芽的粒数大约为,此结论正确.故选D.
10.答案:B
解析:.在和中,
,.
11.答案:C
解析:A项,;B项应为;D项, .故选C.
12.答案:D
解析:选“责任”的有(人),故选项A正确;根据条形统计图与扇形统计图中选“奉献”的数据知调查的样本容量是,故选项B正确;选“生命”的占比,选“责任”的占比,则选“感恩”的人占比为,故选“感恩”的人数最多,故选项C正确;,故选项D错误,故选D.
13.答案:3
解析:原式,,原式.
14.答案:5
解析:由题意知直线CD是线段AB的垂直平分线,点F在直线CD上,,,.故答案为5.
15.答案:4
解析:,,即,,,,故答案为:4.
16.答案:80
解析:.
17.答案:
解析:全班共有学生(人),其中男生30人,
则该班选中一名男生当值日班长的概率是.故答案为.
18.答案:2米
解析:如图,作,,,,在和中,,,,,即(m),m.(m),m,m,m,易知m,又m,(m).马里奥在荡绳索过程中离地面的最低点的高度MN为2米.
19.答案:红方的马走一步可能的走法有14种等可能的结果,
其中有3种情况吃到了黑方棋子,
则红方的马现在走一步能吃到黑方棋子的概率是.
20.答案:(1)如图①,直线m即为所求.
(2)如图②,直线n即为所求.
21.答案:(1)则原方程可变形为关于y的方程:,解得,所以,所以.故答案为,.
(2),
移项、合并同类项,得.
令,所以,去括号,得.
移项,得.合并同类项,得.
系数化为1,得.所以.
22.答案:原式
.
当,时,原式.
23.答案:(1)见解析
(2)见解析
解析:(1)如图所示:
(2)由(1)知,OP是的平分线,
.
在与中,
,
.
24.答案:(1)见解析
(2)35°
解析:(1)证明:平分.
,
.
(2),
.
.
平分.
25.答案:如图,过点B作于点E,
,
,,
.
在与中,
,
.
m,
即村庄B到河边的距离是150m.
26.答案:(1)=.
(2).理由:如图,过点P作,,垂足分别为M,N,
则,
OP平分,,
,
,
,.
在和中,,
,.
2
一、选择题:(本大题共12小题,每小题3分,共36分,给出的四个选项中,只有一项是符合题目要求的)
1.如图是某几何体的展开图,该几何体是( )
A.长方体 B.圆柱 C.圆锥 D.三棱柱
2.如图,下列条件能判定直线的是( )
A. B. C. D.
3.下列变量之间的关系不是函数关系的是( )
A.一天的气温和时间
B.中的y与x
C.银行中的利息与时间
D.正方形的周长与面积
4.下列运算一定正确的是( )
A. B. C. D.
5.在中,,AD平分,交BC于点D,,垂足为点E,若,则DE的长为( )
A.3 B. C.2 D.6
6.如图所示,OB,OC是内的任意两条射线,OM平分,ON平分,若,,则表示的代数式是( )
A. B. C. D.以上都不正确
7.如图,的面积是1,AD是的中线,,,则的面积为( )
A. B. C. D.
8.实数a,b在数轴上的位置如图,下列结论正确的是( )
A. B. C. D.
9.下表显示的是某种大豆在相同条件下的发芽试验结果.
每批粒数n 100 300 400 600 1000 2000 3000
发芽的粒数m 96 282 382 570 948 1904 2850
发芽的频率 0.960 0.940 0.955 0.950 0.948 0.952 0.950
下面有三个推断:
①当n为400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率是0.955;
②随着试验时大豆粒数的增加,大豆发芽的频率总在0.95附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是0.95;
③若大豆粒数n为4000,估计大豆发芽的粒数大约为3800.
其中推断合理的是( )
A.①②③ B.①② C.①③ D.②③
10.如图,D是上的一点,交于点.若,则的长是( )
A.0.5 B.1 C.1.5 D.2
11.下列运算正确的是( )
A. B.
C. D.
12.为了调查疫情对青少年人生观、价值观产生的影响,某学校团委对初一部分学生进行了问卷调查,其中一项是疫情期间出现的哪一个高频词汇最触动你的内心?针对该项调查结果制作的两幅统计图(不完整)如下.由图中信息可知,下列结论错误的是( )
A.选“责任”的有120人
B.本次调查的样本容量是600
C.选“感恩”的人数最多
D.扇形统计图中“生命”所对应的扇形圆心角度数为64.8°
二、填空题:(每小题3分,共18分)
13.若,则代数式的值是____________.
14.如图,已知线段AB,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于C、D两点,作直线CD交AB于点E,在直线CD上任取一点F,连接FA,FB.若,则____________.
15.已知,则______.
16.如图,是一块直角三角板,.现将三角板叠放在一把直尺上,使得点A落在直尺的一边上,与直尺的另一边交于点与直尺的两边分别交于点.若,则的度数为_________°.
17.新学期开学刚刚组建的七年级(1)班有男生30人,女生24人,欲从该班级中选出一名值日班长,任何人都有同样的机会,则该班选中一名男生当值日班长的概率是_____.
18.如图,在一款名为超级玛丽的游戏中,马里奥到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,马里奥在荡绳索过程中离地面的最低点的高度__________.
三、解答题(本大题共8小题,共计66分,解答题应写出演算步骤或证明过程)
19.(6分)图(2)是中国象棋棋盘的一部分,图中红方有两个马,黑方有三个卒和一个炮,按照中国象棋中马的行走规则(马走日字,例如:按图(1)中的箭头方向走),红方的马现在走一步能吃到黑方棋子的概率是多少?
20.(6分)请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图①,四边形ABCD中,,,画出四边形ABCD的对称轴m;
(2)如图②,四边形ABCD中,,,画出BC边的垂直平分线n.
21.(8分)一题多解是培养我们发散思维的重要方法,方程“”可以有多种不同的解法,观察此方程,假设.
(1)则原方程可变形为关于y的方程:_________,通过先求y的值,从而可得_____;
(2)利用上述方法解方程:.
22.(8分)先化简,再求值:,其,.
23.(8分)如图,已知,点B,C分别在射线OM,ON上,且.
(1)用直尺和圆规作出的平分线OP,在射线OP上取一点A,分别连接AB,AC(只需保留作图痕迹,不要求写作法).
(2)在(1)的条件下,求证:.
24.(8分)如图,是的角平分线,在上取点D,使.
(1)求证:.
(2)若,求的度数.
25.(10分)如图,一条河流MN旁边有两个村庄A,B,于D.由于有山峰阻挡,村庄B到河边MN的距离不能直接测量,河边恰好有一个地点C能到达A,B两个村庄,且为90°,C与A,B的距离相等,测量C,D的距离为150m,请求出村庄B到河边的距离.
26.(12分)如图,画,并画的平分线OC.
(1)将三角尺的直角顶点落在OC的任意一点P处,使三角尺的两条直角边与的两边分别垂直,垂足分别为E、F(如图①),则PE____________PF;(填“>”“<”或“=”)
(2)把三角尺绕着点P旋转(如图②),两直角边分别与OA、OB交于点E、F,那么PE与PF相等吗?试猜想PE与PF的大小关系,并说明理由.
答案以及解析
1.答案:B
解析:由图形可得该几何体是圆柱;故选B.
2.答案:C
解析:与是直线被所截而成的同旁内角,当时,.
3.答案:B
解析:A选项,一天的气温和时间的关系是函数关系,
故本选项不合题意;
B选项,中的y与x的关系不是函数关系,故本选项符合题意;
C选项,在银行中利息与时间是函数关系,故本选项不合题意;
D选项,正方形的周长与面积是函数关系,故本选项不合题意.故选B.
4.答案:C
解析:
选项 分析 正误
A ×
B ×
C √
D ×
5.答案:A
解析:,.又AD平分,,,故选A.
6.答案:A
解析:,,
.
又OM平分,ON平分,
,.
.
7.答案:D
解析:的面积是1,AD是的中线,,,,,,,故选D.
8.答案:B
解析:由数轴可知,.
9.答案:D
解析:①当时,发芽的大豆粒数为382,发芽的频率为0.955,根据一次的试验频率不能估计大豆发芽的概率是0.955,故此推断错误;
②根据题表,当每批粒数足够大时,频率逐渐接近于0.950,所以估计大豆发芽的概率是0.95,此推断正确;
③若n为4000,估计大豆发芽的粒数大约为,此结论正确.故选D.
10.答案:B
解析:.在和中,
,.
11.答案:C
解析:A项,;B项应为;D项, .故选C.
12.答案:D
解析:选“责任”的有(人),故选项A正确;根据条形统计图与扇形统计图中选“奉献”的数据知调查的样本容量是,故选项B正确;选“生命”的占比,选“责任”的占比,则选“感恩”的人占比为,故选“感恩”的人数最多,故选项C正确;,故选项D错误,故选D.
13.答案:3
解析:原式,,原式.
14.答案:5
解析:由题意知直线CD是线段AB的垂直平分线,点F在直线CD上,,,.故答案为5.
15.答案:4
解析:,,即,,,,故答案为:4.
16.答案:80
解析:.
17.答案:
解析:全班共有学生(人),其中男生30人,
则该班选中一名男生当值日班长的概率是.故答案为.
18.答案:2米
解析:如图,作,,,,在和中,,,,,即(m),m.(m),m,m,m,易知m,又m,(m).马里奥在荡绳索过程中离地面的最低点的高度MN为2米.
19.答案:红方的马走一步可能的走法有14种等可能的结果,
其中有3种情况吃到了黑方棋子,
则红方的马现在走一步能吃到黑方棋子的概率是.
20.答案:(1)如图①,直线m即为所求.
(2)如图②,直线n即为所求.
21.答案:(1)则原方程可变形为关于y的方程:,解得,所以,所以.故答案为,.
(2),
移项、合并同类项,得.
令,所以,去括号,得.
移项,得.合并同类项,得.
系数化为1,得.所以.
22.答案:原式
.
当,时,原式.
23.答案:(1)见解析
(2)见解析
解析:(1)如图所示:
(2)由(1)知,OP是的平分线,
.
在与中,
,
.
24.答案:(1)见解析
(2)35°
解析:(1)证明:平分.
,
.
(2),
.
.
平分.
25.答案:如图,过点B作于点E,
,
,,
.
在与中,
,
.
m,
即村庄B到河边的距离是150m.
26.答案:(1)=.
(2).理由:如图,过点P作,,垂足分别为M,N,
则,
OP平分,,
,
,
,.
在和中,,
,.
2
同课章节目录
