2022-2023学年北师大版九年级上学期开学摸底考试数学试卷B卷(word版 含解析)
文档属性
| 名称 | 2022-2023学年北师大版九年级上学期开学摸底考试数学试卷B卷(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 665.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 20:00:31 | ||
图片预览




文档简介
九年级上学期开学摸底考试数学试卷B卷(模拟试卷)
【满分:120分】
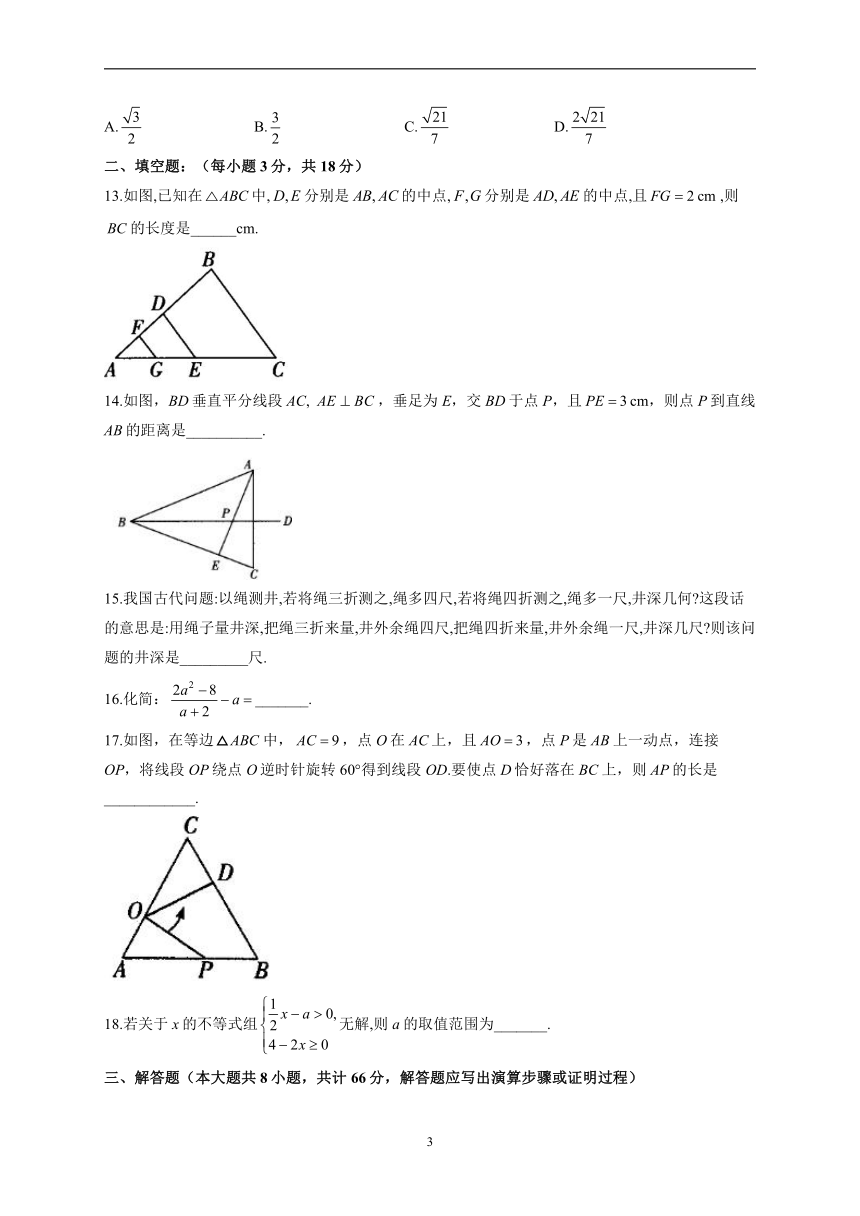
一、选择题:(本大题共12小题,每小题3分,共36分,给出的四个选项中,只有一项是符合题目要求的)
1.在直角中,,,,则AB的长为( )
A.整数 B.分数 C.无理数 D.不能确定
2.如图,将周长为8的沿BC方向平移1个单位得到,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
3.如图,是等边三角形,,,则的度数是( )
A.40° B.50° C.60° D.70°
4.某校举行关于“保护环境”的知识竞赛,共有25道题,答对一题得10分,答错(或不答)一题倒扣5分,小明参加本次竞赛,得分超过了100分,则他至少答对的题数是( )
A.17 B.16 C.15 D.12
5.某校男子足球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的平均数,中位数分别是( )
A.15.5,15.5 B.15.5,15 C.15,15.5 D.15,15
6.能被下列哪个数整除( )
A.3 B.5 C.7 D.9
7.下列计算正确的是( )
A. B.
C. D.
8.已知关于x的不等式组仅有三个整数解,则a的取值范围是( )
A. B. C. D.
9.为了能让更多人接种,某药厂的新冠疫苗生产线开足马力,24小时运转,该条生产线计划加工320万支疫苗,前五天按原计划的速度生产,五天后按原来速度的1.25倍生产,结果比原计划提前3天完成任务,设原计划每天生产x万支疫苗,则可列方程为( )
A. B.
C. D.
10.如图,在中,,连接BD,作交CD的延长线于点E,过点E作交BC的延长线于点F,且,则AB的长是( )
A.2 B.1 C. D.
11.当时,代数式的值为( )
A.5 B.-1 C.5或-1 D.0
12.如图,平行四边形ABCD的对角线AC与BD相交于点O,,垂足为E,,,,则AE的长为( )
A. B. C. D.
二、填空题:(每小题3分,共18分)
13.如图,已知在中,分别是的中点,分别是的中点,且,则的长度是______cm.
14.如图,BD垂直平分线段AC, ,垂足为E,交BD于点P,且cm,则点P到直线AB的距离是__________.
15.我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,井深几何 这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,井深几尺 则该问题的井深是_________尺.
16.化简:_______.
17.如图,在等边中,,点O在AC上,且,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是____________.
18.若关于x的不等式组无解,则a的取值范围为_______.
三、解答题(本大题共8小题,共计66分,解答题应写出演算步骤或证明过程)
19.(6分)如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为端点的线段,线段在网格线上.
(1)画出线段关于线段所在直线对称的线段(点分别为的对应点);
(2)将线段绕点顺时针旋转90°得到线段,画出线段.
20.(6分)解不等式组,并把解集在数轴上表示出来.
21.(8分)如图,求的度数.
22.(8分)某商场进货员预测一种应季T恤衫能畅销市场,就用4000元购进一批这种T恤衫,面市后果然供不应求.商场又用8800元购进了第二批这种T恤衫,所购数量是第一批购进量的2倍,但每件的进价贵了4元.
(1)该商场购进第一批、第二批T恤衫每件的进价分别是多少元?
(2)如果两批T恤衫按相同的标价销售,最后缺码的40件T恤衫按七折优惠售出,要使两批T恤衫全部售完后利润率不低于80%(不考虑其他因素),那么每件T恤衫的标价至少是多少元?
23.(8分)由于精准扶贫的措施科学得当,贫困户小颖家今年种植的草莓喜获丰收,采摘上市16天全部销售完.小颖对销售情况进行统计后发现,在该草莓上市第x天(x取整数)时,日销售量y(单位:千克)与x之间的函数关系式为草莓价格m(单位:元/千克)与x之间的函数关系如图所示.
(1)求第14天小颖家草莓的日销售量;
(2)求当时,草莓价格m与x之间的函数关系式;
(3)试比较第8天与第10天的销售金额哪天多?
24.(8分)若一个正整数能表示成两个连续偶数的平方差,则称这个正整数为“神秘数”,如,,.因此4,12,20都是“神秘数”.
(1)28和2020都是“神秘数”吗?为什么?
(2)设两个连续偶数分别为与2k(k为非负整数),由这两个连续偶数得到的“神秘数”是4的倍数吗?请说明理由.
25.(10分)如图,在平行四边形中,对角线相交于点O,分别过点作,垂足分别为平分.
(1)若,求的度数,
(2)求证:.
26.(12分)如图,在中,,,BD是的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:
(1);
(2)为等腰三角形.
答案以及解析
1.答案:C
解析:在直角中,,由勾股定理知,,故AB的长为无理数.
2.答案:C
解析:由已知可得,所以四边形ABFD的周长的周长.
3.答案:C
解析:是等边三角形,,,在和中,,,,故选C.
4.答案:B
解析:设他答对x道题.根据题意,得,解得.因为x为整数,所以x可取的量小整数为16,所以小明至少答对了16道题.故选B.
5.答案:D
解析:根据图中信息可知这些队员年龄的平均数为岁,该足球队共有队员人,则第11名和第12名的平均年龄即为年龄的中位数,即中位数为15岁,故选D.
6.答案:C
解析:,所以能被7整除.故选C.
7.答案:B
解析:与的被开方数不相同,不能合并,故A错误;,故B正确;,故C错误;,故D错误.故选B.
8.答案:A
解析:解不等式得,因为不等式组仅有三个整数解,所以这三个整数解为1,0,-1,所以,解此不等式得,故选A.
9.答案:D
解析:原计划每天生产x万支疫苗,五天后按原来速度的1.25倍生产,
五天后每天生产万支疫苗,
依题意,得.故选D.
10.答案:B
解析:四边形ABCD是平行四边形,,,,又,四边形ABDE是平行四边形,,,,,,,,.故选B.
11.答案:B
解析:原式,,且,,且,,当时,原式,故选B.
12.答案:D
解析:,,四边形ABCD是平行四边形,,
.,,.在中,,,,,故选D.
13.答案:8
解析:∵在中,分别是的中点,分别是的中点,是的中位线,.
14.答案:3cm
解析:过点P作于点F. BD垂直平分AC, ,又,点P到直线AB的距离为3cm.
15.答案:8
解析:设绳长x尺,井深y尺.由题意,得解得井深8尺.
16.答案:
解析:原式.
17.答案:6
解析:,,.在和中,,,,.
18.答案:
解析:解不等式,得.解不等式,得.
∵该不等式组无解,,解得.
19.答案:(1)如图,线段即为所求.
(2)如图,线段即为所求.
20.答案:,图见解析
解析:
①
②
不等式组的解是
21.答案:如图,
.
22.答案:(1)该商场购进第一批每件的进价为40元,第二批T恤衫每件的进价为44元
(2)每件T恤衫的标价至少是80元
解析:(1)设该商场购进第一批每件的进价为x元,第二批T恤衫每件的进价为元,
由题意得,,
解得,
经检验,是原方程的解且符合题意,
,
所以,该商场购进第一批每件的进价为40元,第二批T恤衫每件的进价为44元;
(2)两批T恤衫的数量为(件),
设每件T恤衫的标价是y元,由题意得:
,
解得
所以,每件T恤衫的标价至少是80元.
23.答案:(1)第14天小颖家草莓的日销售量是40千克
(2)
(3)第10天的销售金额多
解析:解:(1)当时,,
当时,(千克).
第14天小颖家草莓的日销售量是40千克.
(2)当时,设草莓价格m与x之间的函数关系式为,
点,在的图象上,
解得
函数关系式为.
(3)当时,,当时,,
当时,.当时,,
当时,,当时,.
第8天的销售金额为:(元),
第10天的销售金额为:(元).
,第10天的销售金额多.
24.答案:(1)28和2020都是“神秘数”.理由如下:
因为,,
所以28和2020都是“神秘数”.
(2)由这两个连续偶数得到的“神秘数”是4的倍数.理由如下:
因为,
所以由这两个连续偶数得到的“神秘数”是4的倍数.
25.答案:(1)40°
(2)见解析
解析:(1).
.
平分.
∵四边形是平行四边形,,
.
(2)证明:与交于点
.
在和中
.
26.答案:证明:(1),,
.
又BD是的平分线,,
,
,又E是AB的中点,
,即.
(2),,
FE垂直平分AB,
,.
又,
.
又,
,
,
,即为等腰三角形.
2
【满分:120分】
一、选择题:(本大题共12小题,每小题3分,共36分,给出的四个选项中,只有一项是符合题目要求的)
1.在直角中,,,,则AB的长为( )
A.整数 B.分数 C.无理数 D.不能确定
2.如图,将周长为8的沿BC方向平移1个单位得到,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
3.如图,是等边三角形,,,则的度数是( )
A.40° B.50° C.60° D.70°
4.某校举行关于“保护环境”的知识竞赛,共有25道题,答对一题得10分,答错(或不答)一题倒扣5分,小明参加本次竞赛,得分超过了100分,则他至少答对的题数是( )
A.17 B.16 C.15 D.12
5.某校男子足球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的平均数,中位数分别是( )
A.15.5,15.5 B.15.5,15 C.15,15.5 D.15,15
6.能被下列哪个数整除( )
A.3 B.5 C.7 D.9
7.下列计算正确的是( )
A. B.
C. D.
8.已知关于x的不等式组仅有三个整数解,则a的取值范围是( )
A. B. C. D.
9.为了能让更多人接种,某药厂的新冠疫苗生产线开足马力,24小时运转,该条生产线计划加工320万支疫苗,前五天按原计划的速度生产,五天后按原来速度的1.25倍生产,结果比原计划提前3天完成任务,设原计划每天生产x万支疫苗,则可列方程为( )
A. B.
C. D.
10.如图,在中,,连接BD,作交CD的延长线于点E,过点E作交BC的延长线于点F,且,则AB的长是( )
A.2 B.1 C. D.
11.当时,代数式的值为( )
A.5 B.-1 C.5或-1 D.0
12.如图,平行四边形ABCD的对角线AC与BD相交于点O,,垂足为E,,,,则AE的长为( )
A. B. C. D.
二、填空题:(每小题3分,共18分)
13.如图,已知在中,分别是的中点,分别是的中点,且,则的长度是______cm.
14.如图,BD垂直平分线段AC, ,垂足为E,交BD于点P,且cm,则点P到直线AB的距离是__________.
15.我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,井深几何 这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,井深几尺 则该问题的井深是_________尺.
16.化简:_______.
17.如图,在等边中,,点O在AC上,且,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是____________.
18.若关于x的不等式组无解,则a的取值范围为_______.
三、解答题(本大题共8小题,共计66分,解答题应写出演算步骤或证明过程)
19.(6分)如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为端点的线段,线段在网格线上.
(1)画出线段关于线段所在直线对称的线段(点分别为的对应点);
(2)将线段绕点顺时针旋转90°得到线段,画出线段.
20.(6分)解不等式组,并把解集在数轴上表示出来.
21.(8分)如图,求的度数.
22.(8分)某商场进货员预测一种应季T恤衫能畅销市场,就用4000元购进一批这种T恤衫,面市后果然供不应求.商场又用8800元购进了第二批这种T恤衫,所购数量是第一批购进量的2倍,但每件的进价贵了4元.
(1)该商场购进第一批、第二批T恤衫每件的进价分别是多少元?
(2)如果两批T恤衫按相同的标价销售,最后缺码的40件T恤衫按七折优惠售出,要使两批T恤衫全部售完后利润率不低于80%(不考虑其他因素),那么每件T恤衫的标价至少是多少元?
23.(8分)由于精准扶贫的措施科学得当,贫困户小颖家今年种植的草莓喜获丰收,采摘上市16天全部销售完.小颖对销售情况进行统计后发现,在该草莓上市第x天(x取整数)时,日销售量y(单位:千克)与x之间的函数关系式为草莓价格m(单位:元/千克)与x之间的函数关系如图所示.
(1)求第14天小颖家草莓的日销售量;
(2)求当时,草莓价格m与x之间的函数关系式;
(3)试比较第8天与第10天的销售金额哪天多?
24.(8分)若一个正整数能表示成两个连续偶数的平方差,则称这个正整数为“神秘数”,如,,.因此4,12,20都是“神秘数”.
(1)28和2020都是“神秘数”吗?为什么?
(2)设两个连续偶数分别为与2k(k为非负整数),由这两个连续偶数得到的“神秘数”是4的倍数吗?请说明理由.
25.(10分)如图,在平行四边形中,对角线相交于点O,分别过点作,垂足分别为平分.
(1)若,求的度数,
(2)求证:.
26.(12分)如图,在中,,,BD是的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:
(1);
(2)为等腰三角形.
答案以及解析
1.答案:C
解析:在直角中,,由勾股定理知,,故AB的长为无理数.
2.答案:C
解析:由已知可得,所以四边形ABFD的周长的周长.
3.答案:C
解析:是等边三角形,,,在和中,,,,故选C.
4.答案:B
解析:设他答对x道题.根据题意,得,解得.因为x为整数,所以x可取的量小整数为16,所以小明至少答对了16道题.故选B.
5.答案:D
解析:根据图中信息可知这些队员年龄的平均数为岁,该足球队共有队员人,则第11名和第12名的平均年龄即为年龄的中位数,即中位数为15岁,故选D.
6.答案:C
解析:,所以能被7整除.故选C.
7.答案:B
解析:与的被开方数不相同,不能合并,故A错误;,故B正确;,故C错误;,故D错误.故选B.
8.答案:A
解析:解不等式得,因为不等式组仅有三个整数解,所以这三个整数解为1,0,-1,所以,解此不等式得,故选A.
9.答案:D
解析:原计划每天生产x万支疫苗,五天后按原来速度的1.25倍生产,
五天后每天生产万支疫苗,
依题意,得.故选D.
10.答案:B
解析:四边形ABCD是平行四边形,,,,又,四边形ABDE是平行四边形,,,,,,,,.故选B.
11.答案:B
解析:原式,,且,,且,,当时,原式,故选B.
12.答案:D
解析:,,四边形ABCD是平行四边形,,
.,,.在中,,,,,故选D.
13.答案:8
解析:∵在中,分别是的中点,分别是的中点,是的中位线,.
14.答案:3cm
解析:过点P作于点F. BD垂直平分AC, ,又,点P到直线AB的距离为3cm.
15.答案:8
解析:设绳长x尺,井深y尺.由题意,得解得井深8尺.
16.答案:
解析:原式.
17.答案:6
解析:,,.在和中,,,,.
18.答案:
解析:解不等式,得.解不等式,得.
∵该不等式组无解,,解得.
19.答案:(1)如图,线段即为所求.
(2)如图,线段即为所求.
20.答案:,图见解析
解析:
①
②
不等式组的解是
21.答案:如图,
.
22.答案:(1)该商场购进第一批每件的进价为40元,第二批T恤衫每件的进价为44元
(2)每件T恤衫的标价至少是80元
解析:(1)设该商场购进第一批每件的进价为x元,第二批T恤衫每件的进价为元,
由题意得,,
解得,
经检验,是原方程的解且符合题意,
,
所以,该商场购进第一批每件的进价为40元,第二批T恤衫每件的进价为44元;
(2)两批T恤衫的数量为(件),
设每件T恤衫的标价是y元,由题意得:
,
解得
所以,每件T恤衫的标价至少是80元.
23.答案:(1)第14天小颖家草莓的日销售量是40千克
(2)
(3)第10天的销售金额多
解析:解:(1)当时,,
当时,(千克).
第14天小颖家草莓的日销售量是40千克.
(2)当时,设草莓价格m与x之间的函数关系式为,
点,在的图象上,
解得
函数关系式为.
(3)当时,,当时,,
当时,.当时,,
当时,,当时,.
第8天的销售金额为:(元),
第10天的销售金额为:(元).
,第10天的销售金额多.
24.答案:(1)28和2020都是“神秘数”.理由如下:
因为,,
所以28和2020都是“神秘数”.
(2)由这两个连续偶数得到的“神秘数”是4的倍数.理由如下:
因为,
所以由这两个连续偶数得到的“神秘数”是4的倍数.
25.答案:(1)40°
(2)见解析
解析:(1).
.
平分.
∵四边形是平行四边形,,
.
(2)证明:与交于点
.
在和中
.
26.答案:证明:(1),,
.
又BD是的平分线,,
,
,又E是AB的中点,
,即.
(2),,
FE垂直平分AB,
,.
又,
.
又,
,
,
,即为等腰三角形.
2
同课章节目录
