1.5.2 科学记数法 课件(共25张PPT)
文档属性
| 名称 | 1.5.2 科学记数法 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
1.5.2 科学记数法
人教版七年级上册
教学目标
教学目标: 1.利用10的乘方,进行科学记数,会用科学记数法表示大
于10的数,会解决与科学记数法有关的实际问题.
2.体会科学记数法的好处和化繁为简的方法.
教学重点: 用科学记数法表示大于10的数的方法.
教学难点: 探究用科学记数法表示大于10的数的方法.
新知导入
情境引入
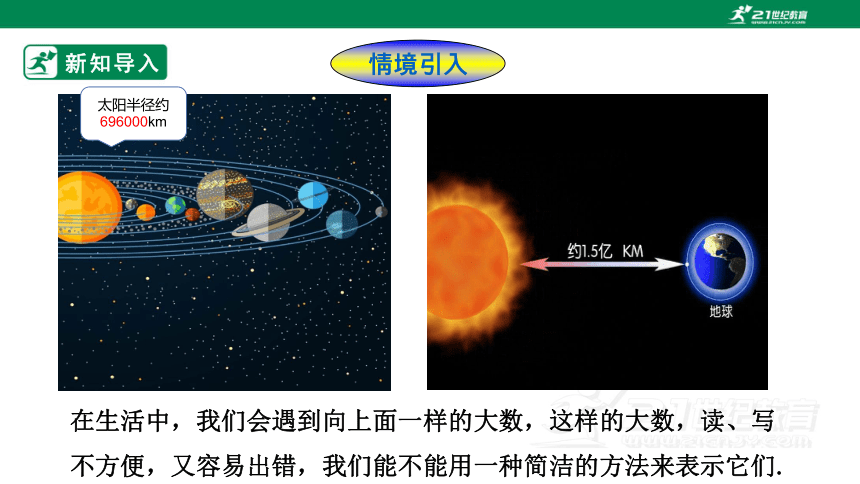
太阳半径约696000km
在生活中,我们会遇到向上面一样的大数,这样的大数,读、写不方便,又容易出错,我们能不能用一种简洁的方法来表示它们.
新知讲解
合作学习
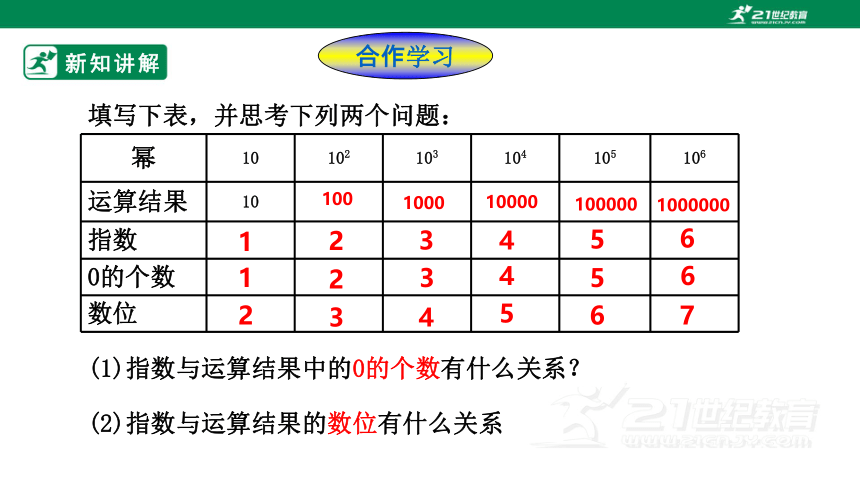
幂 10 102 103 104 105 106
运算结果 10
指数
0的个数
数位
1
(1)指数与运算结果中的0的个数有什么关系?
(2)指数与运算结果的数位有什么关系
填写下表,并思考下列两个问题:
1
2
2
3
2
4
3
3
4
4
5
5
6
5
7
6
6
100
1000
10000
100000
1000000
(1)指数与运算结果中的0的个数相等.
(2)指数比运算结果的数位小1.
从上表可知:
把下列各数写成10的幂的形式:
100 ,10000,10000000,
100=10╳10=102
10000=10╳10╳10╳10=104
100000000=10╳10╳10╳10 ╳ 10╳10╳10=107
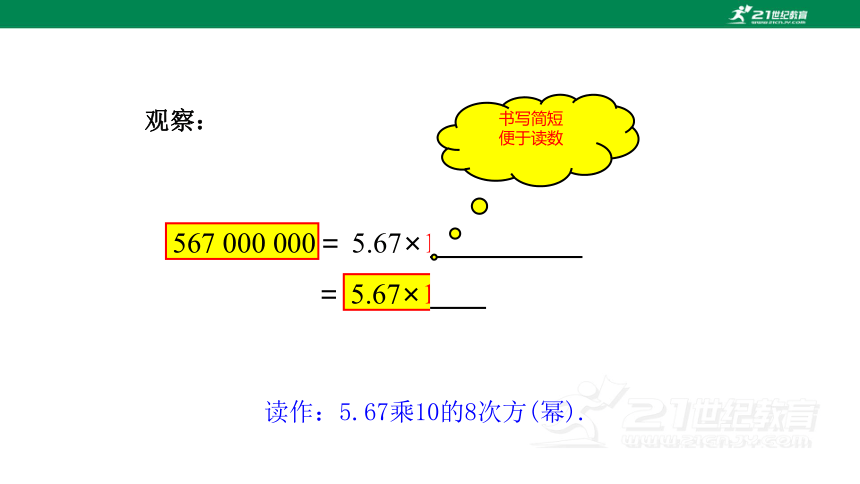
567 000 000= 5.67×100 000 000
观察:
= 5.67×108
读作:5.67乘10的8次方(幂).
书写简短
便于读数
一般地,10的次幂等于 (在1的后面n个0),所以
可以利用10的乘方表示一些大数,例如
567000000=5.67╳100000000=5.67 ╳108 ,
读作“5.67乘10的8次方(幂).
这样不仅可以使书写简短,现时还便于读数.
提炼概念
把一个大于10的数都可以记成a×10n的形式(其中a大于或等于1且小于10, n是正整数),这种记数方法叫做科学记数法.
对于小于10的数,也可以类似表示,例如
-567000000=-5.67╳100000000=-5.67 ╳108
典例精讲
例5:用科学记数法表示下列各数:
1000 000,57000 000,-123000 000 000
-123 000 000 000=-1.23×1011
57000 000=5.7×107,
解:1000 000=106,
思考:
上面的式子中,等号左边整数的位数与右边10的指数有什么关系?
用科学记数法表示一个n位整数,其中10的指数是 .
n-1
科学记数法a×10n(1≤a<10),中a与n的确定:
(4)表示一个带有单位的数时,其表示的结果也应带有单位,并且前后一致.
(3)科学记数法是一种记数方法,不改变数的性质和大小;用科学记数法表.
(2)n的值比原数的整数位数少1.
(1)a就是把原数的小数点移动到左边第1个不是0的数字后面所得到的数;
归纳概念
思考:下列用科学记数法表示的数,原数是什么?
解:(1)因为10的指数是5,所以原数的整数部分有6位,得原数为600000;
(1)6×105; (2)1.234×1011; (3)-1.27×107.
(2)因为10的指数是11,所以原数的整数部分有12位,把1.234的小数点向右移动11位,得原数为123400000000;
(3)因为10的指数是7,所以原数的整数部分有8位,把1.234的小数点向右移动7位,得原数为-12700000;
解法二:
(1)6×105
(2)1.234×1011
=123400000000
(3)-1.27×107
=-1.27×10000000
=-12700000
=1.234×100000000000
=6×100000
=600000
1.把科学记数法表示的数a×10n ,还原成原来的数时,只需把a中的小数点向右移动n位,并去掉乘号和10n即可,若向右移动的位数不够,应用0补足.
还原用科学记数法表示的数:
课堂练习
1.在以下各数中,最大的数为( )
A.7.2 × 108 B.2.5 × 109
C.9.9 × 108 D.1 × 107
2. 1.414×10n+1是用科学记数法表示的数,则它的原数是( )位整数.
A.n-1 B.n C.n+1 D.n+2
B
D
(3)10 000 000=10×106 ( )
(1)5 629 000=5.629×106 ( )
3.判断下列科学记数法的正误并改正.
√
×
×
(2)45 000 000=0.45×108 ( )
4. 一个数是2500000000,甲把它记为25亿,乙把它记为25×108,丙把它记为2.5×108,丁把它记为0.25×108.他们的记法谁对谁错?
解:甲的记法正确,乙、丙、丁错误
5.下列用科学记数法表示的数,原来各是什么数?
5×106 1.5×105 2.03×107 -1.06×105
解:5×106
=5×1000000
=5000000
1.5×105
=1.5×100000
=150000
2.03×107
=2.03×10000000
=20300000
-1.06×105
=-1.06×100000
=106000
D
6.已知光的速度为300 000 000米/秒,太阳光到达地球的时间大约是500秒,试计算太阳与地球的距离大约为多少千米.(结果用科学记数法表示)
解:太阳与地球的距离
=300 000 000×500
=150 000 000 000米=1.5×108千米
答:太阳与地球的距离大约为1.5×108千米.
7. 一个正常人的平均心跳速率约为每分70次,一年大约跳多
少次?用科学记数法表示这一结果,一个正常人一生心跳
次数能达到1亿次吗?请说明理由.
解:因为1 年=365 天=365×24×60 分,
所以一年心跳次数约为:
365×24×60×70=
=3.679 2×107(次);
108÷( 3.6792×107)
≈2.7(年),
因为心跳达到1亿次需要的时间是:
所以一个正常人一生心跳次数能达到1亿次.
36 792 000
课堂总结
2.用科学计数法表示较大的数应注意以下两点:
1≤a<10
当大数是大于10的整数时,n为整数位减去1.
3.灵活运用科学计数法,注意解题技巧,总结解题规律.
1.把一个大于10的数都可以记成a×10n的形式(其中a大于或等于1且小于10, n是正整数),这种记数方法叫做科学记数法.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.5.2 科学记数法
人教版七年级上册
教学目标
教学目标: 1.利用10的乘方,进行科学记数,会用科学记数法表示大
于10的数,会解决与科学记数法有关的实际问题.
2.体会科学记数法的好处和化繁为简的方法.
教学重点: 用科学记数法表示大于10的数的方法.
教学难点: 探究用科学记数法表示大于10的数的方法.
新知导入
情境引入
太阳半径约696000km
在生活中,我们会遇到向上面一样的大数,这样的大数,读、写不方便,又容易出错,我们能不能用一种简洁的方法来表示它们.
新知讲解
合作学习
幂 10 102 103 104 105 106
运算结果 10
指数
0的个数
数位
1
(1)指数与运算结果中的0的个数有什么关系?
(2)指数与运算结果的数位有什么关系
填写下表,并思考下列两个问题:
1
2
2
3
2
4
3
3
4
4
5
5
6
5
7
6
6
100
1000
10000
100000
1000000
(1)指数与运算结果中的0的个数相等.
(2)指数比运算结果的数位小1.
从上表可知:
把下列各数写成10的幂的形式:
100 ,10000,10000000,
100=10╳10=102
10000=10╳10╳10╳10=104
100000000=10╳10╳10╳10 ╳ 10╳10╳10=107
567 000 000= 5.67×100 000 000
观察:
= 5.67×108
读作:5.67乘10的8次方(幂).
书写简短
便于读数
一般地,10的次幂等于 (在1的后面n个0),所以
可以利用10的乘方表示一些大数,例如
567000000=5.67╳100000000=5.67 ╳108 ,
读作“5.67乘10的8次方(幂).
这样不仅可以使书写简短,现时还便于读数.
提炼概念
把一个大于10的数都可以记成a×10n的形式(其中a大于或等于1且小于10, n是正整数),这种记数方法叫做科学记数法.
对于小于10的数,也可以类似表示,例如
-567000000=-5.67╳100000000=-5.67 ╳108
典例精讲
例5:用科学记数法表示下列各数:
1000 000,57000 000,-123000 000 000
-123 000 000 000=-1.23×1011
57000 000=5.7×107,
解:1000 000=106,
思考:
上面的式子中,等号左边整数的位数与右边10的指数有什么关系?
用科学记数法表示一个n位整数,其中10的指数是 .
n-1
科学记数法a×10n(1≤a<10),中a与n的确定:
(4)表示一个带有单位的数时,其表示的结果也应带有单位,并且前后一致.
(3)科学记数法是一种记数方法,不改变数的性质和大小;用科学记数法表.
(2)n的值比原数的整数位数少1.
(1)a就是把原数的小数点移动到左边第1个不是0的数字后面所得到的数;
归纳概念
思考:下列用科学记数法表示的数,原数是什么?
解:(1)因为10的指数是5,所以原数的整数部分有6位,得原数为600000;
(1)6×105; (2)1.234×1011; (3)-1.27×107.
(2)因为10的指数是11,所以原数的整数部分有12位,把1.234的小数点向右移动11位,得原数为123400000000;
(3)因为10的指数是7,所以原数的整数部分有8位,把1.234的小数点向右移动7位,得原数为-12700000;
解法二:
(1)6×105
(2)1.234×1011
=123400000000
(3)-1.27×107
=-1.27×10000000
=-12700000
=1.234×100000000000
=6×100000
=600000
1.把科学记数法表示的数a×10n ,还原成原来的数时,只需把a中的小数点向右移动n位,并去掉乘号和10n即可,若向右移动的位数不够,应用0补足.
还原用科学记数法表示的数:
课堂练习
1.在以下各数中,最大的数为( )
A.7.2 × 108 B.2.5 × 109
C.9.9 × 108 D.1 × 107
2. 1.414×10n+1是用科学记数法表示的数,则它的原数是( )位整数.
A.n-1 B.n C.n+1 D.n+2
B
D
(3)10 000 000=10×106 ( )
(1)5 629 000=5.629×106 ( )
3.判断下列科学记数法的正误并改正.
√
×
×
(2)45 000 000=0.45×108 ( )
4. 一个数是2500000000,甲把它记为25亿,乙把它记为25×108,丙把它记为2.5×108,丁把它记为0.25×108.他们的记法谁对谁错?
解:甲的记法正确,乙、丙、丁错误
5.下列用科学记数法表示的数,原来各是什么数?
5×106 1.5×105 2.03×107 -1.06×105
解:5×106
=5×1000000
=5000000
1.5×105
=1.5×100000
=150000
2.03×107
=2.03×10000000
=20300000
-1.06×105
=-1.06×100000
=106000
D
6.已知光的速度为300 000 000米/秒,太阳光到达地球的时间大约是500秒,试计算太阳与地球的距离大约为多少千米.(结果用科学记数法表示)
解:太阳与地球的距离
=300 000 000×500
=150 000 000 000米=1.5×108千米
答:太阳与地球的距离大约为1.5×108千米.
7. 一个正常人的平均心跳速率约为每分70次,一年大约跳多
少次?用科学记数法表示这一结果,一个正常人一生心跳
次数能达到1亿次吗?请说明理由.
解:因为1 年=365 天=365×24×60 分,
所以一年心跳次数约为:
365×24×60×70=
=3.679 2×107(次);
108÷( 3.6792×107)
≈2.7(年),
因为心跳达到1亿次需要的时间是:
所以一个正常人一生心跳次数能达到1亿次.
36 792 000
课堂总结
2.用科学计数法表示较大的数应注意以下两点:
1≤a<10
当大数是大于10的整数时,n为整数位减去1.
3.灵活运用科学计数法,注意解题技巧,总结解题规律.
1.把一个大于10的数都可以记成a×10n的形式(其中a大于或等于1且小于10, n是正整数),这种记数方法叫做科学记数法.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
