人教版九年级上册数学22.3实际问题与二次函数 同步练习(word版 含简单答案)
文档属性
| 名称 | 人教版九年级上册数学22.3实际问题与二次函数 同步练习(word版 含简单答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 139.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览

文档简介
人教版九年级上册数学22.3 实际问题与二次函数同步练习
一、单选题
1.板球是以击球、投球和接球为主的运动,该项目主要锻炼手眼的协调能力,集上肢动作控制能力、技巧与力量为一体的综合性运动.如图,是运动员击球过程中板球运动的轨迹示意图,板球在点A处击出,落地前的点B处被对方接住,已知板球经过的路线是抛物线,其表达式为y=-x2+x+1,则板球运行中离地面的最大高度为( )
A.1m B.m C.m D.4m
2.为方便市民进行垃圾分类投放,某环保公司第一个月投放a个垃圾桶,计划第三个月投放垃圾桶y个,设该公司第二、三两个月投放垃圾桶数量的月平均增长率为x,那么y与x的函数关系是( )
A. B. C. D.
3.为响应国家的惠民政策,某种口罩原价每箱100元,经过两次降价后每箱81元.设平均每次降价的百分率都为x,则x满足( )
A.81(1+2x)= 100 B.100(1-2x)=81
C.81(1+x)=100 D.100(1-x)=81
4.某商场降价销售一批名牌衬衫,已知所获得利润(元)与降价金额(元)之间的关系是,则获利最多为()
A.元 B.元 C.元 D.元
5.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅游团的人数每增加一人,每人的单价就降低10元,若这个旅行社要获得最大营业额,则这个旅游团的人数是( )
A.55 B.56 C.57 D.58
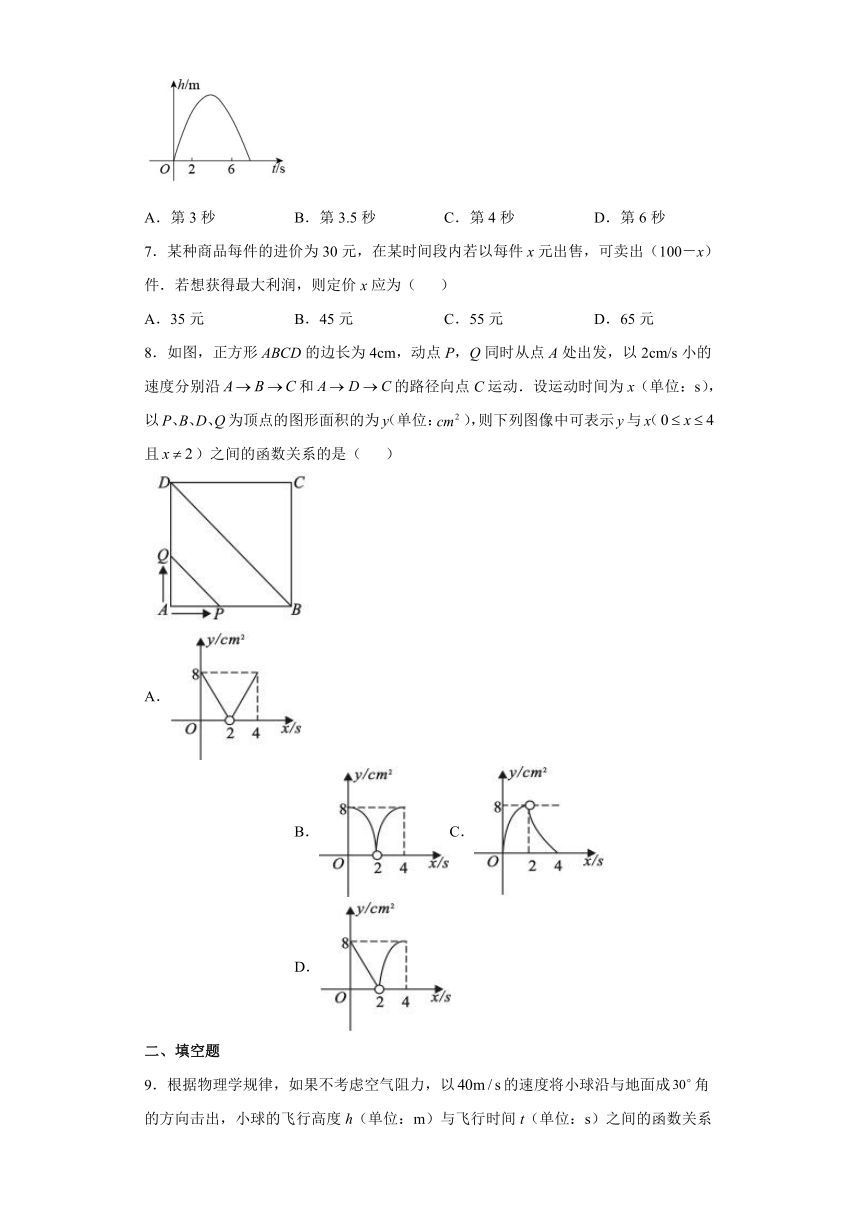
6.竖直向上发射的小球的高度关于运动时间的函数表达式为,其图象如图所示,若小球发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( )
A.第3秒 B.第3.5秒 C.第4秒 D.第6秒
7.某种商品每件的进价为30元,在某时间段内若以每件x元出售,可卖出(100-x)件.若想获得最大利润,则定价x应为( )
A.35元 B.45元 C.55元 D.65元
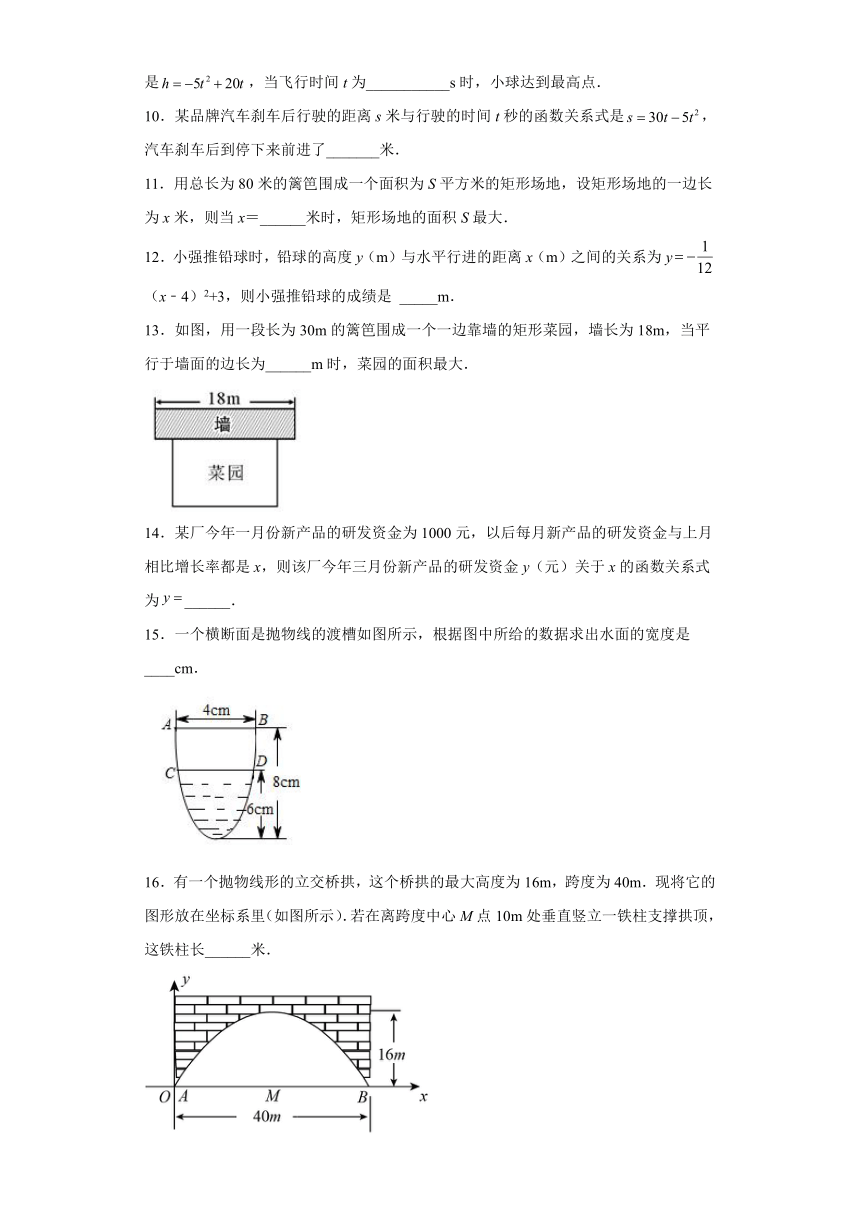
8.如图,正方形ABCD的边长为4cm,动点P,Q同时从点A处出发,以2cm/s小的速度分别沿和的路径向点C运动.设运动时间为x(单位:s),以P、B、D、Q为顶点的图形面积的为y(单位:),则下列图像中可表示y与x(且)之间的函数关系的是( )
A. B.C. D.
二、填空题
9.根据物理学规律,如果不考虑空气阻力,以的速度将小球沿与地面成角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是,当飞行时间t为___________s时,小球达到最高点.
10.某品牌汽车刹车后行驶的距离s米与行驶的时间t秒的函数关系式是,汽车刹车后到停下来前进了_______米.
11.用总长为80米的篱笆围成一个面积为S平方米的矩形场地,设矩形场地的一边长为x米,则当x=______米时,矩形场地的面积S最大.
12.小强推铅球时,铅球的高度y(m)与水平行进的距离x(m)之间的关系为y(x﹣4)2+3,则小强推铅球的成绩是 _____m.
13.如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,当平行于墙面的边长为______m时,菜园的面积最大.
14.某厂今年一月份新产品的研发资金为1000元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为______.
15.一个横断面是抛物线的渡槽如图所示,根据图中所给的数据求出水面的宽度是____cm.
16.有一个抛物线形的立交桥拱,这个桥拱的最大高度为16m,跨度为40m.现将它的图形放在坐标系里(如图所示).若在离跨度中心M点10m处垂直竖立一铁柱支撑拱顶,这铁柱长______米.
三、解答题
17.某商场购进一批服装,进价为每件30元,售价为每件50元,每周可卖出300件,如果每件商品的售价每涨1元,则每周少卖出10件(每件售价不能高于70元).设每件商品的售价上涨x元,每周的销售量为y件,每周的销售利润为w元.
(1)写出y与x的函数关系式,并求出x的取值范围;
(2)写出w与x的函数关系式,并求出当x为何值时,w取得最大值,最大值为多少
18.某商场销售一种进价为每件20元的日用商品,经调查发现,该商品每天的销售量y(件)与销售单价(元)满足y=﹣10x+400,设销售这种商品每天的利润为w(元).
(1)求w与x之间的函数关系式;
(2)在保证销售量尽可能大的前提下,该商场每天还想获得750元的利润,应将销售单价定为多少元?
(3)当每天销售量不少于30件,且销售单价至少为35元时,该商场每天获得的最大利润是多少?
19.商场销售一款新型的钢笔,进价为140元/支.销售中发现这种钢笔每天的销售量(支)与售价(元/支)之间满足一次函数关系.
(1)请写出商场销售这种钢笔每天的利润(元)与售价(元/支)之间的函数关系式.
(2)商场每天销售这种钢笔的利润能否达到3000元?如果能,求出此时的销售价格;如果不能,说明理由.
20.如图,一张正方形纸板的边长为8cm,将它割去一个正方形,留下四个全等的直角三角形(图中阴影部分).设AE=BF=CG=DH=x(cm),阴影部分的面积为y(cm2).
(1)求y关于x的函数解析式并写出x的取值范围;
(2)当x取何值时,阴影部分的面积最大,最大面积是多少.
试卷第1页,共3页
参考答案:
1.B
2.A
3.D
4.D
5.A
6.C
7.D
8.B
9.2
10.45
11.20
12.10
13.15
14.
15.2
16.12
17.(1),
(2)w与x的函数关系式为w= 10x2+100x+6000,x=5时,W取最大值,最大值为6250元
18.(1)W=﹣10x2+600x﹣8000
(2)应将销售单价定为25元
(3)该商场每天获得的最大利润是750元
19.(1)
(2)不能,理由见解析
20.(1)(0<x<8)
(2)当x=4时,阴影部分面积最大值为32cm2.
答案第1页,共2页
一、单选题
1.板球是以击球、投球和接球为主的运动,该项目主要锻炼手眼的协调能力,集上肢动作控制能力、技巧与力量为一体的综合性运动.如图,是运动员击球过程中板球运动的轨迹示意图,板球在点A处击出,落地前的点B处被对方接住,已知板球经过的路线是抛物线,其表达式为y=-x2+x+1,则板球运行中离地面的最大高度为( )
A.1m B.m C.m D.4m
2.为方便市民进行垃圾分类投放,某环保公司第一个月投放a个垃圾桶,计划第三个月投放垃圾桶y个,设该公司第二、三两个月投放垃圾桶数量的月平均增长率为x,那么y与x的函数关系是( )
A. B. C. D.
3.为响应国家的惠民政策,某种口罩原价每箱100元,经过两次降价后每箱81元.设平均每次降价的百分率都为x,则x满足( )
A.81(1+2x)= 100 B.100(1-2x)=81
C.81(1+x)=100 D.100(1-x)=81
4.某商场降价销售一批名牌衬衫,已知所获得利润(元)与降价金额(元)之间的关系是,则获利最多为()
A.元 B.元 C.元 D.元
5.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅游团的人数每增加一人,每人的单价就降低10元,若这个旅行社要获得最大营业额,则这个旅游团的人数是( )
A.55 B.56 C.57 D.58
6.竖直向上发射的小球的高度关于运动时间的函数表达式为,其图象如图所示,若小球发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( )
A.第3秒 B.第3.5秒 C.第4秒 D.第6秒
7.某种商品每件的进价为30元,在某时间段内若以每件x元出售,可卖出(100-x)件.若想获得最大利润,则定价x应为( )
A.35元 B.45元 C.55元 D.65元
8.如图,正方形ABCD的边长为4cm,动点P,Q同时从点A处出发,以2cm/s小的速度分别沿和的路径向点C运动.设运动时间为x(单位:s),以P、B、D、Q为顶点的图形面积的为y(单位:),则下列图像中可表示y与x(且)之间的函数关系的是( )
A. B.C. D.
二、填空题
9.根据物理学规律,如果不考虑空气阻力,以的速度将小球沿与地面成角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是,当飞行时间t为___________s时,小球达到最高点.
10.某品牌汽车刹车后行驶的距离s米与行驶的时间t秒的函数关系式是,汽车刹车后到停下来前进了_______米.
11.用总长为80米的篱笆围成一个面积为S平方米的矩形场地,设矩形场地的一边长为x米,则当x=______米时,矩形场地的面积S最大.
12.小强推铅球时,铅球的高度y(m)与水平行进的距离x(m)之间的关系为y(x﹣4)2+3,则小强推铅球的成绩是 _____m.
13.如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,当平行于墙面的边长为______m时,菜园的面积最大.
14.某厂今年一月份新产品的研发资金为1000元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为______.
15.一个横断面是抛物线的渡槽如图所示,根据图中所给的数据求出水面的宽度是____cm.
16.有一个抛物线形的立交桥拱,这个桥拱的最大高度为16m,跨度为40m.现将它的图形放在坐标系里(如图所示).若在离跨度中心M点10m处垂直竖立一铁柱支撑拱顶,这铁柱长______米.
三、解答题
17.某商场购进一批服装,进价为每件30元,售价为每件50元,每周可卖出300件,如果每件商品的售价每涨1元,则每周少卖出10件(每件售价不能高于70元).设每件商品的售价上涨x元,每周的销售量为y件,每周的销售利润为w元.
(1)写出y与x的函数关系式,并求出x的取值范围;
(2)写出w与x的函数关系式,并求出当x为何值时,w取得最大值,最大值为多少
18.某商场销售一种进价为每件20元的日用商品,经调查发现,该商品每天的销售量y(件)与销售单价(元)满足y=﹣10x+400,设销售这种商品每天的利润为w(元).
(1)求w与x之间的函数关系式;
(2)在保证销售量尽可能大的前提下,该商场每天还想获得750元的利润,应将销售单价定为多少元?
(3)当每天销售量不少于30件,且销售单价至少为35元时,该商场每天获得的最大利润是多少?
19.商场销售一款新型的钢笔,进价为140元/支.销售中发现这种钢笔每天的销售量(支)与售价(元/支)之间满足一次函数关系.
(1)请写出商场销售这种钢笔每天的利润(元)与售价(元/支)之间的函数关系式.
(2)商场每天销售这种钢笔的利润能否达到3000元?如果能,求出此时的销售价格;如果不能,说明理由.
20.如图,一张正方形纸板的边长为8cm,将它割去一个正方形,留下四个全等的直角三角形(图中阴影部分).设AE=BF=CG=DH=x(cm),阴影部分的面积为y(cm2).
(1)求y关于x的函数解析式并写出x的取值范围;
(2)当x取何值时,阴影部分的面积最大,最大面积是多少.
试卷第1页,共3页
参考答案:
1.B
2.A
3.D
4.D
5.A
6.C
7.D
8.B
9.2
10.45
11.20
12.10
13.15
14.
15.2
16.12
17.(1),
(2)w与x的函数关系式为w= 10x2+100x+6000,x=5时,W取最大值,最大值为6250元
18.(1)W=﹣10x2+600x﹣8000
(2)应将销售单价定为25元
(3)该商场每天获得的最大利润是750元
19.(1)
(2)不能,理由见解析
20.(1)(0<x<8)
(2)当x=4时,阴影部分面积最大值为32cm2.
答案第1页,共2页
同课章节目录
