北师大版数学八年级上册 第1章勾股定理 中考真题训练(word版 含解析)
文档属性
| 名称 | 北师大版数学八年级上册 第1章勾股定理 中考真题训练(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 124.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 20:19:57 | ||
图片预览

文档简介
勾股定理
一、选择题
1.(2021山西)在勾股定理的学习过程中,我们已经学会了运用如图所示的图形,验证著名的勾股定理,这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律,它体现的数学思想是 ( )
A.统计思想 B.分类思想
C.数形结合思想 D.函数思想
2.(2021滨州)在Rt△ABC中,若∠C=90°,AC=3,BC=4,则点C到直线AB的距离为( )
A.3 B.4 C.5 D.2.4
3.(2020巴中)《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何 ”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子 ( )
A.4尺 B.4.55尺 C.5尺 D.5.55尺
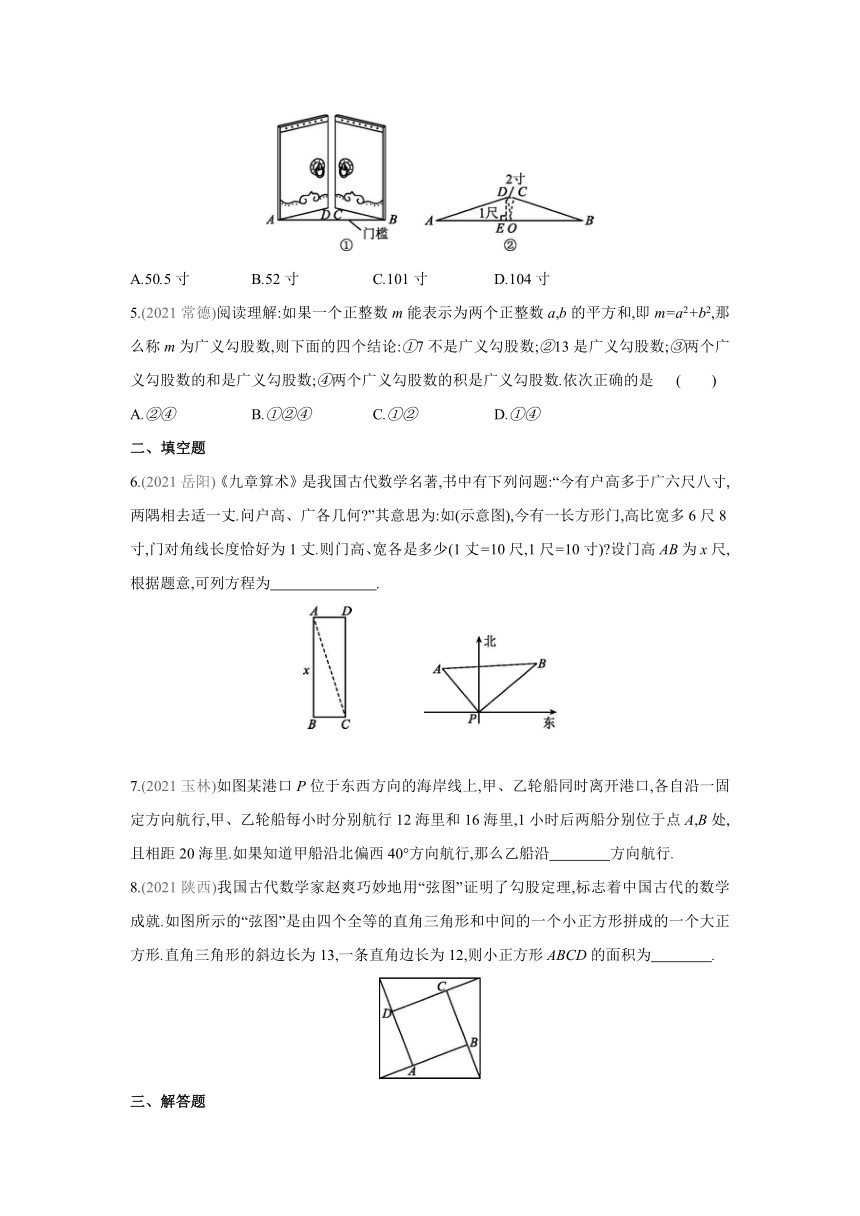
4.(2020广西)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意是:如①②(图②为图①的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是 ( )
A.50.5寸 B.52寸 C.101寸 D.104寸
5.(2021常德)阅读理解:如果一个正整数m能表示为两个正整数a,b的平方和,即m=a2+b2,那么称m为广义勾股数,则下面的四个结论:①7不是广义勾股数;②13是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数.依次正确的是 ( )
A.②④ B.①②④ C.①② D.①④
二、填空题
6.(2021岳阳)《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何 ”其意思为:如(示意图),今有一长方形门,高比宽多6尺8寸,门对角线长度恰好为1丈.则门高、宽各是多少(1丈=10尺,1尺=10寸) 设门高AB为x尺,根据题意,可列方程为 .
7.(2021玉林)如图某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里.如果知道甲船沿北偏西40°方向航行,那么乙船沿 方向航行.
8.(2021陕西)我国古代数学家赵爽巧妙地用“弦图”证明了勾股定理,标志着中国古代的数学成就.如图所示的“弦图”是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形.直角三角形的斜边长为13,一条直角边长为12,则小正方形ABCD的面积为 .
三、解答题
9.(2020山西改编)阅读与思考:
下面是小宇同学的数学日记,请仔细阅读,并完成相应的任务.
×年×月×日 星期日
没有直角尺也能作出直角
今天,我在书店一本书上看到下面材料:木工师傅有一块如①所示的四边形木板,他已经在木板上画出一条裁割线AB,现根据木板的情况,要过AB上的一点C,作出AB的垂线,用锯子进行裁割,然而手头没有直角尺,怎么办呢
办法一:如图①,可利用一把有刻度的直尺在AB上量出CD=30 cm,然后分别以D,C为圆心,以50 cm与40 cm为半径画圆弧,两弧相交于点E,作直线CE,则∠DCE必为90°.
办法二:如图②,可以取一根笔直的木棒,用铅笔在木棒上点出M,N两点,然后把木棒斜放在木板上,使点M与点C重合,用铅笔在木板上将点N对应的位置标记
为点Q,保持点N不动,将木棒绕点N旋转,使点M落在AB上,在木板上将点M对应的位置标记为点R.然后将RQ延长,在延长线上截取线段QS=MN,得到点S,作直线SC,则∠RCS=90°.
任务:
(1)填空:“办法一”依据的一个数学定理是 ;
(2)根据“办法二”的操作过程,试说明∠RCS=90°.
答案
勾股定理
1.C
2.D 过点C作CD⊥AB于点D,如图所示.
因为∠ACB=90°,AC=3,BC=4,
所以AB=5.
因为=,
即=,
解得CD=2.4.
故选D.
3.B 设竹子折断处离地面x尺.
根据勾股定理,得x2+32=(10-x)2,
解得x=4.55.
故选B.
4.C
5.C ①因为7不能表示为两个正整数的平方和,
所以7不是广义勾股数,故①结论正确;
②因为13=22+32,
所以13是广义勾股数,故②结论正确;
③两个广义勾股数的和不一定是广义勾股数,如5和10是广义勾股数,但是它们的和不是广义勾股数,故③结论错误;
④设m1=a2+b2,m2=c2+d2,
则m1·m2=(a2+b2)·(c2+d2)
=a2c2+a2d2+b2c2+b2d2
=(a2c2+b2d2+2abcd)+(a2d2+b2c2-2abcd)
=(ac+bd)2+(ad-bc)2,
当a=c,b=d时,ad-bc=0,所以两个广义勾股数的积不一定是广义勾股数,
如:2和2都是广义勾股数,但2×2=4,4不是广义勾股数,故④结论错误.
所以正确的是①②.故选C.
6.x2+(x-6.8)2=102 由门高AB为x尺,则门的宽为(x-6.8)尺,AC=1丈=10尺.
依题意得AB2+BC2=AC2,
即x2+(x-6.8)2=102.
7.北偏东50° 如图.由题意可知AP=12,BP=16,AB=20.
因为AP2+BP2=122+162=202=AB2,
所以△APB是直角三角形,且∠APB=90°.
由题意知∠APN=40°,
所以∠BPN=90°-∠APN=90°-40°=50°.
即乙船沿北偏东50°方向航行.
故答案为北偏东50°.
8.49
9.解:(1)勾股定理的逆定理
(2)由作图方法可知,QR=QC,QS=QC,
所以∠QCR=∠QRC,∠QCS=∠QSC.
因为∠QRC+∠QCS+∠QCR+∠QSC=180°,
所以2(∠QCR+∠QCS)=180°,
所以∠QCR+∠QCS=90°,
即∠RCS=90°.
一、选择题
1.(2021山西)在勾股定理的学习过程中,我们已经学会了运用如图所示的图形,验证著名的勾股定理,这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律,它体现的数学思想是 ( )
A.统计思想 B.分类思想
C.数形结合思想 D.函数思想
2.(2021滨州)在Rt△ABC中,若∠C=90°,AC=3,BC=4,则点C到直线AB的距离为( )
A.3 B.4 C.5 D.2.4
3.(2020巴中)《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何 ”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子 ( )
A.4尺 B.4.55尺 C.5尺 D.5.55尺
4.(2020广西)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意是:如①②(图②为图①的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是 ( )
A.50.5寸 B.52寸 C.101寸 D.104寸
5.(2021常德)阅读理解:如果一个正整数m能表示为两个正整数a,b的平方和,即m=a2+b2,那么称m为广义勾股数,则下面的四个结论:①7不是广义勾股数;②13是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数.依次正确的是 ( )
A.②④ B.①②④ C.①② D.①④
二、填空题
6.(2021岳阳)《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何 ”其意思为:如(示意图),今有一长方形门,高比宽多6尺8寸,门对角线长度恰好为1丈.则门高、宽各是多少(1丈=10尺,1尺=10寸) 设门高AB为x尺,根据题意,可列方程为 .
7.(2021玉林)如图某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里.如果知道甲船沿北偏西40°方向航行,那么乙船沿 方向航行.
8.(2021陕西)我国古代数学家赵爽巧妙地用“弦图”证明了勾股定理,标志着中国古代的数学成就.如图所示的“弦图”是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形.直角三角形的斜边长为13,一条直角边长为12,则小正方形ABCD的面积为 .
三、解答题
9.(2020山西改编)阅读与思考:
下面是小宇同学的数学日记,请仔细阅读,并完成相应的任务.
×年×月×日 星期日
没有直角尺也能作出直角
今天,我在书店一本书上看到下面材料:木工师傅有一块如①所示的四边形木板,他已经在木板上画出一条裁割线AB,现根据木板的情况,要过AB上的一点C,作出AB的垂线,用锯子进行裁割,然而手头没有直角尺,怎么办呢
办法一:如图①,可利用一把有刻度的直尺在AB上量出CD=30 cm,然后分别以D,C为圆心,以50 cm与40 cm为半径画圆弧,两弧相交于点E,作直线CE,则∠DCE必为90°.
办法二:如图②,可以取一根笔直的木棒,用铅笔在木棒上点出M,N两点,然后把木棒斜放在木板上,使点M与点C重合,用铅笔在木板上将点N对应的位置标记
为点Q,保持点N不动,将木棒绕点N旋转,使点M落在AB上,在木板上将点M对应的位置标记为点R.然后将RQ延长,在延长线上截取线段QS=MN,得到点S,作直线SC,则∠RCS=90°.
任务:
(1)填空:“办法一”依据的一个数学定理是 ;
(2)根据“办法二”的操作过程,试说明∠RCS=90°.
答案
勾股定理
1.C
2.D 过点C作CD⊥AB于点D,如图所示.
因为∠ACB=90°,AC=3,BC=4,
所以AB=5.
因为=,
即=,
解得CD=2.4.
故选D.
3.B 设竹子折断处离地面x尺.
根据勾股定理,得x2+32=(10-x)2,
解得x=4.55.
故选B.
4.C
5.C ①因为7不能表示为两个正整数的平方和,
所以7不是广义勾股数,故①结论正确;
②因为13=22+32,
所以13是广义勾股数,故②结论正确;
③两个广义勾股数的和不一定是广义勾股数,如5和10是广义勾股数,但是它们的和不是广义勾股数,故③结论错误;
④设m1=a2+b2,m2=c2+d2,
则m1·m2=(a2+b2)·(c2+d2)
=a2c2+a2d2+b2c2+b2d2
=(a2c2+b2d2+2abcd)+(a2d2+b2c2-2abcd)
=(ac+bd)2+(ad-bc)2,
当a=c,b=d时,ad-bc=0,所以两个广义勾股数的积不一定是广义勾股数,
如:2和2都是广义勾股数,但2×2=4,4不是广义勾股数,故④结论错误.
所以正确的是①②.故选C.
6.x2+(x-6.8)2=102 由门高AB为x尺,则门的宽为(x-6.8)尺,AC=1丈=10尺.
依题意得AB2+BC2=AC2,
即x2+(x-6.8)2=102.
7.北偏东50° 如图.由题意可知AP=12,BP=16,AB=20.
因为AP2+BP2=122+162=202=AB2,
所以△APB是直角三角形,且∠APB=90°.
由题意知∠APN=40°,
所以∠BPN=90°-∠APN=90°-40°=50°.
即乙船沿北偏东50°方向航行.
故答案为北偏东50°.
8.49
9.解:(1)勾股定理的逆定理
(2)由作图方法可知,QR=QC,QS=QC,
所以∠QCR=∠QRC,∠QCS=∠QSC.
因为∠QRC+∠QCS+∠QCR+∠QSC=180°,
所以2(∠QCR+∠QCS)=180°,
所以∠QCR+∠QCS=90°,
即∠RCS=90°.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
