北师大版数学八年级上册同步提优训练:第7章 平行线的证明 中考真题训练(含答案)
文档属性
| 名称 | 北师大版数学八年级上册同步提优训练:第7章 平行线的证明 中考真题训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 243.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览



文档简介
平行线的证明
一、选择题
1.(2021达州)以下命题是假命题的是 ( )
A.的算术平方根是2
B.有两边相等的三角形是等腰三角形
C.一组数据:3,-1,1,1,2,4的中位数是1.5
D.过直线外一点有且只有一条直线与已知直线平行
2.(2021嘉兴)能说明命题“若x为无理数,则x2也是无理数”是假命题的反例是 ( )
A.x=-1 B.x=+1 C.x=3 D.x=-
3.(2021临沂)如图已知AB∥CD,点E在AB上,且∠AEC=40°,CB平分∠DCE,则∠ABC的度数为 ( )
A.10° B.20° C.30° D.40°
4.(2021湖北)如图在△ABC中,∠C=90°,点D在AC上,DE∥AB,若∠CDE=160°,则∠B的度数为 ( )
A.40° B.50° C.60° D.70°
5.(2021齐齐哈尔)一把直尺与一块三角尺如放置,若∠1=47°,则∠2的度数为
( )
A.43° B.47° C.133° D.137°
6.(2021宿迁)如图在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是 ( )
A.30° B.40° C.50° D.60°
7.(2021达州)如图一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=40°时,∠DCN等于 ( )
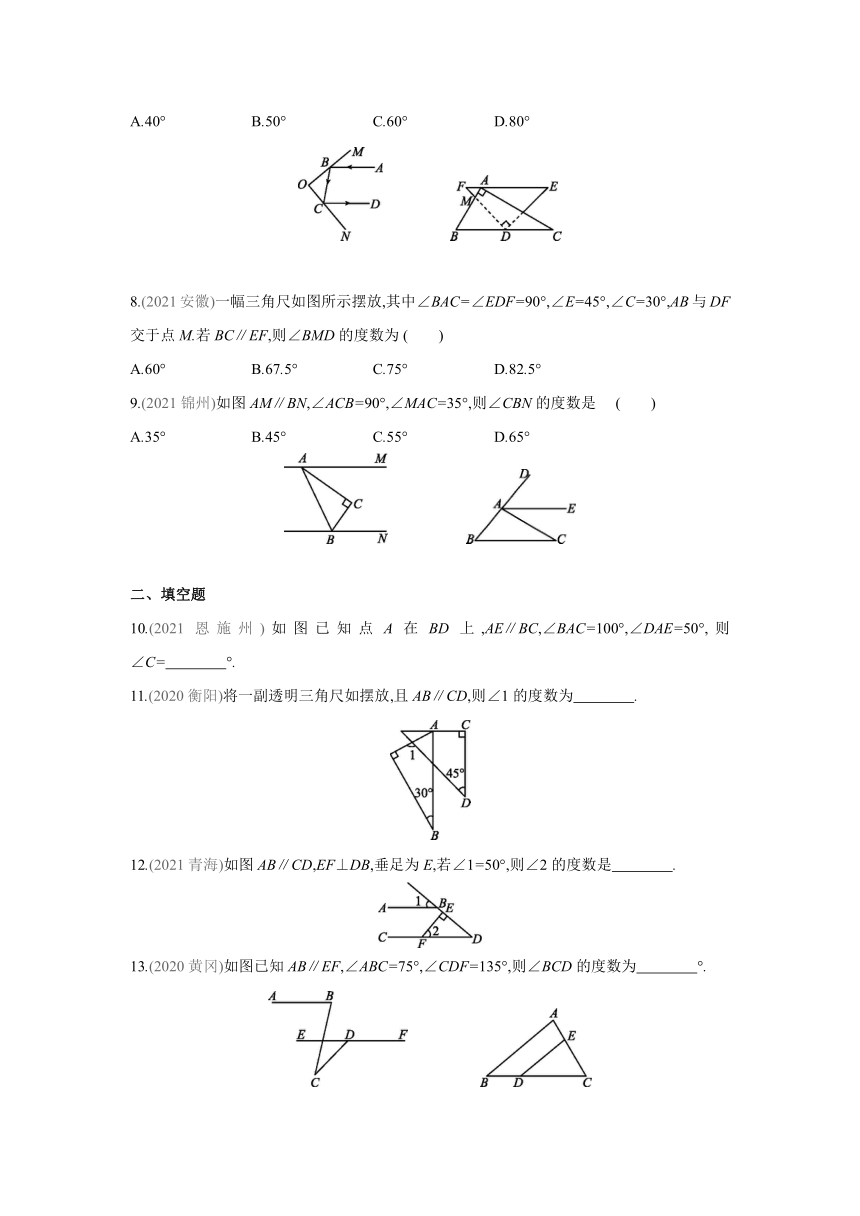
A.40° B.50° C.60° D.80°
8.(2021安徽)一幅三角尺如图所示摆放,其中∠BAC=∠EDF=90°,∠E=45°,∠C=30°,AB与DF交于点M.若BC∥EF,则∠BMD的度数为 ( )
A.60° B.67.5° C.75° D.82.5°
9.(2021锦州)如图AM∥BN,∠ACB=90°,∠MAC=35°,则∠CBN的度数是 ( )
A.35° B.45° C.55° D.65°
二、填空题
10.(2021恩施州)如图已知点A在BD上,AE∥BC,∠BAC=100°,∠DAE=50°,则∠C= °.
11.(2020衡阳)将一副透明三角尺如摆放,且AB∥CD,则∠1的度数为 .
12.(2021青海)如图AB∥CD,EF⊥DB,垂足为E,若∠1=50°,则∠2的度数是 .
13.(2020黄冈)如图已知AB∥EF,∠ABC=75°,∠CDF=135°,则∠BCD的度数为 °.
14.(2021常州)如图在△ABC中,点D,E分别在BC,AC上,∠B=40°,∠C=60°.若DE∥AB,则∠AED= °.
15.(2021河北)如是可调躺椅示意图(数据如图),AE与BD的交点为C,且∠CAB,∠CBA,∠E的度数保持不变.为了舒适,需调整∠D的度数,使∠EFD=110°,则图中∠D应 (填“增加”或“减少”) °.
16.(2021宁夏)已知直线a∥b,把一块含30°角的三角尺按如方式放置,若∠1=43°,则∠2= °.
17.(2020日照)如图有一个含30°角的透明三角尺,一顶点放在直尺的一条边上,若∠2=65°,则∠1的度数是 .
三、解答题
18.(2020宜昌)光线在不同介质中的传播速度不同,从一种介质射向另一种介质时会发生折射.如图水面AB与水杯下沿CD平行,光线EF从水中射向空气时发生折射,光线变成FH,点G在射线EF上,已知∠HFB=20°,∠FED=45°,求∠GFH的度数.
19.(2021武汉)如图AB∥CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F.求证:∠DEF=∠F.
答案
平行线的证明
1.A A项,=2的算术平方根是,原命题是假命题,符合题意;
B项,有两边相等的三角形是等腰三角形,是真命题,不符合题意;
C项,一组数据:3,-1,1,1,2,4的中位数是1.5,原命题是真命题,不符合题意;
D项,过直线外一点有且只有一条直线与已知直线平行,原命题是真命题,不符合题意.
故选A.
2.C
3.B ∵AB∥CD,∠AEC=40°,
∴∠ECD=∠AEC=40°.
∵CB平分∠DCE,
∴∠BCD=∠DCE=20°.
∵AB∥CD,
∴∠ABC=∠BCD=20°.
4.D 5.D
6.B 在△ABC中,∠A=70°,∠C=30°,
∴∠ABC=180°-∠A-∠C=80°.
∵BD平分∠ABC,
∴∠ABD=∠ABC=40°.
∵DE∥AB,
∴∠BDE=∠ABD=40°.
故选B.
7.B ∵∠ABM=40°,∠ABM=∠OBC,
∴∠OBC=40°,
∴∠ABC=180°-∠ABM-∠OBC=180°-40°-40°=100°.
∵CD∥AB,
∴∠ABC+∠BCD=180°,
∴∠BCD=180°-∠ABC=80°.
∵∠BCO=∠DCN,∠BCO+∠BCD+∠DCN=180°,
∴∠DCN=(180°-∠BCD)=50°.
8.C 在△ABC和△DEF中,∠BAC=∠EDF=90°,∠E=45°,∠C=30°,
∴∠B=90°-∠C=60°,∠F=90°-∠E=45°.
∵BC∥EF,
∴∠MDB=∠F=45°.
在△BMD中,∠BMD=180°-∠B-∠MDB=75°.
故选C.
9.C 如图,过点C作CF∥AM.
∵AM∥BN,∴AM∥CF∥BN,
∴∠MAC=∠ACF,∠CBN=∠FCB.
∵∠ACB=90°,∠MAC=35°,
∴∠CBN=∠FCB=∠ACB-∠ACF=∠ACB-∠MAC=90°-35°=55°.
故选C.
10.30 ∵∠BAC+∠CAE+∠DAE=180°,∠BAC=100°,∠DAE=50°,
∴∠CAE=180°-∠BAC-∠DAE=180°-100°-50°=30°.
∵AE∥BC,
∴∠C=∠CAE=30°.
11.105°
12.40° 在△DEF中,∠1=50°,∠DEF=90°,
∴∠D=180°-∠DEF-∠1=40°.
∵AB∥CD,
∴∠2=∠D=40°.
13.30
14.100 在△ABC中,∠A+∠B+∠C=180°.
∵∠B=40°,∠C=60°,
∴∠A=180°-∠B-∠C=180°-40°-60°=80°.
∵DE∥AB,
∴∠A+∠AED=180°,
∴∠AED=180°-80°=100°.
故答案为100.
15.减少 10 延长EF交CD于点G,如图.
∵∠ACB=180°-50°-60°=70°,
∴∠ECD=∠ACB=70°.
∵∠DGF=∠DCE+∠E,
∴∠DGF=70°+30°=100°.
∵∠EFD=110°,∠EFD=∠DGF+∠D,
∴∠D=10°.
而图中∠D=20°,
∴∠D应减少10°.
故答案为减少,10.
16.107 如图所示.
由题意得∠CAB=30°.
∵a∥b,∠1=43°,
∴∠DAB=180°-∠1=137°.
∵∠DAB=∠2+∠CAB,
∴∠2=∠DAB-∠CAB=107°.
故答案为107.
17.25° 如图,延长EF交BC于点G.
∵直尺的上、下两边平行,
即AD∥BC,
∴∠2=∠3=65°.
∴∠1=90°-∠3=90°-65°=25°.
故答案为25°.
18.解:∵AB∥CD,
∴∠GFB=∠FED=45°.
∵∠HFB=20°,
∴∠GFH=∠GFB-∠HFB=45°-20°=25°
19.证明:∵AB∥CD,
∴∠DCF=∠B.
∵∠B=∠D,
∴∠DCF=∠D,
∴AD∥BC,
∴∠DEF=∠F.
一、选择题
1.(2021达州)以下命题是假命题的是 ( )
A.的算术平方根是2
B.有两边相等的三角形是等腰三角形
C.一组数据:3,-1,1,1,2,4的中位数是1.5
D.过直线外一点有且只有一条直线与已知直线平行
2.(2021嘉兴)能说明命题“若x为无理数,则x2也是无理数”是假命题的反例是 ( )
A.x=-1 B.x=+1 C.x=3 D.x=-
3.(2021临沂)如图已知AB∥CD,点E在AB上,且∠AEC=40°,CB平分∠DCE,则∠ABC的度数为 ( )
A.10° B.20° C.30° D.40°
4.(2021湖北)如图在△ABC中,∠C=90°,点D在AC上,DE∥AB,若∠CDE=160°,则∠B的度数为 ( )
A.40° B.50° C.60° D.70°
5.(2021齐齐哈尔)一把直尺与一块三角尺如放置,若∠1=47°,则∠2的度数为
( )
A.43° B.47° C.133° D.137°
6.(2021宿迁)如图在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是 ( )
A.30° B.40° C.50° D.60°
7.(2021达州)如图一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=40°时,∠DCN等于 ( )
A.40° B.50° C.60° D.80°
8.(2021安徽)一幅三角尺如图所示摆放,其中∠BAC=∠EDF=90°,∠E=45°,∠C=30°,AB与DF交于点M.若BC∥EF,则∠BMD的度数为 ( )
A.60° B.67.5° C.75° D.82.5°
9.(2021锦州)如图AM∥BN,∠ACB=90°,∠MAC=35°,则∠CBN的度数是 ( )
A.35° B.45° C.55° D.65°
二、填空题
10.(2021恩施州)如图已知点A在BD上,AE∥BC,∠BAC=100°,∠DAE=50°,则∠C= °.
11.(2020衡阳)将一副透明三角尺如摆放,且AB∥CD,则∠1的度数为 .
12.(2021青海)如图AB∥CD,EF⊥DB,垂足为E,若∠1=50°,则∠2的度数是 .
13.(2020黄冈)如图已知AB∥EF,∠ABC=75°,∠CDF=135°,则∠BCD的度数为 °.
14.(2021常州)如图在△ABC中,点D,E分别在BC,AC上,∠B=40°,∠C=60°.若DE∥AB,则∠AED= °.
15.(2021河北)如是可调躺椅示意图(数据如图),AE与BD的交点为C,且∠CAB,∠CBA,∠E的度数保持不变.为了舒适,需调整∠D的度数,使∠EFD=110°,则图中∠D应 (填“增加”或“减少”) °.
16.(2021宁夏)已知直线a∥b,把一块含30°角的三角尺按如方式放置,若∠1=43°,则∠2= °.
17.(2020日照)如图有一个含30°角的透明三角尺,一顶点放在直尺的一条边上,若∠2=65°,则∠1的度数是 .
三、解答题
18.(2020宜昌)光线在不同介质中的传播速度不同,从一种介质射向另一种介质时会发生折射.如图水面AB与水杯下沿CD平行,光线EF从水中射向空气时发生折射,光线变成FH,点G在射线EF上,已知∠HFB=20°,∠FED=45°,求∠GFH的度数.
19.(2021武汉)如图AB∥CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F.求证:∠DEF=∠F.
答案
平行线的证明
1.A A项,=2的算术平方根是,原命题是假命题,符合题意;
B项,有两边相等的三角形是等腰三角形,是真命题,不符合题意;
C项,一组数据:3,-1,1,1,2,4的中位数是1.5,原命题是真命题,不符合题意;
D项,过直线外一点有且只有一条直线与已知直线平行,原命题是真命题,不符合题意.
故选A.
2.C
3.B ∵AB∥CD,∠AEC=40°,
∴∠ECD=∠AEC=40°.
∵CB平分∠DCE,
∴∠BCD=∠DCE=20°.
∵AB∥CD,
∴∠ABC=∠BCD=20°.
4.D 5.D
6.B 在△ABC中,∠A=70°,∠C=30°,
∴∠ABC=180°-∠A-∠C=80°.
∵BD平分∠ABC,
∴∠ABD=∠ABC=40°.
∵DE∥AB,
∴∠BDE=∠ABD=40°.
故选B.
7.B ∵∠ABM=40°,∠ABM=∠OBC,
∴∠OBC=40°,
∴∠ABC=180°-∠ABM-∠OBC=180°-40°-40°=100°.
∵CD∥AB,
∴∠ABC+∠BCD=180°,
∴∠BCD=180°-∠ABC=80°.
∵∠BCO=∠DCN,∠BCO+∠BCD+∠DCN=180°,
∴∠DCN=(180°-∠BCD)=50°.
8.C 在△ABC和△DEF中,∠BAC=∠EDF=90°,∠E=45°,∠C=30°,
∴∠B=90°-∠C=60°,∠F=90°-∠E=45°.
∵BC∥EF,
∴∠MDB=∠F=45°.
在△BMD中,∠BMD=180°-∠B-∠MDB=75°.
故选C.
9.C 如图,过点C作CF∥AM.
∵AM∥BN,∴AM∥CF∥BN,
∴∠MAC=∠ACF,∠CBN=∠FCB.
∵∠ACB=90°,∠MAC=35°,
∴∠CBN=∠FCB=∠ACB-∠ACF=∠ACB-∠MAC=90°-35°=55°.
故选C.
10.30 ∵∠BAC+∠CAE+∠DAE=180°,∠BAC=100°,∠DAE=50°,
∴∠CAE=180°-∠BAC-∠DAE=180°-100°-50°=30°.
∵AE∥BC,
∴∠C=∠CAE=30°.
11.105°
12.40° 在△DEF中,∠1=50°,∠DEF=90°,
∴∠D=180°-∠DEF-∠1=40°.
∵AB∥CD,
∴∠2=∠D=40°.
13.30
14.100 在△ABC中,∠A+∠B+∠C=180°.
∵∠B=40°,∠C=60°,
∴∠A=180°-∠B-∠C=180°-40°-60°=80°.
∵DE∥AB,
∴∠A+∠AED=180°,
∴∠AED=180°-80°=100°.
故答案为100.
15.减少 10 延长EF交CD于点G,如图.
∵∠ACB=180°-50°-60°=70°,
∴∠ECD=∠ACB=70°.
∵∠DGF=∠DCE+∠E,
∴∠DGF=70°+30°=100°.
∵∠EFD=110°,∠EFD=∠DGF+∠D,
∴∠D=10°.
而图中∠D=20°,
∴∠D应减少10°.
故答案为减少,10.
16.107 如图所示.
由题意得∠CAB=30°.
∵a∥b,∠1=43°,
∴∠DAB=180°-∠1=137°.
∵∠DAB=∠2+∠CAB,
∴∠2=∠DAB-∠CAB=107°.
故答案为107.
17.25° 如图,延长EF交BC于点G.
∵直尺的上、下两边平行,
即AD∥BC,
∴∠2=∠3=65°.
∴∠1=90°-∠3=90°-65°=25°.
故答案为25°.
18.解:∵AB∥CD,
∴∠GFB=∠FED=45°.
∵∠HFB=20°,
∴∠GFH=∠GFB-∠HFB=45°-20°=25°
19.证明:∵AB∥CD,
∴∠DCF=∠B.
∵∠B=∠D,
∴∠DCF=∠D,
∴AD∥BC,
∴∠DEF=∠F.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
