北师大版数学八年级上册 4.1函数 同步提优训练(word版含答案)
文档属性
| 名称 | 北师大版数学八年级上册 4.1函数 同步提优训练(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 150.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 09:57:58 | ||
图片预览

文档简介
1 函数
考向题组训练
命题点 1 判断两个变量是不是函数关系
1.下列两个变量之间不存在函数关系的是 ( )
A.圆的面积S和半径r之间的关系
B.某地一天的温度T与时间t之间的关系
C.某班学生的身高y与这个班学生的学号x之间的关系
D.一个正数b的平方根a与这个正数b之间的关系
2.下列关系式中,y不是x的函数的是 ( )
A.y=±(x>0) B.y=x2
C.y=-(x>0) D.y=()2(x>0)
3.如图所示曲线中不能表示y是x的函数的是 ( )
4.如图线段AB=a,在垂直于AB的射线DE上有一个动点C(点C与点D不重合),分别连接CA,CB,得到△ABC.
(1)指出在△ABC的面积变化的过程中,线段AB,CD的长哪个是常量 哪个是变量
(2)设CD的长为h,△ABC的面积为S,S是不是h的函数
命题点 2 确定自变量的取值范围
5.(2021兴安盟)函数y=(x-)0+中,自变量x的取值范围是 .
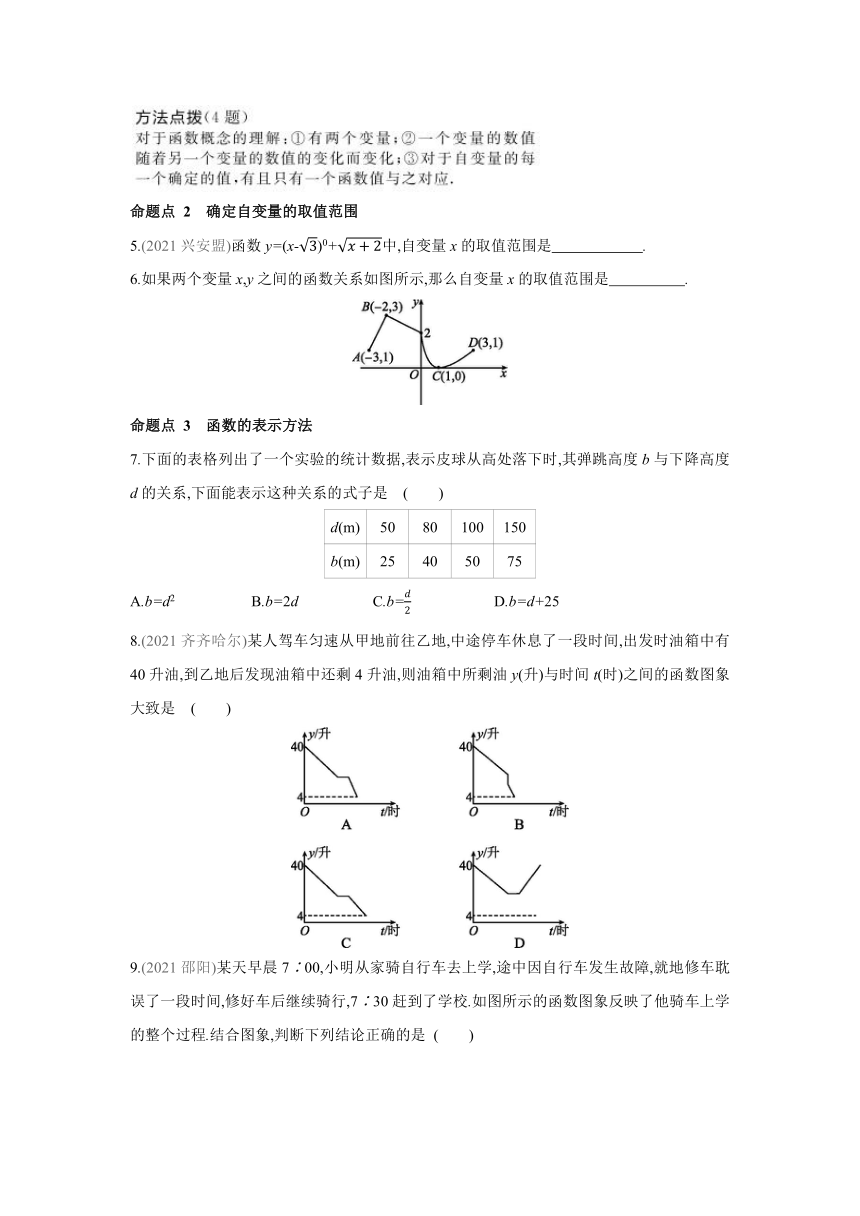
6.如果两个变量x,y之间的函数关系如图所示,那么自变量x的取值范围是 .
命题点 3 函数的表示方法
7.下面的表格列出了一个实验的统计数据,表示皮球从高处落下时,其弹跳高度b与下降高度d的关系,下面能表示这种关系的式子是 ( )
d(m) 50 80 100 150
b(m) 25 40 50 75
A.b=d2 B.b=2d C.b= D.b=d+25
8.(2021齐齐哈尔)某人驾车匀速从甲地前往乙地,中途停车休息了一段时间,出发时油箱中有40升油,到乙地后发现油箱中还剩4升油,则油箱中所剩油y(升)与时间t(时)之间的函数图象大致是 ( )
9.(2021邵阳)某天早晨7∶00,小明从家骑自行车去上学,途中因自行车发生故障,就地修车耽误了一段时间,修好车后继续骑行,7∶30赶到了学校.如图所示的函数图象反映了他骑车上学的整个过程.结合图象,判断下列结论正确的是 ( )
A.小明修车花了15 min
B.小明家距离学校1100 m
C.小明修好车后花了30 min到达学校
D.小明修好车后骑行到学校的平均速度是3 m/s
命题点 4 求函数值
10.在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂重物.下表是测得的弹簧长度y与所挂物体质量x的几组对应值:
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 20 22 24 26 28
(1)上表反映了两个变量 和 之间的关系,其中 是自变量,
是因变量;
(2)不挂重物时,弹簧的长度是 ,所挂重物是3 kg时,弹簧的长度是 ;
(3)试写出y与x之间的关系式(不必写出x的取值范围);
(4)若在弹簧的弹性范围内,弹簧的长度是48 cm,试求出所挂物体的质量是多少千克.
思维拓展培优
11.如图在长方形ABCD中,AB=4,BC=7,P是BC边上与点B不重合的动点,过点P的直线交CD的延长线于点E,交AD于点Q(点Q与点D不重合),且∠EPC=45°.设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系式,并求出自变量x的取值范围.
答案
1 函数
1.D A项,圆的面积S和半径r之间的关系是S=πr2,符合函数的定义;B项,某地一天的温度T与时间t的关系符合函数的定义;C项,每一个学生对应一个身高,故y是x的函数;D项,一个正数b的平方根a与这个正数b之间的关系为a=±,b每取一个正数,a都有两个值与之对应,不符合函数的定义.故选D.
2.A 根据函数的定义易知y=±(x>0)中,一个自变量x对应两个因变量y,故y不是x的函数.
3.C 若y是x的函数,则x取一个值时,y有唯一的一个值与之对应,C选项中的图象,在x轴上取一点(图象与x轴交点除外),即确定一个x的值,这个点都对应图象上的两个点,即一个x值有两个y值与之对应,故此图象不能表示y是x的函数.故选C.
4.解:(1)依题意知,AB的长是常量,CD的长是变量.
(2)S=AB·CD=ah.
因为对于h的每一个确定的值,S都有唯一的值与其对应,
所以S是h的函数.
5.x≥-2且x≠
6.-3≤x≤3 观察可知图象过左边端点A(-3,1)和右边端点D(3,1),
所以自变量的取值范围是-3≤x≤3.
7.C 由统计数据可知:d是b的2倍,
所以b=.
8.C 某人驾车从甲地前往乙地,油量在减小;中途休息时油量不发生变化;再次出发油量继续减小,且油量减小的速度与前面相同;到乙地后发现油箱中还剩油4升.
只有C选项符合要求.
故选C.
9.A A选项,由横坐标可看出,小明修车时间为20-5=15(min),故本选项符合题意;
B选项,由纵坐标看出,小明家离学校的距离为2100 m,故本选项不合题意;
C选项,由横坐标看出,小明修好车后花了30-20=10(min)到达学校,故本选项不合题意;
D选项,小明修好车后骑行到学校的平均速度是(2100-1000)÷10=110(m/min)=(m/s),故本选项不合题意.
故选A.
10. (1)从表格中可看出“弹簧长度”随着“所挂物体质量”的变化而变化,先行变化的是自变量,随之而改变的是因变量;(2)观察表格中的信息即可求解;(3)从表格中可看出弹簧的原长度是18 cm,每增加1 kg 重物,弹簧伸长2 cm,据此写出关系式;(4)将y=48代入关系式即可求解.
解:(1)所挂物体质量 弹簧长度 所挂物体质量
弹簧长度
(2)18 cm 24 cm (3)y=18+2x.
(4)当y=48时,18+2x=48,解得x=15,因此所挂物体的质量是15 kg.
11.解:如图,过点D作DF∥PQ交BC于点F,则∠DFC=∠EPC=45°,
所以FC=CD=4.
所以BF=3.
因为点Q与点D不重合,点E在CD的延长线上,
所以BP<3.
因为BP=x,
所以PC=7-x.
在Rt△PCE中,∠C=90°,∠EPC=45°,
所以CE=PC=7-x.
所以QD=ED=CE-CD=3-x.
所以AQ=AD-QD=7-(3-x)=4+x.
所以y=(BP+AQ)·AB=(x+4+x)×4=4x+8(0
考向题组训练
命题点 1 判断两个变量是不是函数关系
1.下列两个变量之间不存在函数关系的是 ( )
A.圆的面积S和半径r之间的关系
B.某地一天的温度T与时间t之间的关系
C.某班学生的身高y与这个班学生的学号x之间的关系
D.一个正数b的平方根a与这个正数b之间的关系
2.下列关系式中,y不是x的函数的是 ( )
A.y=±(x>0) B.y=x2
C.y=-(x>0) D.y=()2(x>0)
3.如图所示曲线中不能表示y是x的函数的是 ( )
4.如图线段AB=a,在垂直于AB的射线DE上有一个动点C(点C与点D不重合),分别连接CA,CB,得到△ABC.
(1)指出在△ABC的面积变化的过程中,线段AB,CD的长哪个是常量 哪个是变量
(2)设CD的长为h,△ABC的面积为S,S是不是h的函数
命题点 2 确定自变量的取值范围
5.(2021兴安盟)函数y=(x-)0+中,自变量x的取值范围是 .
6.如果两个变量x,y之间的函数关系如图所示,那么自变量x的取值范围是 .
命题点 3 函数的表示方法
7.下面的表格列出了一个实验的统计数据,表示皮球从高处落下时,其弹跳高度b与下降高度d的关系,下面能表示这种关系的式子是 ( )
d(m) 50 80 100 150
b(m) 25 40 50 75
A.b=d2 B.b=2d C.b= D.b=d+25
8.(2021齐齐哈尔)某人驾车匀速从甲地前往乙地,中途停车休息了一段时间,出发时油箱中有40升油,到乙地后发现油箱中还剩4升油,则油箱中所剩油y(升)与时间t(时)之间的函数图象大致是 ( )
9.(2021邵阳)某天早晨7∶00,小明从家骑自行车去上学,途中因自行车发生故障,就地修车耽误了一段时间,修好车后继续骑行,7∶30赶到了学校.如图所示的函数图象反映了他骑车上学的整个过程.结合图象,判断下列结论正确的是 ( )
A.小明修车花了15 min
B.小明家距离学校1100 m
C.小明修好车后花了30 min到达学校
D.小明修好车后骑行到学校的平均速度是3 m/s
命题点 4 求函数值
10.在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂重物.下表是测得的弹簧长度y与所挂物体质量x的几组对应值:
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 20 22 24 26 28
(1)上表反映了两个变量 和 之间的关系,其中 是自变量,
是因变量;
(2)不挂重物时,弹簧的长度是 ,所挂重物是3 kg时,弹簧的长度是 ;
(3)试写出y与x之间的关系式(不必写出x的取值范围);
(4)若在弹簧的弹性范围内,弹簧的长度是48 cm,试求出所挂物体的质量是多少千克.
思维拓展培优
11.如图在长方形ABCD中,AB=4,BC=7,P是BC边上与点B不重合的动点,过点P的直线交CD的延长线于点E,交AD于点Q(点Q与点D不重合),且∠EPC=45°.设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系式,并求出自变量x的取值范围.
答案
1 函数
1.D A项,圆的面积S和半径r之间的关系是S=πr2,符合函数的定义;B项,某地一天的温度T与时间t的关系符合函数的定义;C项,每一个学生对应一个身高,故y是x的函数;D项,一个正数b的平方根a与这个正数b之间的关系为a=±,b每取一个正数,a都有两个值与之对应,不符合函数的定义.故选D.
2.A 根据函数的定义易知y=±(x>0)中,一个自变量x对应两个因变量y,故y不是x的函数.
3.C 若y是x的函数,则x取一个值时,y有唯一的一个值与之对应,C选项中的图象,在x轴上取一点(图象与x轴交点除外),即确定一个x的值,这个点都对应图象上的两个点,即一个x值有两个y值与之对应,故此图象不能表示y是x的函数.故选C.
4.解:(1)依题意知,AB的长是常量,CD的长是变量.
(2)S=AB·CD=ah.
因为对于h的每一个确定的值,S都有唯一的值与其对应,
所以S是h的函数.
5.x≥-2且x≠
6.-3≤x≤3 观察可知图象过左边端点A(-3,1)和右边端点D(3,1),
所以自变量的取值范围是-3≤x≤3.
7.C 由统计数据可知:d是b的2倍,
所以b=.
8.C 某人驾车从甲地前往乙地,油量在减小;中途休息时油量不发生变化;再次出发油量继续减小,且油量减小的速度与前面相同;到乙地后发现油箱中还剩油4升.
只有C选项符合要求.
故选C.
9.A A选项,由横坐标可看出,小明修车时间为20-5=15(min),故本选项符合题意;
B选项,由纵坐标看出,小明家离学校的距离为2100 m,故本选项不合题意;
C选项,由横坐标看出,小明修好车后花了30-20=10(min)到达学校,故本选项不合题意;
D选项,小明修好车后骑行到学校的平均速度是(2100-1000)÷10=110(m/min)=(m/s),故本选项不合题意.
故选A.
10. (1)从表格中可看出“弹簧长度”随着“所挂物体质量”的变化而变化,先行变化的是自变量,随之而改变的是因变量;(2)观察表格中的信息即可求解;(3)从表格中可看出弹簧的原长度是18 cm,每增加1 kg 重物,弹簧伸长2 cm,据此写出关系式;(4)将y=48代入关系式即可求解.
解:(1)所挂物体质量 弹簧长度 所挂物体质量
弹簧长度
(2)18 cm 24 cm (3)y=18+2x.
(4)当y=48时,18+2x=48,解得x=15,因此所挂物体的质量是15 kg.
11.解:如图,过点D作DF∥PQ交BC于点F,则∠DFC=∠EPC=45°,
所以FC=CD=4.
所以BF=3.
因为点Q与点D不重合,点E在CD的延长线上,
所以BP<3.
因为BP=x,
所以PC=7-x.
在Rt△PCE中,∠C=90°,∠EPC=45°,
所以CE=PC=7-x.
所以QD=ED=CE-CD=3-x.
所以AQ=AD-QD=7-(3-x)=4+x.
所以y=(BP+AQ)·AB=(x+4+x)×4=4x+8(0
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
