沪科版八年级数学上册 13.2 命题与证明(第5课时) 教案
文档属性
| 名称 | 沪科版八年级数学上册 13.2 命题与证明(第5课时) 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 728.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览



文档简介
第13章 三角形中的边角关系、命题与证明
13.2 命题与证明
第5课时 三角形的外角
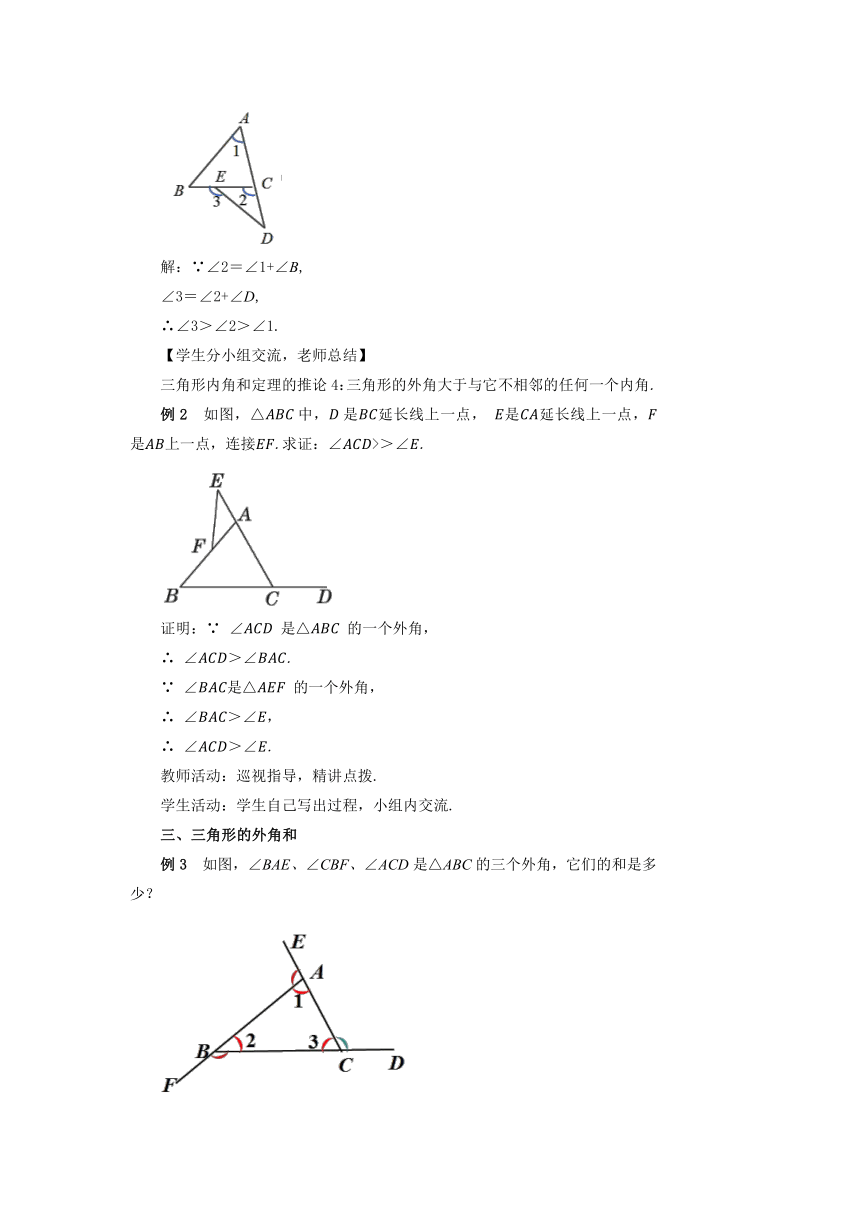
教学目标 1.引导学生理解三角形的外角的概念. 2.使学生掌握三角形外角的性质. 3.让学生灵活运用三角形内角和定理及外角的性质解决相关问题. 教学重难点 重点:三角形外角的性质. 难点:运用三角形内角和定理及外角的性质解决相关问题.. 教学过程 导入新课 三角形的内角和等于180°. 如图,在△中,∠=45°,∠==80°,则∠==55°. 如果我们将延长至点,则可以得到一个新角∠ 思考: ∠还是△的内角吗? 【学生讨论,老师引出新课】 探究新知 一、三角形的外角的概念 如图,把△ABC的一边BC延长,得到∠ACD,像这样,由三角形的一边与另一边的延长线组成的角,叫做三角形的外角. ∠ACD是△ABC的一个外角. 二、三角形的外角的性质 问题1 :如图,△ABC的外角∠BCD与其相邻的内角∠ACB有什么关系? 【学生讨论,老师总结】 ∠BCD与∠ACB互补. 问题2:如图,△ABC的外角∠BCD与其不相邻的两内角(∠A、∠B)有什么关系? 【学生讨论,老师总结】 ∠A+∠B=∠BCD 问题2:你会证明这个结论吗? 已知:如图,△ABC,求证:∠ACD=∠A+∠B. 证明:过C作CE∥AB, ∴∠1= ∠B, (两直线平行,同位角相等) ∠2= ∠A , (两直线平行,内错角相等) ∴∠ACD= ∠1+ ∠2= ∠A+ ∠B. 【老师总结】三角形内角和定理的推论3: 三角形的外角等于与它不相邻的两个内角的和. 应用格式: ∵ ∠ACD是△ABC的一个外角, ∴ ∠ACD=∠A+∠B. 例1 一个零件的形状如图所示,按规定∠ 应等于90°,∠,∠ 应分别是21°和32°,检验工人量得∠,就断定这个零件不合格,这是为什么呢? 解:如图所示,延长交 于点. 因为∠是△ 的一个外角, 所以∠=∠+∠. 又因为∠ 是△ 的一个外角, 所以∠=∠+∠. 所以∠=∠+∠+∠=90°+21°+32°= 143°≠148°. 所以可以断定这个零件不合格. 教师活动:巡视指导,精讲点拨. 学生活动:学生自己写出过程,小组内交流. 探究1: 如图 ,试比较∠2 、∠1的大小. 解:∵ ∠2=∠1+∠B, ∴ ∠2>∠1. 探究2: 如图,试比较∠3 、∠2、 ∠1的大小. 解:∵∠2=∠1+∠B, ∠3=∠2+∠D, ∴∠3>∠2>∠1. 【学生分小组交流,老师总结】 三角形内角和定理的推论4:三角形的外角大于与它不相邻的任何一个内角. 例2 如图,△中,是延长线上一点, 是延长线上一点,是上一点,连接.求证:∠>>∠. 证明:∵ ∠ 是△ 的一个外角, ∴ ∠>∠. ∵ ∠是△ 的一个外角, ∴ ∠>∠, ∴ ∠>∠. 教师活动:巡视指导,精讲点拨. 学生活动:学生自己写出过程,小组内交流. 三、三角形的外角和 例3 如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角,它们的和是多少? 解:由三角形的一个外角等于与它不相邻的两个内角的和,得 ∠BAE=∠2+∠3, ∠CBF=∠1+∠3, ∠ACD=∠1+∠2. 又知∠1+∠2+∠3=180 °, 所以∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3)=360 °. 你还有其他解法吗? 【学生分组交流讨论】 解法2:如图,∠BAE+∠1=180°, ① ∠CBF+∠2=180°,② ∠ACD+∠3=180°.③ 又知∠1+∠2+∠3=180°, ①+ ②+ ③得 ∠BAE+∠CBF+∠ACD+(∠1+∠2+∠3)=540 °, 所以∠BAE+∠CBF+∠ACD=540°-180°=360°. 解法3 :如图所示,过点作射线,使∥. ∵ ∥, ∴ ∠ =∠,∠ =∠. ∴ ∠+∠+∠ =∠+∠+∠. 结论:三角形的外角和等于360°. 课堂练习 1.已知△的一个外角为50°,则△ABC一定是( ) A.锐角三角形 B.钝角三角形 C.直角三角形 D.钝角三角形或锐角三角形 2.如图,AB∥CD,∠A=37°, ∠C=63°,那么∠F 等于( ) A.26° B.28° C.30° D.32° 3.将一副直角三角尺如图所示放置,使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边在同一条直线上, 则∠1 的度数为( ) A.75° B.65° C.45° D.30° 4.如图,在△中,∠,点延长线上一点,∠,则∠= . 5.如图,P为△ABC内一点,∠BPC=150°,∠ABP=20°,∠ACP=30°, 求∠A的度数. 6.如图,求∠A+∠B+∠C+∠D+∠E的度数. 参考答案 1.B 2.A 3. A 4.70° 5. 解:延长BP交AC于点E, 则∠BPC、∠PEC分别为△PCE、△ABE的外角, ∴∠BPC=∠PEC+∠PCE, ∠PEC=∠ABE+∠A, ∴∠PEC=∠BPC-∠PCE=150°-30°=120°. ∴∠A=∠PEC-∠ABE=120°-20°=100°. 6.解:如图,∵ ∠1是△FBE的外角, ∴∠1=∠B+ ∠E, 同理∠2=∠A+∠D. 在△CFG中,∠C+∠1+∠2=180 , ∴ ∠A+∠B+∠C+∠D+∠E= 180 . 课堂小结 布置作业 P83练习 板书设计 三角形的外角 1.三角形外角的概念 2.三角形外角的性质 推论3:三角形的外角等于与它不相邻的两个内角的和 推论4:三角形的外角大于与它不相邻的任何一个内角 3.三角形的外角和等于360°
13.2 命题与证明
第5课时 三角形的外角
教学目标 1.引导学生理解三角形的外角的概念. 2.使学生掌握三角形外角的性质. 3.让学生灵活运用三角形内角和定理及外角的性质解决相关问题. 教学重难点 重点:三角形外角的性质. 难点:运用三角形内角和定理及外角的性质解决相关问题.. 教学过程 导入新课 三角形的内角和等于180°. 如图,在△中,∠=45°,∠==80°,则∠==55°. 如果我们将延长至点,则可以得到一个新角∠ 思考: ∠还是△的内角吗? 【学生讨论,老师引出新课】 探究新知 一、三角形的外角的概念 如图,把△ABC的一边BC延长,得到∠ACD,像这样,由三角形的一边与另一边的延长线组成的角,叫做三角形的外角. ∠ACD是△ABC的一个外角. 二、三角形的外角的性质 问题1 :如图,△ABC的外角∠BCD与其相邻的内角∠ACB有什么关系? 【学生讨论,老师总结】 ∠BCD与∠ACB互补. 问题2:如图,△ABC的外角∠BCD与其不相邻的两内角(∠A、∠B)有什么关系? 【学生讨论,老师总结】 ∠A+∠B=∠BCD 问题2:你会证明这个结论吗? 已知:如图,△ABC,求证:∠ACD=∠A+∠B. 证明:过C作CE∥AB, ∴∠1= ∠B, (两直线平行,同位角相等) ∠2= ∠A , (两直线平行,内错角相等) ∴∠ACD= ∠1+ ∠2= ∠A+ ∠B. 【老师总结】三角形内角和定理的推论3: 三角形的外角等于与它不相邻的两个内角的和. 应用格式: ∵ ∠ACD是△ABC的一个外角, ∴ ∠ACD=∠A+∠B. 例1 一个零件的形状如图所示,按规定∠ 应等于90°,∠,∠ 应分别是21°和32°,检验工人量得∠,就断定这个零件不合格,这是为什么呢? 解:如图所示,延长交 于点. 因为∠是△ 的一个外角, 所以∠=∠+∠. 又因为∠ 是△ 的一个外角, 所以∠=∠+∠. 所以∠=∠+∠+∠=90°+21°+32°= 143°≠148°. 所以可以断定这个零件不合格. 教师活动:巡视指导,精讲点拨. 学生活动:学生自己写出过程,小组内交流. 探究1: 如图 ,试比较∠2 、∠1的大小. 解:∵ ∠2=∠1+∠B, ∴ ∠2>∠1. 探究2: 如图,试比较∠3 、∠2、 ∠1的大小. 解:∵∠2=∠1+∠B, ∠3=∠2+∠D, ∴∠3>∠2>∠1. 【学生分小组交流,老师总结】 三角形内角和定理的推论4:三角形的外角大于与它不相邻的任何一个内角. 例2 如图,△中,是延长线上一点, 是延长线上一点,是上一点,连接.求证:∠>>∠. 证明:∵ ∠ 是△ 的一个外角, ∴ ∠>∠. ∵ ∠是△ 的一个外角, ∴ ∠>∠, ∴ ∠>∠. 教师活动:巡视指导,精讲点拨. 学生活动:学生自己写出过程,小组内交流. 三、三角形的外角和 例3 如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角,它们的和是多少? 解:由三角形的一个外角等于与它不相邻的两个内角的和,得 ∠BAE=∠2+∠3, ∠CBF=∠1+∠3, ∠ACD=∠1+∠2. 又知∠1+∠2+∠3=180 °, 所以∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3)=360 °. 你还有其他解法吗? 【学生分组交流讨论】 解法2:如图,∠BAE+∠1=180°, ① ∠CBF+∠2=180°,② ∠ACD+∠3=180°.③ 又知∠1+∠2+∠3=180°, ①+ ②+ ③得 ∠BAE+∠CBF+∠ACD+(∠1+∠2+∠3)=540 °, 所以∠BAE+∠CBF+∠ACD=540°-180°=360°. 解法3 :如图所示,过点作射线,使∥. ∵ ∥, ∴ ∠ =∠,∠ =∠. ∴ ∠+∠+∠ =∠+∠+∠. 结论:三角形的外角和等于360°. 课堂练习 1.已知△的一个外角为50°,则△ABC一定是( ) A.锐角三角形 B.钝角三角形 C.直角三角形 D.钝角三角形或锐角三角形 2.如图,AB∥CD,∠A=37°, ∠C=63°,那么∠F 等于( ) A.26° B.28° C.30° D.32° 3.将一副直角三角尺如图所示放置,使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边在同一条直线上, 则∠1 的度数为( ) A.75° B.65° C.45° D.30° 4.如图,在△中,∠,点延长线上一点,∠,则∠= . 5.如图,P为△ABC内一点,∠BPC=150°,∠ABP=20°,∠ACP=30°, 求∠A的度数. 6.如图,求∠A+∠B+∠C+∠D+∠E的度数. 参考答案 1.B 2.A 3. A 4.70° 5. 解:延长BP交AC于点E, 则∠BPC、∠PEC分别为△PCE、△ABE的外角, ∴∠BPC=∠PEC+∠PCE, ∠PEC=∠ABE+∠A, ∴∠PEC=∠BPC-∠PCE=150°-30°=120°. ∴∠A=∠PEC-∠ABE=120°-20°=100°. 6.解:如图,∵ ∠1是△FBE的外角, ∴∠1=∠B+ ∠E, 同理∠2=∠A+∠D. 在△CFG中,∠C+∠1+∠2=180 , ∴ ∠A+∠B+∠C+∠D+∠E= 180 . 课堂小结 布置作业 P83练习 板书设计 三角形的外角 1.三角形外角的概念 2.三角形外角的性质 推论3:三角形的外角等于与它不相邻的两个内角的和 推论4:三角形的外角大于与它不相邻的任何一个内角 3.三角形的外角和等于360°
