沪科版八年级上册11.1平面直角坐标系中的图形(第2课时) 课件(共20张PPT)
文档属性
| 名称 | 沪科版八年级上册11.1平面直角坐标系中的图形(第2课时) 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 919.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
第11章 平面直角坐标系
11.1 平面内点的坐标
第2课时 平面直角坐标系中的图形
学 习 目 标
1
2
进一步理解平面直角坐标系中点的坐标特点.
能够有坐标确定平面直角坐标系中的几何图形.
并能借助平面直角坐标系求图形的面积.(重点)
3
进一步体会数形结合的思想在解决问题中的应用.(难点)
1.什么是平面直角坐标系?
2.坐标轴分平面为几个部分,每一部分内点的坐标有什么特点?
3.如何求平面内点的坐标?
复习巩固
y
5
-5
-2
-3
-4
-1
2
4
3
1
-6
6
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
X
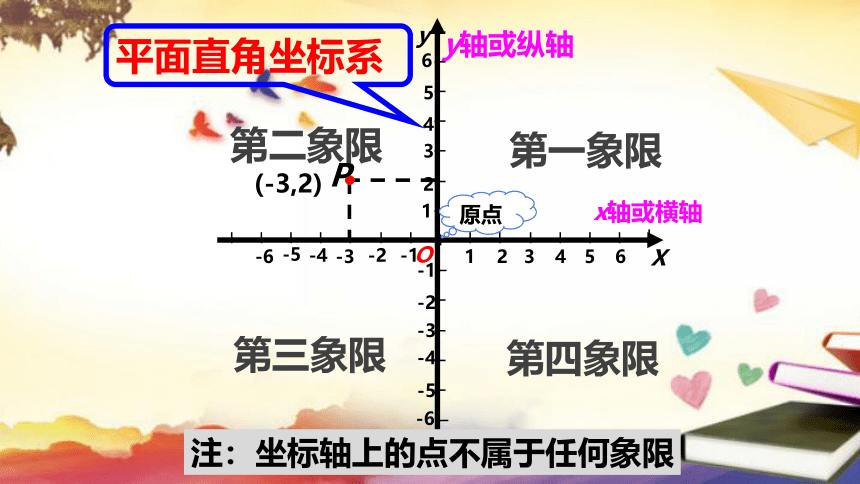
x轴或横轴
y轴或纵轴
平面直角坐标系
第一象限
第二象限
第三象限
第四象限
P
(-3,2)
原点
注:坐标轴上的点不属于任何象限
O
★ 4、坐标轴上的点坐标特点:
原点的坐标为(0,0).
x轴上的点的纵坐标为0,
表示为(x,0);
y轴上点的横坐标为0,
表示为(0,y).
5、考考你:请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5,2) , B(3,-2),C(0,4),D(-6,0),E(1,8),F(0,0),G(5,0),H(-6,-4),K(0,-3)
解:A在第二象限,
B在第四象限,
C在y轴的正半轴,
D在x轴的负半轴,
E在第一象限,
F在原点,
H在第三象限,
G在x轴的正半轴,
K在y轴的负半轴.
1
1
-1
-2
-3
-4
2
3
2
3
4
4
-1
-2
-3
-4
x
y
O
A
E
C
B
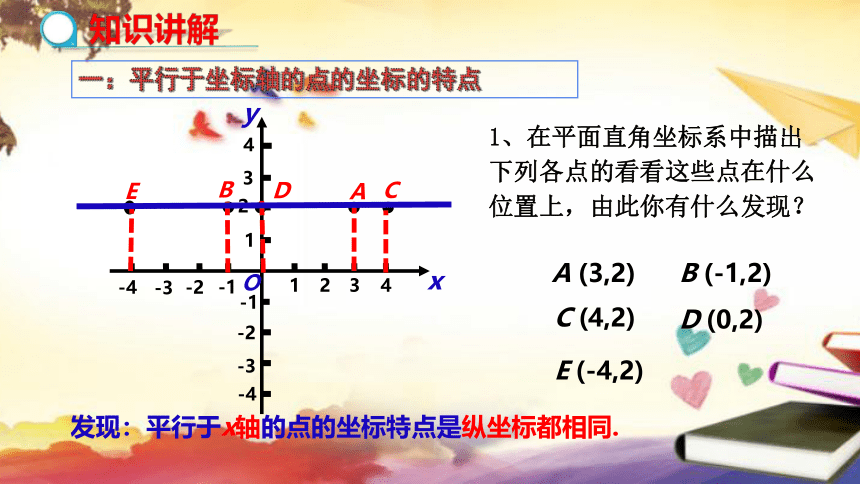
1、在平面直角坐标系中描出下列各点的看看这些点在什么位置上,由此你有什么发现?
A (3,2)
B (-1,2)
C (4,2)
D (0,2)
E (-4,2)
D
发现:平行于x轴的点的坐标特点是纵坐标都相同.
知识讲解
一:平行于坐标轴的点的坐标的特点
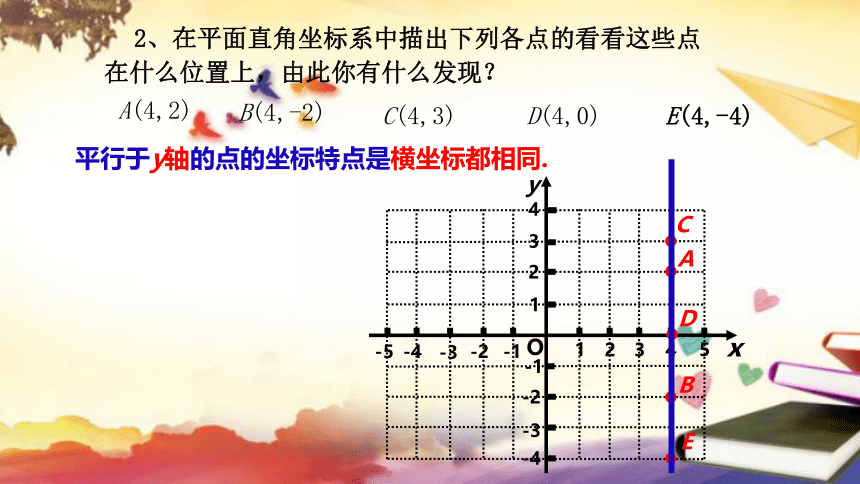
2、在平面直角坐标系中描出下列各点的看看这些点在什么位置上,由此你有什么发现?
A(4,2)
B(4,-2)
C(4,3)
D(4,0)
E(4,-4)
-4
-5
x
y
1
1
-1
-2
-3
2
3
2
3
4
5
4
-1
-2
-3
-4
O
A
B
C
D
E
平行于y轴的点的坐标特点是横坐标都相同.
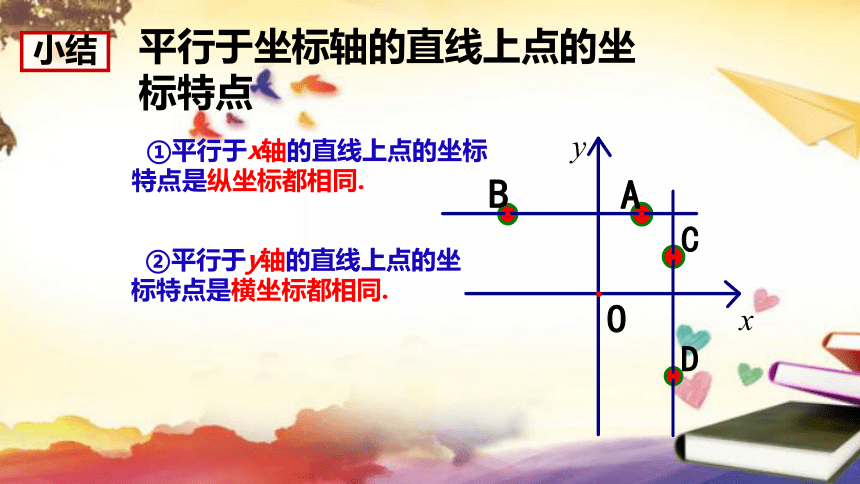
小结
平行于坐标轴的直线上点的坐标特点
①平行于x轴的直线上点的坐标特点是纵坐标都相同.
x
y
②平行于y轴的直线上点的坐标特点是横坐标都相同.
1、已知点A(m+1,-2) , B(3,m-1).
①若直线AB∥ x轴,则m的值为 ;
②若直线AB∥ y轴,则m的值为 ;
1
2
跟踪训练
二:平面直角坐标系中的几何图形
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
x
y
O
A
B
C
D
例1.(1)如图,在平面直角坐标系中描绘出下列各点:
(2)按次序A→B →C →D →A将所描绘出的点用线段连接起来,看看得到的是什么图形?
解:(2)按次序A→B →C →D →A将所描的点用线段连接,得到的是四边形.
A(2,0),B(1,3),C(-2,-2) ,D(1,-2).
(3)计算所得到的面积图形.
(3)计算所得到的面积图形.
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
x
y
O
A
B
C
D
- ×5×3
1
2
方法1:
5×4
- ×1×2
1
2
- ×1×2
1
2
=
3
2
-1
20- -
15
2
=10
(3)计算所得到的面积图形.
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
x
y
O
A
B
C
D
方法2:S四边形ABCD
=S△BCD
+S△ABD
=
×3×5
1
2
+ ×5×1
1
2
=
15
2
+
5
2
=10
1.在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来得到一个封闭图形,说说你得到的是什么图形,并计算它们的面积.
1
1
-1
-2
-3
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
x
y
O
A(-1,2) , B(-2,-1) , C(2,-1) , D(3,2)
A
B
C
D
解:得到的是一个平行四边形,
它的面积是
4×3
=6.
随堂训练
2、(1)如果我们取x轴正半轴上的点为起始点,按逆时针顺序,你能说出这个图形是由那些点顺次连接成的吗?
(2)在一位同学看不见下图的情况下,你如何向他描述,让他能画出这个图.
(6,0)
(4,2)
(4,4)
(2,4)
(0,6)
(-2,4)
(-4,4)
(-4,2)
(0,-6)
(-4,-2)
(-4,-4)
(-2,-4)
(0,-6)
(2,-4)
(4,-4)
(4,-2)
解:(2)在平面直角坐标系中,先描出点
(6,0),(4,2),(4,4),(2,4),(0,6),
(-2,4),(-4,4),(-4,2),(0,-6),
(-4,-2),(-4,-4),(-2,-4),(0,-6),
(2,-4),(4,-4),(4,-2),
然后把它们顺次连接成一个封闭的图形.
B
3.如图,在平面直角坐标系中,梯形ABCD四个顶点的坐标分别为A(- 2,3),B(- 3,0),C(4,0),D(2,3),则梯形ABCD的面积为( )
A.33 B.16.5 C.20 D.40
B
4.如图,求S△ABC的解法正确的是( )
① ×|AC|×|BO|;② ×|AO|×|OB|十 ×|OC|×OB| ;
③ ×|AB|×|AC|
A.①②③ B.①② C.①③ D.②③
5、已知A(3,2),AB∥y轴,且AB=4.写出B点的坐标。
解:
设B点坐标为()
根据题意可得
又因为AB=4
所以|b-2|=4
解得b=6或-2
所以B点的坐标为(3,6)或(3,-2).
1、平行于x轴或y轴的点的坐标特点,
2、计算封闭图形的面积;
3、在平面直角坐标系中描述一个图形的方法.
课堂小结
第11章 平面直角坐标系
11.1 平面内点的坐标
第2课时 平面直角坐标系中的图形
学 习 目 标
1
2
进一步理解平面直角坐标系中点的坐标特点.
能够有坐标确定平面直角坐标系中的几何图形.
并能借助平面直角坐标系求图形的面积.(重点)
3
进一步体会数形结合的思想在解决问题中的应用.(难点)
1.什么是平面直角坐标系?
2.坐标轴分平面为几个部分,每一部分内点的坐标有什么特点?
3.如何求平面内点的坐标?
复习巩固
y
5
-5
-2
-3
-4
-1
2
4
3
1
-6
6
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
X
x轴或横轴
y轴或纵轴
平面直角坐标系
第一象限
第二象限
第三象限
第四象限
P
(-3,2)
原点
注:坐标轴上的点不属于任何象限
O
★ 4、坐标轴上的点坐标特点:
原点的坐标为(0,0).
x轴上的点的纵坐标为0,
表示为(x,0);
y轴上点的横坐标为0,
表示为(0,y).
5、考考你:请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5,2) , B(3,-2),C(0,4),D(-6,0),E(1,8),F(0,0),G(5,0),H(-6,-4),K(0,-3)
解:A在第二象限,
B在第四象限,
C在y轴的正半轴,
D在x轴的负半轴,
E在第一象限,
F在原点,
H在第三象限,
G在x轴的正半轴,
K在y轴的负半轴.
1
1
-1
-2
-3
-4
2
3
2
3
4
4
-1
-2
-3
-4
x
y
O
A
E
C
B
1、在平面直角坐标系中描出下列各点的看看这些点在什么位置上,由此你有什么发现?
A (3,2)
B (-1,2)
C (4,2)
D (0,2)
E (-4,2)
D
发现:平行于x轴的点的坐标特点是纵坐标都相同.
知识讲解
一:平行于坐标轴的点的坐标的特点
2、在平面直角坐标系中描出下列各点的看看这些点在什么位置上,由此你有什么发现?
A(4,2)
B(4,-2)
C(4,3)
D(4,0)
E(4,-4)
-4
-5
x
y
1
1
-1
-2
-3
2
3
2
3
4
5
4
-1
-2
-3
-4
O
A
B
C
D
E
平行于y轴的点的坐标特点是横坐标都相同.
小结
平行于坐标轴的直线上点的坐标特点
①平行于x轴的直线上点的坐标特点是纵坐标都相同.
x
y
②平行于y轴的直线上点的坐标特点是横坐标都相同.
1、已知点A(m+1,-2) , B(3,m-1).
①若直线AB∥ x轴,则m的值为 ;
②若直线AB∥ y轴,则m的值为 ;
1
2
跟踪训练
二:平面直角坐标系中的几何图形
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
x
y
O
A
B
C
D
例1.(1)如图,在平面直角坐标系中描绘出下列各点:
(2)按次序A→B →C →D →A将所描绘出的点用线段连接起来,看看得到的是什么图形?
解:(2)按次序A→B →C →D →A将所描的点用线段连接,得到的是四边形.
A(2,0),B(1,3),C(-2,-2) ,D(1,-2).
(3)计算所得到的面积图形.
(3)计算所得到的面积图形.
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
x
y
O
A
B
C
D
- ×5×3
1
2
方法1:
5×4
- ×1×2
1
2
- ×1×2
1
2
=
3
2
-1
20- -
15
2
=10
(3)计算所得到的面积图形.
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
x
y
O
A
B
C
D
方法2:S四边形ABCD
=S△BCD
+S△ABD
=
×3×5
1
2
+ ×5×1
1
2
=
15
2
+
5
2
=10
1.在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来得到一个封闭图形,说说你得到的是什么图形,并计算它们的面积.
1
1
-1
-2
-3
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
x
y
O
A(-1,2) , B(-2,-1) , C(2,-1) , D(3,2)
A
B
C
D
解:得到的是一个平行四边形,
它的面积是
4×3
=6.
随堂训练
2、(1)如果我们取x轴正半轴上的点为起始点,按逆时针顺序,你能说出这个图形是由那些点顺次连接成的吗?
(2)在一位同学看不见下图的情况下,你如何向他描述,让他能画出这个图.
(6,0)
(4,2)
(4,4)
(2,4)
(0,6)
(-2,4)
(-4,4)
(-4,2)
(0,-6)
(-4,-2)
(-4,-4)
(-2,-4)
(0,-6)
(2,-4)
(4,-4)
(4,-2)
解:(2)在平面直角坐标系中,先描出点
(6,0),(4,2),(4,4),(2,4),(0,6),
(-2,4),(-4,4),(-4,2),(0,-6),
(-4,-2),(-4,-4),(-2,-4),(0,-6),
(2,-4),(4,-4),(4,-2),
然后把它们顺次连接成一个封闭的图形.
B
3.如图,在平面直角坐标系中,梯形ABCD四个顶点的坐标分别为A(- 2,3),B(- 3,0),C(4,0),D(2,3),则梯形ABCD的面积为( )
A.33 B.16.5 C.20 D.40
B
4.如图,求S△ABC的解法正确的是( )
① ×|AC|×|BO|;② ×|AO|×|OB|十 ×|OC|×OB| ;
③ ×|AB|×|AC|
A.①②③ B.①② C.①③ D.②③
5、已知A(3,2),AB∥y轴,且AB=4.写出B点的坐标。
解:
设B点坐标为()
根据题意可得
又因为AB=4
所以|b-2|=4
解得b=6或-2
所以B点的坐标为(3,6)或(3,-2).
1、平行于x轴或y轴的点的坐标特点,
2、计算封闭图形的面积;
3、在平面直角坐标系中描述一个图形的方法.
课堂小结
