2021-2022学年湘教版数学八年级上册 1.1.1分式的概念 课件(共14张PPT)
文档属性
| 名称 | 2021-2022学年湘教版数学八年级上册 1.1.1分式的概念 课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 544.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第一章 分式
第1课时 分式的概念
导入新课
想一想:下列式子中哪些是整式?
② ③ ④
⑤ ⑥ ⑦ ⑧
√
√
√
√
╳
╳
╳
╳
讲解新课
活动探究一:分式的概念
1.填空
(1)某长方形画的面积为Sm2 ,长为8m,则它的宽为____m.
(2)某长方形画的面积为Sm2 ,长为xm,则它的宽为____m.
(3)如果两块面积为x公顷,y公顷的稻田,分别产稻谷akg,bkg,那么这两块稻田平均每公顷产稻谷__ ___kg.
代数式 ,, 它们有什么共同特征?它们与整式有什么不同?
相同点:他们都是分数的形式,分子或分母都是整式
不同点:分母是否含分母
说一说:
【归纳结论】分式的概念:
一个整式 f 除以一个非零整式 g (g 中含有字母),所得的商记作 ,把代数式 叫作分式,其中 f 是分式的分子,g是分式的分母, g≠0.
下面的式子哪些是分式?
√
√
√
√
√
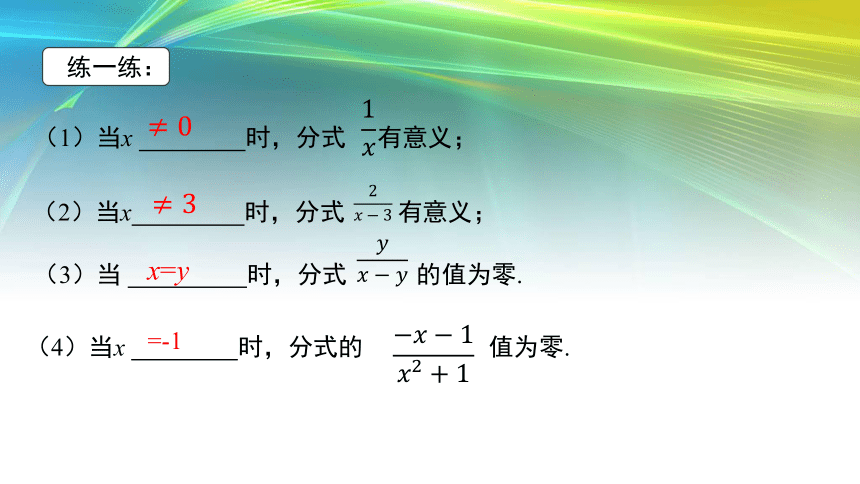
练一练:
活动探究二:分式有意义及分式值为零的条件
例1:当x取什么值时,分式的值满足下列条件:
(1)不存在;(2)等于0
解:(1)当3=0分母时,即= 时,分式的值不存在
(2)当分子=0 ,即=时,分母3≠0,分式的值等于0.
【方法总结】:分式有意义的条件是分母不为零。分式的值等于零,应满足分子等于零,同时分母不为零
x=y
(1)当x 时,分式 有意义;
(2)当x 时,分式 有意义;
(4)当x 时,分式的 值为零.
(3)当 时,分式 的值为零.
练一练:
=-1
例2: 求下列条件下分式 的值:
(1)x = 3; (2)x=-0.4.
活动探究三:求分式的值
解 (1)当 x = 3 时,
(2)当x = -0.4时,
【方法总结】:将未知数的值带入计算。
3. 填表:
x … -3 -2 -1 0 1 2 3 …
…
…
0
1
-2
-1
填表:
练一练:
2.若分式 有意义,则x的取值范围是( )
A . x≠3 B. x≠-3 C . x>3 D . x>-3
A
1.下列代数式中,属于分式的有( )
A. B. C. D.
+1
C
练习新课
3.若分式 的值为零,则x的值为 .
4.已知,当x=5时,分式 的值等于0,k= .
-10
1
5. 填空
(1)某村有m个人,耕地面积约为50公顷,则该村的人均耕地面积 约为 公顷;
(2)某工厂接到加工m个零件的订单,原计划每天加工a个,由于技术改革,实际每天多加工b个,则 天可以完成任务.
1.1 分式
1.定义
3.值为零的条件:
2.有意义的条件:
分式 有意义的条件是 g ≠0.
分式 值为零的条件是 f=0且g ≠0.
:一个整式 f 除以一个非零整式g(g中含字母)所得的商 .
课堂小结
谢谢欣赏
第一章 分式
第1课时 分式的概念
导入新课
想一想:下列式子中哪些是整式?
② ③ ④
⑤ ⑥ ⑦ ⑧
√
√
√
√
╳
╳
╳
╳
讲解新课
活动探究一:分式的概念
1.填空
(1)某长方形画的面积为Sm2 ,长为8m,则它的宽为____m.
(2)某长方形画的面积为Sm2 ,长为xm,则它的宽为____m.
(3)如果两块面积为x公顷,y公顷的稻田,分别产稻谷akg,bkg,那么这两块稻田平均每公顷产稻谷__ ___kg.
代数式 ,, 它们有什么共同特征?它们与整式有什么不同?
相同点:他们都是分数的形式,分子或分母都是整式
不同点:分母是否含分母
说一说:
【归纳结论】分式的概念:
一个整式 f 除以一个非零整式 g (g 中含有字母),所得的商记作 ,把代数式 叫作分式,其中 f 是分式的分子,g是分式的分母, g≠0.
下面的式子哪些是分式?
√
√
√
√
√
练一练:
活动探究二:分式有意义及分式值为零的条件
例1:当x取什么值时,分式的值满足下列条件:
(1)不存在;(2)等于0
解:(1)当3=0分母时,即= 时,分式的值不存在
(2)当分子=0 ,即=时,分母3≠0,分式的值等于0.
【方法总结】:分式有意义的条件是分母不为零。分式的值等于零,应满足分子等于零,同时分母不为零
x=y
(1)当x 时,分式 有意义;
(2)当x 时,分式 有意义;
(4)当x 时,分式的 值为零.
(3)当 时,分式 的值为零.
练一练:
=-1
例2: 求下列条件下分式 的值:
(1)x = 3; (2)x=-0.4.
活动探究三:求分式的值
解 (1)当 x = 3 时,
(2)当x = -0.4时,
【方法总结】:将未知数的值带入计算。
3. 填表:
x … -3 -2 -1 0 1 2 3 …
…
…
0
1
-2
-1
填表:
练一练:
2.若分式 有意义,则x的取值范围是( )
A . x≠3 B. x≠-3 C . x>3 D . x>-3
A
1.下列代数式中,属于分式的有( )
A. B. C. D.
+1
C
练习新课
3.若分式 的值为零,则x的值为 .
4.已知,当x=5时,分式 的值等于0,k= .
-10
1
5. 填空
(1)某村有m个人,耕地面积约为50公顷,则该村的人均耕地面积 约为 公顷;
(2)某工厂接到加工m个零件的订单,原计划每天加工a个,由于技术改革,实际每天多加工b个,则 天可以完成任务.
1.1 分式
1.定义
3.值为零的条件:
2.有意义的条件:
分式 有意义的条件是 g ≠0.
分式 值为零的条件是 f=0且g ≠0.
:一个整式 f 除以一个非零整式g(g中含字母)所得的商 .
课堂小结
谢谢欣赏
同课章节目录
