2022--2023学年人教版九年级数学上册23.2.2 中心对称图形 课件(共17张PPT)
文档属性
| 名称 | 2022--2023学年人教版九年级数学上册23.2.2 中心对称图形 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
第二十三章 旋转
23.2.2 中心对称图形
人教版 九年级上册
学习目标
(1)了解中心对称图形的概念,会判断一个图形是否为中心
对称图形.
(2)知道中心对称图形和两个图形成中心对称、轴对称图形
和中心对称图形的联系与区别.
(3)感悟类比方法在研究数学问题中的作用.
知识回顾
O
A
B
D
C
O
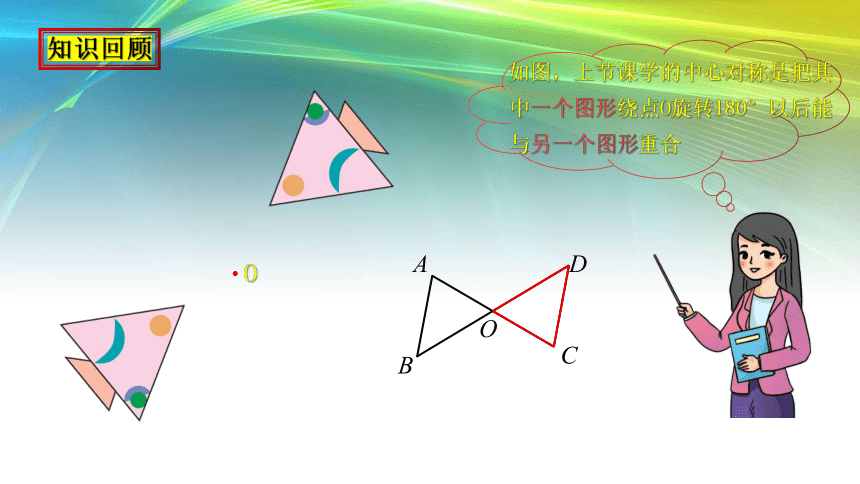
如图,上节课学的中心对称是把其中一个图形绕点O旋转180°以后能与另一个图形重合
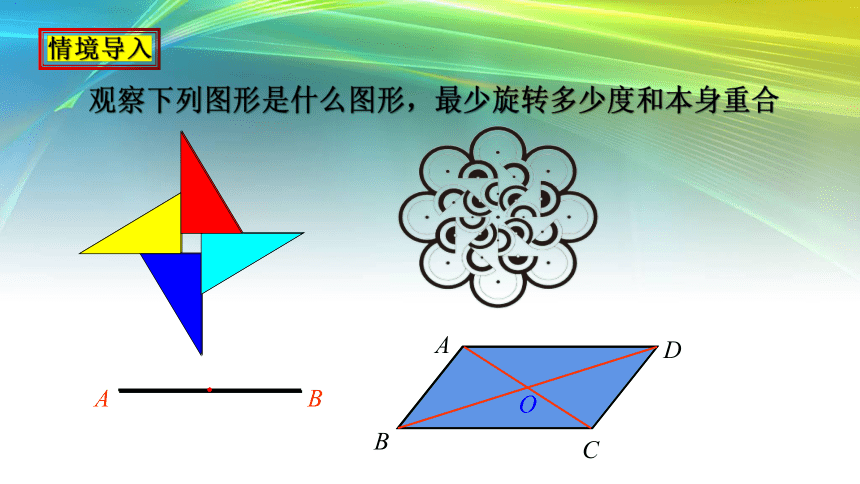
观察下列图形是什么图形,最少旋转多少度和本身重合
情境导入
A
B
A
B
C
D
O
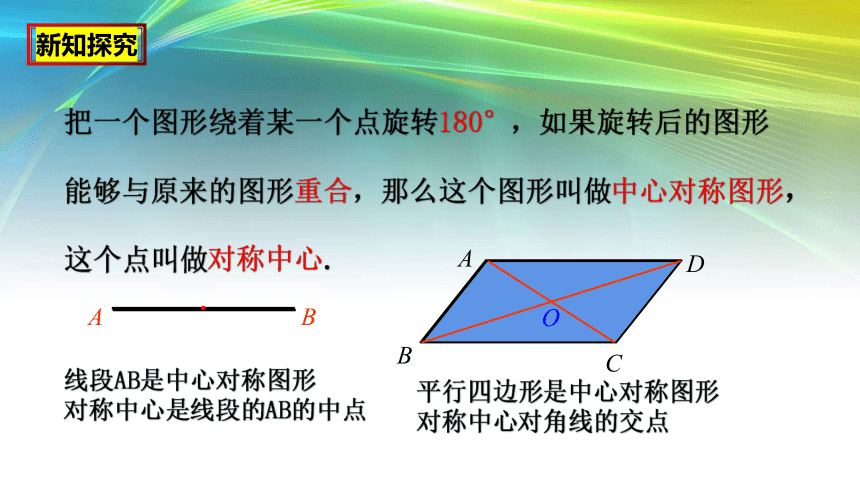
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做对称中心.
新知探究
A
B
线段AB是中心对称图形
对称中心是线段的AB的中点
A
B
C
D
O
平行四边形是中心对称图形
对称中心对角线的交点
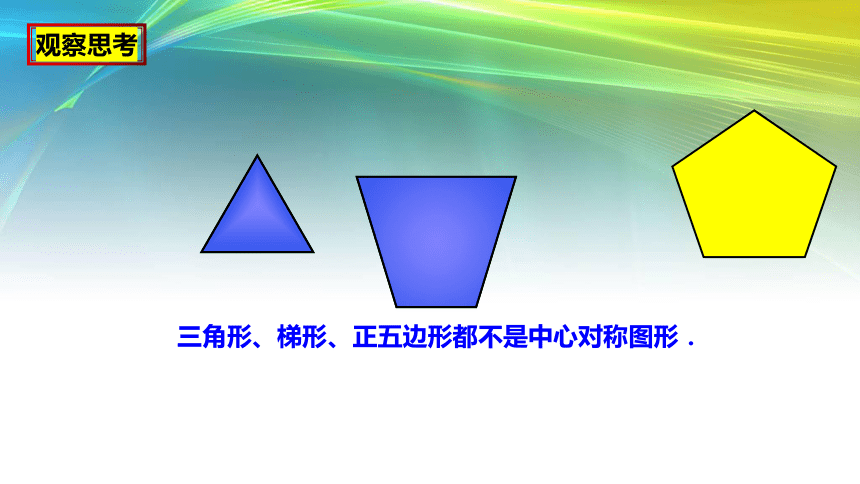
三角形、梯形、正五边形都不是中心对称图形.
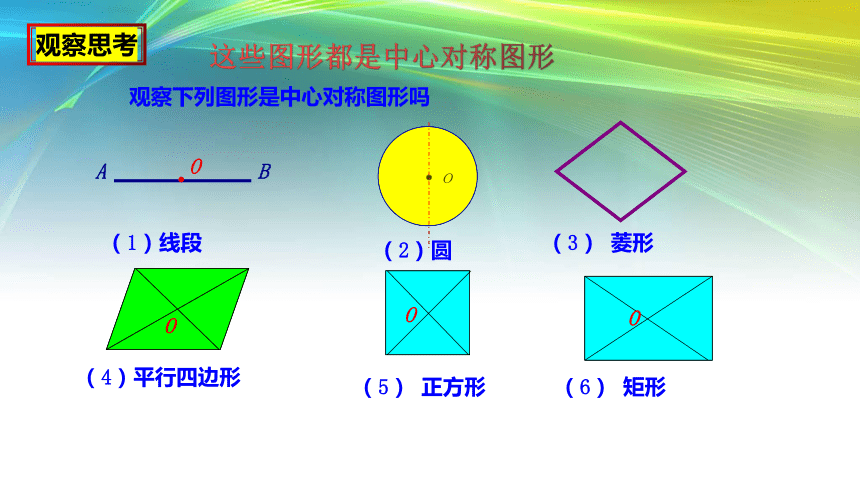
观察思考
o
(2)圆
(5) 正方形
(1)线段
(4)平行四边形
A
B
观察下列图形是中心对称图形吗
O
O
O
观察思考
O
(3) 菱形
(6) 矩形
这些图形都是中心对称图形
观察思考
等边三角形、梯形、正五边形都不是中心对称图形.
中心对称图形形状匀称美观,很多建筑物和工艺品上常采用这种图形作装饰图案,另外,具有中心对称图形形状的物体,能够在所在的平面内绕对称中心平稳地旋转,所以在生产中,旋转的零部件的形状常设计成中心对称图形,如水泵叶轮等.
观察思考
例 判断下列图形是否为中心对称图形.是画√,不是画×
×
√
×
×
×
√
√
√
√
例题分析
√
×
√
名称 中心对称 中心对称图形
定义
联系 把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称
如果一个图形绕着某一个点旋转180°后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形
若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成为中心对称图形,
总结归纳
中心对称图形具有中心对称的一切性质
对 图 称 形 性质 轴对称图形 中心对称图形 图形 对称轴条数 图形 对称中心
线段 2条 中点
角 1条
等腰三角形 1条
等边三角形 3条
平行四边形 对角线交点
矩形 2条 对角线交点
菱形 2条 对角线交点
正方形 4条 对角线交点
圆 无数条 圆心
总结归纳
×
×
×
×
当堂检测
1.在下列四个图案中既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.
D.
2.下列几个图形是国际通用的交通标志,其中不是中心对称图形的是( )
A
B
D
C
!
3. 下列图形中既是中心对称图形的是又是中心对称图形的是( ) A.等边三角形 B.等腰梯形 C.平行四边形 D.正六边形
4.下列图案都是由字母“m”经过变形、组合而成的,其中不是中心对称图形的是( )
当堂检测
5.在英文字母V、W、X、Y、Z中,是中心对称的英文字母的个数有
( )个. A.1 B.2 C.3 D.4
当堂检测
6.从一副扑克牌中抽出如下四张牌,其中是中心对称图形的是()
A B C D
7.阅读材料:对于中心对称图形,过对称中心的作意一条直线都把这个图形分成全等的两都,如图:
当堂检测
尝试应用:用一条直线将下列两个图形分别分成面积相等的两部分
坚持就是胜利
第二十三章 旋转
23.2.2 中心对称图形
人教版 九年级上册
学习目标
(1)了解中心对称图形的概念,会判断一个图形是否为中心
对称图形.
(2)知道中心对称图形和两个图形成中心对称、轴对称图形
和中心对称图形的联系与区别.
(3)感悟类比方法在研究数学问题中的作用.
知识回顾
O
A
B
D
C
O
如图,上节课学的中心对称是把其中一个图形绕点O旋转180°以后能与另一个图形重合
观察下列图形是什么图形,最少旋转多少度和本身重合
情境导入
A
B
A
B
C
D
O
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做对称中心.
新知探究
A
B
线段AB是中心对称图形
对称中心是线段的AB的中点
A
B
C
D
O
平行四边形是中心对称图形
对称中心对角线的交点
三角形、梯形、正五边形都不是中心对称图形.
观察思考
o
(2)圆
(5) 正方形
(1)线段
(4)平行四边形
A
B
观察下列图形是中心对称图形吗
O
O
O
观察思考
O
(3) 菱形
(6) 矩形
这些图形都是中心对称图形
观察思考
等边三角形、梯形、正五边形都不是中心对称图形.
中心对称图形形状匀称美观,很多建筑物和工艺品上常采用这种图形作装饰图案,另外,具有中心对称图形形状的物体,能够在所在的平面内绕对称中心平稳地旋转,所以在生产中,旋转的零部件的形状常设计成中心对称图形,如水泵叶轮等.
观察思考
例 判断下列图形是否为中心对称图形.是画√,不是画×
×
√
×
×
×
√
√
√
√
例题分析
√
×
√
名称 中心对称 中心对称图形
定义
联系 把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称
如果一个图形绕着某一个点旋转180°后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形
若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成为中心对称图形,
总结归纳
中心对称图形具有中心对称的一切性质
对 图 称 形 性质 轴对称图形 中心对称图形 图形 对称轴条数 图形 对称中心
线段 2条 中点
角 1条
等腰三角形 1条
等边三角形 3条
平行四边形 对角线交点
矩形 2条 对角线交点
菱形 2条 对角线交点
正方形 4条 对角线交点
圆 无数条 圆心
总结归纳
×
×
×
×
当堂检测
1.在下列四个图案中既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.
D.
2.下列几个图形是国际通用的交通标志,其中不是中心对称图形的是( )
A
B
D
C
!
3. 下列图形中既是中心对称图形的是又是中心对称图形的是( ) A.等边三角形 B.等腰梯形 C.平行四边形 D.正六边形
4.下列图案都是由字母“m”经过变形、组合而成的,其中不是中心对称图形的是( )
当堂检测
5.在英文字母V、W、X、Y、Z中,是中心对称的英文字母的个数有
( )个. A.1 B.2 C.3 D.4
当堂检测
6.从一副扑克牌中抽出如下四张牌,其中是中心对称图形的是()
A B C D
7.阅读材料:对于中心对称图形,过对称中心的作意一条直线都把这个图形分成全等的两都,如图:
当堂检测
尝试应用:用一条直线将下列两个图形分别分成面积相等的两部分
坚持就是胜利
同课章节目录
