2022-2023学年苏科版八年级数学上册第2章轴对称图形 填空专项练习题 (word,含答案)
文档属性
| 名称 | 2022-2023学年苏科版八年级数学上册第2章轴对称图形 填空专项练习题 (word,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 348.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 21:29:48 | ||
图片预览


文档简介
2022-2023学年苏科版八年级数学上册《第2章轴对称图形》填空专项练习题(附答案)
1.如图,在Rt△ABC中,∠C=90°,DE是线段AB的垂直平分线,已知∠CBD=∠ABD,则∠A= .
2.如图,△ABC中,DE垂直平分边AC,若BC=8,AB=10,则△EBC的周长为 .
3.如图,在△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=12cm,AC=15cm,则CF= cm.
4.如图,BO平分∠ABC,OD⊥BC于点D,点E为射线BA上一动点,若OD=5,则OE的最小值为 .
5.如图,BD是∠ABC的平分线,交AC于D,DE⊥AB于点E,DF⊥BC于点F,S△ABC=36cm2,AB=10cm,BC=8cm,则DE的长为 cm.
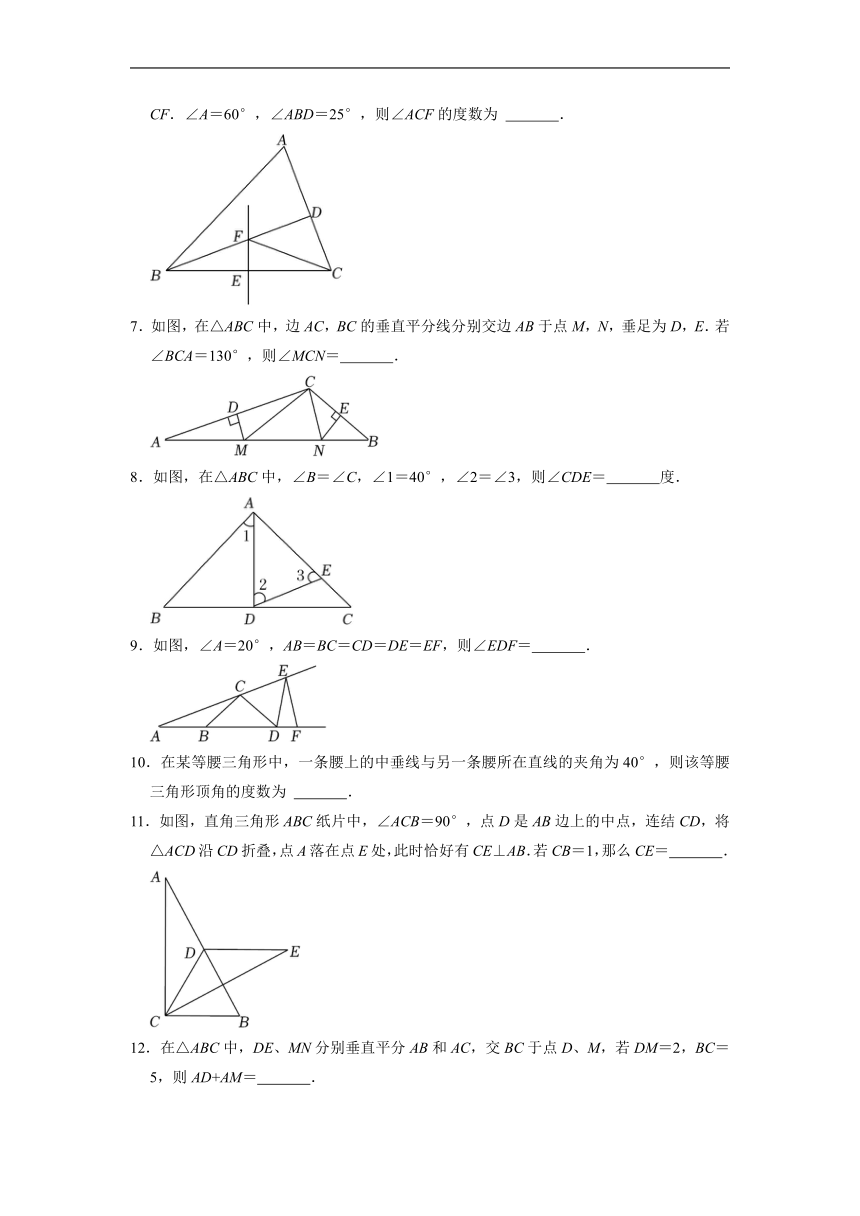
6.如图,△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连接CF.∠A=60°,∠ABD=25°,则∠ACF的度数为 .
7.如图,在△ABC中,边AC,BC的垂直平分线分别交边AB于点M,N,垂足为D,E.若∠BCA=130°,则∠MCN= .
8.如图,在△ABC中,∠B=∠C,∠1=40°,∠2=∠3,则∠CDE= 度.
9.如图,∠A=20°,AB=BC=CD=DE=EF,则∠EDF= .
10.在某等腰三角形中,一条腰上的中垂线与另一条腰所在直线的夹角为40°,则该等腰三角形顶角的度数为 .
11.如图,直角三角形ABC纸片中,∠ACB=90°,点D是AB边上的中点,连结CD,将△ACD沿CD折叠,点A落在点E处,此时恰好有CE⊥AB.若CB=1,那么CE= .
12.在△ABC中,DE、MN分别垂直平分AB和AC,交BC于点D、M,若DM=2,BC=5,则AD+AM= .
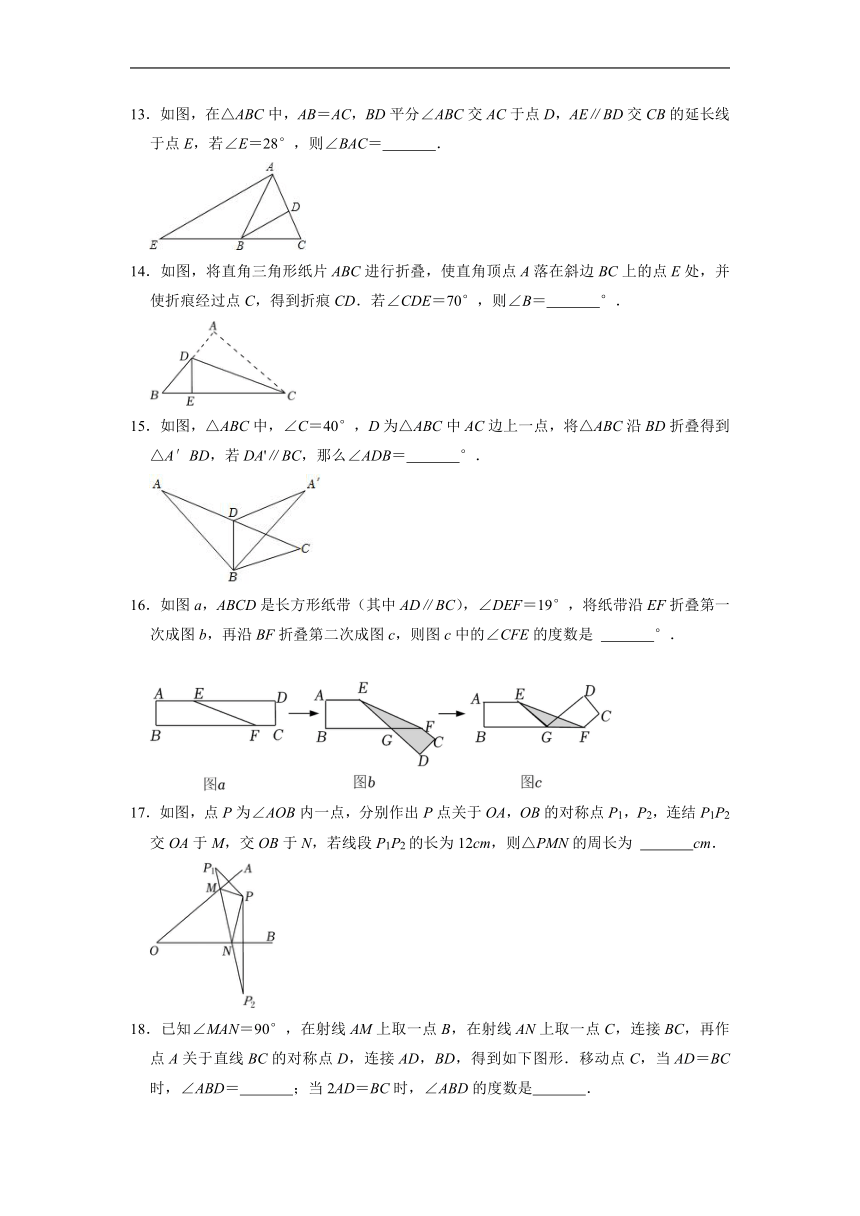
13.如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=28°,则∠BAC= .
14.如图,将直角三角形纸片ABC进行折叠,使直角顶点A落在斜边BC上的点E处,并使折痕经过点C,得到折痕CD.若∠CDE=70°,则∠B= °.
15.如图,△ABC中,∠C=40°,D为△ABC中AC边上一点,将△ABC沿BD折叠得到△A′BD,若DA'∥BC,那么∠ADB= °.
16.如图a,ABCD是长方形纸带(其中AD∥BC),∠DEF=19°,将纸带沿EF折叠第一次成图b,再沿BF折叠第二次成图c,则图c中的∠CFE的度数是 °.
17.如图,点P为∠AOB内一点,分别作出P点关于OA,OB的对称点P1,P2,连结P1P2交OA于M,交OB于N,若线段P1P2的长为12cm,则△PMN的周长为 cm.
18.已知∠MAN=90°,在射线AM上取一点B,在射线AN上取一点C,连接BC,再作点A关于直线BC的对称点D,连接AD,BD,得到如下图形.移动点C,当AD=BC时,∠ABD= ;当2AD=BC时,∠ABD的度数是 .
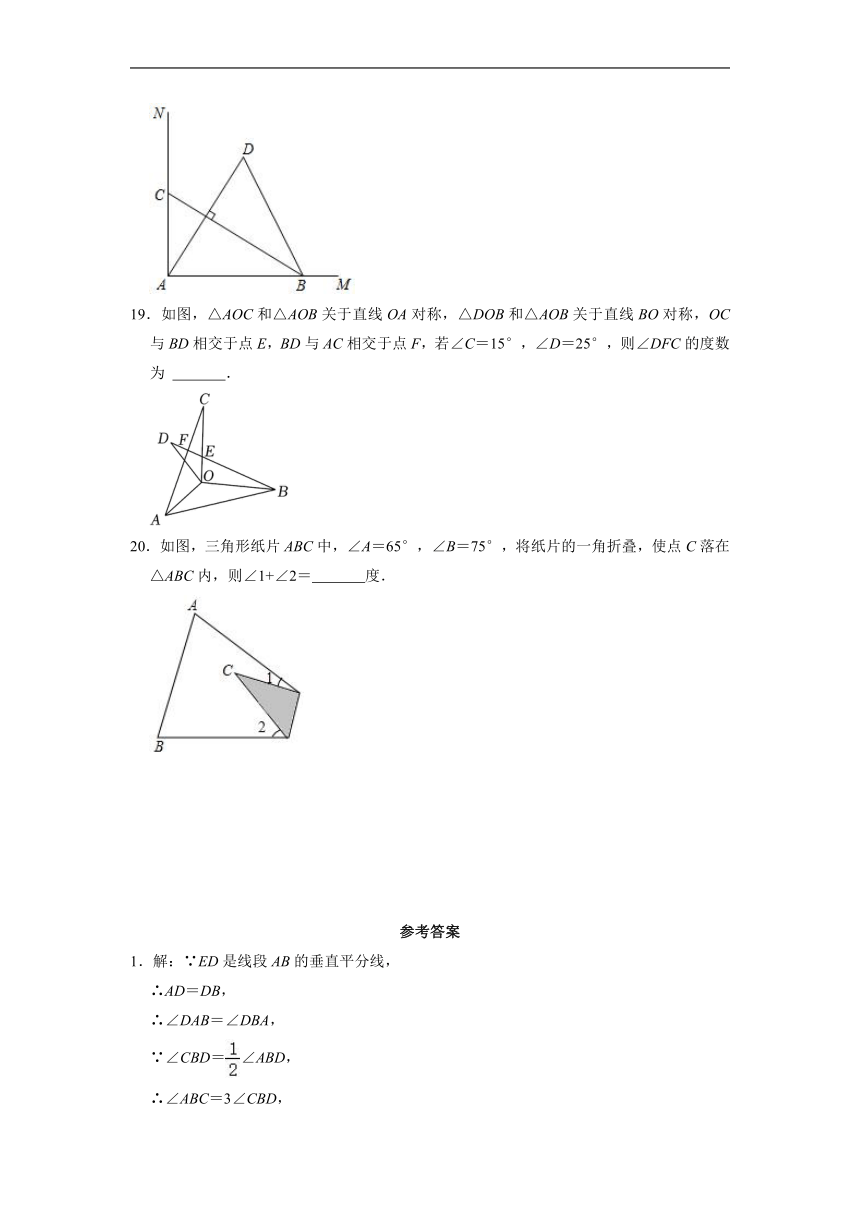
19.如图,△AOC和△AOB关于直线OA对称,△DOB和△AOB关于直线BO对称,OC与BD相交于点E,BD与AC相交于点F,若∠C=15°,∠D=25°,则∠DFC的度数为 .
20.如图,三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,则∠1+∠2= 度.
参考答案
1.解:∵ED是线段AB的垂直平分线,
∴AD=DB,
∴∠DAB=∠DBA,
∵∠CBD=∠ABD,
∴∠ABC=3∠CBD,
∴∠A=2∠CBD,
∵∠C=90°,
∴∠A+∠ABC=90°,即2∠DBC+2∠DBC+∠DBC=90°,
解得,∠DBC=18°,
∴∠A=36°.
故答案为:36°.
2.解:∵DE是△ABC中AC边的垂直平分线,
∴EA=EC,
∴△EBC的周长=BC+BE+EC=BC+BE+EA=BC+BA=18,
故答案为:18.
3.解:∵EF是AB的垂直平分线,
∴FA=BF=12cm,
∵AC=15cm,
∴CF=AC﹣AF=3(cm).
故答案为:3.
4.解:∵BO平分∠ABC,OD⊥BC于点D,OD=5,
∴O到AB的距离等于OD的长,
根据垂线段最短,可知OE最小值为5.
故答案为:5.
5.解:∵BD平分∠ABC,DE⊥AB,DF⊥BC,
∴DE=DF,
设DE=DF=x,
∵S△ABC=S△ABD+S△BCD=AB DE+BC DF,
即36=x (10+8),
解得x=4,
∴DE的长为4cm.
故答案为:4.
6.解:∵BD平分∠ABC,∠ABD=25°,
∴∠DBC=∠ABD=25°,∠ABC=2∠ABD=50°,
∵∠A=60°,
∴∠ACB=180°﹣∠A﹣∠ACB=70°,
∵EF是线段BC的垂直平分线,
∴FB=FC,
∴∠FCB=∠DBC=25°,
∴∠ACF=∠ACB﹣∠FCB=70°﹣25°=45°,
故答案为:45°.
7.解:∵∠BCA=130°,
∴∠A+∠B=180°﹣130°=50°,
∵DM是AC的垂直平分线,
∴MC=MA,
∴∠MCA=∠A,
同理,NC=NB,
∴∠NCB=∠B,
∴∠MCA+∠NCB=50°,
∴∠MCN=∠BCA﹣(∠MCA+∠NCB)=130°﹣50°=80°,
故答案为:80°.
8.解:∵∠3=∠CDE+∠C,∠2=∠3,
∴∠2=∠CDE+∠C,
又∵∠B+∠1=∠ADC,∠1=40°,
∴∠B+40°=∠ADC,
∵∠ADC=∠2+∠CDE,
∴∠B+40°=∠CDE+∠C+∠CDE,
∵∠B=∠C,
∴2∠CDE=40°,
∴∠CDE=20°,
故答案为:20.
9.解:∵AB=BC,∠A=20°,
∴∠ACB=∠A=20°,
∴∠CBD=∠A+∠ACB=40°,
∵BC=DC,
∴∠CBD=∠CDB=40°,
∴∠BCD=100°,
∴∠ECD=180°﹣∠ACB﹣∠BCD=180°﹣20°﹣100°=60°,
∵CD=DE,
∴∠CED=∠DCE=60°,
∴∠EDF=∠A+∠CED=20°+60°=80°.
故答案为:80°.
10.解:当为锐角等腰三角形时,如图:
∵∠ADE=40°,∠AED=90°,
∴∠A=50°,
当为钝角等腰三角形时,如图:
∠ADE=40°,∠DAE=50°,
∴顶角∠BAC=180°﹣50°=130°.
故该等腰三角形顶角的度数为50°或130°.
故答案为:50°或130°.
11.解:如图,设CE交AB于点O.
∵∠ACB=90°,AD=DB,
∴CD=AD=DB,
∴∠A=∠ACD,
由翻折的性质可知∠ACD=∠DCE,
∵CE⊥AB,
∴∠BCE+∠B=90°,
∵∠A+∠B=90°,
∴∠BCE=∠A,
∴∠BCE=∠ACD=∠DCE=30°,
∴CO=,
∵DA=DE,DA=DC,
∴DC=DE,
∵DO⊥CE,
∴CO=OE=,
∴CE=.
故答案为:.
12.解:∵DE、MN分别垂直平分AB和AC,
∴AD=BD,AM=CM,
如图1,AD+AM=BD+CM=BC﹣DM=5﹣2=3,
如图2,AD+AM=BD+CM=BC+DM=5+2=7,
综上所述,AD+AM=3或7,
故答案为:3或7.
13.解:∵AE∥BD,
∴∠DBC=∠E=28°,
∵BD平分∠ABC,
∴∠ABC=2∠DBC=56°,
∵AB=AC,
∴∠C=∠ABC=56°,
∴∠BAC=180°﹣∠ABC﹣∠C=68°.
故答案为:68°.
14.解:∵△ABC为直角三角形,
∴∠A=90°,
∵∠CDE=70°,
由折叠性质可得∠CED=∠A=90°,∠ADC=∠CDE=70°,
∴∠BED=90°,∠BDE=180°﹣∠ADC﹣∠CDE=40°,
∴∠B=180°﹣∠BED﹣∠BDE=50°,
故答案为:50.
15.解:∵DA'∥BC,∴∠A′BC=∠A′,
由折叠的性质得∠A=∠A′=∠A′BC,∠ABD=∠A′BD,
∵∠A+∠ABC+∠C=180°,∠C=40°,
∴∠A+∠ABD+∠A′BD+∠C=180°,
∴2(∠A′BC+∠A′BD)+40°=180°,
∴∠A′BC+∠A′BD=70°,
∴∠ADB=∠DBC+∠C=∠A′BC+∠A′BD+∠C=70°+40°=110°,
故答案为:110.
16.解:∵AD∥BC,∠DEF=19°,
∴∠BFE=∠DEF=19°,
∴∠EFC=161°(图a),
∴∠BFC=161°﹣19°=142°(图b),
∴∠CFE=142°﹣19°=123°(图c).
故答案为:123.
17.解:∵P点关于OA、OB的对称点P1,P2,
∴NP=NP2,MP=MP1,
∴△PMN的周长=PN+MN+MP=P2N+NM+MP1=P1P2=12cm,
故答案为:12.
18.解:①如图1中,设AD交BC于点O.
∵A,D关于BC对称,
∴OA=OD,AD⊥BC,
∵∠MAN=∠AOC=∠AOB=90°,
∴∠CAO+∠OAB=90°,∠CAO+∠ACO=90°,
∴∠ACO=∠OAB,
∴△AOC∽△BOA,
∴OA2=OB OC,
∵AD=BC,
∴(BC)2=OC (BC﹣OC),
∴BC2﹣4OC BC+4OC2=0,
∴(BC﹣2OC)2=0,
∴BC=2OC,
∴OB=OC=OA,
∴∠ABO=∠OCD=45°,
∴∠ABD=90°.
②分两种情况:
如图,当AB>AC时,取BC的中点E,连接AE,DE,
则AE=DE=BC,
即BC=2AE=2DE,
又∵BC=2AD,
∴AD=AE=DE,
∴△ADE是等边三角形,
∴∠AED=60°,
又∵BC垂直平分AD,
∴∠AEC=30°,
又∵BE=AE,
∴∠ABC=∠AEC=15°,
∴∠ABD=2∠ABC=30°;
如图,当AB<AC时,同理可得∠ACD=30°,
又∵∠BAC=∠BDC=90°,
∴∠ABD=150°,
故答案为:90°,30°或150°.
19.解:∵△AOC和△AOB关于直线AO对称,△DOB和△AOB关于直线BO对称,
∴∠C=∠ABO=∠DBO=15°,∠D=∠BAO=∠OAC=25°,
∴∠CAB=50°,
∴∠BOC=∠BAC+∠C+∠ABO=80°,
∴∠BEC=∠BOC+∠OBD=80°+15°=95°,
∵∠BEC=∠EFC+∠C,
∴∠EFC=95°﹣15°=80°,
∴∠DFC=180°﹣80°=100°
故答案为100°.
20.解:延长AF、BE交于点D,
∵∠A=65°,∠B=75°,
∴∠D=180°﹣∠A﹣∠B=40°,
∴∠DFE+∠DEF=180°﹣∠D=140°,
∵将纸片的一角折叠,使点C落在△ABC内,
∴∠CFE=∠DFE,∠CEF=∠DEF,
∴∠DFC+∠DEC=2(∠DFE+∠DEF)=280°,
∴∠1+∠2=(180°﹣∠DFC)+(180°﹣∠DEC)=360°﹣(∠DFC+∠DEC)=360°﹣280°=80°,
故答案为:80.
1.如图,在Rt△ABC中,∠C=90°,DE是线段AB的垂直平分线,已知∠CBD=∠ABD,则∠A= .
2.如图,△ABC中,DE垂直平分边AC,若BC=8,AB=10,则△EBC的周长为 .
3.如图,在△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=12cm,AC=15cm,则CF= cm.
4.如图,BO平分∠ABC,OD⊥BC于点D,点E为射线BA上一动点,若OD=5,则OE的最小值为 .
5.如图,BD是∠ABC的平分线,交AC于D,DE⊥AB于点E,DF⊥BC于点F,S△ABC=36cm2,AB=10cm,BC=8cm,则DE的长为 cm.
6.如图,△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连接CF.∠A=60°,∠ABD=25°,则∠ACF的度数为 .
7.如图,在△ABC中,边AC,BC的垂直平分线分别交边AB于点M,N,垂足为D,E.若∠BCA=130°,则∠MCN= .
8.如图,在△ABC中,∠B=∠C,∠1=40°,∠2=∠3,则∠CDE= 度.
9.如图,∠A=20°,AB=BC=CD=DE=EF,则∠EDF= .
10.在某等腰三角形中,一条腰上的中垂线与另一条腰所在直线的夹角为40°,则该等腰三角形顶角的度数为 .
11.如图,直角三角形ABC纸片中,∠ACB=90°,点D是AB边上的中点,连结CD,将△ACD沿CD折叠,点A落在点E处,此时恰好有CE⊥AB.若CB=1,那么CE= .
12.在△ABC中,DE、MN分别垂直平分AB和AC,交BC于点D、M,若DM=2,BC=5,则AD+AM= .
13.如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=28°,则∠BAC= .
14.如图,将直角三角形纸片ABC进行折叠,使直角顶点A落在斜边BC上的点E处,并使折痕经过点C,得到折痕CD.若∠CDE=70°,则∠B= °.
15.如图,△ABC中,∠C=40°,D为△ABC中AC边上一点,将△ABC沿BD折叠得到△A′BD,若DA'∥BC,那么∠ADB= °.
16.如图a,ABCD是长方形纸带(其中AD∥BC),∠DEF=19°,将纸带沿EF折叠第一次成图b,再沿BF折叠第二次成图c,则图c中的∠CFE的度数是 °.
17.如图,点P为∠AOB内一点,分别作出P点关于OA,OB的对称点P1,P2,连结P1P2交OA于M,交OB于N,若线段P1P2的长为12cm,则△PMN的周长为 cm.
18.已知∠MAN=90°,在射线AM上取一点B,在射线AN上取一点C,连接BC,再作点A关于直线BC的对称点D,连接AD,BD,得到如下图形.移动点C,当AD=BC时,∠ABD= ;当2AD=BC时,∠ABD的度数是 .
19.如图,△AOC和△AOB关于直线OA对称,△DOB和△AOB关于直线BO对称,OC与BD相交于点E,BD与AC相交于点F,若∠C=15°,∠D=25°,则∠DFC的度数为 .
20.如图,三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,则∠1+∠2= 度.
参考答案
1.解:∵ED是线段AB的垂直平分线,
∴AD=DB,
∴∠DAB=∠DBA,
∵∠CBD=∠ABD,
∴∠ABC=3∠CBD,
∴∠A=2∠CBD,
∵∠C=90°,
∴∠A+∠ABC=90°,即2∠DBC+2∠DBC+∠DBC=90°,
解得,∠DBC=18°,
∴∠A=36°.
故答案为:36°.
2.解:∵DE是△ABC中AC边的垂直平分线,
∴EA=EC,
∴△EBC的周长=BC+BE+EC=BC+BE+EA=BC+BA=18,
故答案为:18.
3.解:∵EF是AB的垂直平分线,
∴FA=BF=12cm,
∵AC=15cm,
∴CF=AC﹣AF=3(cm).
故答案为:3.
4.解:∵BO平分∠ABC,OD⊥BC于点D,OD=5,
∴O到AB的距离等于OD的长,
根据垂线段最短,可知OE最小值为5.
故答案为:5.
5.解:∵BD平分∠ABC,DE⊥AB,DF⊥BC,
∴DE=DF,
设DE=DF=x,
∵S△ABC=S△ABD+S△BCD=AB DE+BC DF,
即36=x (10+8),
解得x=4,
∴DE的长为4cm.
故答案为:4.
6.解:∵BD平分∠ABC,∠ABD=25°,
∴∠DBC=∠ABD=25°,∠ABC=2∠ABD=50°,
∵∠A=60°,
∴∠ACB=180°﹣∠A﹣∠ACB=70°,
∵EF是线段BC的垂直平分线,
∴FB=FC,
∴∠FCB=∠DBC=25°,
∴∠ACF=∠ACB﹣∠FCB=70°﹣25°=45°,
故答案为:45°.
7.解:∵∠BCA=130°,
∴∠A+∠B=180°﹣130°=50°,
∵DM是AC的垂直平分线,
∴MC=MA,
∴∠MCA=∠A,
同理,NC=NB,
∴∠NCB=∠B,
∴∠MCA+∠NCB=50°,
∴∠MCN=∠BCA﹣(∠MCA+∠NCB)=130°﹣50°=80°,
故答案为:80°.
8.解:∵∠3=∠CDE+∠C,∠2=∠3,
∴∠2=∠CDE+∠C,
又∵∠B+∠1=∠ADC,∠1=40°,
∴∠B+40°=∠ADC,
∵∠ADC=∠2+∠CDE,
∴∠B+40°=∠CDE+∠C+∠CDE,
∵∠B=∠C,
∴2∠CDE=40°,
∴∠CDE=20°,
故答案为:20.
9.解:∵AB=BC,∠A=20°,
∴∠ACB=∠A=20°,
∴∠CBD=∠A+∠ACB=40°,
∵BC=DC,
∴∠CBD=∠CDB=40°,
∴∠BCD=100°,
∴∠ECD=180°﹣∠ACB﹣∠BCD=180°﹣20°﹣100°=60°,
∵CD=DE,
∴∠CED=∠DCE=60°,
∴∠EDF=∠A+∠CED=20°+60°=80°.
故答案为:80°.
10.解:当为锐角等腰三角形时,如图:
∵∠ADE=40°,∠AED=90°,
∴∠A=50°,
当为钝角等腰三角形时,如图:
∠ADE=40°,∠DAE=50°,
∴顶角∠BAC=180°﹣50°=130°.
故该等腰三角形顶角的度数为50°或130°.
故答案为:50°或130°.
11.解:如图,设CE交AB于点O.
∵∠ACB=90°,AD=DB,
∴CD=AD=DB,
∴∠A=∠ACD,
由翻折的性质可知∠ACD=∠DCE,
∵CE⊥AB,
∴∠BCE+∠B=90°,
∵∠A+∠B=90°,
∴∠BCE=∠A,
∴∠BCE=∠ACD=∠DCE=30°,
∴CO=,
∵DA=DE,DA=DC,
∴DC=DE,
∵DO⊥CE,
∴CO=OE=,
∴CE=.
故答案为:.
12.解:∵DE、MN分别垂直平分AB和AC,
∴AD=BD,AM=CM,
如图1,AD+AM=BD+CM=BC﹣DM=5﹣2=3,
如图2,AD+AM=BD+CM=BC+DM=5+2=7,
综上所述,AD+AM=3或7,
故答案为:3或7.
13.解:∵AE∥BD,
∴∠DBC=∠E=28°,
∵BD平分∠ABC,
∴∠ABC=2∠DBC=56°,
∵AB=AC,
∴∠C=∠ABC=56°,
∴∠BAC=180°﹣∠ABC﹣∠C=68°.
故答案为:68°.
14.解:∵△ABC为直角三角形,
∴∠A=90°,
∵∠CDE=70°,
由折叠性质可得∠CED=∠A=90°,∠ADC=∠CDE=70°,
∴∠BED=90°,∠BDE=180°﹣∠ADC﹣∠CDE=40°,
∴∠B=180°﹣∠BED﹣∠BDE=50°,
故答案为:50.
15.解:∵DA'∥BC,∴∠A′BC=∠A′,
由折叠的性质得∠A=∠A′=∠A′BC,∠ABD=∠A′BD,
∵∠A+∠ABC+∠C=180°,∠C=40°,
∴∠A+∠ABD+∠A′BD+∠C=180°,
∴2(∠A′BC+∠A′BD)+40°=180°,
∴∠A′BC+∠A′BD=70°,
∴∠ADB=∠DBC+∠C=∠A′BC+∠A′BD+∠C=70°+40°=110°,
故答案为:110.
16.解:∵AD∥BC,∠DEF=19°,
∴∠BFE=∠DEF=19°,
∴∠EFC=161°(图a),
∴∠BFC=161°﹣19°=142°(图b),
∴∠CFE=142°﹣19°=123°(图c).
故答案为:123.
17.解:∵P点关于OA、OB的对称点P1,P2,
∴NP=NP2,MP=MP1,
∴△PMN的周长=PN+MN+MP=P2N+NM+MP1=P1P2=12cm,
故答案为:12.
18.解:①如图1中,设AD交BC于点O.
∵A,D关于BC对称,
∴OA=OD,AD⊥BC,
∵∠MAN=∠AOC=∠AOB=90°,
∴∠CAO+∠OAB=90°,∠CAO+∠ACO=90°,
∴∠ACO=∠OAB,
∴△AOC∽△BOA,
∴OA2=OB OC,
∵AD=BC,
∴(BC)2=OC (BC﹣OC),
∴BC2﹣4OC BC+4OC2=0,
∴(BC﹣2OC)2=0,
∴BC=2OC,
∴OB=OC=OA,
∴∠ABO=∠OCD=45°,
∴∠ABD=90°.
②分两种情况:
如图,当AB>AC时,取BC的中点E,连接AE,DE,
则AE=DE=BC,
即BC=2AE=2DE,
又∵BC=2AD,
∴AD=AE=DE,
∴△ADE是等边三角形,
∴∠AED=60°,
又∵BC垂直平分AD,
∴∠AEC=30°,
又∵BE=AE,
∴∠ABC=∠AEC=15°,
∴∠ABD=2∠ABC=30°;
如图,当AB<AC时,同理可得∠ACD=30°,
又∵∠BAC=∠BDC=90°,
∴∠ABD=150°,
故答案为:90°,30°或150°.
19.解:∵△AOC和△AOB关于直线AO对称,△DOB和△AOB关于直线BO对称,
∴∠C=∠ABO=∠DBO=15°,∠D=∠BAO=∠OAC=25°,
∴∠CAB=50°,
∴∠BOC=∠BAC+∠C+∠ABO=80°,
∴∠BEC=∠BOC+∠OBD=80°+15°=95°,
∵∠BEC=∠EFC+∠C,
∴∠EFC=95°﹣15°=80°,
∴∠DFC=180°﹣80°=100°
故答案为100°.
20.解:延长AF、BE交于点D,
∵∠A=65°,∠B=75°,
∴∠D=180°﹣∠A﹣∠B=40°,
∴∠DFE+∠DEF=180°﹣∠D=140°,
∵将纸片的一角折叠,使点C落在△ABC内,
∴∠CFE=∠DFE,∠CEF=∠DEF,
∴∠DFC+∠DEC=2(∠DFE+∠DEF)=280°,
∴∠1+∠2=(180°﹣∠DFC)+(180°﹣∠DEC)=360°﹣(∠DFC+∠DEC)=360°﹣280°=80°,
故答案为:80.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
