2022-2023学年苏科版八年级数学上册第2章轴对称图形 选择专项练习题 (word版含答案)
文档属性
| 名称 | 2022-2023学年苏科版八年级数学上册第2章轴对称图形 选择专项练习题 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 372.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 16:35:33 | ||
图片预览

文档简介
2022-2023学年苏科版八年级数学上册《第2章轴对称图形》选择专项练习题(附答案)
1.如图,在△ABC中,∠ABC=∠C,BD平分∠ABC交AC于点D.若BD=AD,则∠ABC的大小为( )
A.66° B.70° C.72° D.75°
2.如图,在△ABC中,∠C=90°,AD是△ABC的角平分线.AB=10,CD=3,则△ABD的面积为( )
A.30 B.18 C.15 D.9
3.如图,在△ABC中,DE垂直平分BC,分别交AC,BC于点D,E,若AB=5,AC=7,则△ABD的周长是( )
A.10 B.12 C.14 D.17
4.如图,在△ABC中,已知AC=27,AB边的垂直平分线交AB于点D,交AC于点E,若△BCE的周长等于45,则BC的长为( )
A.33 B.28 C.18 D.13
5.如图,点D是△ABC三边垂直平分线的交点,若∠D=116°,则∠A=( )
A.64° B.58° C.52° D.68°
6.已知等腰三角形三边的长分别为4,x,10,则x的值是( )
A.4 B.10 C.4 或10 D.6 或10
7.如图,△ABC中,∠ABC的角平分线与∠ACB的角平分线交于点P,若点P到边BC的距离为1,△ABC的周长为12,则△ABC的面积为( )
A.6 B.7 C.8 D.9
8.如图,∠AOB是一钢架,∠AOB=18°,为使钢架更加牢固,需在其内部添加一些钢管EF,FG,GH,…,添加的钢管长度都与OE的长度相等,则最多能添加的钢管根数为( )
A.4 B.5 C.6 D.无数
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠BCD,AD过点P,且与AB垂直,若BP=5,CP=12,则AD的长为( )
A.12 B.13 C. D.
10.如图,在△ABC中,∠BAC=90°,高AD与角平分线BE相交于点F,∠DAC的平分线AG分别交BC、BE于点G、O,连接FG,下列结论:①∠ABD=∠DAC;②∠AFE=∠AEF;③AG⊥EF;④FG∥AC,其中所有正确结论的序号是( )
A.①② B.①③ C.①②③ D.①②③④
11.如图,Rt△ABC中,∠C=90°,∠A=38°,点D在AB上,且点D与点B关于直线l对称,则∠ACD的度数为( )
A.10° B.14° C.38° D.52°
12.等腰三角形一腰上的高与另一腰的夹角为54°,则该等腰三角形底角的度数为( )
A.72° B.72°或36° C.36° D.72°或18°
13.如图,在△ABC中,AB=AC,∠A=36°,BD,CE分别平分∠ABC,∠ACB.若CD=5.则CE等于( )
A.4 B.4.5 C.5 D.5.5
14.如图,在△ABC中,分别以点B和点C为圆心,大于BC长为半径画弧,两弧相交于点M,N.作直线MN,交AC于点D,交BC于点E,连接BD.若AB=7,AC=12,BC=6,则△ABD的周长为( )
A.25 B.22 C.19 D.18
15.下列图案中,是轴对称图形的是( )
A. B. C. D.
16.如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F,若AB=5,AC=8,BC=10,则△AEF的周长为( )
A.5 B.8 C.10 D.13
17.如图,点C为BD上一点,AB=AC,AE=CE,AE∥BD,∠E=30°,则∠BAC的度数是( )
A.25° B.30° C.45° D.50°
18.如图,将△ABD沿△ABC的角平分线AD翻折,点B恰好落在AC边上的点E处.已知∠C=20°,AB+BD=AC,那么∠B的度数为( )
A.30° B.40° C.60° D.80°
19.如图,在三角形ABC中,∠C=60°,∠B=30°,D是BC上一点,将三角形ABD沿AD翻折后得到三角形AED,边AE交射线BC于点F,若DE∥AC,则∠BDA=( )
A.120° B.135° C.110° D.150°
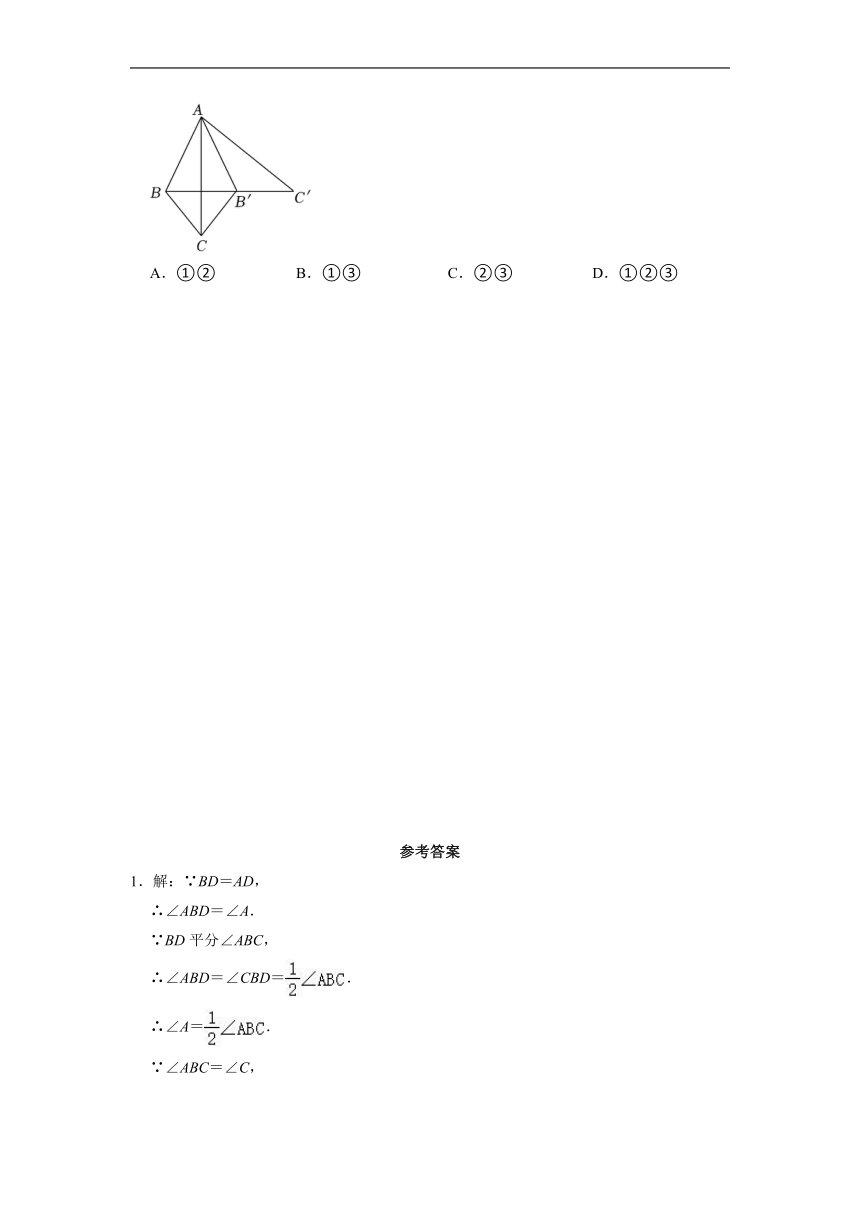
20.如图,将△ABC沿AC所在的直线翻折得到△AB'C,再将△AB′C沿AB'所在的直线翻折得到△AB'C',点B,B',C'在同一条直线上,∠BAC=α,由此给出下列说法:①△ABC≌△AB′C′.②AC⊥BB'.③∠CB′B=2α.其中正确的说法是( )
A.①② B.①③ C.②③ D.①②③
参考答案
1.解:∵BD=AD,
∴∠ABD=∠A.
∵BD平分∠ABC,
∴∠ABD=∠CBD=.
∴∠A=.
∵∠ABC=∠C,
∴.
∴∠ABC=72°.
故选:C.
2.解:作DE⊥AB于E.
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=CD=3.
∴△ABD的面积为 ×3×10=15.
故选:C.
3.解:∵DE垂直平分BC,
∴DB=DC,
∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=5+7=12,
故选:B.
4.解:∵DE是AB边的垂直平分线,
∴EA=EB,
∵△BCE的周长等于45,
∴BC+CE+BE=BC+CE+EA=BC+AC=45,
∵AC=27,
∴BC=45﹣27=18,
故选:C.
5.解:连接AD并延长至E,
∵点D是△ABC三边垂直平分线的交点,
∴DA=DB,DA=DC,
∴∠DAB=∠DBA,∠DAC=∠DCA,
∴∠DAB=∠BDE,∠DAC=∠CDE,
∴∠BAC=∠BDC=×116°=58°,
故选:B.
6.解:当x=4时,4+4<10,不符合三角形三边关系,舍去;
当x=10时,4+10>10,符合三角形三边关系.
故选:B.
7.解:过点P作PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,如图所示:
∵∠ABC的角平分线与∠ACB的角平分线交于点P,
∴PD=PE=PF,
∵点P到边BC的距离为1,
∴PF=1,
∴PD=PE=1,
∵△ABC的周长为12,
∴△ABC的面积=
=
=6,
故选:A.
8.解:∵添加的钢管长度都与OE相等,∠AOB=18°,
∴∠GEF=∠FGE=36°,…从图中我们会发现有好几个等腰三角形,即第一个等腰三角形的底角是18°,第二个是36°,第三个是54°,四个是72°,五个是90°就不存在了.
所以一共有4个.
故选:A.
9.解:过P点作PH⊥BC于H,如图,
∵AB∥CD,AD⊥AB,
∴AD⊥CD,∠ABC+∠DCB=180°,
∵BP和CP分别平分∠ABC和∠BCD,
∴PH=PA=PD,∠PCB=∠DCB,∠PBC=∠ABC,
∴∠PBC+∠PCB=(∠ABC+∠DCB)=×180°=90°,
∴∠BPC=90°,
∴BC===13,
∵PH BC=PB PC,
∴PH==,
∴PA=PD=PH=,
∴AD=2PA=.
故选:D.
10.解:∵AD为高,
∴∠ADB=90°,
∵∠BAD+∠ABD=90°,∠BAD+∠DAC=90°,
∴∠ABD=∠DAC,所以①正确;
∵∠ABD+∠C=90°,
∴∠BAD=∠C,
∵∠AFE=∠ABF+∠BAF,∠AEF=∠C+∠EAC,
∴∠AFE=∠AEF,所以②正确;
∴AE=AF,
∵AG平分∠DAC,
∴AO⊥EF,所以③正确;
∵BO平分∠ABG,
∴∠ABO=∠GBO,
∵BO⊥AG,
∴∠BAO=∠BGO,
∴BA=BG,
∴OA=OG,
∴BO垂直平分AG,
∴FA=FG,
∴∠FAO=∠FGO,
∵∠FAO=∠EAO,
∴∠EAO=∠FGO,
∴FG∥AC,所以④正确.
故选:D.
11.解:∵∠C=90°,∠A=38°,
∴∠B=52°,
∵点D与点B关于直线l对称,
∴∠CDB=∠B=52°,
∵∠CDB=∠ACD+∠A,
∴52°=∠ACD+38°,
∴∠ACD=14°,
故选:B.
12.解:在等腰△ABC中,AB=AC,BD为腰AC上的高,∠ABD=54°,
当BD在△ABC内部时,如图1,
∵BD为高,
∴∠ADB=90°,
∴∠BAD=90°﹣54°=36°,
∵AB=AC,
∴∠ABC=∠ACB=(180°﹣36°)=72°;
当BD在△ABC外部时,如图2,
∵BD为高,
∴∠ADB=90°,
∴∠BAD=90°﹣54°=36°,
∵AB=AC,
∴∠ABC=∠ACB,
而∠BAD=∠ABC+∠ACB,
∴∠ACB=∠BAD=18°,
综上所述,这个等腰三角形底角的度数为72°或18°.
故选:D.
13.解:∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°,
∵BD,CE分别平分∠ABC,∠ACB,
∴∠DBC=∠ACE=36°,
∴∠BDC=180°﹣36°﹣72°=72°,
∴∠CED=180°﹣∠ACE﹣∠BDC=72°,
∴∠CED=∠CDE,
∴CE=CD=5,
故选:C.
14.解:由题意可得,
MN垂直平分BC,
∴DB=DC,
∵△ABD的周长是AB+BD+AD,
∴AB+BD+AD=AB+DC+AD=AB+AC,
∵AB=7,AC=12,
∴AB+AC=19,
∴∵△ABD的周长是19,
故选:C.
15.解:A.是轴对称图形,故此选项符合题意;
B.不是轴对称图形,故此选项不符合题意;
C.不是轴对称图形,故此选项不符合题意;
D.不是轴对称图形,故此选项不符合题意;
故选:A.
16.解:∵EG是线段AB的垂直平分线,
∴EA=EB,
同理,FA=FC,
∴△AEF的周长=EA+EF+FA=EB+EF+FC=BC=10,
故选:C.
17.解:∵AE=CE,∠E=30°,
∴△ACE中,∠CAE=75°,
∵AE∥BD,
∴∠ACB=∠CAE=75°,
∵AB=AC,
∴∠B=∠ACB=75°,
∴△ABC中,∠BAC=180°﹣75°×2=30°,
故选:B.
18.解:由翻折可得AB=AE,BD=DE,∠B=∠AED,
∵AB+BD=AC,AC=AE+CE=AB+CE,
∴BD=CE,
∴DE=CE,
∴∠C=∠EDC,
∵∠C=20°,
∴∠EDC=20°,
∴∠AED=∠C+∠EDC=40°,
∴∠B=40°.
故选:B.
19.解:∵∠C=60°,∠B=30°,
∵∠BAC=90°,
由折叠性质可得:
∠E=∠B=30°,∠BAD=∠EAD,
∵DE∥AC,
∴∠CAE=∠E=30°,
∴∠BAE=∠BAC﹣∠CAE=60°,
∴∠BAD=∠EAD=30°,
∴∠BDA=180°﹣∠B﹣∠BAD=120°,
故选:A.
20.解:①由翻折可知:△ABC≌△AB′C,△AB′C≌△AB′C′,
∴△ABC≌△AB′C′;故①正确;
②由翻折可知:点B与点B′关于AC对称,
∴AC⊥BB';故②正确;
③由翻折可知:∠B′AC′=∠B′AC=∠BAC=α,∠AB′C′=∠AB′C,
∴∠AB′B=90°﹣∠B′AC=90°﹣α,
∴∠AB′C′=180°﹣∠AB′B=180°﹣(90°﹣α)=90°+α,
∴∠AB′C=90°+α,
∴∠CB′B=∠AB′C﹣∠AB′B=90°+α﹣(90°﹣α)=2α,
∴∠CB′B=2α.故③正确.
综上所述:正确的说法是:①②③.
故选:D.
1.如图,在△ABC中,∠ABC=∠C,BD平分∠ABC交AC于点D.若BD=AD,则∠ABC的大小为( )
A.66° B.70° C.72° D.75°
2.如图,在△ABC中,∠C=90°,AD是△ABC的角平分线.AB=10,CD=3,则△ABD的面积为( )
A.30 B.18 C.15 D.9
3.如图,在△ABC中,DE垂直平分BC,分别交AC,BC于点D,E,若AB=5,AC=7,则△ABD的周长是( )
A.10 B.12 C.14 D.17
4.如图,在△ABC中,已知AC=27,AB边的垂直平分线交AB于点D,交AC于点E,若△BCE的周长等于45,则BC的长为( )
A.33 B.28 C.18 D.13
5.如图,点D是△ABC三边垂直平分线的交点,若∠D=116°,则∠A=( )
A.64° B.58° C.52° D.68°
6.已知等腰三角形三边的长分别为4,x,10,则x的值是( )
A.4 B.10 C.4 或10 D.6 或10
7.如图,△ABC中,∠ABC的角平分线与∠ACB的角平分线交于点P,若点P到边BC的距离为1,△ABC的周长为12,则△ABC的面积为( )
A.6 B.7 C.8 D.9
8.如图,∠AOB是一钢架,∠AOB=18°,为使钢架更加牢固,需在其内部添加一些钢管EF,FG,GH,…,添加的钢管长度都与OE的长度相等,则最多能添加的钢管根数为( )
A.4 B.5 C.6 D.无数
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠BCD,AD过点P,且与AB垂直,若BP=5,CP=12,则AD的长为( )
A.12 B.13 C. D.
10.如图,在△ABC中,∠BAC=90°,高AD与角平分线BE相交于点F,∠DAC的平分线AG分别交BC、BE于点G、O,连接FG,下列结论:①∠ABD=∠DAC;②∠AFE=∠AEF;③AG⊥EF;④FG∥AC,其中所有正确结论的序号是( )
A.①② B.①③ C.①②③ D.①②③④
11.如图,Rt△ABC中,∠C=90°,∠A=38°,点D在AB上,且点D与点B关于直线l对称,则∠ACD的度数为( )
A.10° B.14° C.38° D.52°
12.等腰三角形一腰上的高与另一腰的夹角为54°,则该等腰三角形底角的度数为( )
A.72° B.72°或36° C.36° D.72°或18°
13.如图,在△ABC中,AB=AC,∠A=36°,BD,CE分别平分∠ABC,∠ACB.若CD=5.则CE等于( )
A.4 B.4.5 C.5 D.5.5
14.如图,在△ABC中,分别以点B和点C为圆心,大于BC长为半径画弧,两弧相交于点M,N.作直线MN,交AC于点D,交BC于点E,连接BD.若AB=7,AC=12,BC=6,则△ABD的周长为( )
A.25 B.22 C.19 D.18
15.下列图案中,是轴对称图形的是( )
A. B. C. D.
16.如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F,若AB=5,AC=8,BC=10,则△AEF的周长为( )
A.5 B.8 C.10 D.13
17.如图,点C为BD上一点,AB=AC,AE=CE,AE∥BD,∠E=30°,则∠BAC的度数是( )
A.25° B.30° C.45° D.50°
18.如图,将△ABD沿△ABC的角平分线AD翻折,点B恰好落在AC边上的点E处.已知∠C=20°,AB+BD=AC,那么∠B的度数为( )
A.30° B.40° C.60° D.80°
19.如图,在三角形ABC中,∠C=60°,∠B=30°,D是BC上一点,将三角形ABD沿AD翻折后得到三角形AED,边AE交射线BC于点F,若DE∥AC,则∠BDA=( )
A.120° B.135° C.110° D.150°
20.如图,将△ABC沿AC所在的直线翻折得到△AB'C,再将△AB′C沿AB'所在的直线翻折得到△AB'C',点B,B',C'在同一条直线上,∠BAC=α,由此给出下列说法:①△ABC≌△AB′C′.②AC⊥BB'.③∠CB′B=2α.其中正确的说法是( )
A.①② B.①③ C.②③ D.①②③
参考答案
1.解:∵BD=AD,
∴∠ABD=∠A.
∵BD平分∠ABC,
∴∠ABD=∠CBD=.
∴∠A=.
∵∠ABC=∠C,
∴.
∴∠ABC=72°.
故选:C.
2.解:作DE⊥AB于E.
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=CD=3.
∴△ABD的面积为 ×3×10=15.
故选:C.
3.解:∵DE垂直平分BC,
∴DB=DC,
∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=5+7=12,
故选:B.
4.解:∵DE是AB边的垂直平分线,
∴EA=EB,
∵△BCE的周长等于45,
∴BC+CE+BE=BC+CE+EA=BC+AC=45,
∵AC=27,
∴BC=45﹣27=18,
故选:C.
5.解:连接AD并延长至E,
∵点D是△ABC三边垂直平分线的交点,
∴DA=DB,DA=DC,
∴∠DAB=∠DBA,∠DAC=∠DCA,
∴∠DAB=∠BDE,∠DAC=∠CDE,
∴∠BAC=∠BDC=×116°=58°,
故选:B.
6.解:当x=4时,4+4<10,不符合三角形三边关系,舍去;
当x=10时,4+10>10,符合三角形三边关系.
故选:B.
7.解:过点P作PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,如图所示:
∵∠ABC的角平分线与∠ACB的角平分线交于点P,
∴PD=PE=PF,
∵点P到边BC的距离为1,
∴PF=1,
∴PD=PE=1,
∵△ABC的周长为12,
∴△ABC的面积=
=
=6,
故选:A.
8.解:∵添加的钢管长度都与OE相等,∠AOB=18°,
∴∠GEF=∠FGE=36°,…从图中我们会发现有好几个等腰三角形,即第一个等腰三角形的底角是18°,第二个是36°,第三个是54°,四个是72°,五个是90°就不存在了.
所以一共有4个.
故选:A.
9.解:过P点作PH⊥BC于H,如图,
∵AB∥CD,AD⊥AB,
∴AD⊥CD,∠ABC+∠DCB=180°,
∵BP和CP分别平分∠ABC和∠BCD,
∴PH=PA=PD,∠PCB=∠DCB,∠PBC=∠ABC,
∴∠PBC+∠PCB=(∠ABC+∠DCB)=×180°=90°,
∴∠BPC=90°,
∴BC===13,
∵PH BC=PB PC,
∴PH==,
∴PA=PD=PH=,
∴AD=2PA=.
故选:D.
10.解:∵AD为高,
∴∠ADB=90°,
∵∠BAD+∠ABD=90°,∠BAD+∠DAC=90°,
∴∠ABD=∠DAC,所以①正确;
∵∠ABD+∠C=90°,
∴∠BAD=∠C,
∵∠AFE=∠ABF+∠BAF,∠AEF=∠C+∠EAC,
∴∠AFE=∠AEF,所以②正确;
∴AE=AF,
∵AG平分∠DAC,
∴AO⊥EF,所以③正确;
∵BO平分∠ABG,
∴∠ABO=∠GBO,
∵BO⊥AG,
∴∠BAO=∠BGO,
∴BA=BG,
∴OA=OG,
∴BO垂直平分AG,
∴FA=FG,
∴∠FAO=∠FGO,
∵∠FAO=∠EAO,
∴∠EAO=∠FGO,
∴FG∥AC,所以④正确.
故选:D.
11.解:∵∠C=90°,∠A=38°,
∴∠B=52°,
∵点D与点B关于直线l对称,
∴∠CDB=∠B=52°,
∵∠CDB=∠ACD+∠A,
∴52°=∠ACD+38°,
∴∠ACD=14°,
故选:B.
12.解:在等腰△ABC中,AB=AC,BD为腰AC上的高,∠ABD=54°,
当BD在△ABC内部时,如图1,
∵BD为高,
∴∠ADB=90°,
∴∠BAD=90°﹣54°=36°,
∵AB=AC,
∴∠ABC=∠ACB=(180°﹣36°)=72°;
当BD在△ABC外部时,如图2,
∵BD为高,
∴∠ADB=90°,
∴∠BAD=90°﹣54°=36°,
∵AB=AC,
∴∠ABC=∠ACB,
而∠BAD=∠ABC+∠ACB,
∴∠ACB=∠BAD=18°,
综上所述,这个等腰三角形底角的度数为72°或18°.
故选:D.
13.解:∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°,
∵BD,CE分别平分∠ABC,∠ACB,
∴∠DBC=∠ACE=36°,
∴∠BDC=180°﹣36°﹣72°=72°,
∴∠CED=180°﹣∠ACE﹣∠BDC=72°,
∴∠CED=∠CDE,
∴CE=CD=5,
故选:C.
14.解:由题意可得,
MN垂直平分BC,
∴DB=DC,
∵△ABD的周长是AB+BD+AD,
∴AB+BD+AD=AB+DC+AD=AB+AC,
∵AB=7,AC=12,
∴AB+AC=19,
∴∵△ABD的周长是19,
故选:C.
15.解:A.是轴对称图形,故此选项符合题意;
B.不是轴对称图形,故此选项不符合题意;
C.不是轴对称图形,故此选项不符合题意;
D.不是轴对称图形,故此选项不符合题意;
故选:A.
16.解:∵EG是线段AB的垂直平分线,
∴EA=EB,
同理,FA=FC,
∴△AEF的周长=EA+EF+FA=EB+EF+FC=BC=10,
故选:C.
17.解:∵AE=CE,∠E=30°,
∴△ACE中,∠CAE=75°,
∵AE∥BD,
∴∠ACB=∠CAE=75°,
∵AB=AC,
∴∠B=∠ACB=75°,
∴△ABC中,∠BAC=180°﹣75°×2=30°,
故选:B.
18.解:由翻折可得AB=AE,BD=DE,∠B=∠AED,
∵AB+BD=AC,AC=AE+CE=AB+CE,
∴BD=CE,
∴DE=CE,
∴∠C=∠EDC,
∵∠C=20°,
∴∠EDC=20°,
∴∠AED=∠C+∠EDC=40°,
∴∠B=40°.
故选:B.
19.解:∵∠C=60°,∠B=30°,
∵∠BAC=90°,
由折叠性质可得:
∠E=∠B=30°,∠BAD=∠EAD,
∵DE∥AC,
∴∠CAE=∠E=30°,
∴∠BAE=∠BAC﹣∠CAE=60°,
∴∠BAD=∠EAD=30°,
∴∠BDA=180°﹣∠B﹣∠BAD=120°,
故选:A.
20.解:①由翻折可知:△ABC≌△AB′C,△AB′C≌△AB′C′,
∴△ABC≌△AB′C′;故①正确;
②由翻折可知:点B与点B′关于AC对称,
∴AC⊥BB';故②正确;
③由翻折可知:∠B′AC′=∠B′AC=∠BAC=α,∠AB′C′=∠AB′C,
∴∠AB′B=90°﹣∠B′AC=90°﹣α,
∴∠AB′C′=180°﹣∠AB′B=180°﹣(90°﹣α)=90°+α,
∴∠AB′C=90°+α,
∴∠CB′B=∠AB′C﹣∠AB′B=90°+α﹣(90°﹣α)=2α,
∴∠CB′B=2α.故③正确.
综上所述:正确的说法是:①②③.
故选:D.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
