2022-2023学年北师大版九年级数学上册1.2矩形的性质与判定 同步达标测试题(word,含答案)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学上册1.2矩形的性质与判定 同步达标测试题(word,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 433.1KB | ||
| 资源类型 | 教案 | ||
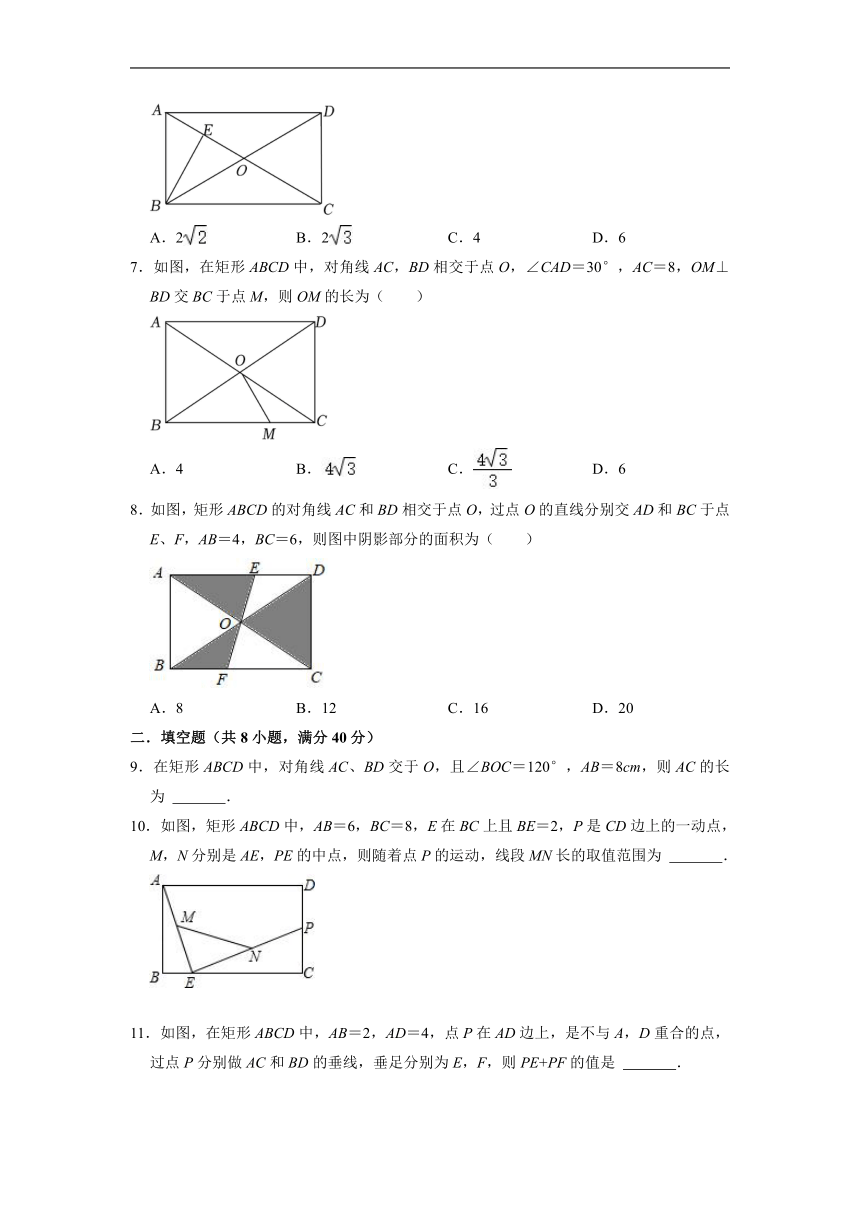
| 版本资源 | 北师大版 | ||
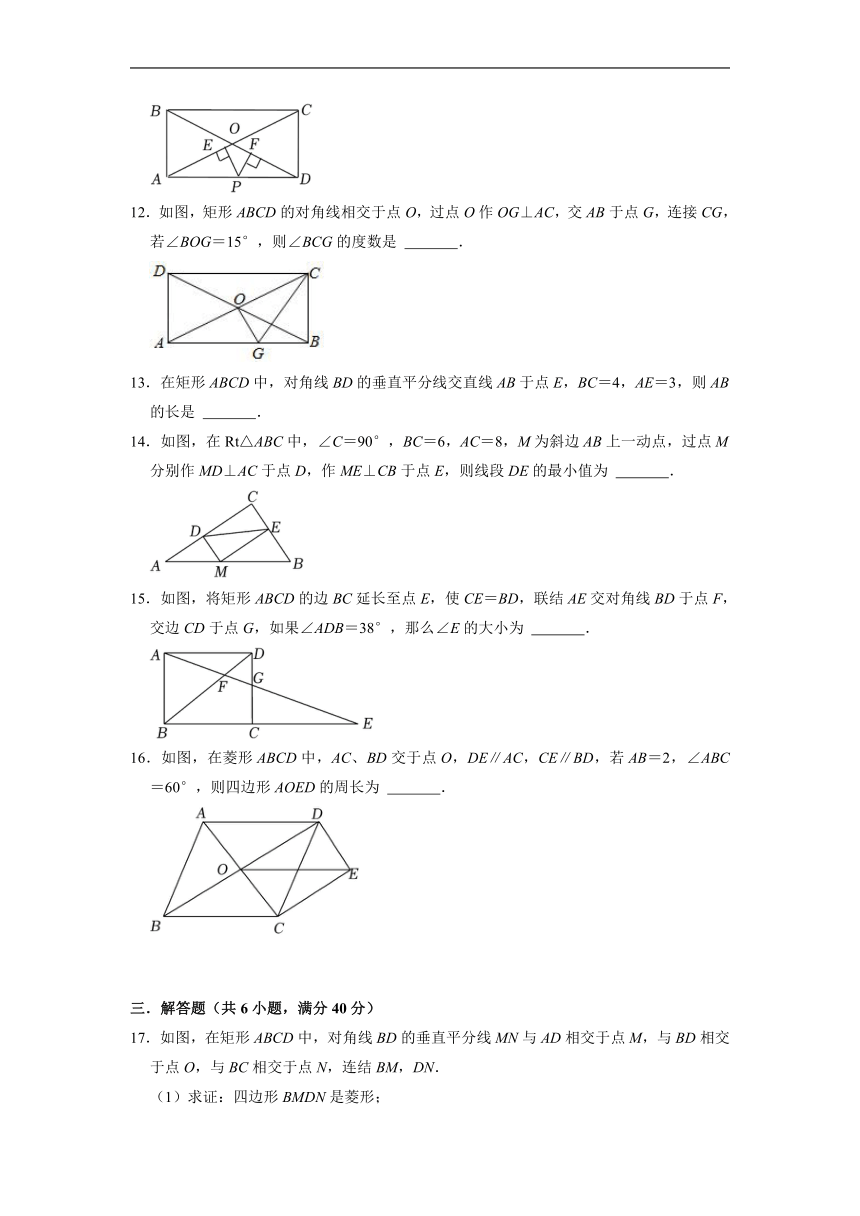
| 科目 | 数学 | ||
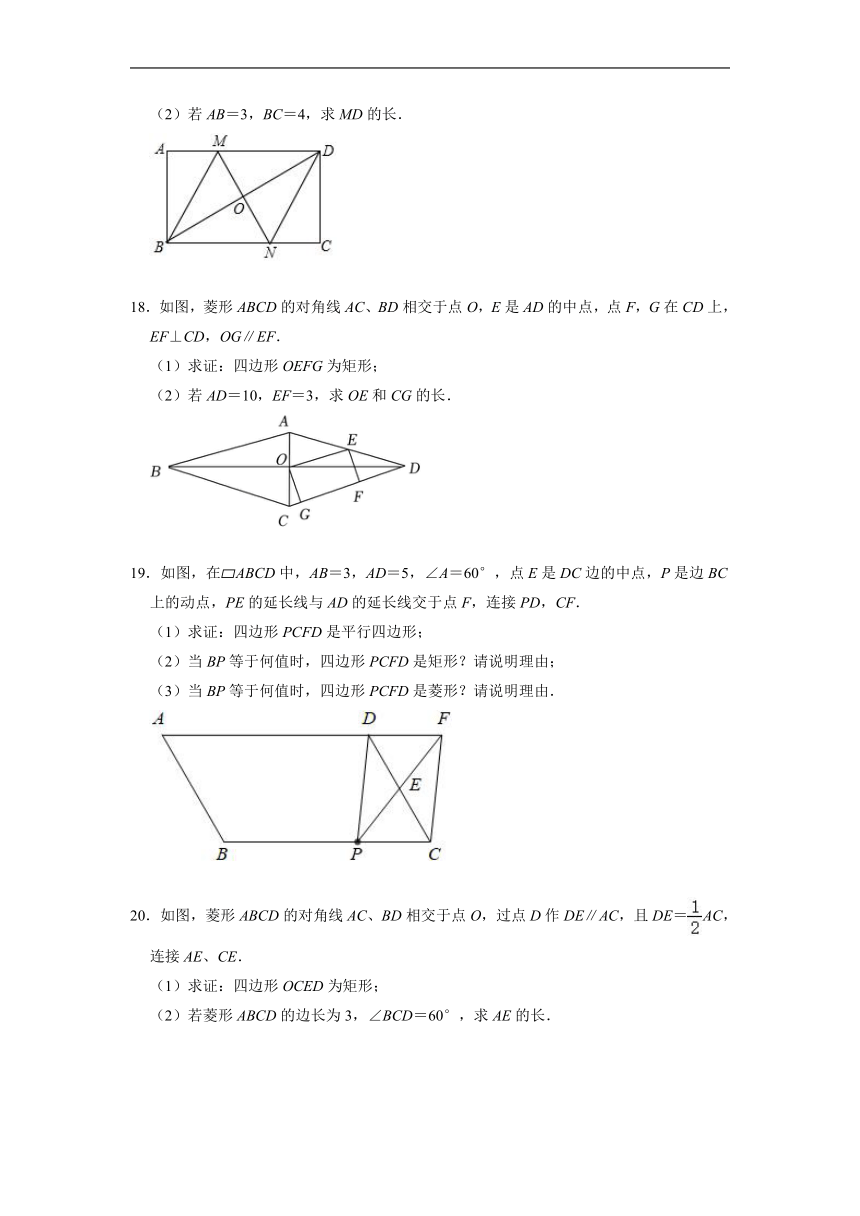
| 更新时间 | 2022-08-09 20:50:07 | ||
图片预览


文档简介
2022-2023学年北师大版九年级数学上册《1.2矩形的性质与判定》
同步达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.下列语句中,不是属于矩形性质的是( )
A.两条对角线互相平分 B.两条对角线相等
C.四个内角都是直角 D.两条对角线互相垂直
2.如图矩形ABCD中,对角线AC、BD交于点O,AB=3,∠BOC=120°,则BC=( )
A.4 B.5 C.6 D.
3.如图,矩形4BCD中,AC、BD交于点O,M、N分别为BC、OC的中点,若∠ACB=30°,AB=10,则MN的长为( )
A.5 B.5 C.5 D.4
4.如图,矩形ABCD中,AD=3,AB=4,M为线段BD上一动点,MP⊥CD于点P,MQ⊥BC于点Q,则PQ的最小值是( )
A. B.3 C. D.
5.如图,在矩形ABCD中,AB=3,BC=4,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE的长是( )
A. B. C.1 D.
6.如图,在矩形ABCD中,对角线AC,BD相交于点O,BE⊥AC于点E,若OC=4,AE=2,则边AB的长是( )
A.2 B.2 C.4 D.6
7.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠CAD=30°,AC=8,OM⊥BD交BC于点M,则OM的长为( )
A.4 B. C. D.6
8.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=4,BC=6,则图中阴影部分的面积为( )
A.8 B.12 C.16 D.20
二.填空题(共8小题,满分40分)
9.在矩形ABCD中,对角线AC、BD交于O,且∠BOC=120°,AB=8cm,则AC的长为 .
10.如图,矩形ABCD中,AB=6,BC=8,E在BC上且BE=2,P是CD边上的一动点,M,N分别是AE,PE的中点,则随着点P的运动,线段MN长的取值范围为 .
11.如图,在矩形ABCD中,AB=2,AD=4,点P在AD边上,是不与A,D重合的点,过点P分别做AC和BD的垂线,垂足分别为E,F,则PE+PF的值是 .
12.如图,矩形ABCD的对角线相交于点O,过点O作OG⊥AC,交AB于点G,连接CG,若∠BOG=15°,则∠BCG的度数是 .
13.在矩形ABCD中,对角线BD的垂直平分线交直线AB于点E,BC=4,AE=3,则AB的长是 .
14.如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,M为斜边AB上一动点,过点M分别作MD⊥AC于点D,作ME⊥CB于点E,则线段DE的最小值为 .
15.如图,将矩形ABCD的边BC延长至点E,使CE=BD,联结AE交对角线BD于点F,交边CD于点G,如果∠ADB=38°,那么∠E的大小为 .
16.如图,在菱形ABCD中,AC、BD交于点O,DE∥AC,CE∥BD,若AB=2,∠ABC=60°,则四边形AOED的周长为 .
三.解答题(共6小题,满分40分)
17.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连结BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=3,BC=4,求MD的长.
18.如图,菱形ABCD的对角线AC、BD相交于点O,E是AD的中点,点F,G在CD上,EF⊥CD,OG∥EF.
(1)求证:四边形OEFG为矩形;
(2)若AD=10,EF=3,求OE和CG的长.
19.如图,在 ABCD中,AB=3,AD=5,∠A=60°,点E是DC边的中点,P是边BC上的动点,PE的延长线与AD的延长线交于点F,连接PD,CF.
(1)求证:四边形PCFD是平行四边形;
(2)当BP等于何值时,四边形PCFD是矩形?请说明理由;
(3)当BP等于何值时,四边形PCFD是菱形?请说明理由.
20.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=AC,连接AE、CE.
(1)求证:四边形OCED为矩形;
(2)若菱形ABCD的边长为3,∠BCD=60°,求AE的长.
21.如图,在平行四边形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形ADFE是矩形;
(2)连接OF,若AD=6,EC=4,∠ABF=60°,求OF的长度.
22.如图,在△ABC中,点D是BC边的中点,点E是AD的中点,延长CE至F点,使得CE=FE,连接AF、BF.
(1)求证:四边形AFBD是平行四边形;
(2)当AB=AC时,求证:四边形AFBD是矩形.
参考答案
一.选择题(共8小题,满分40分)
1.解:A、矩形的对角线互相平分,故本选项不符合题意;
B、矩形的对角线相等,故本选项不符合题意;
C、矩形的四个角都是直角,故本选项不符合题意;
D、菱形的对角线互相垂直,故本选项符合题意.
故选:D.
2.解:∵四边形ABCD是矩形,
∴∠ABC=90°,OA=OB=OC,
∵∠BOC=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=3,
∴AC=2OA=6,
∴BC=.
故选:D.
3.解:∵四边形ABCD是矩形,
∴AC=BD,AO=OC,OB=OD,
∴AO=BO,∠AOB=∠ACB+∠OBC=30°+30°=60°,
∴△ABO是等边三角形,
∴OB=AB=10,
∵M、N分别为BC、OC的中点,
∴MN是△BOC的中位线,
∴MN=OB=5,
故选:B.
4.解:如图,连接CM,
∵MP⊥CD于点P,MQ⊥BC于点Q,
∴∠CPM=∠CQM=90°,
∵四边形ABCD是矩形,
∴BC=AD=3,CD=AB=4,∠BCD=90°,
∴四边形PCQM是矩形,
∴PQ=CM,
由勾股定理得:BD===5,
当CM⊥BD时,CM最小,则PQ最小,
此时,S△BCD=BD CM=BC CD,
∴CM===,
∴PQ的最小值为,
故选:A.
5.解:连接CE,如图所示:
∵四边形ABCD是矩形,
∴∠ADC=90°,CD=AB=3,AD=BC=4,OA=OC,
∵EF⊥AC,
∴AE=CE,
设DE=x,则CE=AE=4﹣x,
在Rt△CDE中,由勾股定理得:x2+32=(4﹣x)2,
解得:x=,
即DE=.
故选:A.
6.解:∵四边形ABCD是矩形,
∴AO=BO=CO=4,
∵AE=2,
∴AE=EO=2,
∵BE⊥AC,
∴AB=BO=4,
故选:C.
7.解:如图:连接DM
∵矩形ABCD中,对角线AC,BD相交于点O,
∴OA=OB=OC=OD,AD=BC,∠BCD=∠ADC=90°.
∵∠CAD=30°,
∴CD=AC=4,AD=BC=4,
∵矩形ABCD中,AD∥BC,
∴∠OCM=∠CAD=30°=∠OBC,
∴∠BOC=120°
∵OM⊥BD,
∴BM=DM,∠BOM=90°,
∴∠MOC=120°﹣90°=30°,∠BDM=∠CBO=30°,
∴OM=CM.
∵∠DMC是△BMD的外角,
∴∠DMC=30°+30°=60°.
∴DC=CM.
∴CM==.
∴OM=.
故选:C.
8.解:∵四边形ABCD是矩形,
∴OA=OC,∠AEO=∠CFO;
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴S△AOE=S△COF,
∴S阴影=S△AOE+S△BOF+S△COD=S△AOE+S△BOF+S△COD=S△BCD;
∵S△BCD=BC CD=12,故S阴影=12.
故选:B.
二.填空题(共8小题,满分40分)
9.解:∵四边形ABCD为矩形,
∴∠ABC=90°,OA=BO=OC=DO,
∴∠OBC=∠OCB,
∵∠BOC=120°,
∴∠OCB=30°,
∴AC=2AB=2×8=16cm.
故答案为:16cm.
10.解:连接AP,AC,
在矩形ABCD中,AB=6,BC=8,
由勾股定理得AC=10,
∵点P在CD上运动,
∴8≤AP≤10,
∵M,N分别是AE,PE的中点,
∴MN是△AEP的中位线,
∴MN=AP,
∴4≤MN≤5,
故答案为:4≤MN≤5.
11.解:如图所示,连接OP,
∵AB=2,AD=4,
由勾股定理可得BD==2,S△ABD=AB AD=×2×4=4,
在矩形ABCD中,OA=OD=OB=BD=,
∵S△AOD=S△AOP+S△DOP=S△ABD,
∴ OA PE+ OD PF=×4=2,
∴PE+PF=,
故答案为:.
12.解:∵四边形ABCD是矩形,
∴∠ABC=90°,BD=AC,AO=OC,BO=OD,
∴OC=OB,
∴∠OCB=∠OBC,
∵AO=OC,OG⊥AC,
∴GA=GC,∠GOC=90°,
∵∠BOG=15°,
∴∠COB=90°﹣15°=75°,
∴∠OCB=∠OBC=×(180°﹣∠COB)=52.5°,
∴∠CAB=180°﹣∠ABC﹣∠OCB=180°﹣90°﹣52.5°=37.5°,
∴∠ACG=37.5°,
∴∠BCG=∠OCB﹣∠ACG=52.5°﹣37.5°=15°,
故答案为:15°.
13.解:分两种情况:
①当点E在AD的上方时,如图,
则AE=3,AD=BC=4,
∵∠EAD=90°,
∴DE===5,
∵OE是线段BD的垂直平分线,
∴BE=DE=5,
∴AB=BE﹣AE=2;
②当点E在AD的下方时,如图,
则AE=3,AD=BC=4,
∵∠EAD=90°,
∴DE===5,
∵OE是线段BD的垂直平分线,
∴BE=DE=5,
∴AB=AE+BE=8;
综上所述,AB的长为2或8,
故答案为:2或8.
14.解:连接CM,如图所示:
∵MD⊥AC,ME⊥CB,
∴∠MDC=∠MEC=90°,
∵∠ACB=90°,
∴四边形CDME是矩形,
∴DE=CM,
∵∠C=90°,BC=6,AC=8,
∴AB==10,
当CM⊥AB时,CM最短,此时△ABC的面积=AB CM=BC AC,
∴CM的最小值===,
∴线段DE的最小值为,
故答案为:.
15.解:连接AC交BD于O,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠OBC,
∵∠ADB=38°,
∴∠OBC=38°,
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OB=OC,
∴∠OCB=∠OBC=38°,
∵CE=BD,AC=BD,
AC=CE,
∴∠E=∠CAE,
∵∠E+CAE=OCB=38°,
∴E=38°=19°,
故答案为:19°.
16.解:∵DE∥AC,CE∥BD,
∴四边形ODEC是平行四边形,
∵四边形ABCD是菱形,
∴AD=AB=BC=2,OA=OC,AC⊥BD,
∴∠COD=90°,
∴平行四边形ODEC是矩形,
∴DE=OC,
∴DE=OA,
又∵DE∥AC,
∴四边形AOED是平行四边形,
∴AD=OE,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=2,
∴DE=OA=AC=1,
∴平行四边形AOED的周长=2(AD+OA)=2×(2+1)=6,
故答案为:6.
三.解答题(共6小题,满分40分)
17.解:(1)∵MN是BD的垂直平分线,
∴MB=MD,∠MOD=∠BON=90°,OB=OD.
∵四边形ABCD是矩形,
∴∠A=90°,AD∥MC.
∴∠1=∠2.
在△MOD和△NOB中
,
∴△MOD≌△NOB(ASA).
∴OM=ON.
∵OB=OD,
∴四边形MBND是平行四边形.
∵MB=MD,
∴四边形MBND是菱形.
(2)设MD=MB=x,则AM=AD﹣MD=4﹣x.
∵AM2=BM2﹣AM2,
∴32=x2﹣(4﹣x)2.
解得x=.
∴MD的长为.
18.(1)证明:∵点 O 为菱形 ABCD 对角线 AC、BD 的交点,点 E 为边AD的中点,
∴OE∥CD,
∴OE∥GF,
∵OG∥EF,
∴四边形OGFE为平行四边形,
又EF⊥DC,
∴∠EFG=90°,
∴四边形OGFE为矩形;
(2)解:∵AD=10,EF=3,
∴CD=AD=10,
∴OE=GF=AD=5,
∵四边形ABCD为菱形,点E为BC中点,
∴DE=AD=5,
在Rt△EFD中,FD==4,
∴CG=CD﹣GF﹣DF=10﹣5﹣4=1.
19.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DFE=∠CPE,
∵E是CD的中点,
∴CE=DE,
在△DFE和△CPE中,
,
∴△DFE≌△CPE(ASA),
∴FE=PE,
∴四边形PCFD是平行四边形;
(2)解:当BP=3.5时,平行四边形CEDF是矩形,理由如下:
如图,过B作BM⊥AD于M,
∵∠A=60°,AB=3,
∴AM=AB=1.5,
∵四边形ABCD是平行四边形,
∴∠BCD=∠A=60°,DC=AB=3,BC=AD=5,
∵AE=3.5,
∴CP=1.5=AM,
在△MBA和△PDC中,
,
∴△MBA≌△PDC(SAS),
∴∠DPC=∠BMA=90°,
∵四边形PCFD是平行四边形,
∴平行四边形PCFD是矩形,
故答案为:3.5;
(3)解:当BP=2时,四边形PCFD是菱形,理由如下:
∵BC=5,BP=2,
∴CP=3,
∵CD=3,∠DCP=∠A=60°,
∴△DCP是等边三角形,
∴DP=CP,
∵四边形PCFD是平行四边形,
∴平行四边形PCFD是菱形.
20.(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,AO=OC=AC,
∴∠DOC=90°,
∵DE∥AC,DE=AC,
∴DE=OC,DE∥OC,
∴四边形OCED是平行四边形,
又∵∠DOC=90°,
∴平行四边形OCED是矩形;
(2)解:∵四边形ABCD是菱形,
∴AC⊥BD,BC=CD=8,OB=OD,AO=OC=AC,
∵∠BCD=60°,
∴△BCD是等边三角形,
∴BD=BC=3,
∴OD=OB=,
∴OC=,
∴AC=2OC=3,
由(1)得:四边形OCED为矩形,
∴CE=OD=1,∠OCE=90°,
在Rt△ACE中,由勾股定理得:AE==,
故AE的长为:.
21.(1)证明:∵在平行四边形ABCD中,
∴AB∥DC且AB=DC,
∴∠ABE=∠DCF,
在△ABE和△DCF中,,
∴△ABE≌△DCF(SAS),
∴AE=DF,∠AEB=∠DFC=90°,
∴AE∥DF,
∴四边形ADFE是矩形;
(2)解:由(1)知:四边形ADFE是矩形,
∴EF=AD=6,
∵EC=4,
∴BE=CF=2,
∴BF=8,
Rt△ABE中,∠ABE=60°,
∴AB=2BE=4,
∴DF=AE=,
∴BD==2,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OF=BD=.
22.(1)证明:∵点E是AD的中点,
∴AE=DE,
∵∠AEF=∠DEC,CE=FE,
∴△AFE≌△DCE(SAS),
∴AF=CD,∠AFE=∠DCE,
∴AF∥CD,
∵点D是BC边的中点,
∴BD=CD,
∴AF=BD,
∴四边形AFBD是平行四边形;
(2)证明:∵AB=AC,BD=DC,
∴AD⊥BC.
∴∠ADB=90°.
∵四边形AFBD是平行四边形,
∴四边形AFBD是矩形.
同步达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.下列语句中,不是属于矩形性质的是( )
A.两条对角线互相平分 B.两条对角线相等
C.四个内角都是直角 D.两条对角线互相垂直
2.如图矩形ABCD中,对角线AC、BD交于点O,AB=3,∠BOC=120°,则BC=( )
A.4 B.5 C.6 D.
3.如图,矩形4BCD中,AC、BD交于点O,M、N分别为BC、OC的中点,若∠ACB=30°,AB=10,则MN的长为( )
A.5 B.5 C.5 D.4
4.如图,矩形ABCD中,AD=3,AB=4,M为线段BD上一动点,MP⊥CD于点P,MQ⊥BC于点Q,则PQ的最小值是( )
A. B.3 C. D.
5.如图,在矩形ABCD中,AB=3,BC=4,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE的长是( )
A. B. C.1 D.
6.如图,在矩形ABCD中,对角线AC,BD相交于点O,BE⊥AC于点E,若OC=4,AE=2,则边AB的长是( )
A.2 B.2 C.4 D.6
7.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠CAD=30°,AC=8,OM⊥BD交BC于点M,则OM的长为( )
A.4 B. C. D.6
8.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=4,BC=6,则图中阴影部分的面积为( )
A.8 B.12 C.16 D.20
二.填空题(共8小题,满分40分)
9.在矩形ABCD中,对角线AC、BD交于O,且∠BOC=120°,AB=8cm,则AC的长为 .
10.如图,矩形ABCD中,AB=6,BC=8,E在BC上且BE=2,P是CD边上的一动点,M,N分别是AE,PE的中点,则随着点P的运动,线段MN长的取值范围为 .
11.如图,在矩形ABCD中,AB=2,AD=4,点P在AD边上,是不与A,D重合的点,过点P分别做AC和BD的垂线,垂足分别为E,F,则PE+PF的值是 .
12.如图,矩形ABCD的对角线相交于点O,过点O作OG⊥AC,交AB于点G,连接CG,若∠BOG=15°,则∠BCG的度数是 .
13.在矩形ABCD中,对角线BD的垂直平分线交直线AB于点E,BC=4,AE=3,则AB的长是 .
14.如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,M为斜边AB上一动点,过点M分别作MD⊥AC于点D,作ME⊥CB于点E,则线段DE的最小值为 .
15.如图,将矩形ABCD的边BC延长至点E,使CE=BD,联结AE交对角线BD于点F,交边CD于点G,如果∠ADB=38°,那么∠E的大小为 .
16.如图,在菱形ABCD中,AC、BD交于点O,DE∥AC,CE∥BD,若AB=2,∠ABC=60°,则四边形AOED的周长为 .
三.解答题(共6小题,满分40分)
17.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连结BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=3,BC=4,求MD的长.
18.如图,菱形ABCD的对角线AC、BD相交于点O,E是AD的中点,点F,G在CD上,EF⊥CD,OG∥EF.
(1)求证:四边形OEFG为矩形;
(2)若AD=10,EF=3,求OE和CG的长.
19.如图,在 ABCD中,AB=3,AD=5,∠A=60°,点E是DC边的中点,P是边BC上的动点,PE的延长线与AD的延长线交于点F,连接PD,CF.
(1)求证:四边形PCFD是平行四边形;
(2)当BP等于何值时,四边形PCFD是矩形?请说明理由;
(3)当BP等于何值时,四边形PCFD是菱形?请说明理由.
20.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=AC,连接AE、CE.
(1)求证:四边形OCED为矩形;
(2)若菱形ABCD的边长为3,∠BCD=60°,求AE的长.
21.如图,在平行四边形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形ADFE是矩形;
(2)连接OF,若AD=6,EC=4,∠ABF=60°,求OF的长度.
22.如图,在△ABC中,点D是BC边的中点,点E是AD的中点,延长CE至F点,使得CE=FE,连接AF、BF.
(1)求证:四边形AFBD是平行四边形;
(2)当AB=AC时,求证:四边形AFBD是矩形.
参考答案
一.选择题(共8小题,满分40分)
1.解:A、矩形的对角线互相平分,故本选项不符合题意;
B、矩形的对角线相等,故本选项不符合题意;
C、矩形的四个角都是直角,故本选项不符合题意;
D、菱形的对角线互相垂直,故本选项符合题意.
故选:D.
2.解:∵四边形ABCD是矩形,
∴∠ABC=90°,OA=OB=OC,
∵∠BOC=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=3,
∴AC=2OA=6,
∴BC=.
故选:D.
3.解:∵四边形ABCD是矩形,
∴AC=BD,AO=OC,OB=OD,
∴AO=BO,∠AOB=∠ACB+∠OBC=30°+30°=60°,
∴△ABO是等边三角形,
∴OB=AB=10,
∵M、N分别为BC、OC的中点,
∴MN是△BOC的中位线,
∴MN=OB=5,
故选:B.
4.解:如图,连接CM,
∵MP⊥CD于点P,MQ⊥BC于点Q,
∴∠CPM=∠CQM=90°,
∵四边形ABCD是矩形,
∴BC=AD=3,CD=AB=4,∠BCD=90°,
∴四边形PCQM是矩形,
∴PQ=CM,
由勾股定理得:BD===5,
当CM⊥BD时,CM最小,则PQ最小,
此时,S△BCD=BD CM=BC CD,
∴CM===,
∴PQ的最小值为,
故选:A.
5.解:连接CE,如图所示:
∵四边形ABCD是矩形,
∴∠ADC=90°,CD=AB=3,AD=BC=4,OA=OC,
∵EF⊥AC,
∴AE=CE,
设DE=x,则CE=AE=4﹣x,
在Rt△CDE中,由勾股定理得:x2+32=(4﹣x)2,
解得:x=,
即DE=.
故选:A.
6.解:∵四边形ABCD是矩形,
∴AO=BO=CO=4,
∵AE=2,
∴AE=EO=2,
∵BE⊥AC,
∴AB=BO=4,
故选:C.
7.解:如图:连接DM
∵矩形ABCD中,对角线AC,BD相交于点O,
∴OA=OB=OC=OD,AD=BC,∠BCD=∠ADC=90°.
∵∠CAD=30°,
∴CD=AC=4,AD=BC=4,
∵矩形ABCD中,AD∥BC,
∴∠OCM=∠CAD=30°=∠OBC,
∴∠BOC=120°
∵OM⊥BD,
∴BM=DM,∠BOM=90°,
∴∠MOC=120°﹣90°=30°,∠BDM=∠CBO=30°,
∴OM=CM.
∵∠DMC是△BMD的外角,
∴∠DMC=30°+30°=60°.
∴DC=CM.
∴CM==.
∴OM=.
故选:C.
8.解:∵四边形ABCD是矩形,
∴OA=OC,∠AEO=∠CFO;
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴S△AOE=S△COF,
∴S阴影=S△AOE+S△BOF+S△COD=S△AOE+S△BOF+S△COD=S△BCD;
∵S△BCD=BC CD=12,故S阴影=12.
故选:B.
二.填空题(共8小题,满分40分)
9.解:∵四边形ABCD为矩形,
∴∠ABC=90°,OA=BO=OC=DO,
∴∠OBC=∠OCB,
∵∠BOC=120°,
∴∠OCB=30°,
∴AC=2AB=2×8=16cm.
故答案为:16cm.
10.解:连接AP,AC,
在矩形ABCD中,AB=6,BC=8,
由勾股定理得AC=10,
∵点P在CD上运动,
∴8≤AP≤10,
∵M,N分别是AE,PE的中点,
∴MN是△AEP的中位线,
∴MN=AP,
∴4≤MN≤5,
故答案为:4≤MN≤5.
11.解:如图所示,连接OP,
∵AB=2,AD=4,
由勾股定理可得BD==2,S△ABD=AB AD=×2×4=4,
在矩形ABCD中,OA=OD=OB=BD=,
∵S△AOD=S△AOP+S△DOP=S△ABD,
∴ OA PE+ OD PF=×4=2,
∴PE+PF=,
故答案为:.
12.解:∵四边形ABCD是矩形,
∴∠ABC=90°,BD=AC,AO=OC,BO=OD,
∴OC=OB,
∴∠OCB=∠OBC,
∵AO=OC,OG⊥AC,
∴GA=GC,∠GOC=90°,
∵∠BOG=15°,
∴∠COB=90°﹣15°=75°,
∴∠OCB=∠OBC=×(180°﹣∠COB)=52.5°,
∴∠CAB=180°﹣∠ABC﹣∠OCB=180°﹣90°﹣52.5°=37.5°,
∴∠ACG=37.5°,
∴∠BCG=∠OCB﹣∠ACG=52.5°﹣37.5°=15°,
故答案为:15°.
13.解:分两种情况:
①当点E在AD的上方时,如图,
则AE=3,AD=BC=4,
∵∠EAD=90°,
∴DE===5,
∵OE是线段BD的垂直平分线,
∴BE=DE=5,
∴AB=BE﹣AE=2;
②当点E在AD的下方时,如图,
则AE=3,AD=BC=4,
∵∠EAD=90°,
∴DE===5,
∵OE是线段BD的垂直平分线,
∴BE=DE=5,
∴AB=AE+BE=8;
综上所述,AB的长为2或8,
故答案为:2或8.
14.解:连接CM,如图所示:
∵MD⊥AC,ME⊥CB,
∴∠MDC=∠MEC=90°,
∵∠ACB=90°,
∴四边形CDME是矩形,
∴DE=CM,
∵∠C=90°,BC=6,AC=8,
∴AB==10,
当CM⊥AB时,CM最短,此时△ABC的面积=AB CM=BC AC,
∴CM的最小值===,
∴线段DE的最小值为,
故答案为:.
15.解:连接AC交BD于O,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠OBC,
∵∠ADB=38°,
∴∠OBC=38°,
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OB=OC,
∴∠OCB=∠OBC=38°,
∵CE=BD,AC=BD,
AC=CE,
∴∠E=∠CAE,
∵∠E+CAE=OCB=38°,
∴E=38°=19°,
故答案为:19°.
16.解:∵DE∥AC,CE∥BD,
∴四边形ODEC是平行四边形,
∵四边形ABCD是菱形,
∴AD=AB=BC=2,OA=OC,AC⊥BD,
∴∠COD=90°,
∴平行四边形ODEC是矩形,
∴DE=OC,
∴DE=OA,
又∵DE∥AC,
∴四边形AOED是平行四边形,
∴AD=OE,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=2,
∴DE=OA=AC=1,
∴平行四边形AOED的周长=2(AD+OA)=2×(2+1)=6,
故答案为:6.
三.解答题(共6小题,满分40分)
17.解:(1)∵MN是BD的垂直平分线,
∴MB=MD,∠MOD=∠BON=90°,OB=OD.
∵四边形ABCD是矩形,
∴∠A=90°,AD∥MC.
∴∠1=∠2.
在△MOD和△NOB中
,
∴△MOD≌△NOB(ASA).
∴OM=ON.
∵OB=OD,
∴四边形MBND是平行四边形.
∵MB=MD,
∴四边形MBND是菱形.
(2)设MD=MB=x,则AM=AD﹣MD=4﹣x.
∵AM2=BM2﹣AM2,
∴32=x2﹣(4﹣x)2.
解得x=.
∴MD的长为.
18.(1)证明:∵点 O 为菱形 ABCD 对角线 AC、BD 的交点,点 E 为边AD的中点,
∴OE∥CD,
∴OE∥GF,
∵OG∥EF,
∴四边形OGFE为平行四边形,
又EF⊥DC,
∴∠EFG=90°,
∴四边形OGFE为矩形;
(2)解:∵AD=10,EF=3,
∴CD=AD=10,
∴OE=GF=AD=5,
∵四边形ABCD为菱形,点E为BC中点,
∴DE=AD=5,
在Rt△EFD中,FD==4,
∴CG=CD﹣GF﹣DF=10﹣5﹣4=1.
19.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DFE=∠CPE,
∵E是CD的中点,
∴CE=DE,
在△DFE和△CPE中,
,
∴△DFE≌△CPE(ASA),
∴FE=PE,
∴四边形PCFD是平行四边形;
(2)解:当BP=3.5时,平行四边形CEDF是矩形,理由如下:
如图,过B作BM⊥AD于M,
∵∠A=60°,AB=3,
∴AM=AB=1.5,
∵四边形ABCD是平行四边形,
∴∠BCD=∠A=60°,DC=AB=3,BC=AD=5,
∵AE=3.5,
∴CP=1.5=AM,
在△MBA和△PDC中,
,
∴△MBA≌△PDC(SAS),
∴∠DPC=∠BMA=90°,
∵四边形PCFD是平行四边形,
∴平行四边形PCFD是矩形,
故答案为:3.5;
(3)解:当BP=2时,四边形PCFD是菱形,理由如下:
∵BC=5,BP=2,
∴CP=3,
∵CD=3,∠DCP=∠A=60°,
∴△DCP是等边三角形,
∴DP=CP,
∵四边形PCFD是平行四边形,
∴平行四边形PCFD是菱形.
20.(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,AO=OC=AC,
∴∠DOC=90°,
∵DE∥AC,DE=AC,
∴DE=OC,DE∥OC,
∴四边形OCED是平行四边形,
又∵∠DOC=90°,
∴平行四边形OCED是矩形;
(2)解:∵四边形ABCD是菱形,
∴AC⊥BD,BC=CD=8,OB=OD,AO=OC=AC,
∵∠BCD=60°,
∴△BCD是等边三角形,
∴BD=BC=3,
∴OD=OB=,
∴OC=,
∴AC=2OC=3,
由(1)得:四边形OCED为矩形,
∴CE=OD=1,∠OCE=90°,
在Rt△ACE中,由勾股定理得:AE==,
故AE的长为:.
21.(1)证明:∵在平行四边形ABCD中,
∴AB∥DC且AB=DC,
∴∠ABE=∠DCF,
在△ABE和△DCF中,,
∴△ABE≌△DCF(SAS),
∴AE=DF,∠AEB=∠DFC=90°,
∴AE∥DF,
∴四边形ADFE是矩形;
(2)解:由(1)知:四边形ADFE是矩形,
∴EF=AD=6,
∵EC=4,
∴BE=CF=2,
∴BF=8,
Rt△ABE中,∠ABE=60°,
∴AB=2BE=4,
∴DF=AE=,
∴BD==2,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OF=BD=.
22.(1)证明:∵点E是AD的中点,
∴AE=DE,
∵∠AEF=∠DEC,CE=FE,
∴△AFE≌△DCE(SAS),
∴AF=CD,∠AFE=∠DCE,
∴AF∥CD,
∵点D是BC边的中点,
∴BD=CD,
∴AF=BD,
∴四边形AFBD是平行四边形;
(2)证明:∵AB=AC,BD=DC,
∴AD⊥BC.
∴∠ADB=90°.
∵四边形AFBD是平行四边形,
∴四边形AFBD是矩形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
