23.1图形的旋转同步练习 2022-2023学年人教版数学九年级上册(Word版含答案)
文档属性
| 名称 | 23.1图形的旋转同步练习 2022-2023学年人教版数学九年级上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 487.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 08:44:00 | ||
图片预览


文档简介
23.1图形的旋转同步练习
一、单选题
1.下列现象中属于旋转的是( )
A.汽车在急刹车时向前滑动 B.拧开水龙头
C.雪橇在雪地里滑动 D.电梯的上升与下降
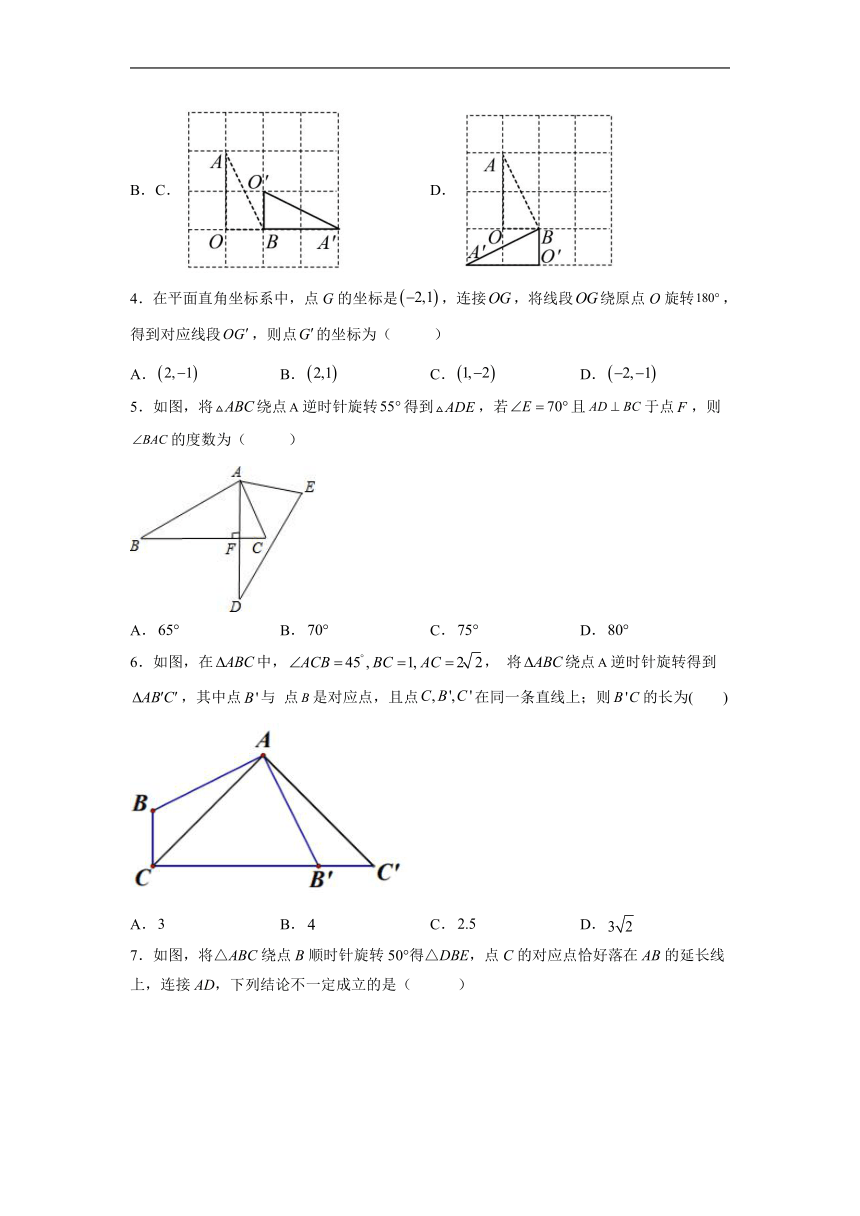
2.如图,在方格纸上建立的平面直角坐标系中,将绕点按顺时针方向旋转90°,得到,则点的坐标为( ).
A. B.
C. D.
3.如图,在方格纸中,将绕点按顺时针方向旋转90°后得到,则下列四个图形中正确的是( )
B.
C. D.
4.在平面直角坐标系中,点G的坐标是,连接,将线段绕原点O旋转,得到对应线段,则点的坐标为( )
A. B. C. D.
5.如图,将绕点逆时针旋转得到,若且于点,则的度数为( )
A. B. C. D.
6.如图,在中,, 将绕点逆时针旋转得到,其中点与 点是对应点,且点在同一条直线上;则的长为( )
A. B. C. D.
7.如图,将△ABC绕点B顺时针旋转50°得△DBE,点C的对应点恰好落在AB的延长线上,连接AD,下列结论不一定成立的是( )
A.AB=DB B.∠CBD=80° C.∠ABD=∠E D.△ABC≌△DBE
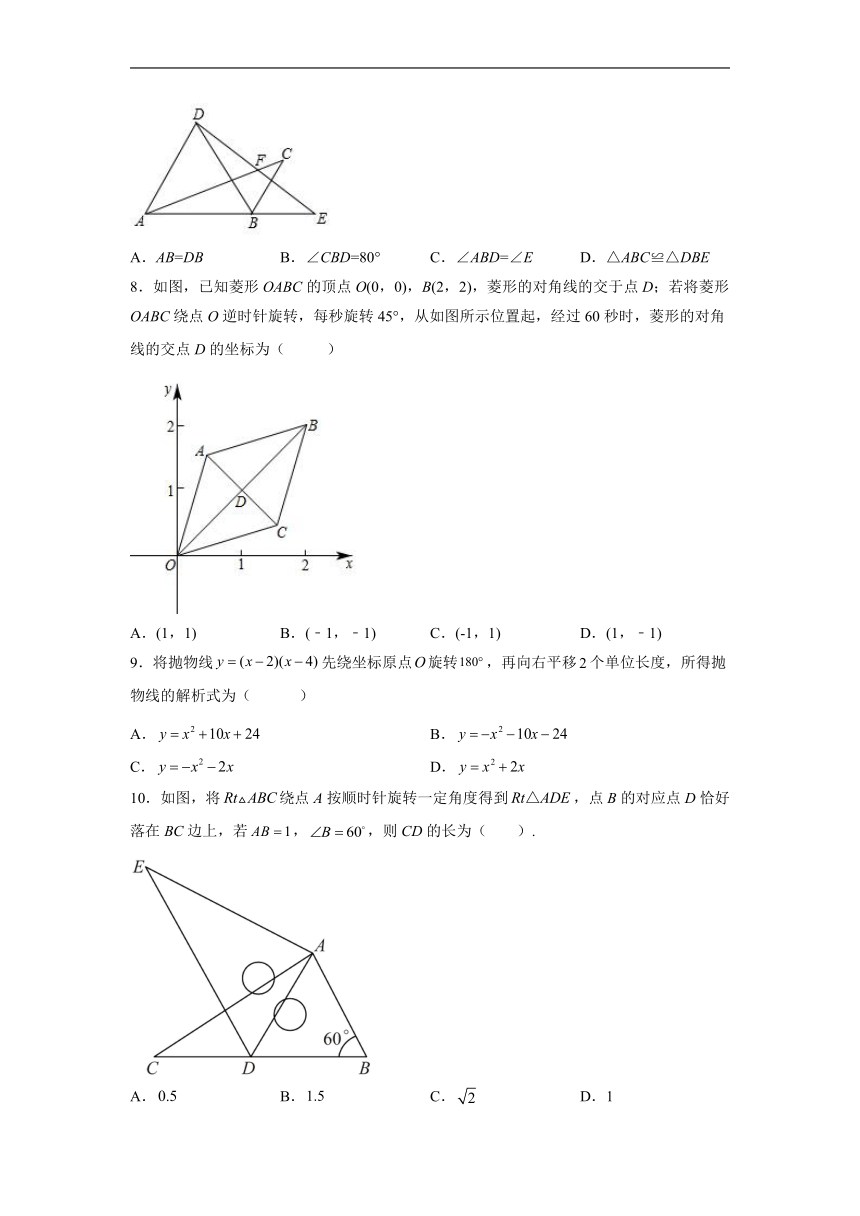
8.如图,已知菱形OABC的顶点O(0,0),B(2,2),菱形的对角线的交于点D;若将菱形OABC绕点O逆时针旋转,每秒旋转45°,从如图所示位置起,经过60秒时,菱形的对角线的交点D的坐标为( )
A.(1,1) B.(﹣1,﹣1) C.(-1,1) D.(1,﹣1)
9.将抛物线先绕坐标原点旋转,再向右平移个单位长度,所得抛物线的解析式为( )
A. B.
C. D.
10.如图,将绕点A按顺时针旋转一定角度得到,点B的对应点D恰好落在BC边上,若,,则CD的长为( ).
A. B. C. D.1
11.以原点为中心,将点P(4,5)按逆时针方向旋转90°,得到的点Q所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.如图,点A,B的坐标分别为(1,1)、(3,2),将△ABC绕点A按逆时针方向旋转90°,得到△A'B'C',则B'点的坐标为( )
A.(﹣1,3) B.(-1,2) C.(0,2) D.(0,3)
二、填空题
13.将数字“6”旋转,得到数字“9”,将数字“9”旋转,得到数字“6”,现将数字“689”整体旋转,得到的数字是______.
14.如图,将一个顶角为30°角的等腰△ABC绕点A顺时针旋转一个角度α(0<α<180°)得到△AB'C′,使得点B′、A、C在同一条直线上,则α等于_____°.
15.将正方形OEFG放在平面直角坐标系中,O是坐标原点,若点E的坐标为,则点G的坐标为_____.
16.如图,在中,,,,为内一点,则的最小值为__________.
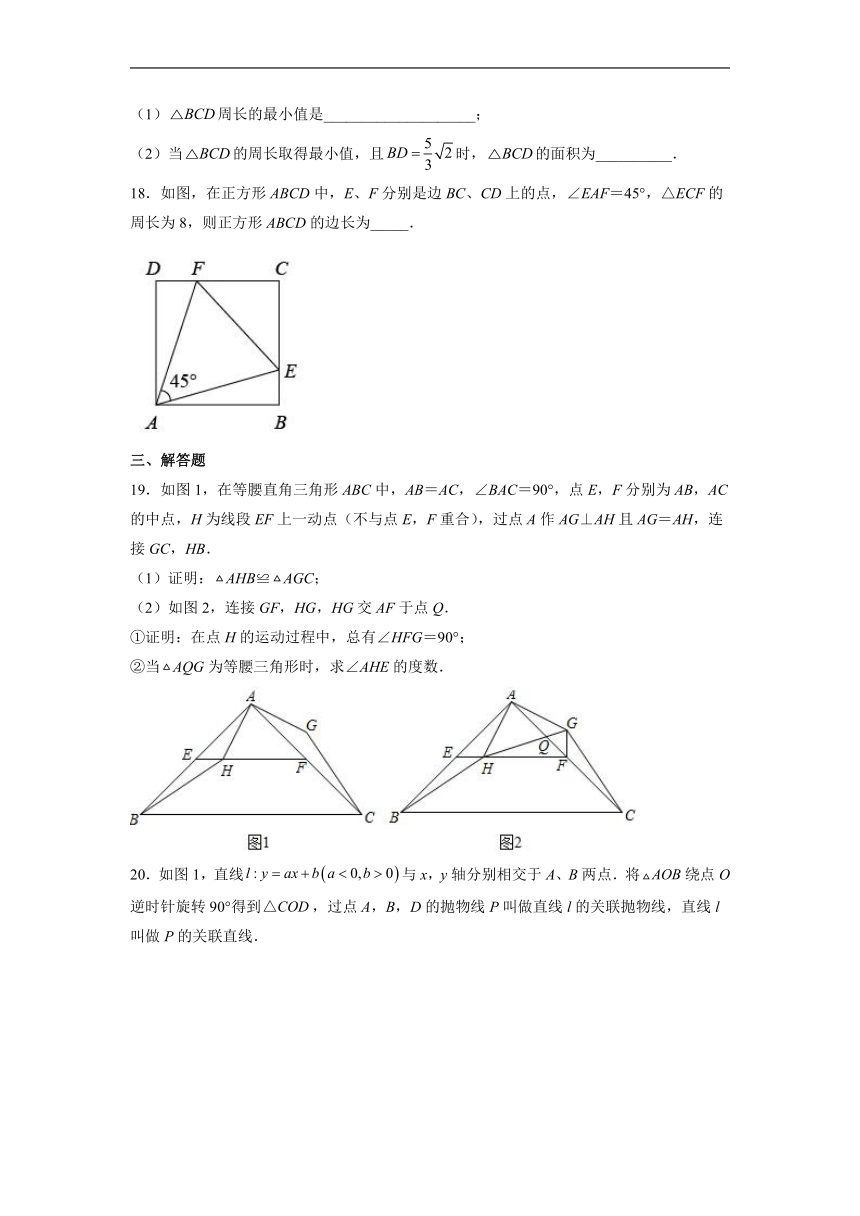
17.在平面直角坐标系中,直线分别交x轴、y轴于C、A两点.将射线绕着点A顺时针旋转,得到射线.点D为上的动点,点B为上的动点,点C在的内部.
(1)周长的最小值是____________________;
(2)当的周长取得最小值,且时,的面积为__________.
18.如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为8,则正方形ABCD的边长为_____.
三、解答题
19.如图1,在等腰直角三角形ABC中,AB=AC,∠BAC=90°,点E,F分别为AB,AC的中点,H为线段EF上一动点(不与点E,F重合),过点A作AG⊥AH且AG=AH,连接GC,HB.
(1)证明:AHB≌AGC;
(2)如图2,连接GF,HG,HG交AF于点Q.
①证明:在点H的运动过程中,总有∠HFG=90°;
②当AQG为等腰三角形时,求∠AHE的度数.
20.如图1,直线与x,y轴分别相交于A、B两点.将绕点O逆时针旋转90°得到,过点A,B,D的抛物线P叫做直线l的关联抛物线,直线l叫做P的关联直线.
(1)若直线,则抛物线P表示的函数解析式为______,若抛物线,则直线l表示的函数解析式为______;
(2)如图2,若直线,G为AB中点,H为CD的中点,连接GH,取GH中点M,连接OM,已知.求直线l的关联抛物线P表示的函数解析式;
(3)若将某直线的关联抛物线向右平移个单位得到抛物线,则a、m、n应满足的关系式为______.
21.问题发现:如图1,如果△ACB和△CDE均为等边三角形,点A、D、E在同一直线上,连接BE.
(1)如图1,请直接写出AD与BE的数量关系为________;
(2)如图1,求∠AEB的度数;
(3)拓展:如图2,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?
学生经过讨论,探究出以下解决问题的思路:
思路一:延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,等量代换得到AC=BC+CD.
思路二:将△ABC绕着点A逆时针旋转60°至△ADF,从而容易证明△ACF是等边三角形,故AC=CF,等量代换得到AC=BC+CD.
请选择一种思路,作出图形并写出证明过程.
22.在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC,点A、B的对应点分别是D、E.
(1)当点E恰好在AC上时,如图1,求∠ADE的大小;
(2)若α=60°时,点F是边AC中点,如图2,求证:四边形BEDF是平行四边形.
参考答案
1--10BABAC ACBCD 11--12BD
13.689
14.105°
15.或
16.
17.
18.4
19.(1)证明:如图1,
由旋转得:AH=AG,∠HAG=90°,
∵∠BAC=90°,
∴∠BAH=∠CAG,
∵AB=AC,
∴△ABH≌△ACG(SAS);
(2)①证明:如图2,在等腰直角三角形ABC中,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵点E,F分别为AB,AC的中点,
∴EF是△ABC的中位线,
∴EF∥BC,AE=AB,AF=AC,
∴AE=AF,∠AEF=∠ABC=45°,∠AFE=∠ACB=45°,
∵∠EAH=∠FAG,AH=AG,
∴△AEH≌△AFG(SAS),
∴∠AFG=∠AEH=45°,
∴∠HFG=45°+45°=90°;
②分两种情况:
i)如图3,AQ=QG时,
∵AQ=QG,
∴∠QAG=∠AGQ,
∵AG⊥AH且AG=AH,
∴∠AHG=∠AGH=45°,
∴∠AHG=∠AGH=∠HAQ=∠QAG=45°,
∴∠EAH=∠FAH=45°,
∵AE=AF,AH=AH,
∴△AEH≌△AFH(SAS),
∴∠AHE=∠AHF,
∵∠AHE+∠AHF=180°,
∴∠AHE=∠AHF=90°;
ii)如图4,当AG=QG时,∠GAQ=∠AQG,
∵∠AEH=∠AGQ=45°,
∴∠GAQ=∠AQG==67.5°,
∵∠EAQ=∠HAG=90°,
∴∠EAH=∠GAQ=67.5°,
∴∠AHE=∠AQG=67.5°;
∵H为线段EF上一动点(不与点E,F重合),
∴不存在AG=AQ的情况.
综上,当△AQG为等腰三角形时,∠AHE的度数为67.5°或90°.
20.(1)解:∵,当x=0时,y=2,当y=0时,x=1,∴A(1,0),B(0,2),根据旋转的全等性质,得到OD=0B=2,∴D(-2,0).设抛物线解析式为y=a(x-1)(x+2),把B的坐标代入解析式,得2=-2a,解得a=-1,∴;∵,∴,解得,∴A(1,0),D(-4,0),根据旋转性质,得到OB=OD=4,∴B(0,4).设直线的解析式为y=kx+4,把点A的坐标代入,得k+4=0,解得k=-4,∴y=-4x+4,故答案为:;.
(2)解:∵,∴A(4,0),B(0,-4t),根据旋转的全等性质,得到OD=OB=|-4t|= -4t,∴D(4t,0),∵G为AB中点,H为CD的中点,连接GH,取GH中点M,∴G(2,-2t),H(2t,2),M(t+1,1-t),根据勾股定理,得到,解得t=-2,t=2(舍去),故t=-2,∴A(4,0),B(0,8),D(-8,0),设抛物线解析式为y=a(x-4)(x+8),把B的坐标代入解析式,得8=-32a,解得a=,∴.
(3)解:∵某直线的关联抛物线向右平移个单位得到抛物线,∴将向左平移个单位得到关联抛物线,∴,∵>0,∴m<0,∴点A(m+n,0),D(2m,0),B(0,-2m),解得a(m+n)=-1,故答案为:a(m+n)=-1.
21.(1)解:∵和均为等边三角形,∴,,,∴∴,在和中,,∴,∴;故答案为:
(2)由(1)知,,∴,又,∴;
(3)如图:将绕着点逆时针旋转,至△ADF. ∵∠ACB=∠ACD=∠ABD=∠ADB=60°,∴∠DCB+∠BAD=180°,∴∠ABC+∠ADC=180°,∴∠ADF+∠ADC=180°,即:C,D,F三点共线,由旋转的性质得:,又∵,∴为等边三角形,∴,∴,∴
22.(1)解:∵△ABC绕点C顺时针旋转α得到△DEC,点E恰好在AC上,
∴CA=CD,∠ECD=∠BCA=30°,∠DEC=∠ABC=90°,
∴∠CAD=∠CDA=(180°﹣30°)=75°,
∴∠ADE=90°﹣∠CAD=15°;
(2)证明:如图2,连接AD
∵点F是边AC中点,
∴BF=AF=CF=AC,
∵∠ACB=30°,
∴AB=AC,
∴BF=CF=AB,
∵△ABC绕点C顺时针旋转60得到△DEC,
∴∠BCE=∠ACD=60°,CB=CE,DE=AB,DC=AC
∴DE=BF,△ACD和△BCE为等边三角形,
∴BE=CB,
∵点F为△ACD的边AC的中点,
∴DF⊥AC,
在Rt△CFD和Rt△ABC中
∴Rt△CFD≌Rt△ABC,
∴DF=BC,
∴DF=BE,
而BF=DE,
∴四边形BEDF是平行四边形.
一、单选题
1.下列现象中属于旋转的是( )
A.汽车在急刹车时向前滑动 B.拧开水龙头
C.雪橇在雪地里滑动 D.电梯的上升与下降
2.如图,在方格纸上建立的平面直角坐标系中,将绕点按顺时针方向旋转90°,得到,则点的坐标为( ).
A. B.
C. D.
3.如图,在方格纸中,将绕点按顺时针方向旋转90°后得到,则下列四个图形中正确的是( )
B.
C. D.
4.在平面直角坐标系中,点G的坐标是,连接,将线段绕原点O旋转,得到对应线段,则点的坐标为( )
A. B. C. D.
5.如图,将绕点逆时针旋转得到,若且于点,则的度数为( )
A. B. C. D.
6.如图,在中,, 将绕点逆时针旋转得到,其中点与 点是对应点,且点在同一条直线上;则的长为( )
A. B. C. D.
7.如图,将△ABC绕点B顺时针旋转50°得△DBE,点C的对应点恰好落在AB的延长线上,连接AD,下列结论不一定成立的是( )
A.AB=DB B.∠CBD=80° C.∠ABD=∠E D.△ABC≌△DBE
8.如图,已知菱形OABC的顶点O(0,0),B(2,2),菱形的对角线的交于点D;若将菱形OABC绕点O逆时针旋转,每秒旋转45°,从如图所示位置起,经过60秒时,菱形的对角线的交点D的坐标为( )
A.(1,1) B.(﹣1,﹣1) C.(-1,1) D.(1,﹣1)
9.将抛物线先绕坐标原点旋转,再向右平移个单位长度,所得抛物线的解析式为( )
A. B.
C. D.
10.如图,将绕点A按顺时针旋转一定角度得到,点B的对应点D恰好落在BC边上,若,,则CD的长为( ).
A. B. C. D.1
11.以原点为中心,将点P(4,5)按逆时针方向旋转90°,得到的点Q所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.如图,点A,B的坐标分别为(1,1)、(3,2),将△ABC绕点A按逆时针方向旋转90°,得到△A'B'C',则B'点的坐标为( )
A.(﹣1,3) B.(-1,2) C.(0,2) D.(0,3)
二、填空题
13.将数字“6”旋转,得到数字“9”,将数字“9”旋转,得到数字“6”,现将数字“689”整体旋转,得到的数字是______.
14.如图,将一个顶角为30°角的等腰△ABC绕点A顺时针旋转一个角度α(0<α<180°)得到△AB'C′,使得点B′、A、C在同一条直线上,则α等于_____°.
15.将正方形OEFG放在平面直角坐标系中,O是坐标原点,若点E的坐标为,则点G的坐标为_____.
16.如图,在中,,,,为内一点,则的最小值为__________.
17.在平面直角坐标系中,直线分别交x轴、y轴于C、A两点.将射线绕着点A顺时针旋转,得到射线.点D为上的动点,点B为上的动点,点C在的内部.
(1)周长的最小值是____________________;
(2)当的周长取得最小值,且时,的面积为__________.
18.如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为8,则正方形ABCD的边长为_____.
三、解答题
19.如图1,在等腰直角三角形ABC中,AB=AC,∠BAC=90°,点E,F分别为AB,AC的中点,H为线段EF上一动点(不与点E,F重合),过点A作AG⊥AH且AG=AH,连接GC,HB.
(1)证明:AHB≌AGC;
(2)如图2,连接GF,HG,HG交AF于点Q.
①证明:在点H的运动过程中,总有∠HFG=90°;
②当AQG为等腰三角形时,求∠AHE的度数.
20.如图1,直线与x,y轴分别相交于A、B两点.将绕点O逆时针旋转90°得到,过点A,B,D的抛物线P叫做直线l的关联抛物线,直线l叫做P的关联直线.
(1)若直线,则抛物线P表示的函数解析式为______,若抛物线,则直线l表示的函数解析式为______;
(2)如图2,若直线,G为AB中点,H为CD的中点,连接GH,取GH中点M,连接OM,已知.求直线l的关联抛物线P表示的函数解析式;
(3)若将某直线的关联抛物线向右平移个单位得到抛物线,则a、m、n应满足的关系式为______.
21.问题发现:如图1,如果△ACB和△CDE均为等边三角形,点A、D、E在同一直线上,连接BE.
(1)如图1,请直接写出AD与BE的数量关系为________;
(2)如图1,求∠AEB的度数;
(3)拓展:如图2,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?
学生经过讨论,探究出以下解决问题的思路:
思路一:延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,等量代换得到AC=BC+CD.
思路二:将△ABC绕着点A逆时针旋转60°至△ADF,从而容易证明△ACF是等边三角形,故AC=CF,等量代换得到AC=BC+CD.
请选择一种思路,作出图形并写出证明过程.
22.在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC,点A、B的对应点分别是D、E.
(1)当点E恰好在AC上时,如图1,求∠ADE的大小;
(2)若α=60°时,点F是边AC中点,如图2,求证:四边形BEDF是平行四边形.
参考答案
1--10BABAC ACBCD 11--12BD
13.689
14.105°
15.或
16.
17.
18.4
19.(1)证明:如图1,
由旋转得:AH=AG,∠HAG=90°,
∵∠BAC=90°,
∴∠BAH=∠CAG,
∵AB=AC,
∴△ABH≌△ACG(SAS);
(2)①证明:如图2,在等腰直角三角形ABC中,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵点E,F分别为AB,AC的中点,
∴EF是△ABC的中位线,
∴EF∥BC,AE=AB,AF=AC,
∴AE=AF,∠AEF=∠ABC=45°,∠AFE=∠ACB=45°,
∵∠EAH=∠FAG,AH=AG,
∴△AEH≌△AFG(SAS),
∴∠AFG=∠AEH=45°,
∴∠HFG=45°+45°=90°;
②分两种情况:
i)如图3,AQ=QG时,
∵AQ=QG,
∴∠QAG=∠AGQ,
∵AG⊥AH且AG=AH,
∴∠AHG=∠AGH=45°,
∴∠AHG=∠AGH=∠HAQ=∠QAG=45°,
∴∠EAH=∠FAH=45°,
∵AE=AF,AH=AH,
∴△AEH≌△AFH(SAS),
∴∠AHE=∠AHF,
∵∠AHE+∠AHF=180°,
∴∠AHE=∠AHF=90°;
ii)如图4,当AG=QG时,∠GAQ=∠AQG,
∵∠AEH=∠AGQ=45°,
∴∠GAQ=∠AQG==67.5°,
∵∠EAQ=∠HAG=90°,
∴∠EAH=∠GAQ=67.5°,
∴∠AHE=∠AQG=67.5°;
∵H为线段EF上一动点(不与点E,F重合),
∴不存在AG=AQ的情况.
综上,当△AQG为等腰三角形时,∠AHE的度数为67.5°或90°.
20.(1)解:∵,当x=0时,y=2,当y=0时,x=1,∴A(1,0),B(0,2),根据旋转的全等性质,得到OD=0B=2,∴D(-2,0).设抛物线解析式为y=a(x-1)(x+2),把B的坐标代入解析式,得2=-2a,解得a=-1,∴;∵,∴,解得,∴A(1,0),D(-4,0),根据旋转性质,得到OB=OD=4,∴B(0,4).设直线的解析式为y=kx+4,把点A的坐标代入,得k+4=0,解得k=-4,∴y=-4x+4,故答案为:;.
(2)解:∵,∴A(4,0),B(0,-4t),根据旋转的全等性质,得到OD=OB=|-4t|= -4t,∴D(4t,0),∵G为AB中点,H为CD的中点,连接GH,取GH中点M,∴G(2,-2t),H(2t,2),M(t+1,1-t),根据勾股定理,得到,解得t=-2,t=2(舍去),故t=-2,∴A(4,0),B(0,8),D(-8,0),设抛物线解析式为y=a(x-4)(x+8),把B的坐标代入解析式,得8=-32a,解得a=,∴.
(3)解:∵某直线的关联抛物线向右平移个单位得到抛物线,∴将向左平移个单位得到关联抛物线,∴,∵>0,∴m<0,∴点A(m+n,0),D(2m,0),B(0,-2m),解得a(m+n)=-1,故答案为:a(m+n)=-1.
21.(1)解:∵和均为等边三角形,∴,,,∴∴,在和中,,∴,∴;故答案为:
(2)由(1)知,,∴,又,∴;
(3)如图:将绕着点逆时针旋转,至△ADF. ∵∠ACB=∠ACD=∠ABD=∠ADB=60°,∴∠DCB+∠BAD=180°,∴∠ABC+∠ADC=180°,∴∠ADF+∠ADC=180°,即:C,D,F三点共线,由旋转的性质得:,又∵,∴为等边三角形,∴,∴,∴
22.(1)解:∵△ABC绕点C顺时针旋转α得到△DEC,点E恰好在AC上,
∴CA=CD,∠ECD=∠BCA=30°,∠DEC=∠ABC=90°,
∴∠CAD=∠CDA=(180°﹣30°)=75°,
∴∠ADE=90°﹣∠CAD=15°;
(2)证明:如图2,连接AD
∵点F是边AC中点,
∴BF=AF=CF=AC,
∵∠ACB=30°,
∴AB=AC,
∴BF=CF=AB,
∵△ABC绕点C顺时针旋转60得到△DEC,
∴∠BCE=∠ACD=60°,CB=CE,DE=AB,DC=AC
∴DE=BF,△ACD和△BCE为等边三角形,
∴BE=CB,
∵点F为△ACD的边AC的中点,
∴DF⊥AC,
在Rt△CFD和Rt△ABC中
∴Rt△CFD≌Rt△ABC,
∴DF=BC,
∴DF=BE,
而BF=DE,
∴四边形BEDF是平行四边形.
同课章节目录
