人教版九年级数学上册:第21章《一元二次方程》综合测试题(word、含解析)
文档属性
| 名称 | 人教版九年级数学上册:第21章《一元二次方程》综合测试题(word、含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 304.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 00:00:00 | ||
图片预览




文档简介
2022-2023学年人教版九年级数学上册
第21章《一元二次方程》综合测试题
一、单选题(共36分)
1.方程2x2﹣5x=4的二次项系数、一次项系数、常数项分别为( )
A.2,5,4 B.2,﹣5,4 C.﹣2,﹣5,4 D.2,﹣5,﹣4
2.已知x=﹣1是一元二次方程x2﹣x﹣m=0的解,则m的值为( )
A.1 B.﹣1 C.2 D.﹣2
3.一元二次方程3x2﹣2=4x可化成一般形式为( )
A.3x2﹣4x+2=0 B.3x2﹣4x﹣2=0 C.3x2+4x+2=0 D.3x2+4x﹣2=0
4.已知是方程的一个解,则的值为( )
A.10 B.-10 C.2 D.-40
5.已知m是一元二次方程的一个根,则代数式的值为( )
A.2018 B.2020 C.2022 D.2024
6.已知关于的一元二次方程的两根分别记为,,若,则的值为( )
A.7 B. C.6 D.
7.若分式的值为0,则( )
A.x=1或x=3 B.x=3 C.x=1 D.x≠1且x≠2
8.方程x2-(k2-4)x+k+1=0的两个实数根互为相反数,则k的值是( )
A.4或-4 B.2或-2 C.2 D.-2
9.有关于x的两个方程:ax2+bx+c=0与ax2-bx+c=0,其中abc>0,下列判断正确的是( )
A.两个方程可能一个有实数根,另一个没有实数根 B.若两个方程都有实数根,则必有一根互为相反数
C.若两个方程都有实数根,则必有一根相等 D.若两个方程都有实数根,则必有一根互为倒数
10.关于x的一元二次方程有两个不相等的实数根,则k的取值范围是( )
A. B.且 C. D.
11.有一个人患了流感,经过两轮后共有121个人患了流感,如果按照这样的传染速度,经过三轮传染后总共传染的人数是( )
A.1331 B.1000 C.1728 D.1111
12.某商店从厂家以每件18元的价格购进一批商品.该商品可以自行定价.据市场调查,该商品的售价与销售量的关系是:若每件售价a元,则可卖出件,但物价部门限定每件商品加价不能超过进货价的25%,如果商店计划要获利400元.则每件商品的售价应定为( )
A.22元 B.24元 C.26元 D.28元
二、填空题(共18分)
13.关于x的方程是一元二次方程,则________.
14.若a是方程的一个根,则代数式的值为________.
15.关于x的方程(m、n为实数且m≠0),m恰好是该方程的根,则m+n的值为_______.
16.已知是方程x2+2021x+1=0的两个根,则_____.
17.某商场将进价为30元的台灯以单价40元售出,平均每月能售出600个.调查表明:这种台灯的单价每上涨1元,其销售量将减少10个.为实现平均每月10000元的销售利润,从消费者的角度考虑,商场对这种台灯的售价应定为______元.
18.某地区加大教育投入,2021年投入教育经费2000万元,以后每年逐步增长,预计2023年,教育经费投入为2420万元,则该地区教育经费投入年平均增长率为______.
三、解答题(共66分)
19.(本题8分)解方程:
(1);
(2);
20.(本题9分)已知关于x的一元二次方程mx2﹣2x﹣1=0有两个不相等的实数根x1,x2.
(1)求m的取值范围;
(2)当时,求m的值.
21.(本题9分)已知关于x的一元二次方程.
(1)求证:方程总有两个实数根;
(2)若方程两个根的差是2,求实数的值.
22.(本题9分)如图,在长为50 m,宽为38 m的矩形地面内的四周修筑同样宽的道路,余下的铺上草坪.要使草坪的面积为1260 m2,道路的宽应为多少?
23.(本题10分)建设美丽城市,改造老旧小区.某市2019年投入资金1000万元,2021年投入资金1440万元,现假定每年投入资金的增长率相同.
(1)求该市改造老旧小区投入资金的年平均增长率;
(2)2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质,每个小区改造费用增加15%.如果投入资金年增长率保持不变,求该市在2022年最多可以改造多少个老旧小区?
24.(本题9分)我们知道:
;
,
这一种方法称为配方法,利用配方法请解以下各题:
(1)探究:当取不同的实数时,求代数式的最小值.
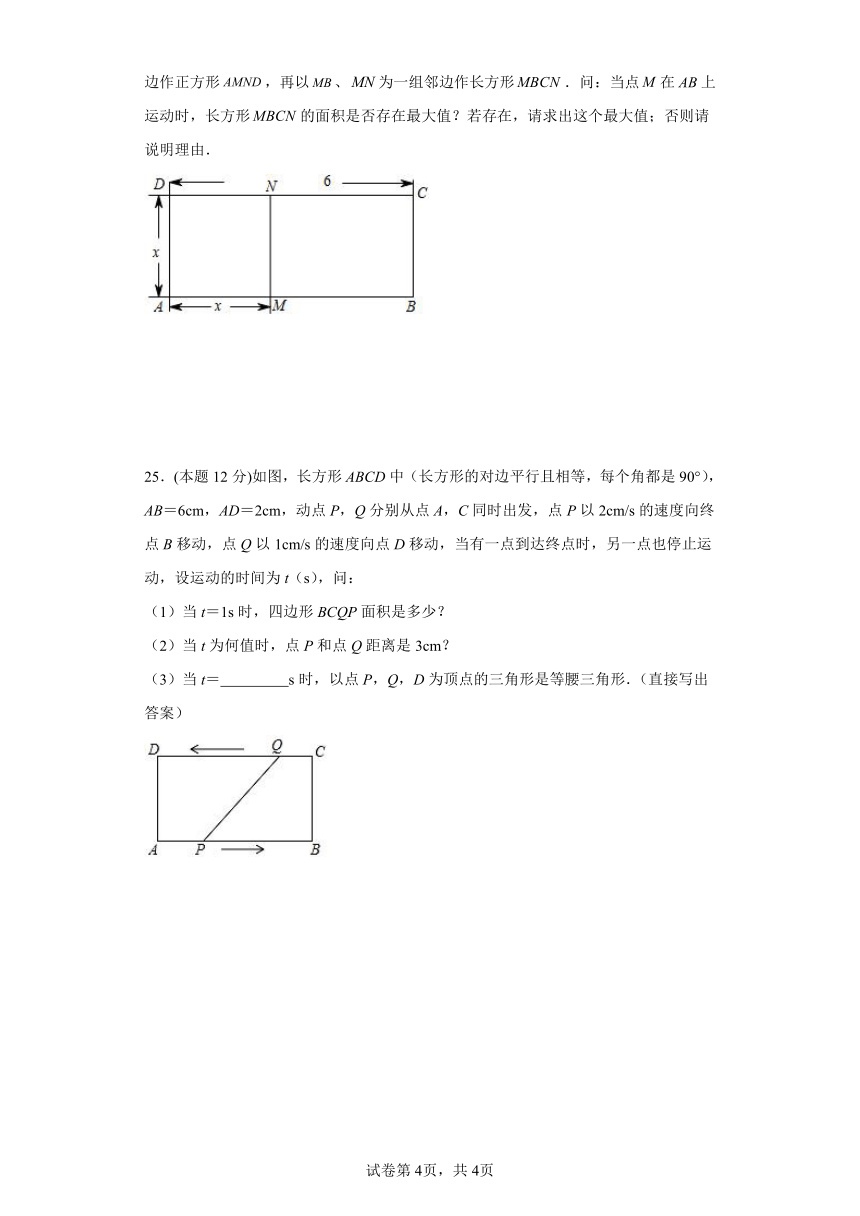
(2)应用:如图.已知线段,是上的一个动点,设,以为一边作正方形,再以、为一组邻边作长方形.问:当点在上运动时,长方形的面积是否存在最大值?若存在,请求出这个最大值;否则请说明理由.
25.(本题12分)如图,长方形ABCD中(长方形的对边平行且相等,每个角都是90°),AB=6cm,AD=2cm,动点P,Q分别从点A,C同时出发,点P以2cm/s的速度向终点B移动,点Q以1cm/s的速度向点D移动,当有一点到达终点时,另一点也停止运动,设运动的时间为t(s),问:
(1)当t=1s时,四边形BCQP面积是多少?
(2)当t为何值时,点P和点Q距离是3cm?
(3)当t= s时,以点P,Q,D为顶点的三角形是等腰三角形.(直接写出答案)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.D
解:∵方程2x2﹣5x=4化成一般形式是2x2﹣5x﹣4=0,
∴二次项系数为2,一次项系数为﹣5,常数项为﹣4.
故选:D.
2.C
把x=﹣1代入一元二次方程x2﹣x﹣m=0,再求解即可.
3.B
解:方程整理得:3x2﹣4x﹣2=0.
故选:B.
4.B
∵a是方程的一个解,
∴有,即,,
∴,
故选:B.
5.A
把x=m代入,可得,进而即可求解.
6.B
解:∵一元二次方程的两根分别记为,,
∴+=2,
∵,
∴=3,
∴·=-a=-3,
∴a=3,
∴.
7.B
解:∵分式的值为0,
∴
解得,
故选:B
8.D
解:∵方程x2-(k2-4)x+k+1=0的两实数根互为相反数,
∴k2-4=0,∴k=±2;
当k=2,方程变为:x2+1=0,Δ=-4<0,方程没有实数根,所以k=2舍去;
当k=-2,方程变为:x2-3=0,Δ=12>0,方程有两个不相等的实数根;
∴k=-2.
故选:D.
9.B
解:方程根的判别式为,
方程根的判别式为,
所以若一个方程有实数根,则另一个方程也一定有实数根,选项A错误;
若两个方程都有实数根,
设方程的一个实数根为,则,即,
,
,
,
将代入方程的左边得:,
即是方程的根,
所以此时两个方程必有一根互为相反数,选项B正确;
将代入方程的左边得:,
即不是方程的根,选项C错误;
将代入方程的左边得:
,
则只有当时,才是方程的根,
所以此时两个方程不一定有一根互为倒数,选项D错误;
故选:B.
10.B
根据题意可得再解不等式组,从而可得答案;
11.A
设平均一人传染了x人,根据有一人患了流感,经过两轮共有121人患了流感,列方程求解,进而表示出经过三轮传染后患上流感的人数.
12.A
根据利润和售价建立一元二次方程组,得到,解方程组得到售价,最后对售价的合理性进行判断即可得到最终的答案.
13.
解: 关于x的方程是一元二次方程,
由①得:
由②得:
所以
故答案为:
14.2019
解:∵a是方程一个根,
∴,
∴,
∴
,
故答案为:2019.
15.5
解:是该方程的根,
,
等式两边同时除以m得,,
.
故答案为:5.
16.1
解:∵α,β是方程x2+2021x+1=0的两个根,
∴α2+2021α+1=0,β2+2021β+1=0,αβ=1,
∴(α2+2022α+1)(β2+2022β+1)
=(α2+2021α+1+α)(β2+2021β+1+β)
=(0+α)(0+β)
=αβ
=1.
故答案是:1.
17.50
解:设商场对这种台灯的售价为x元,由题意得:
,
解得:,
由从消费者的角度考虑,可得这种台灯的售价应为50元;
故答案为50.
18.10%
解:设年平均增长率为x,由题意可得:2000(1+x)2=2420,
解得x=0.1=10%,或x=-2.1(不合题意舍去).
所以2021年到2023年该地区投入教育经费的年平均增长率为10%.
19.
(1)
解:(x+1)2=4x,
∴x2-2x+1=0,
∴(x-1)2=0,
∴x-1=0,
解得:x1=x2=1.
(2)
(x+4)2=5(x+4),
∴(x+4)2-5(x+4)=0,
∴(x+4)(x+4-5)=0,
∴x+4=0,x+4-5=0,
解得:x1=-4,x2=1.
20.
(1)解:关于x的一元二次方程有两个不相等的实数根, ,解得∶且;
(2)解:关于的一元二次方程mx -2x-1=0有两个不相等的实数根,,,,,即, 即, 解得∶,经检验,都是分式方程的解, m>-1且m≠0,.m的值为4.
21.
(1)证明:,∵ ≥0,∴方程总有两个实数根;
(2)解:,∴(x-1)(x-m-2)=0,∴x1=1,x2=m+2,∵方程两个根的差是2,∴若,则;若,则.∴实数的值为1或.
22.
解:设道路的宽应为x米,由题意得
(50-2x)×(38-2x)=1260
解得:x1=4,x2=40(不符合题意,舍去)
答:道路的宽应为4米.
23.
(1)解:设该市改造老旧小区投入资金的年平均增长率为,根据题意得:,解这个方程得,,,经检验,符合本题要求.答:该市改造老旧小区投入资金的年平均增长率为20%.
(2)设该市在2022年可以改造个老旧小区,由题意得:,解得.∵为正整数,∴最多可以改造18个小区.答:该市在2022年最多可以改造18个老旧小区.
24.
解:(1)∵,
∴当时,代数式存在最小值为-4;
(2)设长方形的面积为,
根据题意得:,
则时,存在最大值,最大值为9.
25
解:(1)如图,∵四边形ABCD是矩形,
∴AB=CD=6,AD=BC=2,∠A=∠B=∠C=∠D=90°.
∵CQ=1cm,AP=2cm,
∴AB=6﹣2=4(cm).
∴S=(cm2).
答:四边形BCQP面积是5cm2;
(2)如图1,作QE⊥AB于E,
∴∠PEQ=90°,
∵∠B=∠C=90°,
∴四边形BCQE是矩形,
∴QE=BC=2cm,BE=CQ=t(cm).
∵AP=2t(cm),
∴PE=6﹣2t﹣t=(6﹣3t)cm.
在Rt△PQE中,由勾股定理,得
(6﹣3t)2+4=9,
解得:t=.
如图2,作PE⊥CD于E,
∴∠PEQ=90°.
∵∠B=∠C=90°,
∴四边形BCQE是矩形,
∴PE=BC=2cm,BP=CE=6﹣2t.
∵CQ=t,
∴QE=t﹣(6﹣2t)=3t﹣6
在Rt△PEQ中,由勾股定理,得
(3t﹣6)2+4=9,
解得:t=.
综上所述:t=或;
(3)如图3,当PQ=DQ时,作QE⊥AB于E,
∴∠PEQ=90°,
∵∠B=∠C=90°,
∴四边形BCQE是矩形,
∴QE=BC=2cm,BE=CQ=t(cm).
∵AP=2t,
∴PE=6﹣2t﹣t=6﹣3t.DQ=6﹣t.
∵PQ=DQ,
∴PQ=6﹣t.
在Rt△PQE中,由勾股定理,得
(6﹣3t)2+4=(6﹣t)2,
解得:t=.
如图4,当PD=PQ时,作PE⊥DQ于E,
∴DE=QE=DQ,∠PED=90°.
∵∠A=∠D=90°,
∴四边形APED是矩形,
∴PE=AD=2cm.DE=AP=2t,
∵DQ=6﹣t,
∴DE= .
∴2t=,
解得:t=;
如图5,当PD=QD时,
∵AP=2t,CQ=t,
∴DQ=6﹣t,
∴PD=6﹣t.
在Rt△APD中,由勾股定理,得
4+4t2=(6﹣t)2,
解得t1=,t2=(舍去).
综上所述:t=或或或.
故答案为:或或或.
答案第1页,共2页
答案第1页,共2页
第21章《一元二次方程》综合测试题
一、单选题(共36分)
1.方程2x2﹣5x=4的二次项系数、一次项系数、常数项分别为( )
A.2,5,4 B.2,﹣5,4 C.﹣2,﹣5,4 D.2,﹣5,﹣4
2.已知x=﹣1是一元二次方程x2﹣x﹣m=0的解,则m的值为( )
A.1 B.﹣1 C.2 D.﹣2
3.一元二次方程3x2﹣2=4x可化成一般形式为( )
A.3x2﹣4x+2=0 B.3x2﹣4x﹣2=0 C.3x2+4x+2=0 D.3x2+4x﹣2=0
4.已知是方程的一个解,则的值为( )
A.10 B.-10 C.2 D.-40
5.已知m是一元二次方程的一个根,则代数式的值为( )
A.2018 B.2020 C.2022 D.2024
6.已知关于的一元二次方程的两根分别记为,,若,则的值为( )
A.7 B. C.6 D.
7.若分式的值为0,则( )
A.x=1或x=3 B.x=3 C.x=1 D.x≠1且x≠2
8.方程x2-(k2-4)x+k+1=0的两个实数根互为相反数,则k的值是( )
A.4或-4 B.2或-2 C.2 D.-2
9.有关于x的两个方程:ax2+bx+c=0与ax2-bx+c=0,其中abc>0,下列判断正确的是( )
A.两个方程可能一个有实数根,另一个没有实数根 B.若两个方程都有实数根,则必有一根互为相反数
C.若两个方程都有实数根,则必有一根相等 D.若两个方程都有实数根,则必有一根互为倒数
10.关于x的一元二次方程有两个不相等的实数根,则k的取值范围是( )
A. B.且 C. D.
11.有一个人患了流感,经过两轮后共有121个人患了流感,如果按照这样的传染速度,经过三轮传染后总共传染的人数是( )
A.1331 B.1000 C.1728 D.1111
12.某商店从厂家以每件18元的价格购进一批商品.该商品可以自行定价.据市场调查,该商品的售价与销售量的关系是:若每件售价a元,则可卖出件,但物价部门限定每件商品加价不能超过进货价的25%,如果商店计划要获利400元.则每件商品的售价应定为( )
A.22元 B.24元 C.26元 D.28元
二、填空题(共18分)
13.关于x的方程是一元二次方程,则________.
14.若a是方程的一个根,则代数式的值为________.
15.关于x的方程(m、n为实数且m≠0),m恰好是该方程的根,则m+n的值为_______.
16.已知是方程x2+2021x+1=0的两个根,则_____.
17.某商场将进价为30元的台灯以单价40元售出,平均每月能售出600个.调查表明:这种台灯的单价每上涨1元,其销售量将减少10个.为实现平均每月10000元的销售利润,从消费者的角度考虑,商场对这种台灯的售价应定为______元.
18.某地区加大教育投入,2021年投入教育经费2000万元,以后每年逐步增长,预计2023年,教育经费投入为2420万元,则该地区教育经费投入年平均增长率为______.
三、解答题(共66分)
19.(本题8分)解方程:
(1);
(2);
20.(本题9分)已知关于x的一元二次方程mx2﹣2x﹣1=0有两个不相等的实数根x1,x2.
(1)求m的取值范围;
(2)当时,求m的值.
21.(本题9分)已知关于x的一元二次方程.
(1)求证:方程总有两个实数根;
(2)若方程两个根的差是2,求实数的值.
22.(本题9分)如图,在长为50 m,宽为38 m的矩形地面内的四周修筑同样宽的道路,余下的铺上草坪.要使草坪的面积为1260 m2,道路的宽应为多少?
23.(本题10分)建设美丽城市,改造老旧小区.某市2019年投入资金1000万元,2021年投入资金1440万元,现假定每年投入资金的增长率相同.
(1)求该市改造老旧小区投入资金的年平均增长率;
(2)2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质,每个小区改造费用增加15%.如果投入资金年增长率保持不变,求该市在2022年最多可以改造多少个老旧小区?
24.(本题9分)我们知道:
;
,
这一种方法称为配方法,利用配方法请解以下各题:
(1)探究:当取不同的实数时,求代数式的最小值.
(2)应用:如图.已知线段,是上的一个动点,设,以为一边作正方形,再以、为一组邻边作长方形.问:当点在上运动时,长方形的面积是否存在最大值?若存在,请求出这个最大值;否则请说明理由.
25.(本题12分)如图,长方形ABCD中(长方形的对边平行且相等,每个角都是90°),AB=6cm,AD=2cm,动点P,Q分别从点A,C同时出发,点P以2cm/s的速度向终点B移动,点Q以1cm/s的速度向点D移动,当有一点到达终点时,另一点也停止运动,设运动的时间为t(s),问:
(1)当t=1s时,四边形BCQP面积是多少?
(2)当t为何值时,点P和点Q距离是3cm?
(3)当t= s时,以点P,Q,D为顶点的三角形是等腰三角形.(直接写出答案)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.D
解:∵方程2x2﹣5x=4化成一般形式是2x2﹣5x﹣4=0,
∴二次项系数为2,一次项系数为﹣5,常数项为﹣4.
故选:D.
2.C
把x=﹣1代入一元二次方程x2﹣x﹣m=0,再求解即可.
3.B
解:方程整理得:3x2﹣4x﹣2=0.
故选:B.
4.B
∵a是方程的一个解,
∴有,即,,
∴,
故选:B.
5.A
把x=m代入,可得,进而即可求解.
6.B
解:∵一元二次方程的两根分别记为,,
∴+=2,
∵,
∴=3,
∴·=-a=-3,
∴a=3,
∴.
7.B
解:∵分式的值为0,
∴
解得,
故选:B
8.D
解:∵方程x2-(k2-4)x+k+1=0的两实数根互为相反数,
∴k2-4=0,∴k=±2;
当k=2,方程变为:x2+1=0,Δ=-4<0,方程没有实数根,所以k=2舍去;
当k=-2,方程变为:x2-3=0,Δ=12>0,方程有两个不相等的实数根;
∴k=-2.
故选:D.
9.B
解:方程根的判别式为,
方程根的判别式为,
所以若一个方程有实数根,则另一个方程也一定有实数根,选项A错误;
若两个方程都有实数根,
设方程的一个实数根为,则,即,
,
,
,
将代入方程的左边得:,
即是方程的根,
所以此时两个方程必有一根互为相反数,选项B正确;
将代入方程的左边得:,
即不是方程的根,选项C错误;
将代入方程的左边得:
,
则只有当时,才是方程的根,
所以此时两个方程不一定有一根互为倒数,选项D错误;
故选:B.
10.B
根据题意可得再解不等式组,从而可得答案;
11.A
设平均一人传染了x人,根据有一人患了流感,经过两轮共有121人患了流感,列方程求解,进而表示出经过三轮传染后患上流感的人数.
12.A
根据利润和售价建立一元二次方程组,得到,解方程组得到售价,最后对售价的合理性进行判断即可得到最终的答案.
13.
解: 关于x的方程是一元二次方程,
由①得:
由②得:
所以
故答案为:
14.2019
解:∵a是方程一个根,
∴,
∴,
∴
,
故答案为:2019.
15.5
解:是该方程的根,
,
等式两边同时除以m得,,
.
故答案为:5.
16.1
解:∵α,β是方程x2+2021x+1=0的两个根,
∴α2+2021α+1=0,β2+2021β+1=0,αβ=1,
∴(α2+2022α+1)(β2+2022β+1)
=(α2+2021α+1+α)(β2+2021β+1+β)
=(0+α)(0+β)
=αβ
=1.
故答案是:1.
17.50
解:设商场对这种台灯的售价为x元,由题意得:
,
解得:,
由从消费者的角度考虑,可得这种台灯的售价应为50元;
故答案为50.
18.10%
解:设年平均增长率为x,由题意可得:2000(1+x)2=2420,
解得x=0.1=10%,或x=-2.1(不合题意舍去).
所以2021年到2023年该地区投入教育经费的年平均增长率为10%.
19.
(1)
解:(x+1)2=4x,
∴x2-2x+1=0,
∴(x-1)2=0,
∴x-1=0,
解得:x1=x2=1.
(2)
(x+4)2=5(x+4),
∴(x+4)2-5(x+4)=0,
∴(x+4)(x+4-5)=0,
∴x+4=0,x+4-5=0,
解得:x1=-4,x2=1.
20.
(1)解:关于x的一元二次方程有两个不相等的实数根, ,解得∶且;
(2)解:关于的一元二次方程mx -2x-1=0有两个不相等的实数根,,,,,即, 即, 解得∶,经检验,都是分式方程的解, m>-1且m≠0,.m的值为4.
21.
(1)证明:,∵ ≥0,∴方程总有两个实数根;
(2)解:,∴(x-1)(x-m-2)=0,∴x1=1,x2=m+2,∵方程两个根的差是2,∴若,则;若,则.∴实数的值为1或.
22.
解:设道路的宽应为x米,由题意得
(50-2x)×(38-2x)=1260
解得:x1=4,x2=40(不符合题意,舍去)
答:道路的宽应为4米.
23.
(1)解:设该市改造老旧小区投入资金的年平均增长率为,根据题意得:,解这个方程得,,,经检验,符合本题要求.答:该市改造老旧小区投入资金的年平均增长率为20%.
(2)设该市在2022年可以改造个老旧小区,由题意得:,解得.∵为正整数,∴最多可以改造18个小区.答:该市在2022年最多可以改造18个老旧小区.
24.
解:(1)∵,
∴当时,代数式存在最小值为-4;
(2)设长方形的面积为,
根据题意得:,
则时,存在最大值,最大值为9.
25
解:(1)如图,∵四边形ABCD是矩形,
∴AB=CD=6,AD=BC=2,∠A=∠B=∠C=∠D=90°.
∵CQ=1cm,AP=2cm,
∴AB=6﹣2=4(cm).
∴S=(cm2).
答:四边形BCQP面积是5cm2;
(2)如图1,作QE⊥AB于E,
∴∠PEQ=90°,
∵∠B=∠C=90°,
∴四边形BCQE是矩形,
∴QE=BC=2cm,BE=CQ=t(cm).
∵AP=2t(cm),
∴PE=6﹣2t﹣t=(6﹣3t)cm.
在Rt△PQE中,由勾股定理,得
(6﹣3t)2+4=9,
解得:t=.
如图2,作PE⊥CD于E,
∴∠PEQ=90°.
∵∠B=∠C=90°,
∴四边形BCQE是矩形,
∴PE=BC=2cm,BP=CE=6﹣2t.
∵CQ=t,
∴QE=t﹣(6﹣2t)=3t﹣6
在Rt△PEQ中,由勾股定理,得
(3t﹣6)2+4=9,
解得:t=.
综上所述:t=或;
(3)如图3,当PQ=DQ时,作QE⊥AB于E,
∴∠PEQ=90°,
∵∠B=∠C=90°,
∴四边形BCQE是矩形,
∴QE=BC=2cm,BE=CQ=t(cm).
∵AP=2t,
∴PE=6﹣2t﹣t=6﹣3t.DQ=6﹣t.
∵PQ=DQ,
∴PQ=6﹣t.
在Rt△PQE中,由勾股定理,得
(6﹣3t)2+4=(6﹣t)2,
解得:t=.
如图4,当PD=PQ时,作PE⊥DQ于E,
∴DE=QE=DQ,∠PED=90°.
∵∠A=∠D=90°,
∴四边形APED是矩形,
∴PE=AD=2cm.DE=AP=2t,
∵DQ=6﹣t,
∴DE= .
∴2t=,
解得:t=;
如图5,当PD=QD时,
∵AP=2t,CQ=t,
∴DQ=6﹣t,
∴PD=6﹣t.
在Rt△APD中,由勾股定理,得
4+4t2=(6﹣t)2,
解得t1=,t2=(舍去).
综上所述:t=或或或.
故答案为:或或或.
答案第1页,共2页
答案第1页,共2页
同课章节目录
