人教版选修二 1.4 质谱仪与回旋加速器 课件(26张PPT)
文档属性
| 名称 | 人教版选修二 1.4 质谱仪与回旋加速器 课件(26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 22.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-08-07 22:44:37 | ||
图片预览






文档简介
(共26张PPT)
横县百合完全中学:韦衍虎
18276143537
1.4质谱仪与回旋加速器
问题导入
在科学研究和工业生产中,常需要将一束带等量电荷的粒子分开,以便知道其中所含物质的成分。利用所学的知识,你能设计一个方案,以便分开电荷量相同、质量不同的带电粒子吗
质谱仪是用来分离同位素、检测它们的相对原子质量和相对丰度的仪器。
我们知道,电场可以对带电粒子施加作用力,磁场也可以对运动的带电粒子施加作用力。
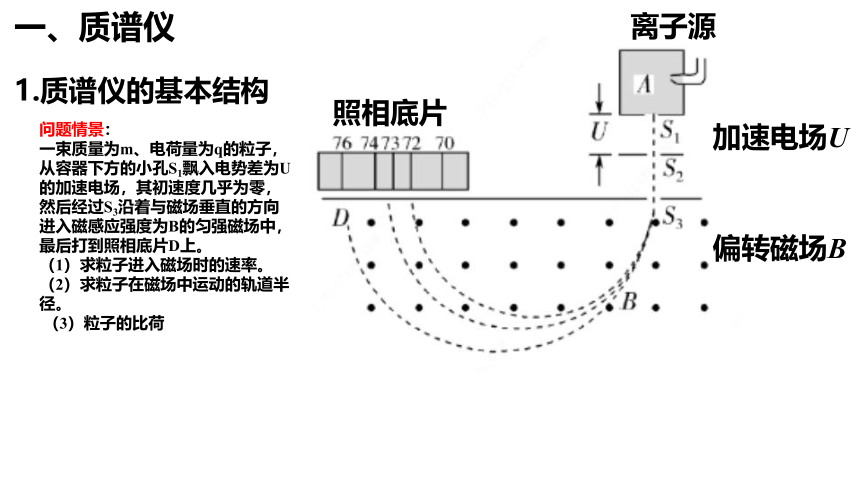
一、质谱仪
1.质谱仪的基本结构
离子源
加速电场U
偏转磁场B
照相底片
问题情景:
一束质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,其初速度几乎为零,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上。
(1)求粒子进入磁场时的速率。
(2)求粒子在磁场中运动的轨道半径。
(3)粒子的比荷
2.质谱仪的工作原理
①在电场中加速
②在偏转磁场中,洛伦兹力提供向心力
联立两个式子得:
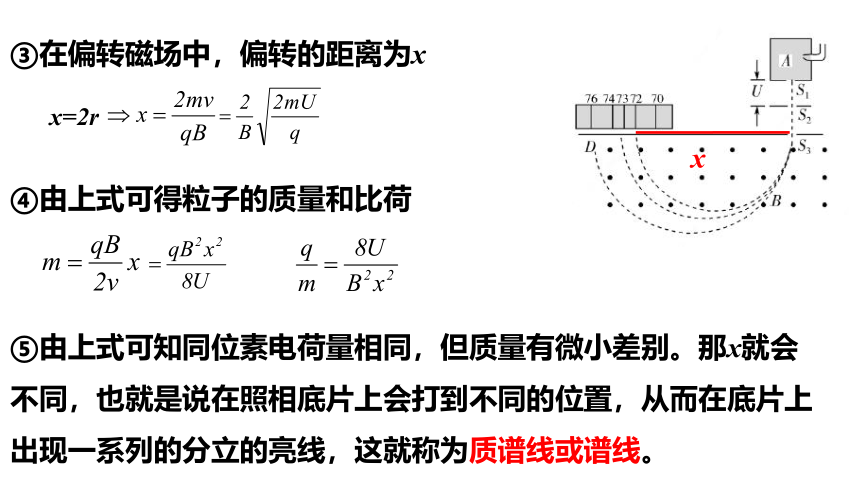
③在偏转磁场中,偏转的距离为x
x
x=2r
④由上式可得粒子的质量和比荷
⑤由上式可知同位素电荷量相同,但质量有微小差别。那x就会不同,也就是说在照相底片上会打到不同的位置,从而在底片上出现一系列的分立的亮线,这就称为质谱线或谱线。
例1:同一种带电粒子以不同的速度垂直磁场便捷、垂直磁感线射入匀强磁场中,其运动轨迹如图所示,则可知:
(1)带电粒子进入磁场的速度值有几个?
(2)这些速度的大小关系为?
(3)三束粒子从O点出发分别到达1、2、3
点所用时间的大小关系是?
课堂练习
3
v1t1=t2=t3
二、回旋加速器
要认识原子核内部的情况,必须把核“打开”进行“观察”。然而,原子核被强大的核力约束,只有用极高能量的粒子作为“炮弹”去轰击,才能把它“打开”。产生高能“炮弹”的“工厂”就是各种各样的粒子加速器。
问题1:用什么方法可以加速带电粒子
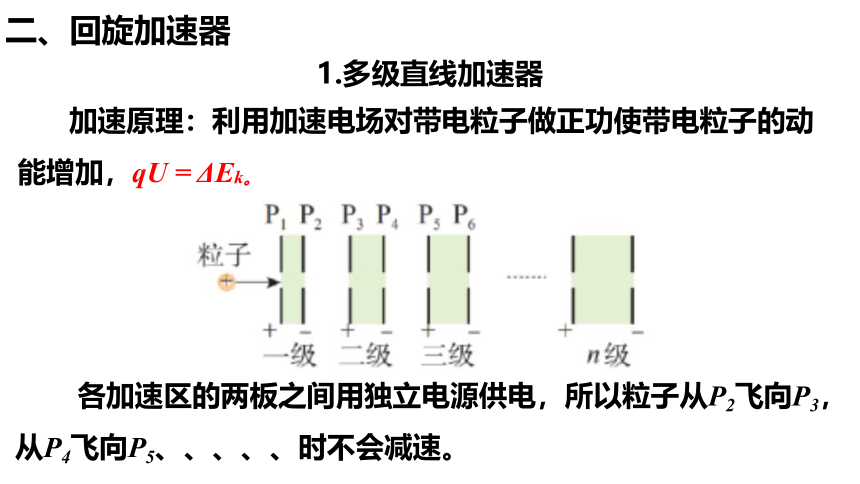
二、回旋加速器
1.多级直线加速器
加速原理:利用加速电场对带电粒子做正功使带电粒子的动能增加,qU = ΔEk。
各加速区的两板之间用独立电源供电,所以粒子从P2飞向P3,从P4飞向P5、、、、、时不会减速。
直线加速器占有的空间范围大,在有限的空间范围内制造直线加速器受到一定的限制。
1966年建成得的斯坦福大学的加速器管长3050米
北京正负电子对撞机改造后的直线加速器为建设科技强国加速
人们进一步思考:如果带电粒子在一次加速后又转回来被第二次加速,如此往复“转圈圈”式地被加速,加速器装置所占的空间不是会大大缩小吗?而磁场正好能使带电粒“转圈圈”!于是,人们依据这个思路设计出了用磁场控制轨道、用电场进行加速的回旋加速器。
1932年,美国物理学家劳仑斯发明了回旋加速器,
从而使人类在获得具有较高能量的粒子方面迈进了一大步.为此,劳仑斯荣获了诺贝尔物理学奖.
2.回旋加速器
①基本结构
粒子源
接交流电源
金属盒内部的电场为零
②工作原理
正电
A0
v0
A/2
v1
A1
A/1
A2
v2
粒子就会不断的加速
a、粒子源发出粒子
b、在磁场中做半个周期的匀速圆周运动
c、在电场中加速
思考与讨论:怎么控制电场的变化呢?
周期 ,与速度无关,故周期始终不变。
同频变化
粒子将会从粒子引出口飞出D形盒,结束加速的过程
当粒子做圆周运动的半径与D形盒半径R相同时
r=R
最大速度
最大动能
U
每次Δv
Δr
次数少
t短
U
每次Δv
Δr
次数多
t长
在磁场中做圆周运动,周期不变
电场的周期与粒子在磁场中做圆周运动周期相同-----保证粒子每次经过交变电场时都被加速
电场一个周期中方向变化两次,每一个周期加速两次
4.粒子加速的最大速度由盒的半径决定
5.电场加速过程中,时间极短,可忽略
结论
北京正负电子对撞机是世界八大高能加速器中心之一.1988年10月16日,两束正负电子在北京西郊一个羽毛球拍状的巨型机器里成功对撞,揭开了我国高能物理研究的新篇章。
目前世界上最大的回旋加速器在美国费米加速实验室,环形管道的半径为2公里。产生的高能粒子能量为5000亿电子伏特。
这个过程看似可以一直进行下去,但实际上由于相对论的效应,粒子的质量会随着速度增,圆周运动的周期也增加,这样电场于运动不在同步,也就没办法加速了。
例2:回加速器D形盒的半径为r,匀强磁场的磁感应强度为B。一个质量为m、电荷量为q的粒子在加速器的中央从速度为0开始加速。根据回旋加速器的这些数据估算该粒子离开回旋加速器时获得的动能。
课堂练习
解:当带电粒子离开回旋加速器时其速度达到最大,其运动半径也最大,由
所以加速次数:
所以加速总时间:
例2:回加速器D形盒的半径为r,匀强磁场的磁感应强度为B。一个质量为m、电荷量为q的粒子在加速器的中央从速度为0开始加速。根据回旋加速器的这些数据估算该粒子离开回旋加速器时获得的动能。
如已知加速电压为U,忽略在电场中运动时间,求加速的次数和加速的总时间。
解:每次加速得到的动能
EK=qU
由于圆周运动的周期:
例 (多选)一个用于加速质子的回旋加速器,其核心部分如图所示,D形盒半径为R,垂直D形盒底面的匀强磁场的磁感应强度为B,两盒分别与交流电源相连。设质子的质量为m、电荷量为q,则下列说法正确的是( )
B.质子被加速后的最大速度随B、R的增大而增大
C.质子被加速后的最大速度随加速电压的增大而增大
D.只要R足够大,质子的速度可以被加速到任意值
A B
回旋加速器加速的带电粒子的最终能量由哪些因素决定
观点1:认为电场是用来加速的,磁场是用来回旋的,最终的能量应与磁场无关。应与电场有关,加速电压越高,粒子最终能量越高。对吗?
观点2:
运动半径最大Rm=mVm/qB,得 Vm=qBRm/m
半径最大时,速度也应最大。
带电粒子的运动最大半径等于D形盒的半径时,粒子的速度达到最大。对吗?
U,B.R还是其它
课堂小结
1.质谱仪
①在电场中加速
②在偏转磁场中,洛伦兹力提供向心力
③在偏转磁场中,偏转的距离为
x=2r
④由上式可得粒子的质量和比荷
2.多级直线加速器
①加速原理:在电场中加速,qU = ΔEk。
②缺点:占有的空间范围大
①当粒子做圆周运动的半径与D形盒半径R相同时:
r=R
最大速度
最大动能
加速次数
加速总时间
②缺点:受相对论影响,无法一直加速
3.回旋加速器
横县百合完全中学:韦衍虎
18276143537
1.4质谱仪与回旋加速器
问题导入
在科学研究和工业生产中,常需要将一束带等量电荷的粒子分开,以便知道其中所含物质的成分。利用所学的知识,你能设计一个方案,以便分开电荷量相同、质量不同的带电粒子吗
质谱仪是用来分离同位素、检测它们的相对原子质量和相对丰度的仪器。
我们知道,电场可以对带电粒子施加作用力,磁场也可以对运动的带电粒子施加作用力。
一、质谱仪
1.质谱仪的基本结构
离子源
加速电场U
偏转磁场B
照相底片
问题情景:
一束质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,其初速度几乎为零,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上。
(1)求粒子进入磁场时的速率。
(2)求粒子在磁场中运动的轨道半径。
(3)粒子的比荷
2.质谱仪的工作原理
①在电场中加速
②在偏转磁场中,洛伦兹力提供向心力
联立两个式子得:
③在偏转磁场中,偏转的距离为x
x
x=2r
④由上式可得粒子的质量和比荷
⑤由上式可知同位素电荷量相同,但质量有微小差别。那x就会不同,也就是说在照相底片上会打到不同的位置,从而在底片上出现一系列的分立的亮线,这就称为质谱线或谱线。
例1:同一种带电粒子以不同的速度垂直磁场便捷、垂直磁感线射入匀强磁场中,其运动轨迹如图所示,则可知:
(1)带电粒子进入磁场的速度值有几个?
(2)这些速度的大小关系为?
(3)三束粒子从O点出发分别到达1、2、3
点所用时间的大小关系是?
课堂练习
3
v1
二、回旋加速器
要认识原子核内部的情况,必须把核“打开”进行“观察”。然而,原子核被强大的核力约束,只有用极高能量的粒子作为“炮弹”去轰击,才能把它“打开”。产生高能“炮弹”的“工厂”就是各种各样的粒子加速器。
问题1:用什么方法可以加速带电粒子
二、回旋加速器
1.多级直线加速器
加速原理:利用加速电场对带电粒子做正功使带电粒子的动能增加,qU = ΔEk。
各加速区的两板之间用独立电源供电,所以粒子从P2飞向P3,从P4飞向P5、、、、、时不会减速。
直线加速器占有的空间范围大,在有限的空间范围内制造直线加速器受到一定的限制。
1966年建成得的斯坦福大学的加速器管长3050米
北京正负电子对撞机改造后的直线加速器为建设科技强国加速
人们进一步思考:如果带电粒子在一次加速后又转回来被第二次加速,如此往复“转圈圈”式地被加速,加速器装置所占的空间不是会大大缩小吗?而磁场正好能使带电粒“转圈圈”!于是,人们依据这个思路设计出了用磁场控制轨道、用电场进行加速的回旋加速器。
1932年,美国物理学家劳仑斯发明了回旋加速器,
从而使人类在获得具有较高能量的粒子方面迈进了一大步.为此,劳仑斯荣获了诺贝尔物理学奖.
2.回旋加速器
①基本结构
粒子源
接交流电源
金属盒内部的电场为零
②工作原理
正电
A0
v0
A/2
v1
A1
A/1
A2
v2
粒子就会不断的加速
a、粒子源发出粒子
b、在磁场中做半个周期的匀速圆周运动
c、在电场中加速
思考与讨论:怎么控制电场的变化呢?
周期 ,与速度无关,故周期始终不变。
同频变化
粒子将会从粒子引出口飞出D形盒,结束加速的过程
当粒子做圆周运动的半径与D形盒半径R相同时
r=R
最大速度
最大动能
U
每次Δv
Δr
次数少
t短
U
每次Δv
Δr
次数多
t长
在磁场中做圆周运动,周期不变
电场的周期与粒子在磁场中做圆周运动周期相同-----保证粒子每次经过交变电场时都被加速
电场一个周期中方向变化两次,每一个周期加速两次
4.粒子加速的最大速度由盒的半径决定
5.电场加速过程中,时间极短,可忽略
结论
北京正负电子对撞机是世界八大高能加速器中心之一.1988年10月16日,两束正负电子在北京西郊一个羽毛球拍状的巨型机器里成功对撞,揭开了我国高能物理研究的新篇章。
目前世界上最大的回旋加速器在美国费米加速实验室,环形管道的半径为2公里。产生的高能粒子能量为5000亿电子伏特。
这个过程看似可以一直进行下去,但实际上由于相对论的效应,粒子的质量会随着速度增,圆周运动的周期也增加,这样电场于运动不在同步,也就没办法加速了。
例2:回加速器D形盒的半径为r,匀强磁场的磁感应强度为B。一个质量为m、电荷量为q的粒子在加速器的中央从速度为0开始加速。根据回旋加速器的这些数据估算该粒子离开回旋加速器时获得的动能。
课堂练习
解:当带电粒子离开回旋加速器时其速度达到最大,其运动半径也最大,由
所以加速次数:
所以加速总时间:
例2:回加速器D形盒的半径为r,匀强磁场的磁感应强度为B。一个质量为m、电荷量为q的粒子在加速器的中央从速度为0开始加速。根据回旋加速器的这些数据估算该粒子离开回旋加速器时获得的动能。
如已知加速电压为U,忽略在电场中运动时间,求加速的次数和加速的总时间。
解:每次加速得到的动能
EK=qU
由于圆周运动的周期:
例 (多选)一个用于加速质子的回旋加速器,其核心部分如图所示,D形盒半径为R,垂直D形盒底面的匀强磁场的磁感应强度为B,两盒分别与交流电源相连。设质子的质量为m、电荷量为q,则下列说法正确的是( )
B.质子被加速后的最大速度随B、R的增大而增大
C.质子被加速后的最大速度随加速电压的增大而增大
D.只要R足够大,质子的速度可以被加速到任意值
A B
回旋加速器加速的带电粒子的最终能量由哪些因素决定
观点1:认为电场是用来加速的,磁场是用来回旋的,最终的能量应与磁场无关。应与电场有关,加速电压越高,粒子最终能量越高。对吗?
观点2:
运动半径最大Rm=mVm/qB,得 Vm=qBRm/m
半径最大时,速度也应最大。
带电粒子的运动最大半径等于D形盒的半径时,粒子的速度达到最大。对吗?
U,B.R还是其它
课堂小结
1.质谱仪
①在电场中加速
②在偏转磁场中,洛伦兹力提供向心力
③在偏转磁场中,偏转的距离为
x=2r
④由上式可得粒子的质量和比荷
2.多级直线加速器
①加速原理:在电场中加速,qU = ΔEk。
②缺点:占有的空间范围大
①当粒子做圆周运动的半径与D形盒半径R相同时:
r=R
最大速度
最大动能
加速次数
加速总时间
②缺点:受相对论影响,无法一直加速
3.回旋加速器
