11.2.1 三角形的内角(2) 课件(共24张PPT)
文档属性
| 名称 | 11.2.1 三角形的内角(2) 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 957.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
人教版 八年级上册
11.2.1 三角形的内角(2)
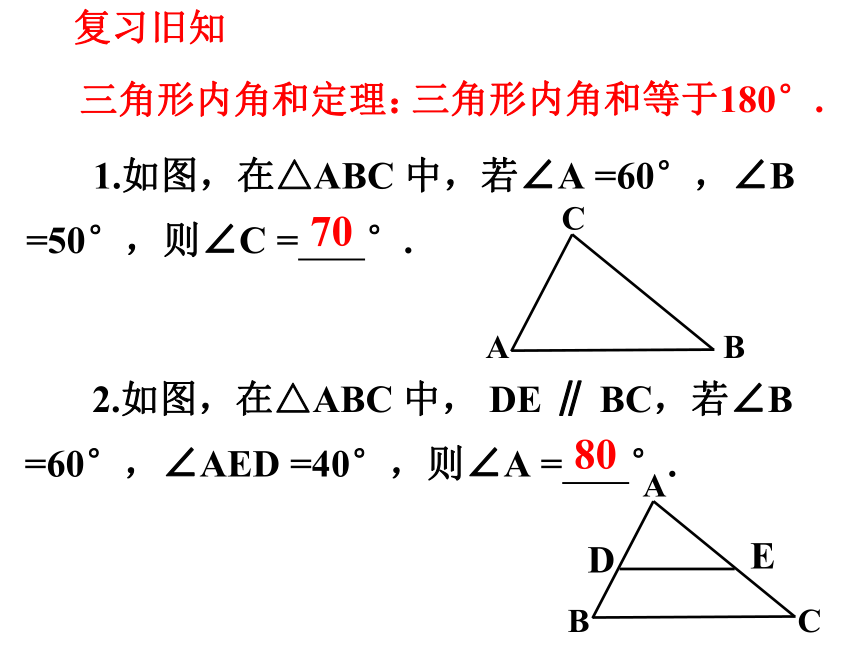
复习旧知
三角形内角和定理:
三角形内角和等于180°.
1.如图,在△ABC 中,若∠A =60°,∠B =50°,则∠C = °.
2.如图,在△ABC 中, DE ∥ BC,若∠B =60°,∠AED =40°,则∠A = °.
A
B
C
B
C
A
D
E
70
80
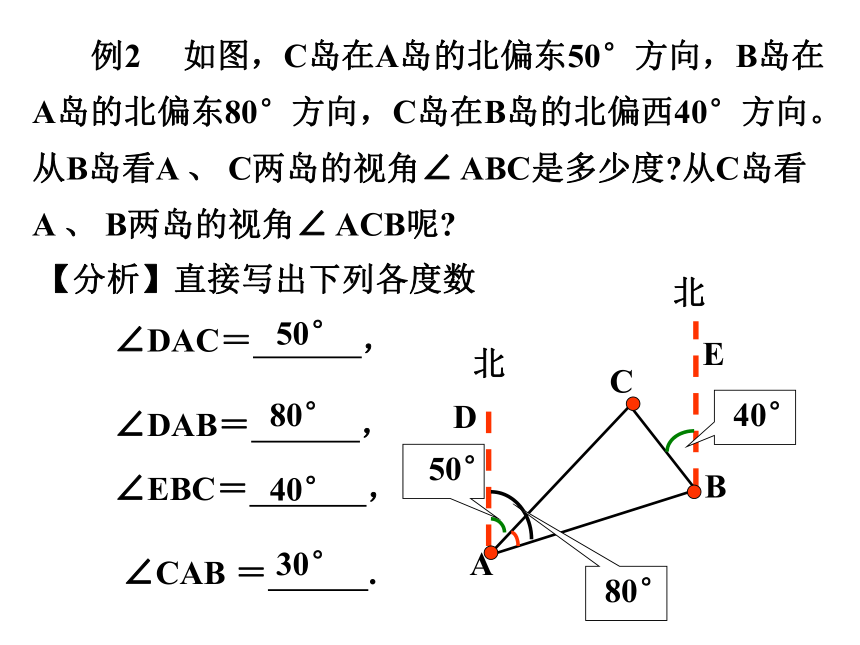
例2 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从B岛看A 、 C两岛的视角∠ ABC是多少度 从C岛看A 、 B两岛的视角∠ ACB呢
A
D
B
C
E
北
北
【分析】直接写出下列各度数
∠DAC= ,
∠DAB= , ∠EBC= ,
∠CAB = .
50°
80°
40°
50°
80°
40°
30°
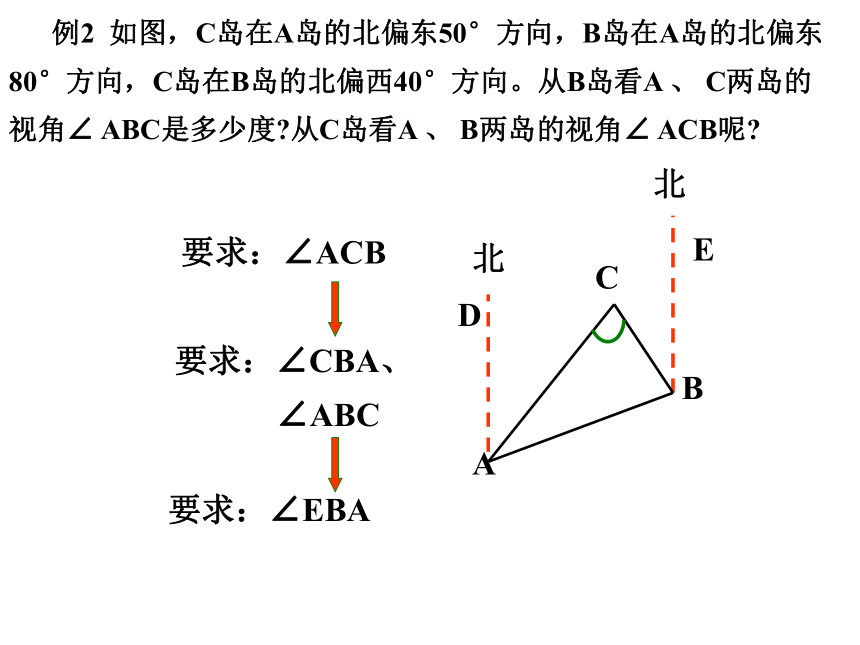
例2 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从B岛看A 、 C两岛的视角∠ ABC是多少度 从C岛看A 、 B两岛的视角∠ ACB呢
A
D
B
C
E
北
北
要求:∠EBA
要求:∠CBA、
要求:∠ACB
∠ABC
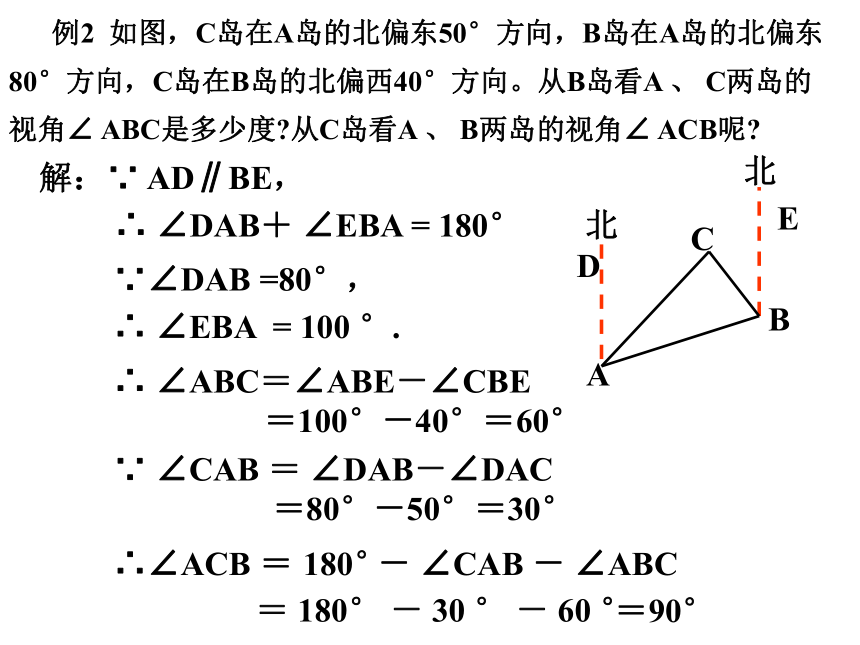
例2 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从B岛看A 、 C两岛的视角∠ ABC是多少度 从C岛看A 、 B两岛的视角∠ ACB呢
A
D
B
C
E
北
北
解:∵ AD∥BE,
∴ ∠DAB+ ∠EBA = 180°
∵∠DAB =80°,
∴ ∠EBA = 100 °.
∴ ∠ABC=∠ABE-∠CBE
=100°-40°=60°
∵ ∠CAB = ∠DAB-∠DAC
=80°-50°=30°
∴∠ACB =
180°
- ∠CAB - ∠ABC
= 180° - 30 ° - 60 °
=90°
2
1
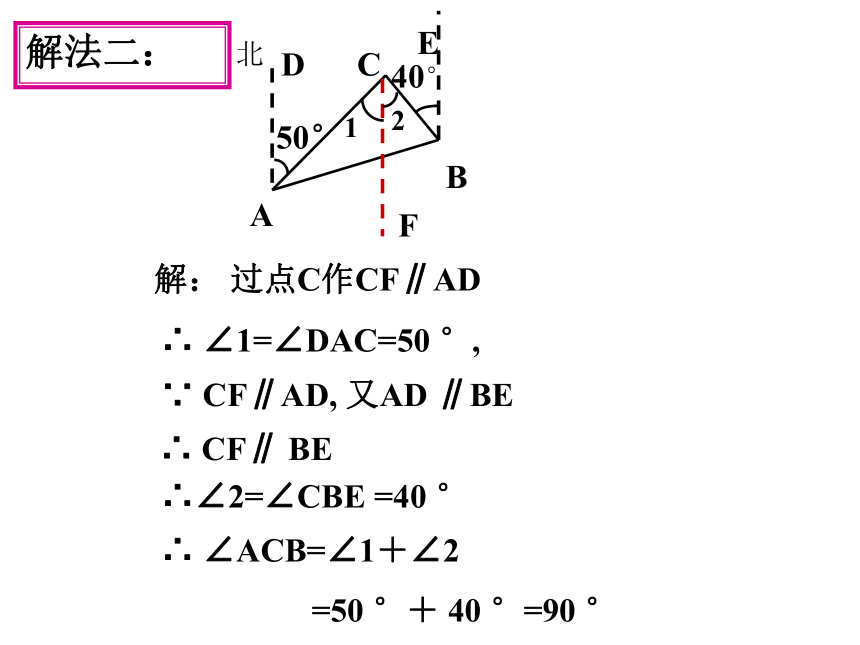
解法二:
B
D
C
E
北
A
50°
40°
解: 过点C作CF∥AD
F
∵ CF∥AD, 又AD ∥BE
∴ CF∥ BE
∴∠2=∠CBE =40 °
∴ ∠ACB=∠1+∠2
=50 °+ 40 °=90 °
∴ ∠1=∠DAC=50 °,
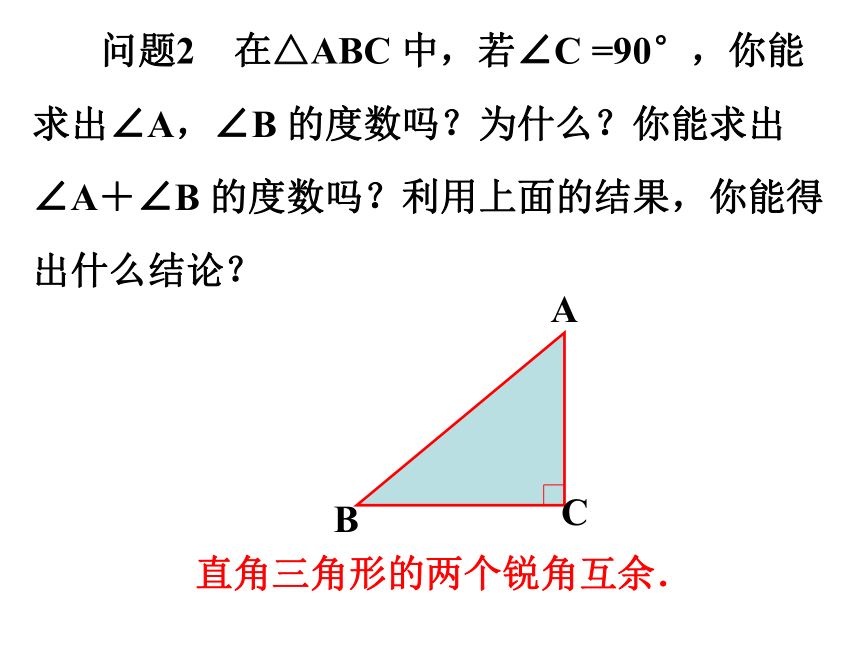
问题2 在△ABC 中,若∠C =90°,你能求出∠A,∠B 的度数吗?为什么?你能求出∠A+∠B 的度数吗?利用上面的结果,你能得出什么结论?
直角三角形的两个锐角互余.
C
A
B
直角三角形可以用符号“Rt△”表示,
直角三角形ABC 可以写成Rt△ABC .
C
A
B
在Rt△ABC 中,
∵∠C =90°,
∴∠A+∠B =90°.
直角三角形的两个锐角互余.
探索直角三角形的性质
学习新知
练习 如图,∠ACB =90°,CD⊥AB,垂足为D,
∠ACD 与∠B 有什么关系?为什么?
D
A
B
C
答:∠ACD =∠B 。
理由如下:
∵ ∠ACB =90°,
∴ ∠A+∠B = 90 °
∵CD ⊥AB,
∴ ∠CDA= 90 °
∴ ∠A+∠ACD = 90 °
∴ ∠ACD = ∠B
巩固新知
例 如图,∠C=∠D=90°,AD,BC 相交于点E, ∠CAE 与∠DBE 有什么关系?为什么?
分析:两个角的关系是什么?
这两个角分别在什么三角形中?
你如何验证自己的想法?
C
D
E
A
B
典型例析
解:在Rt△AEC 中,∵∠C =90°,
∴∠CAE+∠AEC =90°
在Rt△BDE 中,∵∠D =90°,
∴∠DBE+∠BED=90°
又∵ ∠AEC=∠BED
∴ ∠CAE=∠DBE
C
D
E
A
B
例 如图,∠C =∠D =90°,AD,BC 相交于点E,
∠CAE 与∠DBE 有什么关系?为什么?
(直角三角形两锐角互余).
(直角三角形两锐角互余).
(对顶角相等)
我们知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,你能得出什么结论?这个结论成立吗?如何验证你的想法?
∴△ABC 是直角三角形.
C
A
B
∵∠A+∠B =90°,
∴ ∠C = 180°-(∠A+∠B)
学习新知
探索直角三角形的判定
= 180°-90 °
= 90 °
推理格式:
在Rt△ABC 中,
∵∠A+∠B =90°,
∴△ABC是直角三角形.
A
B
C
有两个角互余的三角形是直角三角形.
直角三角形的判定:
1.在Rt△ABC中, 锐角∠A=25°,则另一个
锐角∠A 的度数是( ).
45° B. 65° C. 75° D. 55°
B
巩固新知
2.在△ABC中, 若∠A=∠C-∠B, 则
△ABC是( ).
锐角三角形 B. 钝角三角形
C. 直角三角形 D. 等腰三角形
C
3.如图, △ABC中,∠B=30°, ∠C=70°,
AD平分∠BAC,交BC于点F,DEBC于点E.
则 ∠D的度数是 .
20°
A
B
C
D
E
F
练习 如图,∠ACB =90°,CD⊥AB,垂足为D,
∠ACD 与∠B 有什么关系?为什么?
D
A
B
C
答:∠ACD =∠B .
理由如下:
∵∠ACB =90°,
∴ ∠A+ ∠B = 90 °.
∵CD ⊥AB,
∴∠CDA= 90 °.
∴∠A+ ∠ACD = 90 °.
∴∠ACD = ∠B.
巩固新知
练习 如图,∠ACB =90°,CD⊥AB,垂足为D,
∠ACD 与∠B 有什么关系?为什么?
D
A
B
C
答:∠ACD =∠B .
理由如下:
∵∠ACB =90°,
∴∠ACD+∠BCD = 90 °.
∵CD⊥AB,
∴∠CDB= 90 °.
∴∠B+∠BCD = 90 °.
∴∠ACD = ∠B.
巩固新知
变式1 若∠ACD =∠B,∠ACB =90°,则CD 是△ACB 的高吗?为什么?
D
A
B
C
答:CD 是△ACB 的高。
∵∠A CB =90°,
∴ ∠A+ ∠B = 90 °.
又∵ ∠ACD = ∠B,
∴ ∠A+ ∠ACD = 90 °.
∴△ADC 是直角三角形.
∴CD ⊥AB,
∴CD 是△ACB 的高.
理由如下:
巩固新知
变式2 若∠ACD =∠B,CD ⊥AB,△ACB 是直角三角形吗?为什么?
D
A
B
C
理由如下:
答:△ACB 是直角三角形.
∴ ∠BCD+ ∠B = 90 °.
∴△ACB是直角三角形.
又∵ ∠ACD = ∠B,
∴∠BCD+ ∠ACD = 90 °.
∵CD ⊥AB,
∴ ∠CDB= 90 °.
即 ∠ACB = 90 °.
巩固新知
变式3 如图,若∠C =90°,∠AED =∠B,
△ADE 是直角三角形吗?为什么?
理由如下:
D
E
A
B
C
答:△ADE 是直角三角形.
∵∠C= 90°,
∴∠A+∠B = 90 °
∵∠AED =∠B ,
∴∠A+∠AED = 90 °
∴△ADE是直角三角形.
巩固新知
(1)本节课学习了哪些主要内容?
(2)你是如何探索直角三角形的性质与判定的?
它们是怎么叙述的?它们有什么区别与联系?
(3)利用直角三角形的性质与判定分别可以解决哪些
问题?
今天你学到了什么?
课堂小结
今天作业
课本P16页第4 题
课本P17页第7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
11.2.1 三角形的内角(2)
复习旧知
三角形内角和定理:
三角形内角和等于180°.
1.如图,在△ABC 中,若∠A =60°,∠B =50°,则∠C = °.
2.如图,在△ABC 中, DE ∥ BC,若∠B =60°,∠AED =40°,则∠A = °.
A
B
C
B
C
A
D
E
70
80
例2 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从B岛看A 、 C两岛的视角∠ ABC是多少度 从C岛看A 、 B两岛的视角∠ ACB呢
A
D
B
C
E
北
北
【分析】直接写出下列各度数
∠DAC= ,
∠DAB= , ∠EBC= ,
∠CAB = .
50°
80°
40°
50°
80°
40°
30°
例2 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从B岛看A 、 C两岛的视角∠ ABC是多少度 从C岛看A 、 B两岛的视角∠ ACB呢
A
D
B
C
E
北
北
要求:∠EBA
要求:∠CBA、
要求:∠ACB
∠ABC
例2 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从B岛看A 、 C两岛的视角∠ ABC是多少度 从C岛看A 、 B两岛的视角∠ ACB呢
A
D
B
C
E
北
北
解:∵ AD∥BE,
∴ ∠DAB+ ∠EBA = 180°
∵∠DAB =80°,
∴ ∠EBA = 100 °.
∴ ∠ABC=∠ABE-∠CBE
=100°-40°=60°
∵ ∠CAB = ∠DAB-∠DAC
=80°-50°=30°
∴∠ACB =
180°
- ∠CAB - ∠ABC
= 180° - 30 ° - 60 °
=90°
2
1
解法二:
B
D
C
E
北
A
50°
40°
解: 过点C作CF∥AD
F
∵ CF∥AD, 又AD ∥BE
∴ CF∥ BE
∴∠2=∠CBE =40 °
∴ ∠ACB=∠1+∠2
=50 °+ 40 °=90 °
∴ ∠1=∠DAC=50 °,
问题2 在△ABC 中,若∠C =90°,你能求出∠A,∠B 的度数吗?为什么?你能求出∠A+∠B 的度数吗?利用上面的结果,你能得出什么结论?
直角三角形的两个锐角互余.
C
A
B
直角三角形可以用符号“Rt△”表示,
直角三角形ABC 可以写成Rt△ABC .
C
A
B
在Rt△ABC 中,
∵∠C =90°,
∴∠A+∠B =90°.
直角三角形的两个锐角互余.
探索直角三角形的性质
学习新知
练习 如图,∠ACB =90°,CD⊥AB,垂足为D,
∠ACD 与∠B 有什么关系?为什么?
D
A
B
C
答:∠ACD =∠B 。
理由如下:
∵ ∠ACB =90°,
∴ ∠A+∠B = 90 °
∵CD ⊥AB,
∴ ∠CDA= 90 °
∴ ∠A+∠ACD = 90 °
∴ ∠ACD = ∠B
巩固新知
例 如图,∠C=∠D=90°,AD,BC 相交于点E, ∠CAE 与∠DBE 有什么关系?为什么?
分析:两个角的关系是什么?
这两个角分别在什么三角形中?
你如何验证自己的想法?
C
D
E
A
B
典型例析
解:在Rt△AEC 中,∵∠C =90°,
∴∠CAE+∠AEC =90°
在Rt△BDE 中,∵∠D =90°,
∴∠DBE+∠BED=90°
又∵ ∠AEC=∠BED
∴ ∠CAE=∠DBE
C
D
E
A
B
例 如图,∠C =∠D =90°,AD,BC 相交于点E,
∠CAE 与∠DBE 有什么关系?为什么?
(直角三角形两锐角互余).
(直角三角形两锐角互余).
(对顶角相等)
我们知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,你能得出什么结论?这个结论成立吗?如何验证你的想法?
∴△ABC 是直角三角形.
C
A
B
∵∠A+∠B =90°,
∴ ∠C = 180°-(∠A+∠B)
学习新知
探索直角三角形的判定
= 180°-90 °
= 90 °
推理格式:
在Rt△ABC 中,
∵∠A+∠B =90°,
∴△ABC是直角三角形.
A
B
C
有两个角互余的三角形是直角三角形.
直角三角形的判定:
1.在Rt△ABC中, 锐角∠A=25°,则另一个
锐角∠A 的度数是( ).
45° B. 65° C. 75° D. 55°
B
巩固新知
2.在△ABC中, 若∠A=∠C-∠B, 则
△ABC是( ).
锐角三角形 B. 钝角三角形
C. 直角三角形 D. 等腰三角形
C
3.如图, △ABC中,∠B=30°, ∠C=70°,
AD平分∠BAC,交BC于点F,DEBC于点E.
则 ∠D的度数是 .
20°
A
B
C
D
E
F
练习 如图,∠ACB =90°,CD⊥AB,垂足为D,
∠ACD 与∠B 有什么关系?为什么?
D
A
B
C
答:∠ACD =∠B .
理由如下:
∵∠ACB =90°,
∴ ∠A+ ∠B = 90 °.
∵CD ⊥AB,
∴∠CDA= 90 °.
∴∠A+ ∠ACD = 90 °.
∴∠ACD = ∠B.
巩固新知
练习 如图,∠ACB =90°,CD⊥AB,垂足为D,
∠ACD 与∠B 有什么关系?为什么?
D
A
B
C
答:∠ACD =∠B .
理由如下:
∵∠ACB =90°,
∴∠ACD+∠BCD = 90 °.
∵CD⊥AB,
∴∠CDB= 90 °.
∴∠B+∠BCD = 90 °.
∴∠ACD = ∠B.
巩固新知
变式1 若∠ACD =∠B,∠ACB =90°,则CD 是△ACB 的高吗?为什么?
D
A
B
C
答:CD 是△ACB 的高。
∵∠A CB =90°,
∴ ∠A+ ∠B = 90 °.
又∵ ∠ACD = ∠B,
∴ ∠A+ ∠ACD = 90 °.
∴△ADC 是直角三角形.
∴CD ⊥AB,
∴CD 是△ACB 的高.
理由如下:
巩固新知
变式2 若∠ACD =∠B,CD ⊥AB,△ACB 是直角三角形吗?为什么?
D
A
B
C
理由如下:
答:△ACB 是直角三角形.
∴ ∠BCD+ ∠B = 90 °.
∴△ACB是直角三角形.
又∵ ∠ACD = ∠B,
∴∠BCD+ ∠ACD = 90 °.
∵CD ⊥AB,
∴ ∠CDB= 90 °.
即 ∠ACB = 90 °.
巩固新知
变式3 如图,若∠C =90°,∠AED =∠B,
△ADE 是直角三角形吗?为什么?
理由如下:
D
E
A
B
C
答:△ADE 是直角三角形.
∵∠C= 90°,
∴∠A+∠B = 90 °
∵∠AED =∠B ,
∴∠A+∠AED = 90 °
∴△ADE是直角三角形.
巩固新知
(1)本节课学习了哪些主要内容?
(2)你是如何探索直角三角形的性质与判定的?
它们是怎么叙述的?它们有什么区别与联系?
(3)利用直角三角形的性质与判定分别可以解决哪些
问题?
今天你学到了什么?
课堂小结
今天作业
课本P16页第4 题
课本P17页第7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
