11.2.2 三角形的外角 课件(共27张PPT)
文档属性
| 名称 | 11.2.2 三角形的外角 课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 09:31:13 | ||
图片预览


文档简介
(共27张PPT)
人教版 八年级上册
11.2.2 三角形的外角
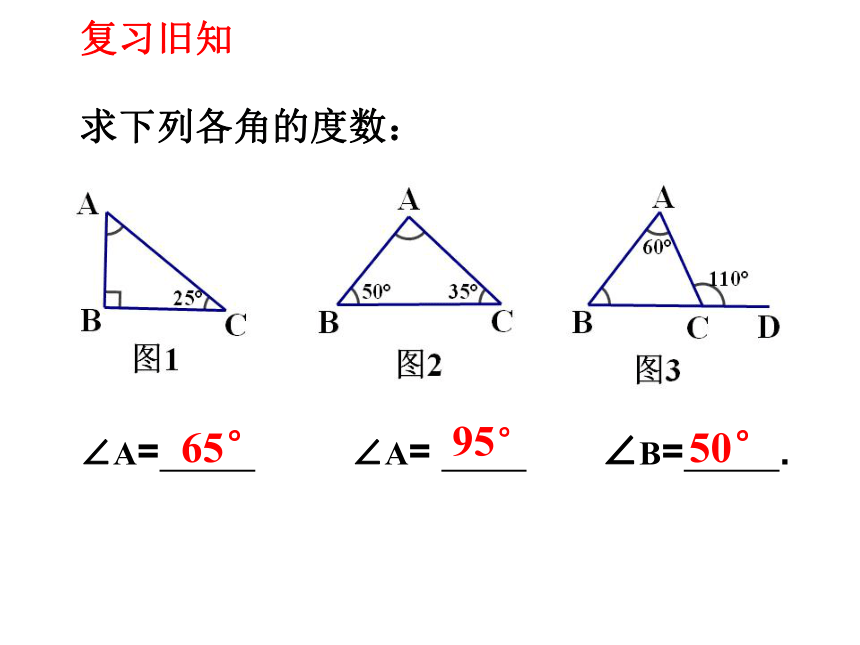
∠A= ∠A= ∠B= .
求下列各角的度数:
65°
95°
50°
复习旧知
A
B
C
D
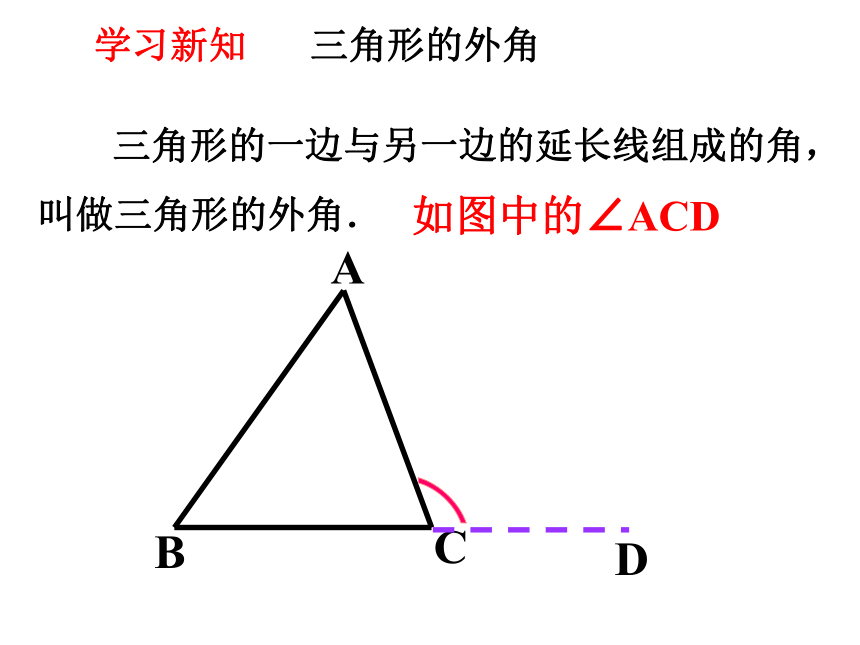
三角形的外角
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
学习新知
如图中的∠ACD
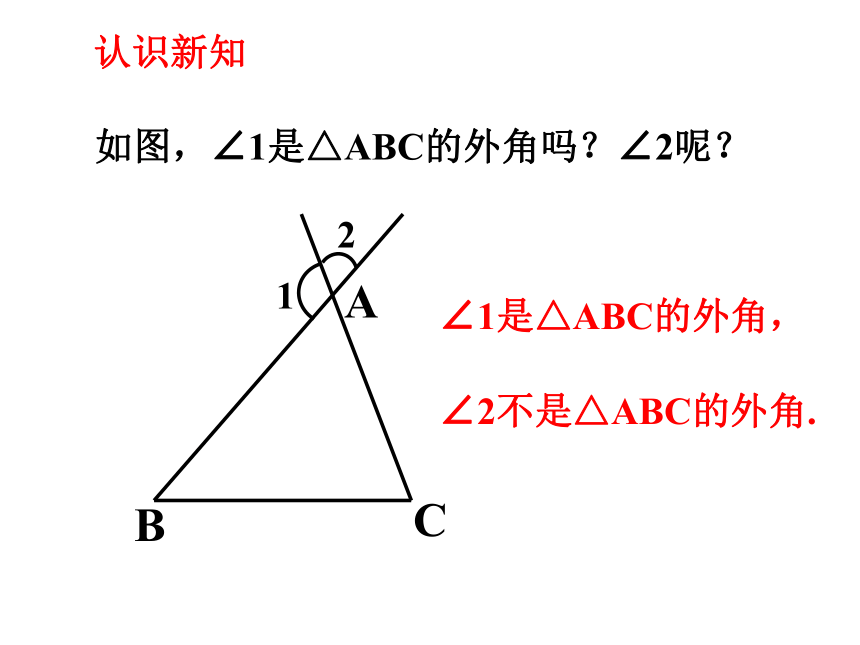
如图,∠1是△ABC的外角吗?∠2呢?
认识新知
A
B
C
2
1
∠1是△ABC的外角,
∠2不是△ABC的外角.
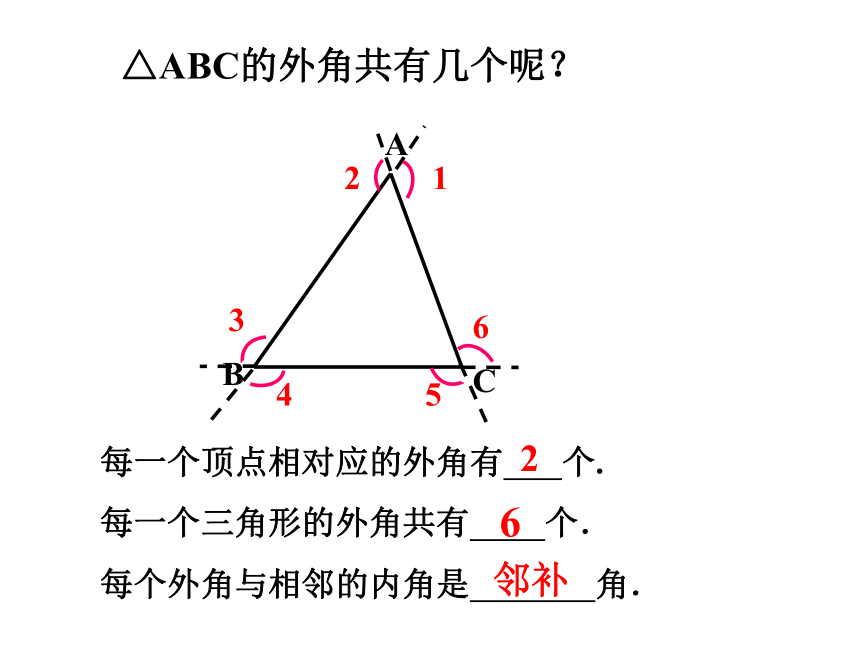
△ABC的外角共有几个呢?
每一个顶点相对应的外角有 个.
每一个三角形的外角共有 个.
每个外角与相邻的内角是 角.
A
B
C
1
2
3
4
6
5
6
2
邻补
(3)若∠A=30°,∠ B=70 ,
则∠1= °
(2)若∠A=40°,∠ B=80 ,
则∠1= °
(1)若∠A=50°,∠ B=60 ,
则∠1= °
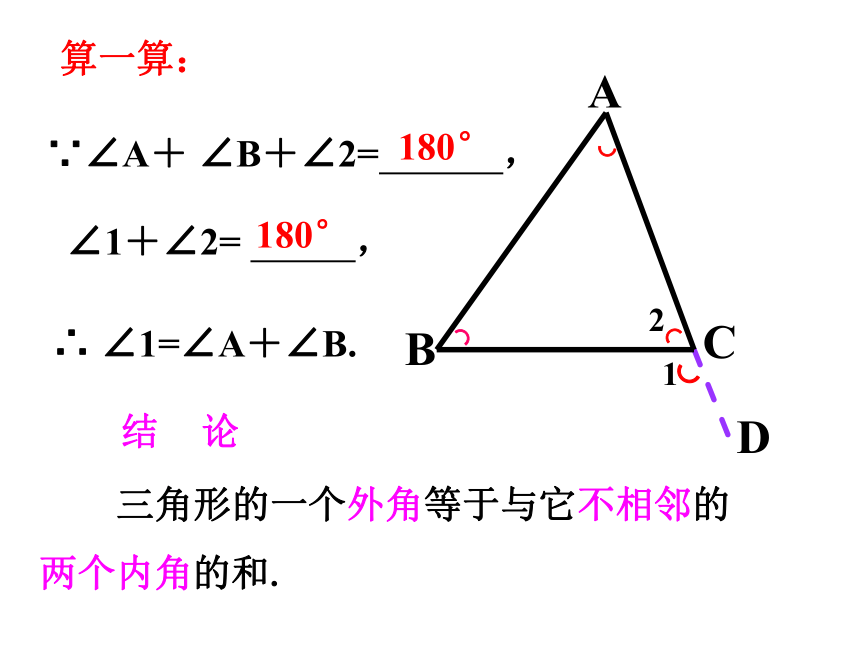
算一算:
1
2
A
B
C
D
⌒
⌒
⌒
⌒
110
120
100
∵∠A+ ∠B+∠2= ,
∠1+∠2= ,
算一算:
1
2
A
B
C
D
⌒
⌒
⌒
⌒
结 论
三角形的一个外角等于与它不相邻的
两个内角的和.
180°
180°
∴ ∠1=∠A+∠B.
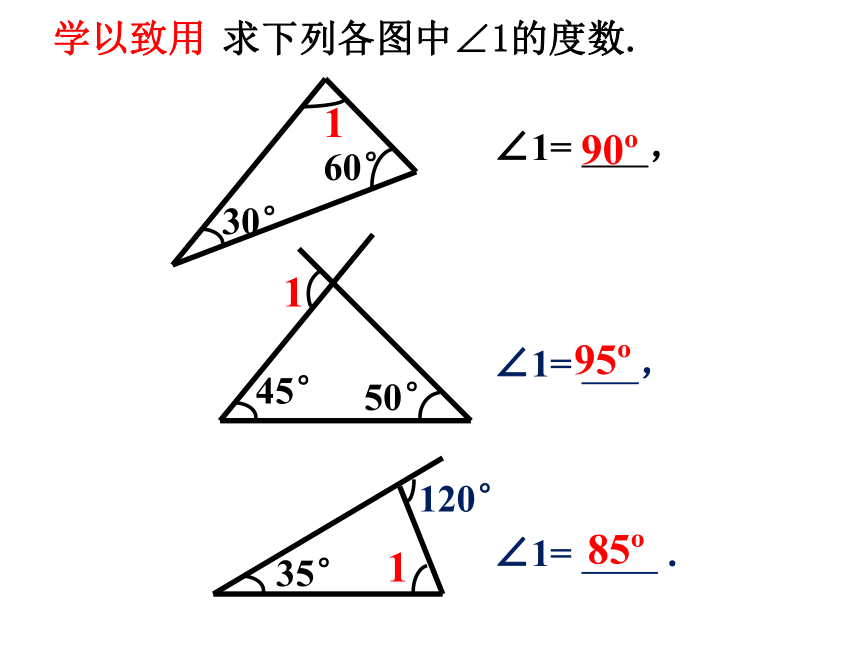
求下列各图中∠1的度数.
30°
60°
1
35°
120°
1
45°
50°
1
∠1= ,
∠1= ,
∠1= .
90
85
95
学以致用
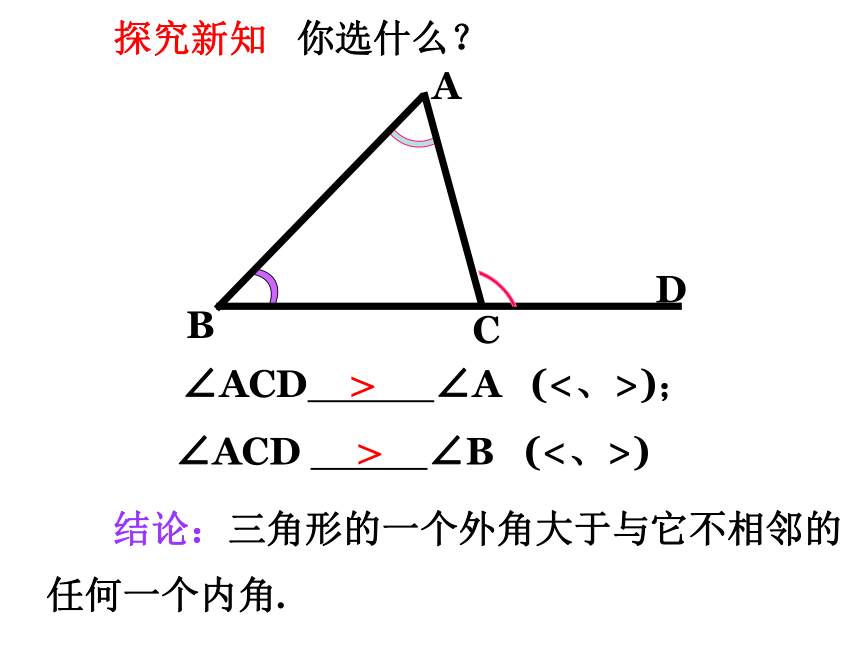
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
结论:三角形的一个外角大于与它不相邻的任何一个内角.
D
A
C
B
>
>
你选什么?
探究新知
B
3
2
1
A
C
D
E
2
1
2
1
2
1
2
1
1.下面四个图形中,能判断∠1>∠2 的是( )
A
B
C
D
D
2.把图中∠1、 ∠2、 ∠3按由大到小的顺序排列.
∠1
>
∠2
>
∠3
A
B
C
1
2
3
如图,∠1+∠2 +∠3 =
议一议
探究新知
A
B
C
1
2
3
∠2= +∠6
∠3= +∠5
∴由①+②+③,得:
∠1+ ∠2+ ∠3= 2(∠4+ ∠5+∠6)
∵∠4+ ∠5+∠6= °
∴∠1+∠2+∠3 =2×180°
∠1= +∠6
∴
4
5
6
①
③
②
180
=360°.
解: ∵ ∠1、 ∠2、 ∠3是△ABC的外角
∠5
∠4
∠4
结论:三角形的外角和=360°.
1.三角形的外角和是指三角形所有外角的和.( )
2.三角形的外角和等于它内角和的2倍. ( )
3.三角形的一个外角等于两个内角的和.( )
4.三角形的一个外角等于与它不相邻的两个内角的和.( )
5.三角形的一个外角大于任何一个内角.( )
6.三角形的一个内角小于任何一个与它不相邻的外角.( )
判断题:
学习新知
解:∵AB∥CD, ∠A=42°
∴ = ∠A= 42°.
例1:如图,AB∥CD,∠A=42°,∠D= 48°,求∠C和∠1的度数.
∵ ∠1是△OCD的一个外角, ∠D=48°,
∠C
∴ ∠1 =∠C+∠D
=42°+48°
=90°.
O
A
B
C
1
D
典型例析
如图,AB∥CD,∠1=88°,∠D= 48°, 求∠C和∠A的度数.
O
解:∵ ∠1是△OCD的一个外角
∴ ∠1= ∠C + ∠D
∵ ∠1=88°, ∠D=48°
∴ ∠C= ∠1 -∠D =
∵AB∥CD
∴ ∠A= ∠C=40°
88°- 48°
=40°
(两直线平行,内错角相等)
O
A
B
C
1
D
学以致用
巩固新知
1.如图,△ABC 的外角是( ).
∠1 B. ∠2 C. ∠3 D. ∠4
A
B
C
2
1
3
4
C
2.如图, ∠ ACD=120°, ∠B=20°,则∠A
的度数是( ).
120° B. 90° C. 100° D. 30°
A
B
C
D
C
3.将一副三角板按如图所示的方式摆放在一起,则∠1的度数是( )
A.55° B. 65° C. 75° D. 85°
1
C
4.如图, ∠ACD是△ABC的外角,CE平分
∠ ACD.若∠A =60°, ∠B=40°,则
∠ECD的度数是( ).
40° B. 45° C. 50° D. 55°
C
A
B
C
D
E
5.如图,在△ABC中,则∠A= .
60°
A
B
C
D
x°
(x+10)°
(x+70)°
6.∠A+∠B+∠C+∠D+∠E= .
A
D
E
C
B
1
2
180°
N
M
∵ ∠1是△MCD的一个外角
∴ ∠1= ∠C + ∠D
∵ ∠2是△NBE的一个外角
∴ ∠2= ∠B + ∠D
∵∠3= ∠1,
∠4= ∠2,
∴ ∠3= ∠C + ∠D,
∠4= ∠B + ∠E
∵∠A+ ∠3+∠4= 180°
∴∠A+∠B+∠C+∠D+∠E=180° .
3
4
7.∠A+∠B+∠C+∠D+∠E+∠F= .
A
D
E
C
F
B
1
2
3
360°
N
P
M
8. AB//CD,∠B=23°,∠D=42°,求∠BED.
F
∵AB∥CD, ∠B=23°
∴∠ EFD = ∠B= 23°
∵ ∠BED是△EFD的一个外角, ∠D=42°
∴ ∠BED = ∠EFD + ∠D
= 23°+ 42°
= 65°
解:
延长BE交CD于F,
2.三角形外角的两条性质
① 三角形的一个外角等于与它不相邻的两个内角的和。
② 三角形的一个外角大于与它不相邻的任何一个内角。
3.三角形的外角和是360°
1.三角形外角的定义
课堂小结
今天作业
课本P17页第8、9、11 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
11.2.2 三角形的外角
∠A= ∠A= ∠B= .
求下列各角的度数:
65°
95°
50°
复习旧知
A
B
C
D
三角形的外角
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
学习新知
如图中的∠ACD
如图,∠1是△ABC的外角吗?∠2呢?
认识新知
A
B
C
2
1
∠1是△ABC的外角,
∠2不是△ABC的外角.
△ABC的外角共有几个呢?
每一个顶点相对应的外角有 个.
每一个三角形的外角共有 个.
每个外角与相邻的内角是 角.
A
B
C
1
2
3
4
6
5
6
2
邻补
(3)若∠A=30°,∠ B=70 ,
则∠1= °
(2)若∠A=40°,∠ B=80 ,
则∠1= °
(1)若∠A=50°,∠ B=60 ,
则∠1= °
算一算:
1
2
A
B
C
D
⌒
⌒
⌒
⌒
110
120
100
∵∠A+ ∠B+∠2= ,
∠1+∠2= ,
算一算:
1
2
A
B
C
D
⌒
⌒
⌒
⌒
结 论
三角形的一个外角等于与它不相邻的
两个内角的和.
180°
180°
∴ ∠1=∠A+∠B.
求下列各图中∠1的度数.
30°
60°
1
35°
120°
1
45°
50°
1
∠1= ,
∠1= ,
∠1= .
90
85
95
学以致用
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
结论:三角形的一个外角大于与它不相邻的任何一个内角.
D
A
C
B
>
>
你选什么?
探究新知
B
3
2
1
A
C
D
E
2
1
2
1
2
1
2
1
1.下面四个图形中,能判断∠1>∠2 的是( )
A
B
C
D
D
2.把图中∠1、 ∠2、 ∠3按由大到小的顺序排列.
∠1
>
∠2
>
∠3
A
B
C
1
2
3
如图,∠1+∠2 +∠3 =
议一议
探究新知
A
B
C
1
2
3
∠2= +∠6
∠3= +∠5
∴由①+②+③,得:
∠1+ ∠2+ ∠3= 2(∠4+ ∠5+∠6)
∵∠4+ ∠5+∠6= °
∴∠1+∠2+∠3 =2×180°
∠1= +∠6
∴
4
5
6
①
③
②
180
=360°.
解: ∵ ∠1、 ∠2、 ∠3是△ABC的外角
∠5
∠4
∠4
结论:三角形的外角和=360°.
1.三角形的外角和是指三角形所有外角的和.( )
2.三角形的外角和等于它内角和的2倍. ( )
3.三角形的一个外角等于两个内角的和.( )
4.三角形的一个外角等于与它不相邻的两个内角的和.( )
5.三角形的一个外角大于任何一个内角.( )
6.三角形的一个内角小于任何一个与它不相邻的外角.( )
判断题:
学习新知
解:∵AB∥CD, ∠A=42°
∴ = ∠A= 42°.
例1:如图,AB∥CD,∠A=42°,∠D= 48°,求∠C和∠1的度数.
∵ ∠1是△OCD的一个外角, ∠D=48°,
∠C
∴ ∠1 =∠C+∠D
=42°+48°
=90°.
O
A
B
C
1
D
典型例析
如图,AB∥CD,∠1=88°,∠D= 48°, 求∠C和∠A的度数.
O
解:∵ ∠1是△OCD的一个外角
∴ ∠1= ∠C + ∠D
∵ ∠1=88°, ∠D=48°
∴ ∠C= ∠1 -∠D =
∵AB∥CD
∴ ∠A= ∠C=40°
88°- 48°
=40°
(两直线平行,内错角相等)
O
A
B
C
1
D
学以致用
巩固新知
1.如图,△ABC 的外角是( ).
∠1 B. ∠2 C. ∠3 D. ∠4
A
B
C
2
1
3
4
C
2.如图, ∠ ACD=120°, ∠B=20°,则∠A
的度数是( ).
120° B. 90° C. 100° D. 30°
A
B
C
D
C
3.将一副三角板按如图所示的方式摆放在一起,则∠1的度数是( )
A.55° B. 65° C. 75° D. 85°
1
C
4.如图, ∠ACD是△ABC的外角,CE平分
∠ ACD.若∠A =60°, ∠B=40°,则
∠ECD的度数是( ).
40° B. 45° C. 50° D. 55°
C
A
B
C
D
E
5.如图,在△ABC中,则∠A= .
60°
A
B
C
D
x°
(x+10)°
(x+70)°
6.∠A+∠B+∠C+∠D+∠E= .
A
D
E
C
B
1
2
180°
N
M
∵ ∠1是△MCD的一个外角
∴ ∠1= ∠C + ∠D
∵ ∠2是△NBE的一个外角
∴ ∠2= ∠B + ∠D
∵∠3= ∠1,
∠4= ∠2,
∴ ∠3= ∠C + ∠D,
∠4= ∠B + ∠E
∵∠A+ ∠3+∠4= 180°
∴∠A+∠B+∠C+∠D+∠E=180° .
3
4
7.∠A+∠B+∠C+∠D+∠E+∠F= .
A
D
E
C
F
B
1
2
3
360°
N
P
M
8. AB//CD,∠B=23°,∠D=42°,求∠BED.
F
∵AB∥CD, ∠B=23°
∴∠ EFD = ∠B= 23°
∵ ∠BED是△EFD的一个外角, ∠D=42°
∴ ∠BED = ∠EFD + ∠D
= 23°+ 42°
= 65°
解:
延长BE交CD于F,
2.三角形外角的两条性质
① 三角形的一个外角等于与它不相邻的两个内角的和。
② 三角形的一个外角大于与它不相邻的任何一个内角。
3.三角形的外角和是360°
1.三角形外角的定义
课堂小结
今天作业
课本P17页第8、9、11 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
