11.3.2 多边形的内角和 课件(共27张PPT)
文档属性
| 名称 | 11.3.2 多边形的内角和 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 00:00:00 | ||
图片预览


文档简介
(共27张PPT)
人教版 九年级上册
11.3.2 多边形的内角和
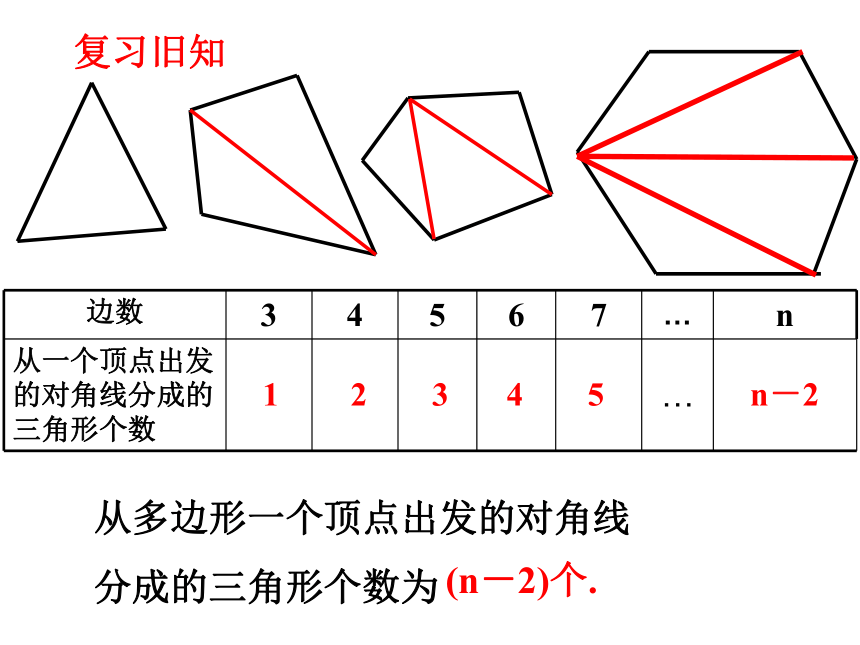
边数 3 4 5 6 7 … n
从一个顶点出发的对角线分成的三角形个数 …
1
2
3
4
5
n-2
从多边形一个顶点出发的对角线
分成的三角形个数为
(n-2)个.
复习旧知
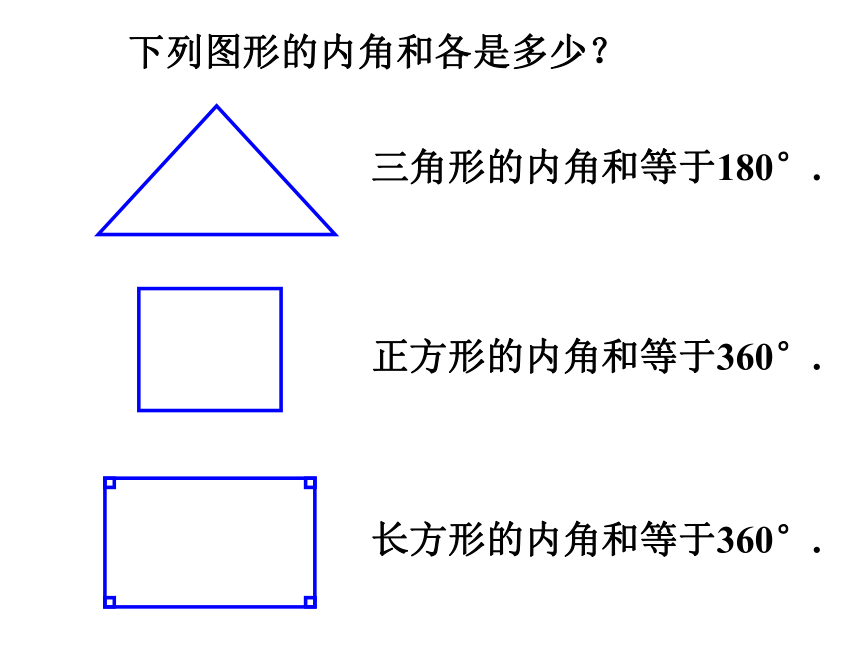
三角形的内角和等于180°.
下列图形的内角和各是多少?
正方形的内角和等于360°.
长方形的内角和等于360°.
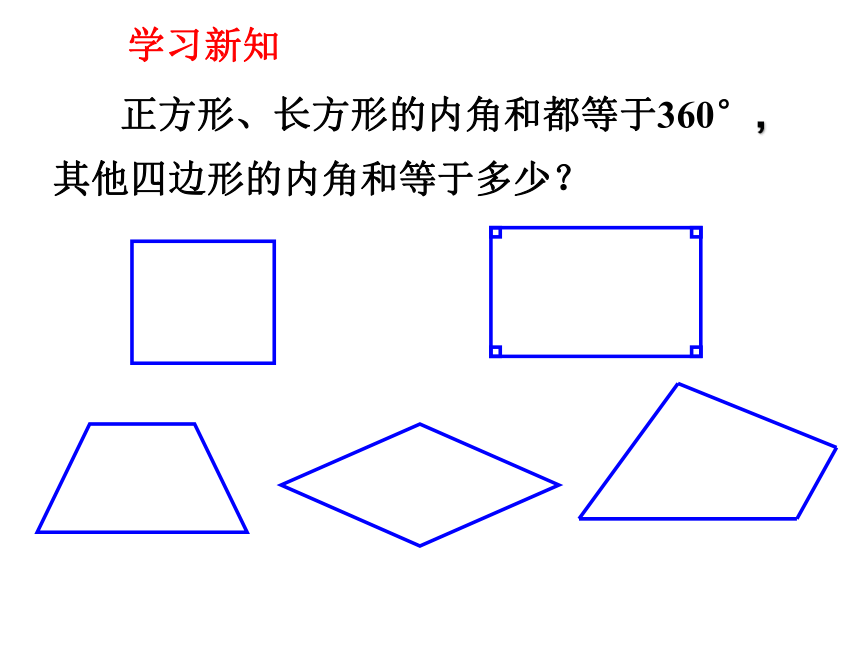
正方形、长方形的内角和都等于360°,其他四边形的内角和等于多少?
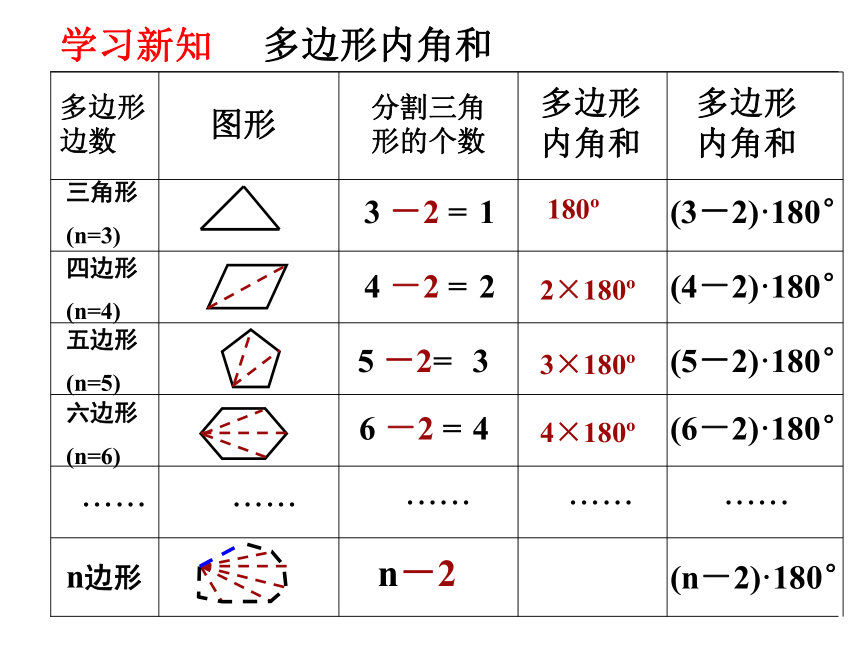
学习新知
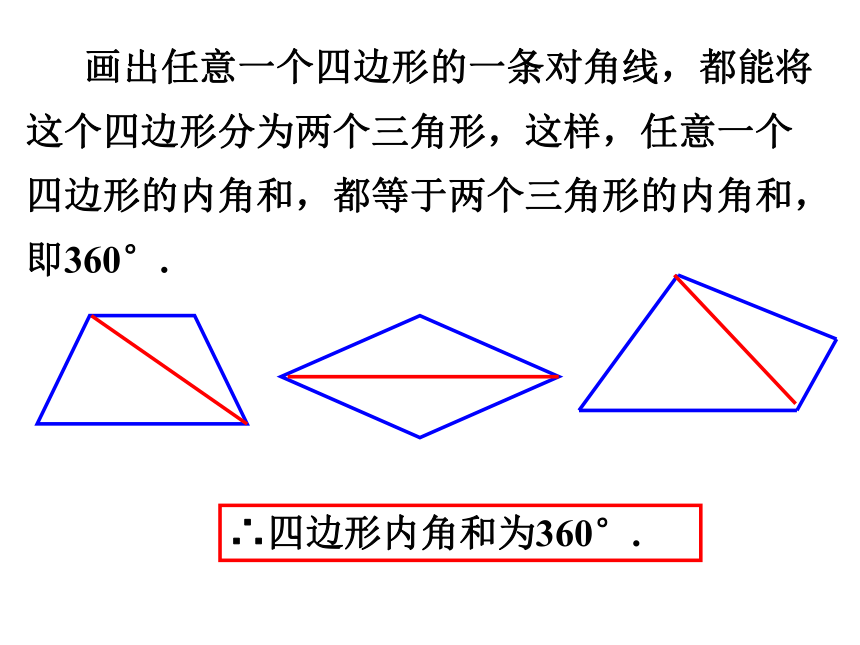
画出任意一个四边形的一条对角线,都能将这个四边形分为两个三角形,这样,任意一个四边形的内角和,都等于两个三角形的内角和,即360°.
∴四边形内角和为360°.
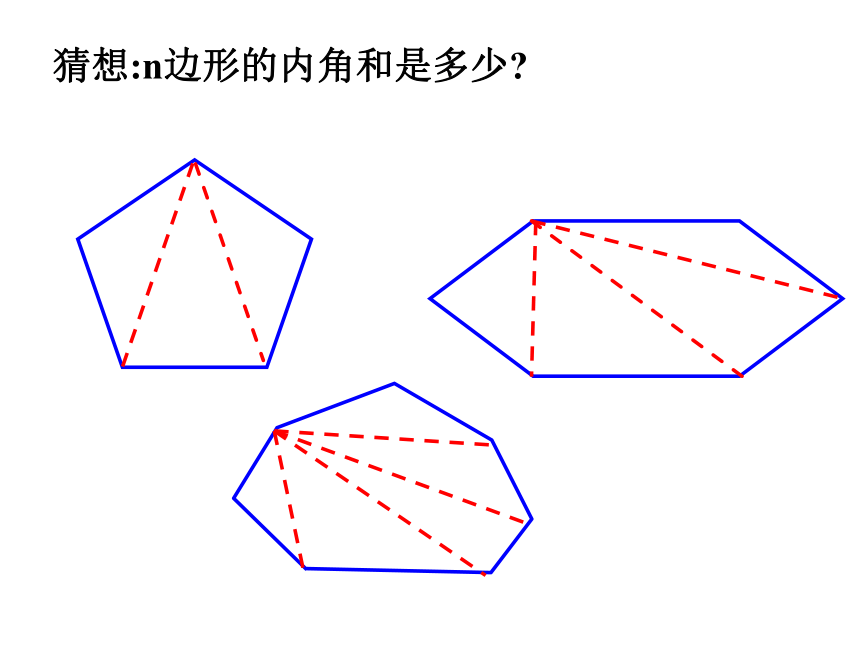
猜想:n边形的内角和是多少
多边形边数
图形
分割三角形的个数
多边形内角和
三角形
(n=3)
四边形
(n=4)
五边形
(n=5)
六边形
(n=6)
n边形
······
······
······
······
······
3 -2 =
1
4 -2 =
2
5 -2=
3
6 -2 =
4
n-2
2×180
180
3×180
4×180
(3-2)·180°
(4-2)·180°
(5-2)·180°
(6-2)·180°
(n-2)·180°
多边形内角和
学习新知
多边形内角和
n边形内角和等于(n-2)·180°
n边形内角和公式:
把一个多边形分成几个三角形,还有别的分法吗?由新的分法,能得出多边形内角和公式吗?
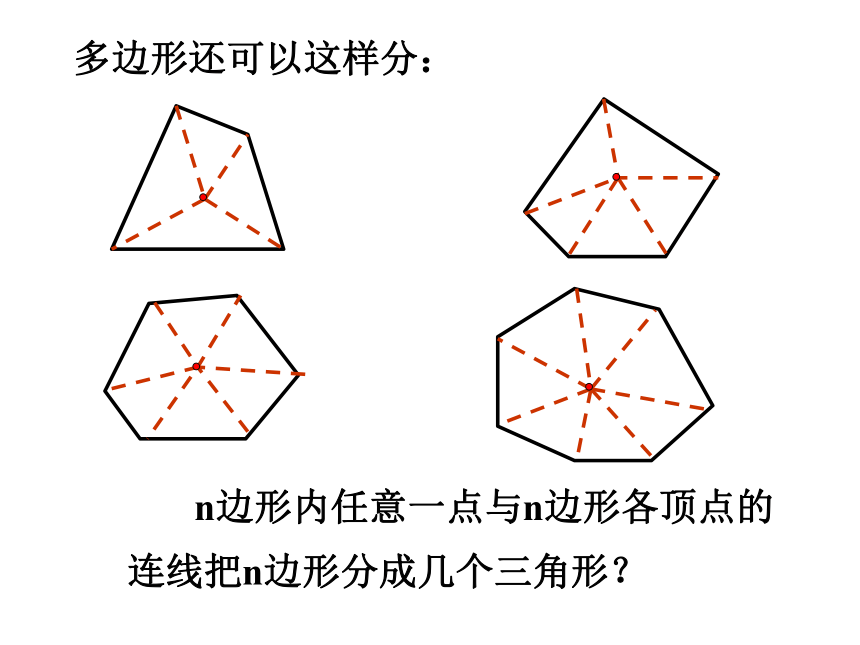
多边形还可以这样分:
n边形内任意一点与n边形各顶点的连线把n边形分成几个三角形?
E
A
B
C
D
O
180°×5
五边形内角和
– 360°=
(5-2)·180°
多边形边数
图形
分割三角形的个数
多边形内角和
四边形
(n=4)
五边形
(n=5)
六边形
(n=6)
n边形
······
······
······
······
······
4
5
6
7
n
(4-2)·180°
(5-2)·180°
(6-2)·180°
(7-2)·180°
(n-2)·180°
多边形内角和
180°×4
-360°
180°×5
-360°
180°×6
-360°
180°×7
-360°
180°×n
-360°
七边形
(n=7)
n边形内角和等于(n-2)·180°
3.一个多边形的内角和是720 ,则此多边形共有 个内角.
4.一个多边形当边数增加1时,它的内角和
增加 .
1.十二边形的内角和是 .
2.如果一个多边形的内角和是1440度,
那么这是 边形.
1800
180
六
十
巩固新知
在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.
4
2
6
5
1
3
D
E
B
F
C
A
六边形的外角和等于多少
∠1+∠2+∠3+∠4+∠5+∠6=
∵六边形的外角与相邻内角互补,
4
2
6
5
1
3
D
E
B
F
C
A
n边形的外角和呢?会是多少?
=6个平角
- 6边形内角和
=6×180°
-(6- 2) × 180°
=360 °
结论:六边形的外角和等于360°.
∴六边形的外角和
探究:在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
结论:n边形的外角和等于360°.
-(n-2) × 180°
=360 °
A
1
E
B
C
D
2
3
5
F
n
=n个平角-n边形内角和
=n×180 °
4
n边形的外角和等于多少?
任意多边形的外角和等于360 .
推论:
已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n,
∵它的内角和等于 (n-2) 180°,
它的外角和等于360 ,
∴ (n-2) 180°= .
解得: n=6
∴这个多边形的边数为6.
× 2
360
典型例析
(2)已知一个多边形的内角和为900° ,则这个多边形是____边形.
七
(1)十边形的内角和为_____,外角和为_____.
1440°
360°
巩固新知
(3)已知一个多边形的每一个外角都是72°,则这个多边形的边数为_____.
5
(4)在五边形ABCDE中,若∠A=∠D=90°,且∠B:∠C:∠E=3:2:4,则∠C的度数为_____.
80°
巩固新知
(5)如图,已知五边形ABCDE中,AB ∥ CD,则∠E的度数为_____.
A
B
C
D
E
150°
125°
85°
(6)如图,已知∠1,∠2,∠3,∠4是五边形ABCDE的外角,若∠A=120°,则∠1 + ∠2 + ∠3 + ∠4的度数为 _____ .
A
B
C
D
E
120°
1
2
3
4
300°
(7)如图,在四边形ABCD中,∠A+∠B
+∠C=260°,则∠D 的度数为 .
A
B
C
D
100°
(8)如图,已知∠1,∠2分别是四边形ABCD
的∠BCD和∠BAD的邻补角,若∠B+∠ADC
=140°,则∠1 + ∠2 的度数为 .
A
B
C
D
1
2
140°
9.如果一个凸多边形的所有内角从小到大排列起来,恰好依次增加的度数相同,设最小角为100°,最大角为140°,那么这个多边形的边数为多少?
解:设该多边形的边数为n. 则有
=180° (n - 2)
解得 ,n=6.
故这个多边形为六边形.
(100°+140°)n
2
1.n边形的内角和等于:
(n - 2) 180°.
2.n边形的外角和等于:
360°.
课堂小结
今天作业
课本P24页第4、5、6 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 九年级上册
11.3.2 多边形的内角和
边数 3 4 5 6 7 … n
从一个顶点出发的对角线分成的三角形个数 …
1
2
3
4
5
n-2
从多边形一个顶点出发的对角线
分成的三角形个数为
(n-2)个.
复习旧知
三角形的内角和等于180°.
下列图形的内角和各是多少?
正方形的内角和等于360°.
长方形的内角和等于360°.
正方形、长方形的内角和都等于360°,其他四边形的内角和等于多少?
学习新知
画出任意一个四边形的一条对角线,都能将这个四边形分为两个三角形,这样,任意一个四边形的内角和,都等于两个三角形的内角和,即360°.
∴四边形内角和为360°.
猜想:n边形的内角和是多少
多边形边数
图形
分割三角形的个数
多边形内角和
三角形
(n=3)
四边形
(n=4)
五边形
(n=5)
六边形
(n=6)
n边形
······
······
······
······
······
3 -2 =
1
4 -2 =
2
5 -2=
3
6 -2 =
4
n-2
2×180
180
3×180
4×180
(3-2)·180°
(4-2)·180°
(5-2)·180°
(6-2)·180°
(n-2)·180°
多边形内角和
学习新知
多边形内角和
n边形内角和等于(n-2)·180°
n边形内角和公式:
把一个多边形分成几个三角形,还有别的分法吗?由新的分法,能得出多边形内角和公式吗?
多边形还可以这样分:
n边形内任意一点与n边形各顶点的连线把n边形分成几个三角形?
E
A
B
C
D
O
180°×5
五边形内角和
– 360°=
(5-2)·180°
多边形边数
图形
分割三角形的个数
多边形内角和
四边形
(n=4)
五边形
(n=5)
六边形
(n=6)
n边形
······
······
······
······
······
4
5
6
7
n
(4-2)·180°
(5-2)·180°
(6-2)·180°
(7-2)·180°
(n-2)·180°
多边形内角和
180°×4
-360°
180°×5
-360°
180°×6
-360°
180°×7
-360°
180°×n
-360°
七边形
(n=7)
n边形内角和等于(n-2)·180°
3.一个多边形的内角和是720 ,则此多边形共有 个内角.
4.一个多边形当边数增加1时,它的内角和
增加 .
1.十二边形的内角和是 .
2.如果一个多边形的内角和是1440度,
那么这是 边形.
1800
180
六
十
巩固新知
在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.
4
2
6
5
1
3
D
E
B
F
C
A
六边形的外角和等于多少
∠1+∠2+∠3+∠4+∠5+∠6=
∵六边形的外角与相邻内角互补,
4
2
6
5
1
3
D
E
B
F
C
A
n边形的外角和呢?会是多少?
=6个平角
- 6边形内角和
=6×180°
-(6- 2) × 180°
=360 °
结论:六边形的外角和等于360°.
∴六边形的外角和
探究:在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
结论:n边形的外角和等于360°.
-(n-2) × 180°
=360 °
A
1
E
B
C
D
2
3
5
F
n
=n个平角-n边形内角和
=n×180 °
4
n边形的外角和等于多少?
任意多边形的外角和等于360 .
推论:
已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n,
∵它的内角和等于 (n-2) 180°,
它的外角和等于360 ,
∴ (n-2) 180°= .
解得: n=6
∴这个多边形的边数为6.
× 2
360
典型例析
(2)已知一个多边形的内角和为900° ,则这个多边形是____边形.
七
(1)十边形的内角和为_____,外角和为_____.
1440°
360°
巩固新知
(3)已知一个多边形的每一个外角都是72°,则这个多边形的边数为_____.
5
(4)在五边形ABCDE中,若∠A=∠D=90°,且∠B:∠C:∠E=3:2:4,则∠C的度数为_____.
80°
巩固新知
(5)如图,已知五边形ABCDE中,AB ∥ CD,则∠E的度数为_____.
A
B
C
D
E
150°
125°
85°
(6)如图,已知∠1,∠2,∠3,∠4是五边形ABCDE的外角,若∠A=120°,则∠1 + ∠2 + ∠3 + ∠4的度数为 _____ .
A
B
C
D
E
120°
1
2
3
4
300°
(7)如图,在四边形ABCD中,∠A+∠B
+∠C=260°,则∠D 的度数为 .
A
B
C
D
100°
(8)如图,已知∠1,∠2分别是四边形ABCD
的∠BCD和∠BAD的邻补角,若∠B+∠ADC
=140°,则∠1 + ∠2 的度数为 .
A
B
C
D
1
2
140°
9.如果一个凸多边形的所有内角从小到大排列起来,恰好依次增加的度数相同,设最小角为100°,最大角为140°,那么这个多边形的边数为多少?
解:设该多边形的边数为n. 则有
=180° (n - 2)
解得 ,n=6.
故这个多边形为六边形.
(100°+140°)n
2
1.n边形的内角和等于:
(n - 2) 180°.
2.n边形的外角和等于:
360°.
课堂小结
今天作业
课本P24页第4、5、6 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
