第11章 三角形 小结 课件(共34张PPT)
文档属性
| 名称 | 第11章 三角形 小结 课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 15:51:02 | ||
图片预览







文档简介
(共34张PPT)
人教版 九年级上册
第11章 三角形 小结
请回答下列问题:
(1)三角形的三边之间有怎样的关系?得出这个结论的依据是什么?
三角形两边的和大于第三边.
三角形两边的差小于第三边.
三角形两边的差
第三边
三角形两边的和
<
<
两点之间,线段最短.
这个结论的依据是线段公理:
请回答下列问题:
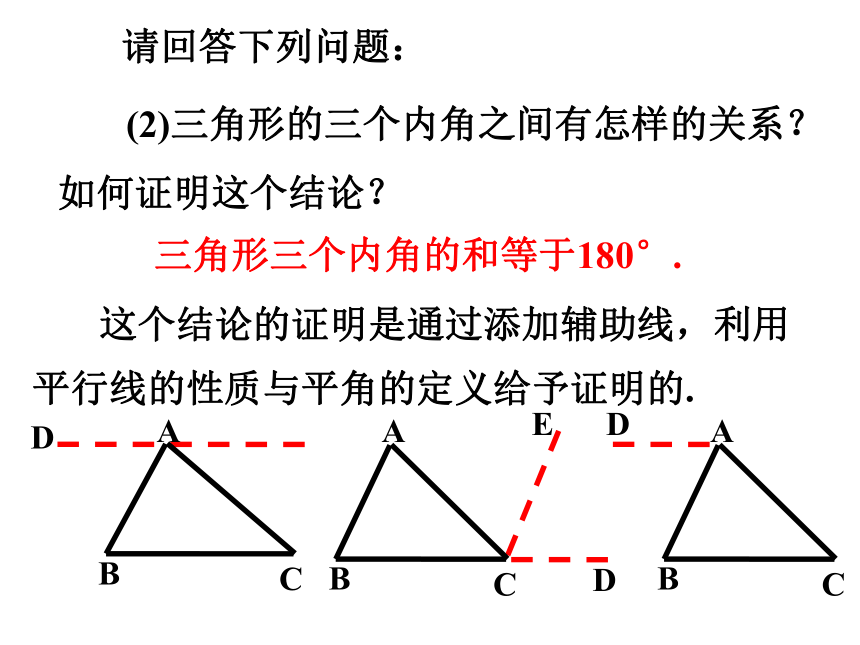
(2)三角形的三个内角之间有怎样的关系?如何证明这个结论?
三角形三个内角的和等于180°.
这个结论的证明是通过添加辅助线,利用
平行线的性质与平角的定义给予证明的.
E
D
C
B
A
C
B
A
C
B
A
D
D
请回答下列问题:
(3) 直角三角形的两个锐角之间有怎样的关系?
直角三角形的两个锐角互余.
C
A
B
在Rt△ABC 中,
∵∠C =90°,
∴∠A +∠B =90°.
请回答下列问题:
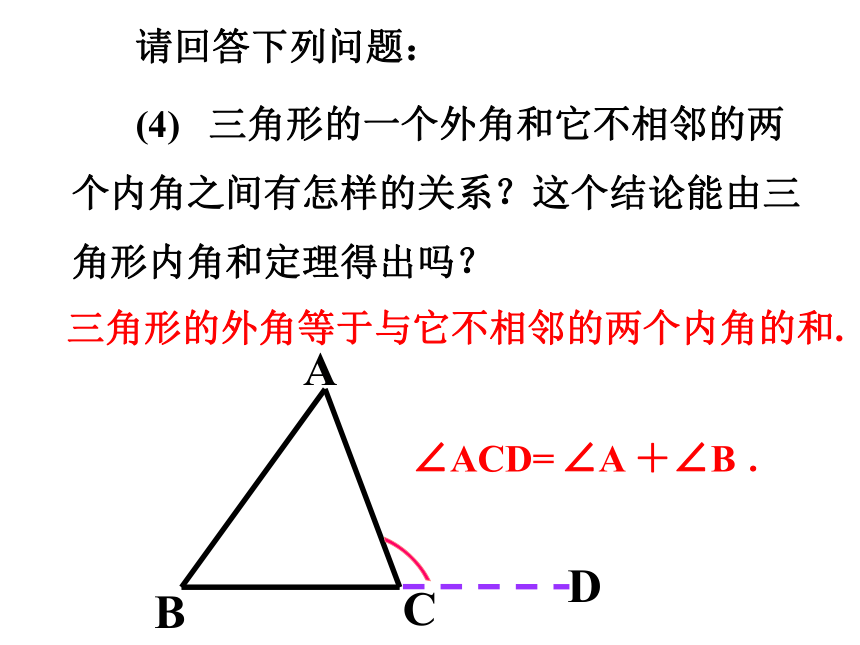
(4) 三角形的一个外角和它不相邻的两个内角之间有怎样的关系?这个结论能由三角形内角和定理得出吗?
三角形的外角等于与它不相邻的两个内角的和.
A
B
C
D
∠A +∠B .
∠ACD=
请回答下列问题:
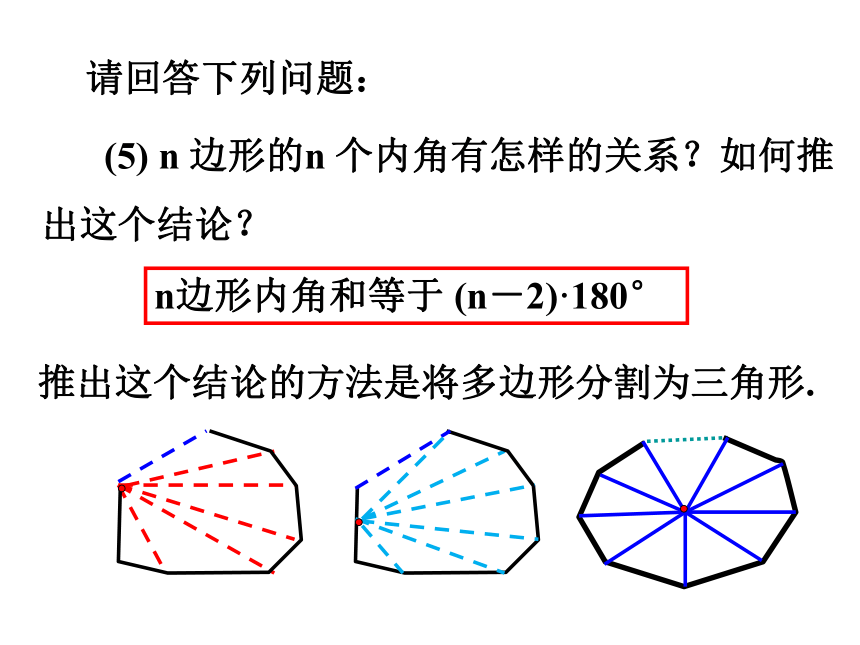
(5) n 边形的n 个内角有怎样的关系?如何推出这个结论?
n边形内角和等于 (n-2)·180°
推出这个结论的方法是将多边形分割为三角形.
请回答下列问题:
(6)n 边形的外角和与n 有关吗?为什么?
n 边形的外角和与n 没有关系.
因为任意多边形的外角和都是360°.
例1 已知等腰三角形的两边长分别为10 和6 ,则三角形的周长是 .
变式1 若等腰三角形的周长为20,一边长为4,则其他两边长为 .
22
8和8
或26
典型例题
变式2 小明用一条长20 cm的细绳围成了一个等腰
三角形,他想使这个三角形的一边长是另一边长的2倍,
那么这个三角形的各边的长分别是多少?
解:设较短的边长为 x cm,
则较长的边长为2x cm.
若较短的边为腰,
则x + x + 2x =20.
解得 x =5.
即 2x =10.
∵5 + 5 =10,
∴不能围成腰长5cm的等腰三角形.
不符合三角形两边的和大于第三边,
变式3 小明用一条长20 cm的细绳围成了一个等腰
三角形,他想使这个三角形的一边长是另一边长的2倍,
那么这个三角形的各边的长分别是多少?
解:若较长的边为腰,则 x + 2x + 2x =20.
解得 x =4.
所以,这个三角形的三边分别为:
4 cm, 8 cm, 8 cm.
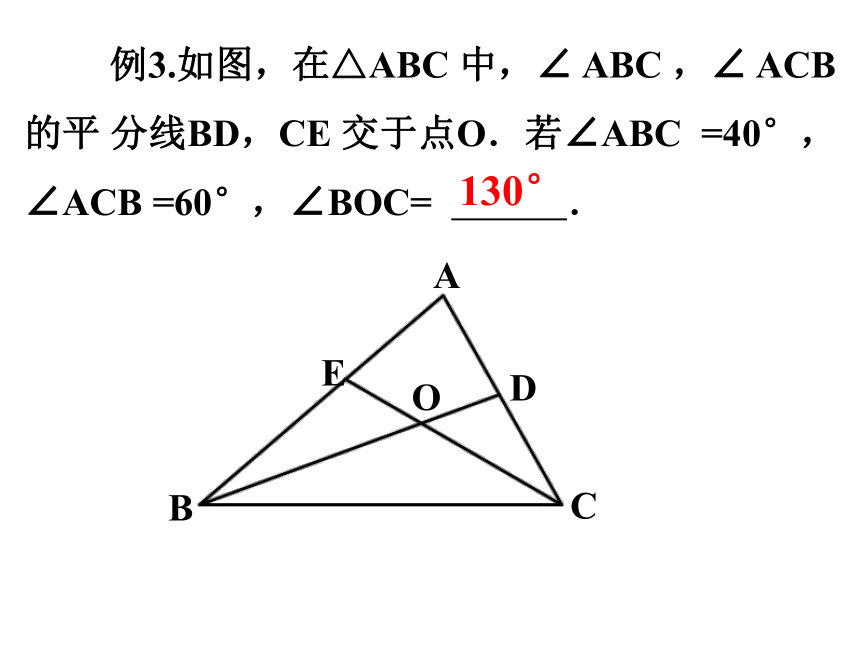
例3.如图,在△ABC 中,∠ ABC ,∠ ACB 的平 分线BD,CE 交于点O.若∠ABC =40°,∠ACB =60°,∠BOC= .
A
B
C
O
E
D
130°
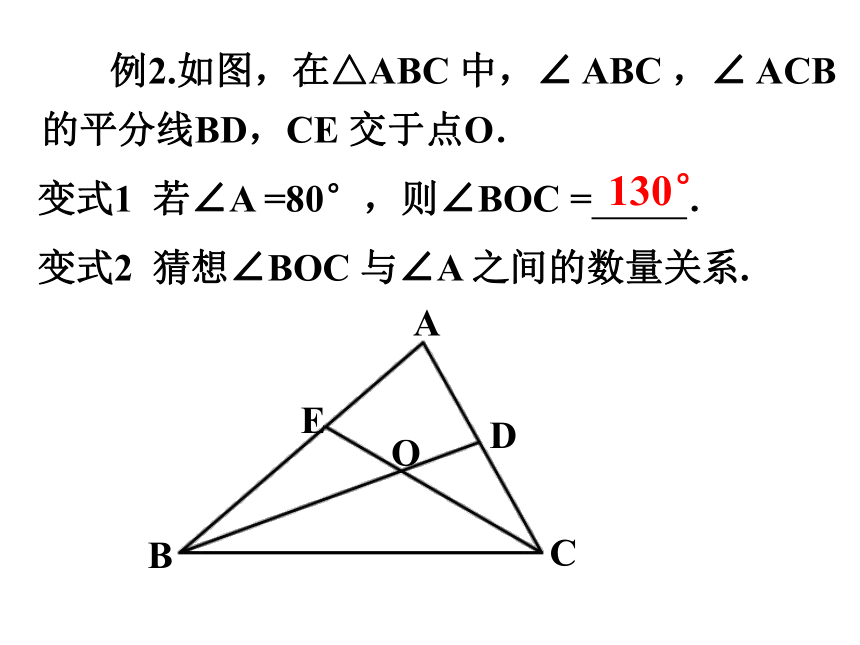
例2.如图,在△ABC 中,∠ ABC ,∠ ACB的平分线BD,CE 交于点O.
变式1 若∠A =80°,则∠BOC = .
变式2 猜想∠BOC 与∠A 之间的数量关系.
A
B
C
O
E
D
130°
A
B
C
O
E
D
例2 如图,在△ABC 中,∠ ABC ,∠ ACB 的平分线BD,CE 交于点O.则∠BOC 与∠A 之间有怎样的数量关系?
∵BD、CE分别是∠ABC、∠ACB的角平分线,
∴∠DBC =
∠ABC ,
1
2
∠ECB =
∠ACB ,
1
2
∵ ∠BOC = 180°-(∠DBC + ∠ECB)
∴ ∠BCD = 180°-( ∠ABC + ∠ACB)
1
2
1
2
= 180°- (∠ABC + ∠ACB)
1
2
= 180°- (180°- ∠A)
1
2
= 90°+ ∠A
1
2
几何模型之角平分线模型
α
A
B
C
O
(1)两内角角平分线型
∠A+90°
1
2
∠α=
变式3 如图,若换成两外角平分线相交于O,则∠BOC 与∠A 又有怎样的数量关系?
A
B
C
O
E
D
∵OB、OC分别是∠DBC、∠ECB的角平分线,
∴∠OBC =
∠DBC ,
1
2
∠OCB =
∠ECB ,
1
2
∵ ∠BOC = 180°-(∠OBC + ∠OCB)
∴ ∠BOC = 180°-( ∠DBC + ∠ECB)
= 180°- (∠DBC + ∠ECB)
= 180°- (∠A+∠ACB+∠ABC +∠A)
1
2
1
2
1
2
1
2
1
2
= 180°- (180°+∠A)
= 90°- ∠A
1
2
几何模型角平分线模型
α
O
B
C
A
90°- ∠A
1
2
∠α=
(2)两外角角平分线型
变式4 如图,若换成一内角与一外角平分线相交
于点O,则∠BOC与∠A 又有怎样的数量关系?
A
B
C
O
D
∵OB是∠ABC的角平分线,
∵OC是∠ACD的角平分线,
∴∠OBC =
∠ABC .
1
2
∴∠OCD =
∠ACD .
1
2
∵ ∠OCD = ∠OBC + ∠BOC,
∴ ∠BOC = ∠OCD - ∠OBC.
∵ ∠ACD = ∠ABC + ∠A,
∴ ∠BOC = (∠ABC + ∠A )
1
2
- ∠ABC
1
2
= ∠A.
1
2
几何模型之角平分线模型
(3)内外角角平分线型
α
A
B
C
O
D
∠A
1
2
∠α=
变式5 如图,若换成两条高相交于点O, ∠A 与∠BOC 又有怎样的数量关系?
A
B
C
O
E
D
∵BD、CE是△ ABC的高,
∴∠ ADB = ∠ AEC =90°.
∵∠A+∠AEC+∠EOD +∠ADO =360°,
∴ ∠A +∠EOD = 180°,
∴ ∠EOD = 180° - ∠A.
∵ ∠BOC = ∠EOD ,
∴ ∠EOD = 180° - ∠A.
1.列每组数分别表示三根木棒的长度,将它们首尾连结后,能摆成三角形的一组是( )
A.1,2,6 B.2,2,4
C.1,2,3 D.2,3,4
D
练习巩固
2.把一把直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为( )
A.120° B.125° C.130° D.140°
C
3.如图,一副分别含有30°和45°角的两个直角三角板,拼在一起,其中∠C=90°,∠B=45°, ∠E=30°,则∠BFD的度数是( )
A.10° B.25° C.30° D.15°
D
4.一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )
A.165° B.120° C.150° D.135°
A
5.如图,在△ABC中,AD是△ABC的角平分线,∠B=67°,∠C=33°,则∠CAD的度数为( )
A.40° B.45° C.50° D.55°
A
6.如图,∠1=100°,∠C=70°,则∠A的大小是( )
A.10° B.20° C.30° D.80°
第6题
C
7.若三角形的两边分别为3 和5 ,则第三边长m 的取值范围是 __________ .
<
<
m
8
2
8.如图,(1)若AD ⊥BC,垂足为D,则:∠_____ =∠_____ = 90°;
A
B
C
D
E
F
ADB
ADC
8.如图,(2)若∠BAE =∠CAE, AE 与BC 相交于点E,则:线段AE 是△ABC 的________;
角平分线
A
B
C
D
E
F
8.如图,(3)若AF =CF,BF 与 AC 相交于
点F,则:△ABC 的中线是 .
BF
A
B
C
D
E
F
9.如图,在△ABC 中,已知∠BAC =80°,∠ABC =60°.
(1)∠C = ;
(2)若AE 是△ABC 的
角平分线,则:
∠AEC = ;
(3)若BF 是△ABC 的高,与角平分线AE 相交于点O,则∠EOF = .
A
B
C
O
E
F
40°
100°
130°
10.如图,△ABC中,∠A=α,∠ABC
的平分线与∠ACD的平分线交与点A1,得∠A1 ,∠A1BC的平分线与∠A1CD的平分线交与点A2 ,得∠A2 ……,则∠A6与α的数量
关系是 .
A
B
C
A1
D
A2
∠A6=
1
64
∠α
今天作业
课本P29页第8、11、12 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 九年级上册
第11章 三角形 小结
请回答下列问题:
(1)三角形的三边之间有怎样的关系?得出这个结论的依据是什么?
三角形两边的和大于第三边.
三角形两边的差小于第三边.
三角形两边的差
第三边
三角形两边的和
<
<
两点之间,线段最短.
这个结论的依据是线段公理:
请回答下列问题:
(2)三角形的三个内角之间有怎样的关系?如何证明这个结论?
三角形三个内角的和等于180°.
这个结论的证明是通过添加辅助线,利用
平行线的性质与平角的定义给予证明的.
E
D
C
B
A
C
B
A
C
B
A
D
D
请回答下列问题:
(3) 直角三角形的两个锐角之间有怎样的关系?
直角三角形的两个锐角互余.
C
A
B
在Rt△ABC 中,
∵∠C =90°,
∴∠A +∠B =90°.
请回答下列问题:
(4) 三角形的一个外角和它不相邻的两个内角之间有怎样的关系?这个结论能由三角形内角和定理得出吗?
三角形的外角等于与它不相邻的两个内角的和.
A
B
C
D
∠A +∠B .
∠ACD=
请回答下列问题:
(5) n 边形的n 个内角有怎样的关系?如何推出这个结论?
n边形内角和等于 (n-2)·180°
推出这个结论的方法是将多边形分割为三角形.
请回答下列问题:
(6)n 边形的外角和与n 有关吗?为什么?
n 边形的外角和与n 没有关系.
因为任意多边形的外角和都是360°.
例1 已知等腰三角形的两边长分别为10 和6 ,则三角形的周长是 .
变式1 若等腰三角形的周长为20,一边长为4,则其他两边长为 .
22
8和8
或26
典型例题
变式2 小明用一条长20 cm的细绳围成了一个等腰
三角形,他想使这个三角形的一边长是另一边长的2倍,
那么这个三角形的各边的长分别是多少?
解:设较短的边长为 x cm,
则较长的边长为2x cm.
若较短的边为腰,
则x + x + 2x =20.
解得 x =5.
即 2x =10.
∵5 + 5 =10,
∴不能围成腰长5cm的等腰三角形.
不符合三角形两边的和大于第三边,
变式3 小明用一条长20 cm的细绳围成了一个等腰
三角形,他想使这个三角形的一边长是另一边长的2倍,
那么这个三角形的各边的长分别是多少?
解:若较长的边为腰,则 x + 2x + 2x =20.
解得 x =4.
所以,这个三角形的三边分别为:
4 cm, 8 cm, 8 cm.
例3.如图,在△ABC 中,∠ ABC ,∠ ACB 的平 分线BD,CE 交于点O.若∠ABC =40°,∠ACB =60°,∠BOC= .
A
B
C
O
E
D
130°
例2.如图,在△ABC 中,∠ ABC ,∠ ACB的平分线BD,CE 交于点O.
变式1 若∠A =80°,则∠BOC = .
变式2 猜想∠BOC 与∠A 之间的数量关系.
A
B
C
O
E
D
130°
A
B
C
O
E
D
例2 如图,在△ABC 中,∠ ABC ,∠ ACB 的平分线BD,CE 交于点O.则∠BOC 与∠A 之间有怎样的数量关系?
∵BD、CE分别是∠ABC、∠ACB的角平分线,
∴∠DBC =
∠ABC ,
1
2
∠ECB =
∠ACB ,
1
2
∵ ∠BOC = 180°-(∠DBC + ∠ECB)
∴ ∠BCD = 180°-( ∠ABC + ∠ACB)
1
2
1
2
= 180°- (∠ABC + ∠ACB)
1
2
= 180°- (180°- ∠A)
1
2
= 90°+ ∠A
1
2
几何模型之角平分线模型
α
A
B
C
O
(1)两内角角平分线型
∠A+90°
1
2
∠α=
变式3 如图,若换成两外角平分线相交于O,则∠BOC 与∠A 又有怎样的数量关系?
A
B
C
O
E
D
∵OB、OC分别是∠DBC、∠ECB的角平分线,
∴∠OBC =
∠DBC ,
1
2
∠OCB =
∠ECB ,
1
2
∵ ∠BOC = 180°-(∠OBC + ∠OCB)
∴ ∠BOC = 180°-( ∠DBC + ∠ECB)
= 180°- (∠DBC + ∠ECB)
= 180°- (∠A+∠ACB+∠ABC +∠A)
1
2
1
2
1
2
1
2
1
2
= 180°- (180°+∠A)
= 90°- ∠A
1
2
几何模型角平分线模型
α
O
B
C
A
90°- ∠A
1
2
∠α=
(2)两外角角平分线型
变式4 如图,若换成一内角与一外角平分线相交
于点O,则∠BOC与∠A 又有怎样的数量关系?
A
B
C
O
D
∵OB是∠ABC的角平分线,
∵OC是∠ACD的角平分线,
∴∠OBC =
∠ABC .
1
2
∴∠OCD =
∠ACD .
1
2
∵ ∠OCD = ∠OBC + ∠BOC,
∴ ∠BOC = ∠OCD - ∠OBC.
∵ ∠ACD = ∠ABC + ∠A,
∴ ∠BOC = (∠ABC + ∠A )
1
2
- ∠ABC
1
2
= ∠A.
1
2
几何模型之角平分线模型
(3)内外角角平分线型
α
A
B
C
O
D
∠A
1
2
∠α=
变式5 如图,若换成两条高相交于点O, ∠A 与∠BOC 又有怎样的数量关系?
A
B
C
O
E
D
∵BD、CE是△ ABC的高,
∴∠ ADB = ∠ AEC =90°.
∵∠A+∠AEC+∠EOD +∠ADO =360°,
∴ ∠A +∠EOD = 180°,
∴ ∠EOD = 180° - ∠A.
∵ ∠BOC = ∠EOD ,
∴ ∠EOD = 180° - ∠A.
1.列每组数分别表示三根木棒的长度,将它们首尾连结后,能摆成三角形的一组是( )
A.1,2,6 B.2,2,4
C.1,2,3 D.2,3,4
D
练习巩固
2.把一把直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为( )
A.120° B.125° C.130° D.140°
C
3.如图,一副分别含有30°和45°角的两个直角三角板,拼在一起,其中∠C=90°,∠B=45°, ∠E=30°,则∠BFD的度数是( )
A.10° B.25° C.30° D.15°
D
4.一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )
A.165° B.120° C.150° D.135°
A
5.如图,在△ABC中,AD是△ABC的角平分线,∠B=67°,∠C=33°,则∠CAD的度数为( )
A.40° B.45° C.50° D.55°
A
6.如图,∠1=100°,∠C=70°,则∠A的大小是( )
A.10° B.20° C.30° D.80°
第6题
C
7.若三角形的两边分别为3 和5 ,则第三边长m 的取值范围是 __________ .
<
<
m
8
2
8.如图,(1)若AD ⊥BC,垂足为D,则:∠_____ =∠_____ = 90°;
A
B
C
D
E
F
ADB
ADC
8.如图,(2)若∠BAE =∠CAE, AE 与BC 相交于点E,则:线段AE 是△ABC 的________;
角平分线
A
B
C
D
E
F
8.如图,(3)若AF =CF,BF 与 AC 相交于
点F,则:△ABC 的中线是 .
BF
A
B
C
D
E
F
9.如图,在△ABC 中,已知∠BAC =80°,∠ABC =60°.
(1)∠C = ;
(2)若AE 是△ABC 的
角平分线,则:
∠AEC = ;
(3)若BF 是△ABC 的高,与角平分线AE 相交于点O,则∠EOF = .
A
B
C
O
E
F
40°
100°
130°
10.如图,△ABC中,∠A=α,∠ABC
的平分线与∠ACD的平分线交与点A1,得∠A1 ,∠A1BC的平分线与∠A1CD的平分线交与点A2 ,得∠A2 ……,则∠A6与α的数量
关系是 .
A
B
C
A1
D
A2
∠A6=
1
64
∠α
今天作业
课本P29页第8、11、12 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
