11.2.2 直角三角形 课件(共27张PPT)
文档属性
| 名称 | 11.2.2 直角三角形 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
八上数学同步精品课件
人教版八年级上册
11.2.2 直角三角形
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.了解直角三角形两个锐角的关系.(重点)
2.掌握有两个角互余的三角形是直角三角形.(难点)
3.会运用直角三角形的性质和判定进行相关计算.(难点)
求出下列各图中x的值.
解:180°-40°-60°=80°; 180°-90°-55°=80°;
x+2x+90=180;
x=30
x+x+50=180;
x=65
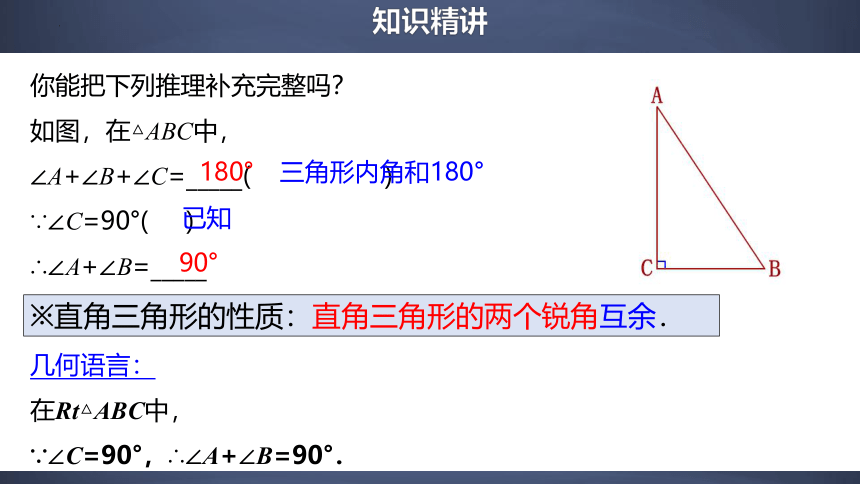
你能把下列推理补充完整吗?
如图,在△ABC中,
∠A+∠B+∠C=_____( )
∵∠C=90°( )
∴∠A+∠B=_____
180°
三角形内角和180°
已知
90°
※直角三角形的性质:直角三角形的两个锐角互余.
几何语言:
在Rt△ABC中,
∵∠C=90°,∴∠A+∠B=90°.
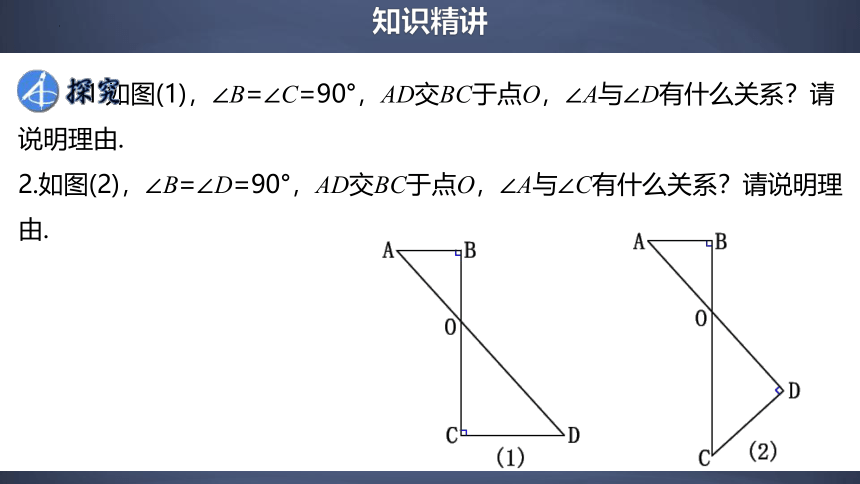
1.如图(1),∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?请说明理由.
2.如图(2),∠B=∠D=90°,AD交BC于点O,∠A与∠C有什么关系?请说明理由.
1.如图(1),∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?请说明理由.
方法一(利用平行的判定和性质):
∵∠B=∠C=90°,
∴AB∥CD,
∴∠A=∠D.
方法二(利用直角三角形的性质):
∵∠B=∠C=90°,
∴∠A+∠AOB=90°,∠D+∠COD=90°.
∵∠AOB=∠COD,
∴∠A=∠D.
∠A=∠D
2.如图(2),∠B=∠D=90°,AD交BC于点O,∠A与∠C有什么关系?请说明理由.
思考:
①两个图形的相同点和不同点各是什么?
②图(1)的两种解答方法能用于图(2)的解答吗?哪个更具一般性?
解:∠A=∠C.
理由如下:
在Rt△AOB和Rt△COD中,
∵∠B=∠D=90°
∴∠A+∠AOB=90°,∠C+∠COD=90°
∵∠AOB=∠COD
∴∠A=∠C
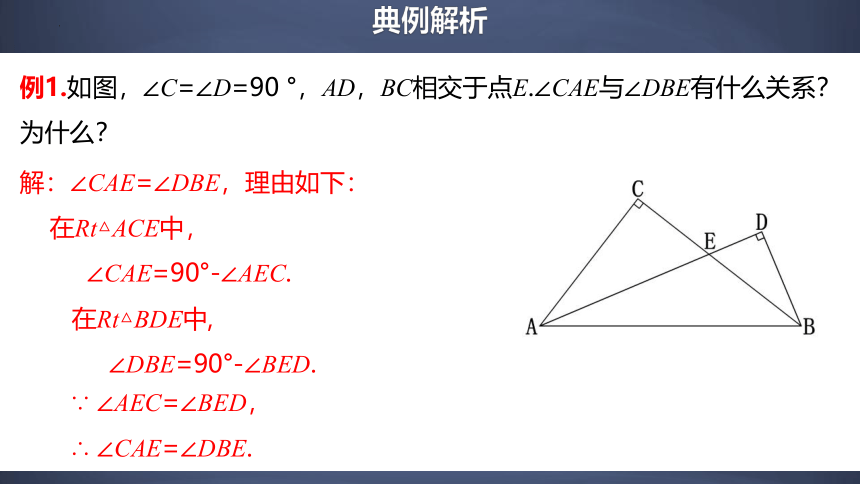
例1.如图,∠C=∠D=90 °,AD,BC相交于点E.∠CAE与∠DBE有什么关系?为什么?
解:∠CAE=∠DBE,理由如下:
在Rt△ACE中,
∠CAE=90°-∠AEC.
在Rt△BDE中,
∠DBE=90°-∠BED.
∵ ∠AEC=∠BED,
∴ ∠CAE=∠DBE.
如图,∠ACB=90°,CD⊥AB,垂足为D,∠ACD与∠B有什么关系?为什么?
解:∠ACD=∠B. 理由如下:
∵ ∠ACB=90°
∴ ∠ACD+∠BCD=90°
∵ CD⊥AB
∴ ∠BDC=90°
∴ ∠B+∠BCD=90°
∴ ∠ACD=∠B
我们知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,有两个角互余的三角形是直角三角形吗 请你说说理由.
问题:如图,在△ABC中,∠A+∠B=90°,那么△ABC是直角三角形吗?
解: △ABC是Rt△,理由如下:
在△ABC中,
∵∠A+∠B+∠C=180°, ∠A+∠B=90°,
∴∠C=180°-(∠A+∠B)=180°-90°=90°
∴△ABC是直角三角形.
※直角三角形的判定:有两个角互余的三角形是直角三角形.
几何语言:
在△ABC中,
∵∠A+∠B=90°,
∴△ABC是直角三角形.
例2.如图,CE⊥AD,垂足为E,∠A=∠C,△ABD是直角三角形吗?为什么?
解:△ABD是直角三角形.理由如下:
∵CE⊥AD,
∴∠CED=90°,
∴∠C+∠D=90°.
∵∠A=∠C,
∴∠A+∠D=90°,
∴△ABD是直角三角形.
如图,∠C=90 °, ∠1= ∠2,△ADE是直角三角形吗?为什么?
解:在Rt△ABC中, ∠2+∠A=90°.
∵ ∠1=∠2,
∴∠1+∠A=90°.
即△ADE是直角三角形.
例3.如图所示,有一个三角尺DEF(足够大),其中∠EDF=90°,把直角三角尺DEF放置在锐角△ABC上,三角尺DEF的两边DE,DF恰好分别经过点B,C.
(1)若∠A=35°,则∠ABC+∠ACB=_______°,∠DBC+∠DCB= ________°,∠ABD+∠ACD=_________°;
(2)若∠A=60°,求∠ABD+∠ACD的度数;
(3)请你猜想一下∠ABD+∠ACD与∠A所满足
的数量关系,并说明理由.
例3.如图所示,有一个三角尺DEF(足够大),其中∠EDF=90°,把直角三角尺DEF放置在锐角△ABC上,三角尺DEF的两边DE,DF恰好分别经过点B,C.
(1)若∠A=35°,则∠ABC+∠ACB=_______°,∠DBC+∠DCB= ________°,∠ABD+∠ACD=_________°;
解:∵∠A=35°,∠ABC+∠ACB+∠A=180°,
∴∠ABC+∠ACB=180°-∠A=145°;
∵∠BDC=90°,
∴∠DBC+∠DCB=90°,
∴∠ABD+∠ACD=∠ABC+∠ACB-∠DBC-∠DCB=55°
145
90
55
例3.如图所示,有一个三角尺DEF(足够大),其中∠EDF=90°,把直角三角尺DEF放置在锐角△ABC上,三角尺DEF的两边DE,DF恰好分别经过点B,C.
(2)若∠A=60°,求∠ABD+∠ACD的度数;
解:∵∠A=60°,∠ABC+∠ACB+∠A=180°,
∴∠ABC+∠ACB=180°-∠A=120°;
∵∠BDC=90°,
∴∠DBC+∠DCB=90°,
∴∠ABD+∠ACD=∠ABC+∠ACB-∠DBC-∠DCB=30°
例3.如图所示,有一个三角尺DEF(足够大),其中∠EDF=90°,把直角三角尺DEF放置在锐角△ABC上,三角尺DEF的两边DE,DF恰好分别经过点B,C.
(3)请你猜想一下∠ABD+∠ACD与∠A所满足的数量关系,并说明理由.
解:∠ABD+∠ACD+∠A=90°,理由如下:
∵∠ABC+∠ACB+∠A=180°,
∴∠ABC+∠ACB=180°-∠A;
∵∠BDC=90°,
∴∠DBC+∠DCB=90°,
∴∠ABD+∠ACD=∠ABC+∠ACB-∠DBC-∠DCB=180°-∠A-90°,
∴∠ABD+∠ACD+∠A=90°.
1.已知Rt△ABC的一个锐角为25°,则另一个锐角为______.
2.三角形的两个锐角分别为35°和55°,则它是_____三角形.
3.已知等腰三角形的顶角是底角的2倍,则这个三角形的顶角为_____,它是____________三角形.
4.如图,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC为______.
65°
直角
90°
等腰直角
80°
5.如图,∠1+∠2+∠3+∠4=______.
6.在三角形中,最大的内角不能小于_____,最小的内角不能大于_____.
7.如图,已知等腰三角ABC,底角的平分线BE与底边上的高AD相交与点O,且∠BOD=55°,则∠BAC=______.
280°
60°
60°
40°
8.如图,直线a//b,Rt△ABC如图放置,若∠1=28°,∠2=80°,则∠B的度数为( )
A.62° B.52° C.38° D.28°
C
9.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC, AD、BE相交于点F.
(1)若∠CAD=36°,求∠AEF的度数;
(2)试说明:∠AEF=∠AFE.
(1)解:∵AD⊥BC,
∴∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
∴∠ABD=∠CAD=36°,
∵BE平分∠ABC,
∴∠ABE=∠ABC=18°,
∴∠AEF=90°-∠ABE=72°.
9.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC, AD、BE相交于点F.
(1)若∠CAD=36°,求∠AEF的度数;
(2)试说明:∠AEF=∠AFE.
(2)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠ABE+∠AEF=90°,∠CBE+∠BFD=90°,
∴∠AEF=∠BFD,
∵∠AFE=∠BFD,
∴∠AEF=∠AFE.
※直角三角形的性质:直角三角形的两个锐角互余.
几何语言:
在Rt△ABC中,
∵∠C=90°,∴∠A+∠B=90°.
※直角三角形的判定:有两个角互余的三角形是直角三角形.
几何语言:
在△ABC中,
∵∠A+∠B=90°,
∴△ABC是直角三角形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
八上数学同步精品课件
人教版八年级上册
11.2.2 直角三角形
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.了解直角三角形两个锐角的关系.(重点)
2.掌握有两个角互余的三角形是直角三角形.(难点)
3.会运用直角三角形的性质和判定进行相关计算.(难点)
求出下列各图中x的值.
解:180°-40°-60°=80°; 180°-90°-55°=80°;
x+2x+90=180;
x=30
x+x+50=180;
x=65
你能把下列推理补充完整吗?
如图,在△ABC中,
∠A+∠B+∠C=_____( )
∵∠C=90°( )
∴∠A+∠B=_____
180°
三角形内角和180°
已知
90°
※直角三角形的性质:直角三角形的两个锐角互余.
几何语言:
在Rt△ABC中,
∵∠C=90°,∴∠A+∠B=90°.
1.如图(1),∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?请说明理由.
2.如图(2),∠B=∠D=90°,AD交BC于点O,∠A与∠C有什么关系?请说明理由.
1.如图(1),∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?请说明理由.
方法一(利用平行的判定和性质):
∵∠B=∠C=90°,
∴AB∥CD,
∴∠A=∠D.
方法二(利用直角三角形的性质):
∵∠B=∠C=90°,
∴∠A+∠AOB=90°,∠D+∠COD=90°.
∵∠AOB=∠COD,
∴∠A=∠D.
∠A=∠D
2.如图(2),∠B=∠D=90°,AD交BC于点O,∠A与∠C有什么关系?请说明理由.
思考:
①两个图形的相同点和不同点各是什么?
②图(1)的两种解答方法能用于图(2)的解答吗?哪个更具一般性?
解:∠A=∠C.
理由如下:
在Rt△AOB和Rt△COD中,
∵∠B=∠D=90°
∴∠A+∠AOB=90°,∠C+∠COD=90°
∵∠AOB=∠COD
∴∠A=∠C
例1.如图,∠C=∠D=90 °,AD,BC相交于点E.∠CAE与∠DBE有什么关系?为什么?
解:∠CAE=∠DBE,理由如下:
在Rt△ACE中,
∠CAE=90°-∠AEC.
在Rt△BDE中,
∠DBE=90°-∠BED.
∵ ∠AEC=∠BED,
∴ ∠CAE=∠DBE.
如图,∠ACB=90°,CD⊥AB,垂足为D,∠ACD与∠B有什么关系?为什么?
解:∠ACD=∠B. 理由如下:
∵ ∠ACB=90°
∴ ∠ACD+∠BCD=90°
∵ CD⊥AB
∴ ∠BDC=90°
∴ ∠B+∠BCD=90°
∴ ∠ACD=∠B
我们知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,有两个角互余的三角形是直角三角形吗 请你说说理由.
问题:如图,在△ABC中,∠A+∠B=90°,那么△ABC是直角三角形吗?
解: △ABC是Rt△,理由如下:
在△ABC中,
∵∠A+∠B+∠C=180°, ∠A+∠B=90°,
∴∠C=180°-(∠A+∠B)=180°-90°=90°
∴△ABC是直角三角形.
※直角三角形的判定:有两个角互余的三角形是直角三角形.
几何语言:
在△ABC中,
∵∠A+∠B=90°,
∴△ABC是直角三角形.
例2.如图,CE⊥AD,垂足为E,∠A=∠C,△ABD是直角三角形吗?为什么?
解:△ABD是直角三角形.理由如下:
∵CE⊥AD,
∴∠CED=90°,
∴∠C+∠D=90°.
∵∠A=∠C,
∴∠A+∠D=90°,
∴△ABD是直角三角形.
如图,∠C=90 °, ∠1= ∠2,△ADE是直角三角形吗?为什么?
解:在Rt△ABC中, ∠2+∠A=90°.
∵ ∠1=∠2,
∴∠1+∠A=90°.
即△ADE是直角三角形.
例3.如图所示,有一个三角尺DEF(足够大),其中∠EDF=90°,把直角三角尺DEF放置在锐角△ABC上,三角尺DEF的两边DE,DF恰好分别经过点B,C.
(1)若∠A=35°,则∠ABC+∠ACB=_______°,∠DBC+∠DCB= ________°,∠ABD+∠ACD=_________°;
(2)若∠A=60°,求∠ABD+∠ACD的度数;
(3)请你猜想一下∠ABD+∠ACD与∠A所满足
的数量关系,并说明理由.
例3.如图所示,有一个三角尺DEF(足够大),其中∠EDF=90°,把直角三角尺DEF放置在锐角△ABC上,三角尺DEF的两边DE,DF恰好分别经过点B,C.
(1)若∠A=35°,则∠ABC+∠ACB=_______°,∠DBC+∠DCB= ________°,∠ABD+∠ACD=_________°;
解:∵∠A=35°,∠ABC+∠ACB+∠A=180°,
∴∠ABC+∠ACB=180°-∠A=145°;
∵∠BDC=90°,
∴∠DBC+∠DCB=90°,
∴∠ABD+∠ACD=∠ABC+∠ACB-∠DBC-∠DCB=55°
145
90
55
例3.如图所示,有一个三角尺DEF(足够大),其中∠EDF=90°,把直角三角尺DEF放置在锐角△ABC上,三角尺DEF的两边DE,DF恰好分别经过点B,C.
(2)若∠A=60°,求∠ABD+∠ACD的度数;
解:∵∠A=60°,∠ABC+∠ACB+∠A=180°,
∴∠ABC+∠ACB=180°-∠A=120°;
∵∠BDC=90°,
∴∠DBC+∠DCB=90°,
∴∠ABD+∠ACD=∠ABC+∠ACB-∠DBC-∠DCB=30°
例3.如图所示,有一个三角尺DEF(足够大),其中∠EDF=90°,把直角三角尺DEF放置在锐角△ABC上,三角尺DEF的两边DE,DF恰好分别经过点B,C.
(3)请你猜想一下∠ABD+∠ACD与∠A所满足的数量关系,并说明理由.
解:∠ABD+∠ACD+∠A=90°,理由如下:
∵∠ABC+∠ACB+∠A=180°,
∴∠ABC+∠ACB=180°-∠A;
∵∠BDC=90°,
∴∠DBC+∠DCB=90°,
∴∠ABD+∠ACD=∠ABC+∠ACB-∠DBC-∠DCB=180°-∠A-90°,
∴∠ABD+∠ACD+∠A=90°.
1.已知Rt△ABC的一个锐角为25°,则另一个锐角为______.
2.三角形的两个锐角分别为35°和55°,则它是_____三角形.
3.已知等腰三角形的顶角是底角的2倍,则这个三角形的顶角为_____,它是____________三角形.
4.如图,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC为______.
65°
直角
90°
等腰直角
80°
5.如图,∠1+∠2+∠3+∠4=______.
6.在三角形中,最大的内角不能小于_____,最小的内角不能大于_____.
7.如图,已知等腰三角ABC,底角的平分线BE与底边上的高AD相交与点O,且∠BOD=55°,则∠BAC=______.
280°
60°
60°
40°
8.如图,直线a//b,Rt△ABC如图放置,若∠1=28°,∠2=80°,则∠B的度数为( )
A.62° B.52° C.38° D.28°
C
9.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC, AD、BE相交于点F.
(1)若∠CAD=36°,求∠AEF的度数;
(2)试说明:∠AEF=∠AFE.
(1)解:∵AD⊥BC,
∴∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
∴∠ABD=∠CAD=36°,
∵BE平分∠ABC,
∴∠ABE=∠ABC=18°,
∴∠AEF=90°-∠ABE=72°.
9.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC, AD、BE相交于点F.
(1)若∠CAD=36°,求∠AEF的度数;
(2)试说明:∠AEF=∠AFE.
(2)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠ABE+∠AEF=90°,∠CBE+∠BFD=90°,
∴∠AEF=∠BFD,
∵∠AFE=∠BFD,
∴∠AEF=∠AFE.
※直角三角形的性质:直角三角形的两个锐角互余.
几何语言:
在Rt△ABC中,
∵∠C=90°,∴∠A+∠B=90°.
※直角三角形的判定:有两个角互余的三角形是直角三角形.
几何语言:
在△ABC中,
∵∠A+∠B=90°,
∴△ABC是直角三角形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
