11.2.3 三角形的外角 课件(共32张PPT)
文档属性
| 名称 | 11.2.3 三角形的外角 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 09:30:48 | ||
图片预览





文档简介
(共32张PPT)
八上数学同步精品课件
人教版八年级上册
11.2.3 三角形的外角
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.理解并掌握三角形的外角的概念,并能够在复杂图形中找出外角.
2.掌握三角形的外角的性质和三角形外角和.(重点)
3.会利用三角形的外角性质解决有关问题.(难点)
C
D
三角形的内角是三角形内部的骄子.
那三角形的外部呢?
什么都没有呀,让人感到很无奈!
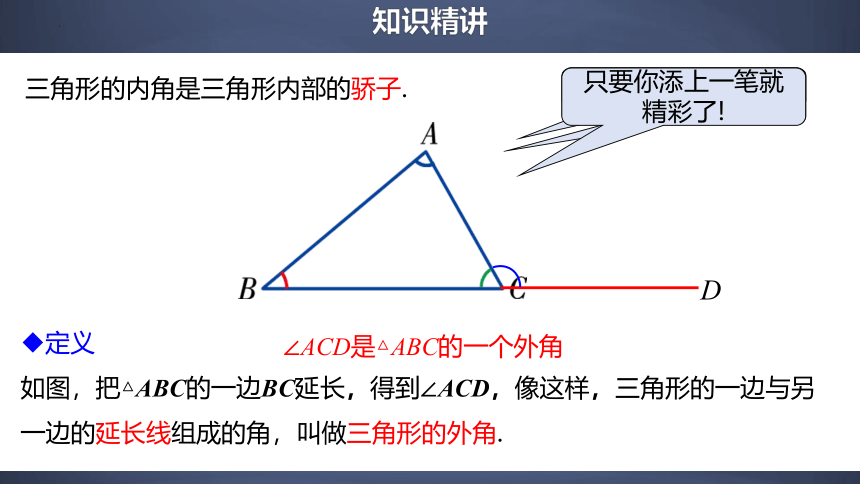
只要你添上一笔就精彩了!
D
定义
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
∠ACD是△ABC的一个外角
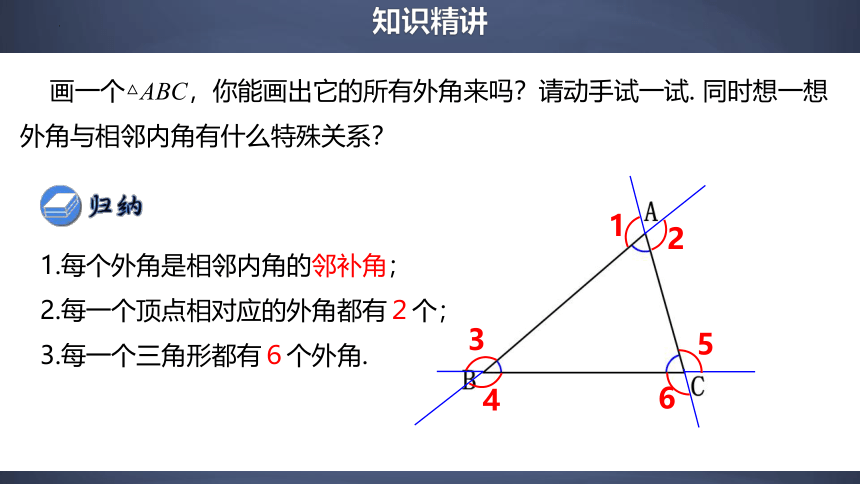
画一个△ABC,你能画出它的所有外角来吗?请动手试一试. 同时想一想外角与相邻内角有什么特殊关系?
1
2
3
4
5
6
1.每个外角是相邻内角的邻补角;
2.每一个顶点相对应的外角都有2个;
3.每一个三角形都有6个外角.
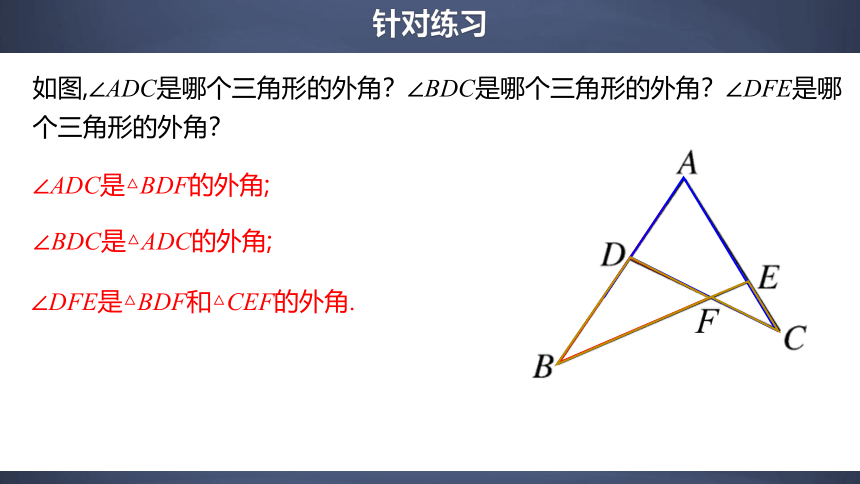
如图,∠ADC是哪个三角形的外角?∠BDC是哪个三角形的外角?∠DFE是哪个三角形的外角?
∠ADC是△BDF的外角;
∠BDC是△ADC的外角;
∠DFE是△BDF和△CEF的外角.
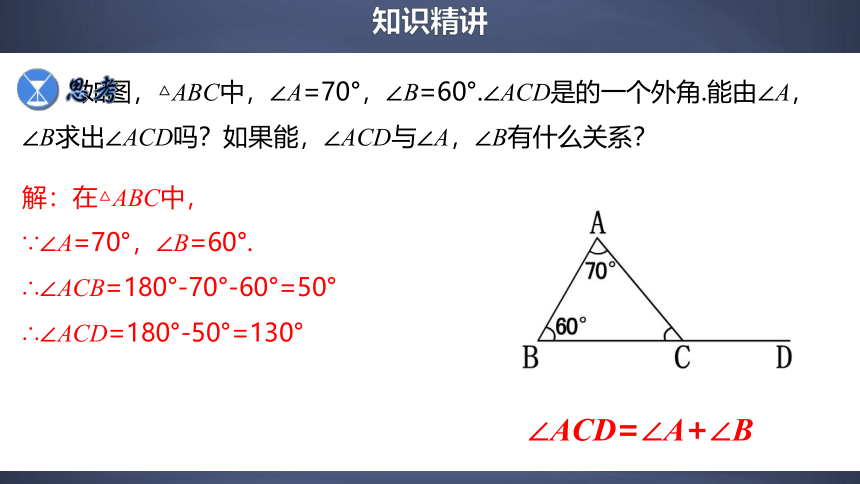
如图,△ABC中,∠A=70°,∠B=60°.∠ACD是的一个外角.能由∠A,∠B求出∠ACD吗?如果能,∠ACD与∠A,∠B有什么关系?
解:在△ABC中,
∵∠A=70°,∠B=60°.
∴∠ACB=180°-70°-60°=50°
∴∠ACD=180°-50°=130°
∠ACD=∠A+∠B
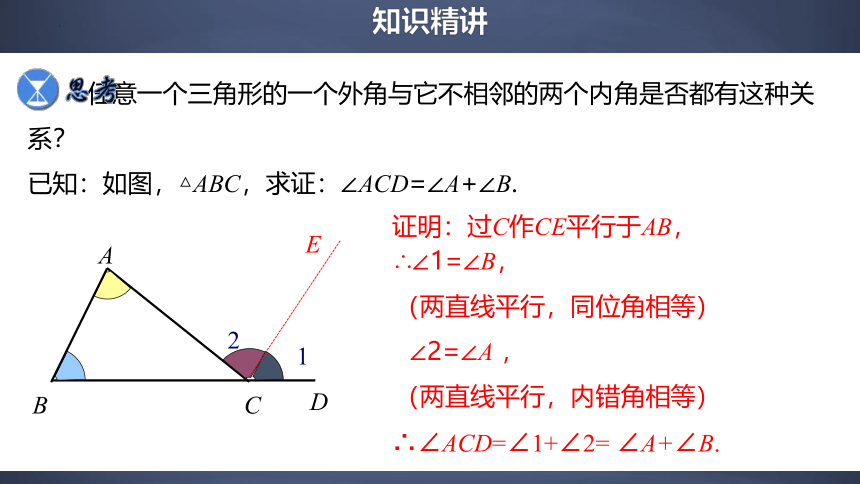
任意一个三角形的一个外角与它不相邻的两个内角是否都有这种关系?
D
证明:过C作CE平行于AB,
A
B
C
1
2
∴∠1=∠B,
(两直线平行,同位角相等)
∠2=∠A ,
(两直线平行,内错角相等)
∴∠ACD=∠1+∠2= ∠A+∠B.
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
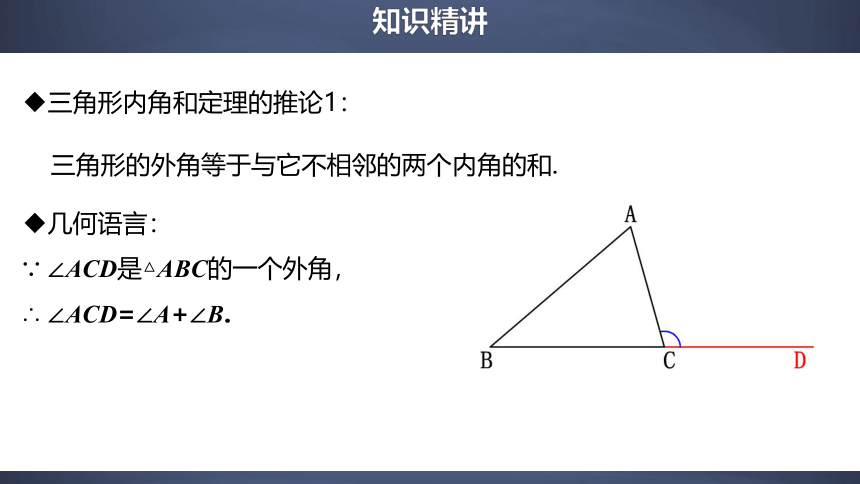
三角形内角和定理的推论1:
三角形的外角等于与它不相邻的两个内角的和.
几何语言:
∵ ∠ACD是△ABC的一个外角,
∴ ∠ACD=∠A+∠B.
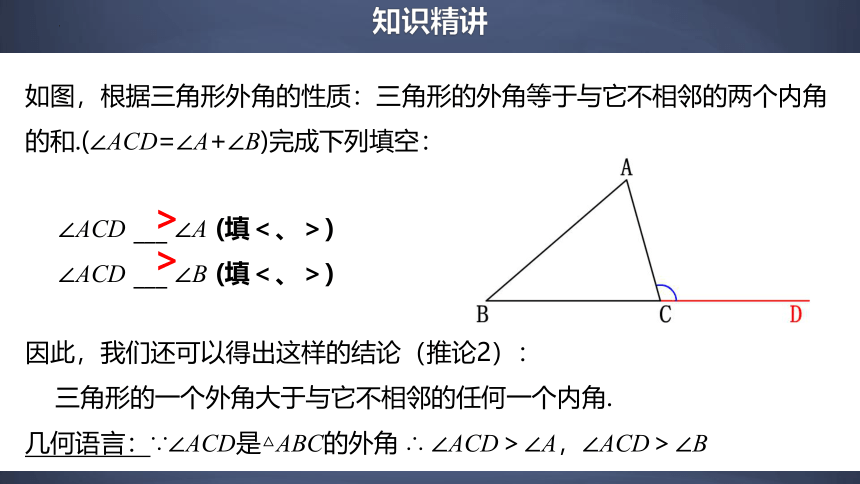
如图,根据三角形外角的性质:三角形的外角等于与它不相邻的两个内角的和.(∠ACD=∠A+∠B)完成下列填空:
∠ACD ___ ∠A (填<、>)
∠ACD ___ ∠B (填<、>)
>
>
因此,我们还可以得出这样的结论(推论2):
三角形的一个外角大于与它不相邻的任何一个内角.
几何语言:∵∠ACD是△ABC的外角 ∴ ∠ACD>∠A,∠ACD>∠B
C
D
例1.如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,它们的和是多少?
解:由三角形的一个外角等于与它不相邻的两个
内角和,得
∠BAE=∠2+∠3,
∠CBF=∠1+∠3,
∠ACD=∠1+∠2
所以 ∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3) ,
由∠1+∠2+∠3=180°,得∠BAE+∠CBF+∠ACD=2×180°=360°.
你还有其它解法吗?
解法二:如图,∠BAE+∠1=180° ① ,
∠CBF+∠2=180° ②,
∠ACD+∠3=180° ③,
又知∠1+∠2+∠3=180°,
①+②+③得
∠BAE+∠CBF+∠ACD+(∠1+∠2+∠3)=540 °,
所以∠BAE+∠CBF+∠ACD=540°-180°=360°.
结论:三角形的外角和等于360°.
说出下列图形中∠1和∠2的度数.
例2.如图,在△ABC中,∠BAC=80°,∠B=60°,AD是△ABC的高,点E在BC边上,且AE是∠DAC的角平分线,EF//AC,求∠AEC和∠AFE的度数.
解:∵AD是△ABC的高,
∴∠ADB=∠ADC=90°,
∴∠B+∠BAD=90°,
∵∠B=60°,
∴∠BAD=30°,
∵∠BAC=80°,
∴∠DAC=∠BAC-∠BAD=50°,
又∵AE是∠DAC的角平分线,
∴∠DAE=∠DAC=25°,
∵∠AEC是△ADE的外角,
例2.如图,在△ABC中,∠BAC=80°,∠B=60°,AD是△ABC的高,点E在BC边上,且AE是∠DAC的角平分线,EF//AC,求∠AEC和∠AFE的度数.
∴∠AEC=∠ADC+∠DAE=90°+25°=115°,
∵∠BAC=80°,∠B=60°,
∠BAC+∠B+∠C=180°,
∴∠C=40°,
∵EF∥AC,
∴∠DEF=∠C=40°,
∵∠AFE是△DEF的外角,
∴∠AFE=∠ADC+∠DEF=90°+40°=130°.
如图,点O是△ABC内一点,连接BO,CO,CO恰好平分∠ACB,延长BO交AC于点E.已知∠A=50°,∠BCO=35°,∠BEC=65°,求∠ABO和∠OBC的度数.
解:∵∠A=50°,∠BCO=35°,
∴∠ABO=∠BEC-∠A=65°-50°=15°,
∵CO平分∠ACB ,∠BCO=35°,
∴∠BCA=2∠BCO=70°,
∴∠ABO=180°-∠A-∠BCA=180°-50°-70°=60°,
∴∠OBC=∠ABC-∠ABO= 60°-15°=45°.
例3.如图,已知AD是△ABD和△ACD的公共边.求证:∠BDC=∠BAC+∠B
+∠C.
证明:延长AD.
∵∠BDE与∠CDE分别是△ABD与△ACD
的外角,
∴∠BDE=∠1+∠B,∠CDE=∠2+∠C,
∵∠BAC=∠1+∠2,∠BDC=∠BDE+∠CDE,
∴∠BDC=∠1+∠B+∠2+∠C
=∠BAC+∠B+∠C.
如图,∠A=51°,∠B=20°,∠C=30°,求∠BDC的度数.
A
B
C
D
(
(
(
51 °
20 °
30 °
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
解法一:连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51°+20°+30°=101°.
E
你发现了什么结论?
A
B
C
D
(
(
(
51 °
20 °
30 °
E
)
1
解法二:延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC
=∠BAC+∠ABD+∠ACD
=51°+20°+30°=101°.
解法三:连接延长CD交AB于点F(解题过程同解法二).
)
2
F
【点睛】解题的关键是正确的构造三角形,利用三角形外角的性质及转化的思想,把未知角与已知角联系起来求解.
你发现了什么结论?
A
B
C
D
(
(
(
※基本几何图形---飞镖形
数量关系:∠BDC=∠BAC+∠ABD+∠ACD
1.三角形的三个内角之比分别是1:2:3,则此三角形的最大外角为______度.
2.三角形的三个外角(各顶点取一个)中,最多有____个锐角;
3.等腰三角形的一个外角为150°,则它的底角为_____________.
4.如图,∠1=_____.
150
1
30°或75°
120°
5.如图,CE⊥AF于E,若∠F=40°,∠C=50°,则∠DBC=_____.
6.如图,AB//CD,∠A=38°,∠C=80°,则∠M=_____.
80°
42°
7.求出图中的x的值.
解:由三角形的一个外角等于与它不相邻的两个内角的和,列方程得
x+x+10=x+70,
解得x=60,
因此,x的值为60.
8.如图,在五角星的图中,求∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个外角,
∴∠1=∠B+∠D,
∵∠2是△EHC的一个外角,
∴∠2=∠C+∠E,
∵∠A+∠1+∠2=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
9.已知:如图,在△ABC中,AD平分外角∠EAC,∠B=∠C.求证: AD//BC.
证明:∵∠EAC=∠B+∠C且∠B=∠C,
∴∠B=∠EAC,
∵AD平分∠EAC,
∴∠DAE=∠EAC,
∴∠DAE=∠B,
∴AD//BC.
10.如图,BD是∠ABC的角平分线,CD是△ABC的外角平分线,BD、CD交于D,试探索∠A与∠D的关系.
解:∵∠ACE是△ABC的外角,∴∠ACE=∠A+∠ABC,
∵BD平分∠ABC,CD平分∠ACE, ∴∠DBC=∠ABC,∠DCE=∠ACE,
∴∠DCE= ∠A+∠DBC,
∵∠DCE是△DBC的外角,∴∠DCE=∠D+∠DBC,
∴∠D+∠DBC=∠A+∠DBC,
即∠D=∠A.
定义
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
三角形内角和定理的推论1:
三角形的外角等于与它不相邻的两个内角的和.
几何语言:
∵ ∠ACD是△ABC的一个外角,∴ ∠ACD=∠A+∠B.
三角形的一个外角大于与它不相邻的任何一个内角.
几何语言:∵∠ACD是△ABC的外角 ∴ ∠ACD>∠A,∠ACD>∠B
三角形内角和定理的推论2:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
八上数学同步精品课件
人教版八年级上册
11.2.3 三角形的外角
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.理解并掌握三角形的外角的概念,并能够在复杂图形中找出外角.
2.掌握三角形的外角的性质和三角形外角和.(重点)
3.会利用三角形的外角性质解决有关问题.(难点)
C
D
三角形的内角是三角形内部的骄子.
那三角形的外部呢?
什么都没有呀,让人感到很无奈!
只要你添上一笔就精彩了!
D
定义
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
∠ACD是△ABC的一个外角
画一个△ABC,你能画出它的所有外角来吗?请动手试一试. 同时想一想外角与相邻内角有什么特殊关系?
1
2
3
4
5
6
1.每个外角是相邻内角的邻补角;
2.每一个顶点相对应的外角都有2个;
3.每一个三角形都有6个外角.
如图,∠ADC是哪个三角形的外角?∠BDC是哪个三角形的外角?∠DFE是哪个三角形的外角?
∠ADC是△BDF的外角;
∠BDC是△ADC的外角;
∠DFE是△BDF和△CEF的外角.
如图,△ABC中,∠A=70°,∠B=60°.∠ACD是的一个外角.能由∠A,∠B求出∠ACD吗?如果能,∠ACD与∠A,∠B有什么关系?
解:在△ABC中,
∵∠A=70°,∠B=60°.
∴∠ACB=180°-70°-60°=50°
∴∠ACD=180°-50°=130°
∠ACD=∠A+∠B
任意一个三角形的一个外角与它不相邻的两个内角是否都有这种关系?
D
证明:过C作CE平行于AB,
A
B
C
1
2
∴∠1=∠B,
(两直线平行,同位角相等)
∠2=∠A ,
(两直线平行,内错角相等)
∴∠ACD=∠1+∠2= ∠A+∠B.
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
三角形内角和定理的推论1:
三角形的外角等于与它不相邻的两个内角的和.
几何语言:
∵ ∠ACD是△ABC的一个外角,
∴ ∠ACD=∠A+∠B.
如图,根据三角形外角的性质:三角形的外角等于与它不相邻的两个内角的和.(∠ACD=∠A+∠B)完成下列填空:
∠ACD ___ ∠A (填<、>)
∠ACD ___ ∠B (填<、>)
>
>
因此,我们还可以得出这样的结论(推论2):
三角形的一个外角大于与它不相邻的任何一个内角.
几何语言:∵∠ACD是△ABC的外角 ∴ ∠ACD>∠A,∠ACD>∠B
C
D
例1.如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,它们的和是多少?
解:由三角形的一个外角等于与它不相邻的两个
内角和,得
∠BAE=∠2+∠3,
∠CBF=∠1+∠3,
∠ACD=∠1+∠2
所以 ∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3) ,
由∠1+∠2+∠3=180°,得∠BAE+∠CBF+∠ACD=2×180°=360°.
你还有其它解法吗?
解法二:如图,∠BAE+∠1=180° ① ,
∠CBF+∠2=180° ②,
∠ACD+∠3=180° ③,
又知∠1+∠2+∠3=180°,
①+②+③得
∠BAE+∠CBF+∠ACD+(∠1+∠2+∠3)=540 °,
所以∠BAE+∠CBF+∠ACD=540°-180°=360°.
结论:三角形的外角和等于360°.
说出下列图形中∠1和∠2的度数.
例2.如图,在△ABC中,∠BAC=80°,∠B=60°,AD是△ABC的高,点E在BC边上,且AE是∠DAC的角平分线,EF//AC,求∠AEC和∠AFE的度数.
解:∵AD是△ABC的高,
∴∠ADB=∠ADC=90°,
∴∠B+∠BAD=90°,
∵∠B=60°,
∴∠BAD=30°,
∵∠BAC=80°,
∴∠DAC=∠BAC-∠BAD=50°,
又∵AE是∠DAC的角平分线,
∴∠DAE=∠DAC=25°,
∵∠AEC是△ADE的外角,
例2.如图,在△ABC中,∠BAC=80°,∠B=60°,AD是△ABC的高,点E在BC边上,且AE是∠DAC的角平分线,EF//AC,求∠AEC和∠AFE的度数.
∴∠AEC=∠ADC+∠DAE=90°+25°=115°,
∵∠BAC=80°,∠B=60°,
∠BAC+∠B+∠C=180°,
∴∠C=40°,
∵EF∥AC,
∴∠DEF=∠C=40°,
∵∠AFE是△DEF的外角,
∴∠AFE=∠ADC+∠DEF=90°+40°=130°.
如图,点O是△ABC内一点,连接BO,CO,CO恰好平分∠ACB,延长BO交AC于点E.已知∠A=50°,∠BCO=35°,∠BEC=65°,求∠ABO和∠OBC的度数.
解:∵∠A=50°,∠BCO=35°,
∴∠ABO=∠BEC-∠A=65°-50°=15°,
∵CO平分∠ACB ,∠BCO=35°,
∴∠BCA=2∠BCO=70°,
∴∠ABO=180°-∠A-∠BCA=180°-50°-70°=60°,
∴∠OBC=∠ABC-∠ABO= 60°-15°=45°.
例3.如图,已知AD是△ABD和△ACD的公共边.求证:∠BDC=∠BAC+∠B
+∠C.
证明:延长AD.
∵∠BDE与∠CDE分别是△ABD与△ACD
的外角,
∴∠BDE=∠1+∠B,∠CDE=∠2+∠C,
∵∠BAC=∠1+∠2,∠BDC=∠BDE+∠CDE,
∴∠BDC=∠1+∠B+∠2+∠C
=∠BAC+∠B+∠C.
如图,∠A=51°,∠B=20°,∠C=30°,求∠BDC的度数.
A
B
C
D
(
(
(
51 °
20 °
30 °
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
解法一:连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51°+20°+30°=101°.
E
你发现了什么结论?
A
B
C
D
(
(
(
51 °
20 °
30 °
E
)
1
解法二:延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC
=∠BAC+∠ABD+∠ACD
=51°+20°+30°=101°.
解法三:连接延长CD交AB于点F(解题过程同解法二).
)
2
F
【点睛】解题的关键是正确的构造三角形,利用三角形外角的性质及转化的思想,把未知角与已知角联系起来求解.
你发现了什么结论?
A
B
C
D
(
(
(
※基本几何图形---飞镖形
数量关系:∠BDC=∠BAC+∠ABD+∠ACD
1.三角形的三个内角之比分别是1:2:3,则此三角形的最大外角为______度.
2.三角形的三个外角(各顶点取一个)中,最多有____个锐角;
3.等腰三角形的一个外角为150°,则它的底角为_____________.
4.如图,∠1=_____.
150
1
30°或75°
120°
5.如图,CE⊥AF于E,若∠F=40°,∠C=50°,则∠DBC=_____.
6.如图,AB//CD,∠A=38°,∠C=80°,则∠M=_____.
80°
42°
7.求出图中的x的值.
解:由三角形的一个外角等于与它不相邻的两个内角的和,列方程得
x+x+10=x+70,
解得x=60,
因此,x的值为60.
8.如图,在五角星的图中,求∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个外角,
∴∠1=∠B+∠D,
∵∠2是△EHC的一个外角,
∴∠2=∠C+∠E,
∵∠A+∠1+∠2=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
9.已知:如图,在△ABC中,AD平分外角∠EAC,∠B=∠C.求证: AD//BC.
证明:∵∠EAC=∠B+∠C且∠B=∠C,
∴∠B=∠EAC,
∵AD平分∠EAC,
∴∠DAE=∠EAC,
∴∠DAE=∠B,
∴AD//BC.
10.如图,BD是∠ABC的角平分线,CD是△ABC的外角平分线,BD、CD交于D,试探索∠A与∠D的关系.
解:∵∠ACE是△ABC的外角,∴∠ACE=∠A+∠ABC,
∵BD平分∠ABC,CD平分∠ACE, ∴∠DBC=∠ABC,∠DCE=∠ACE,
∴∠DCE= ∠A+∠DBC,
∵∠DCE是△DBC的外角,∴∠DCE=∠D+∠DBC,
∴∠D+∠DBC=∠A+∠DBC,
即∠D=∠A.
定义
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
三角形内角和定理的推论1:
三角形的外角等于与它不相邻的两个内角的和.
几何语言:
∵ ∠ACD是△ABC的一个外角,∴ ∠ACD=∠A+∠B.
三角形的一个外角大于与它不相邻的任何一个内角.
几何语言:∵∠ACD是△ABC的外角 ∴ ∠ACD>∠A,∠ACD>∠B
三角形内角和定理的推论2:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
