11.3.1 多边形的有关概念 课件(共29张PPT)
文档属性
| 名称 | 11.3.1 多边形的有关概念 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
八上数学同步精品课件
人教版八年级上册
11.3.1多边形的有关概念
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.掌握多边形的定义及有关概念,能区分凹凸多边形.
2.掌握正多边形的概念.(重点)
3.会求多边形的对角线的条数.(难点)
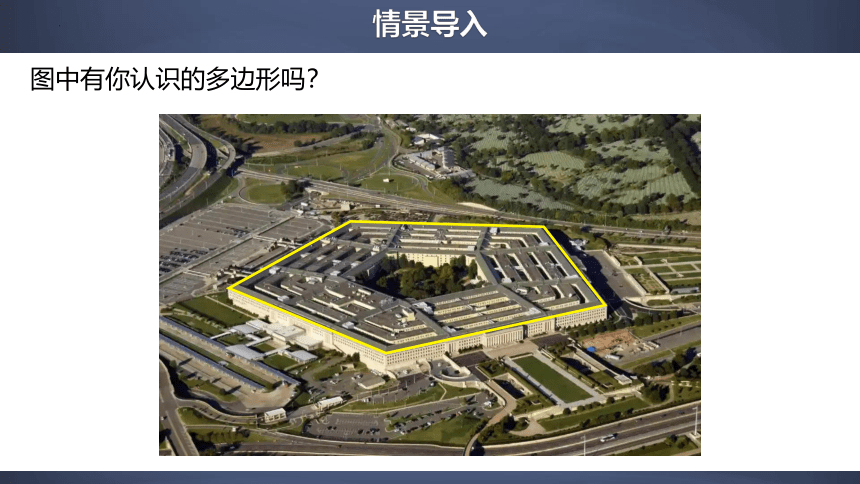
图中有你认识的多边形吗?
从这些图形中,你能抽象出哪些平面图形?
三角形
长方形
四边形
五边形
六边形
八边形
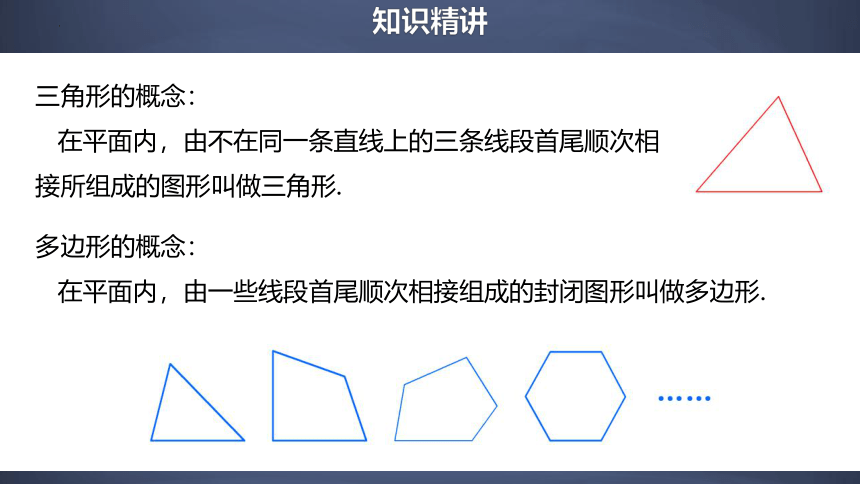
三角形的概念:
在平面内,由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
多边形的概念:
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
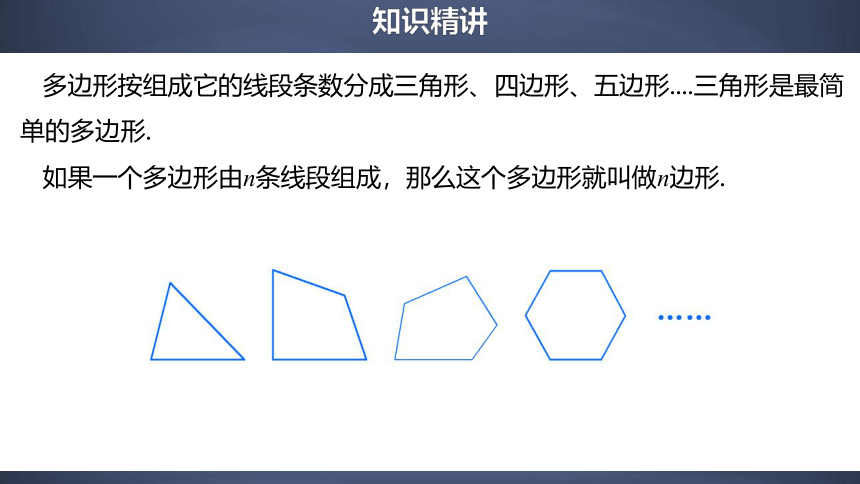
多边形按组成它的线段条数分成三角形、四边形、五边形....三角形是最简单的多边形.
如果一个多边形由n条线段组成,那么这个多边形就叫做n边形.
★多边形的内角:
多边形相邻两边组成的角叫做它的内角.图中∠A,∠B,∠C,∠D,∠E是五边形ABCDE的5个内角.
内角:多边形相邻两边组成的角
顶点
边
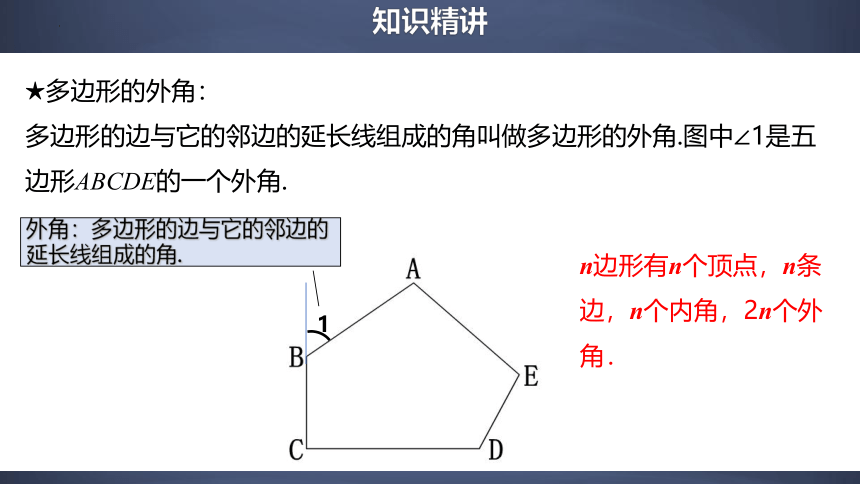
★多边形的外角:
多边形的边与它的邻边的延长线组成的角叫做多边形的外角.图中∠1是五边形ABCDE的一个外角.
外角:多边形的边与它的邻边的延长线组成的角.
1
n边形有n个顶点,n条边,n个内角,2n个外角.
★多边形的对角线:
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线. 图中,AC,AD是五边形ABCDE的两条对角线.
对角线:连接多边形不相邻的两个顶点的线段.
思考:五边形ABCDE共有几条对角线?请画出它的其他对角线.
★多边形的组成元素:
多边形的顶点、边、内角、外角、对角线是组成多边形的关键元素.
如图所示,五边形ABCDE,则点B是它的一个_____, CD是它的一条___,∠E是它的一个______,∠FAE是它的一个______,AD是它的一条________.
顶点
边
内角
外角
对角线
下列两个多边形有何异同呢?
凸多边形的判断方法:
画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形. 反之,则是凹多边形. 本节只讨论凸多边形.
下列图形中,哪些是凸多边形
凸多边形
凸多边形
观察下列多边形,它们的边、角各有什么特点?
像正方形一样,各个角都相等,各条边都相等的多边形叫正多边形.
正三角形
正方形
正五边形
正六边形
判断下列说法是否正确.若不正确,举一个反例说明.
(1)所有角都相等的多边形是正多边形;
(2)所有边都相等的多边形是正多边形.
解:(1)错误,如长方形:
(2)错误,如菱形:
n-3
n-2
0
1
1
0
2
2
2
3
5
3
4
9
4
5
14
从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.将多边形分成(n-2)个三角形.
n(n≥3)边形共有对角线 条.
例1.如图所示,是一个正方形的纸片,如果纸片剪下一个角后,问纸片还剩几个角 剩下的纸片是几边形 它共有几条对角线
解:剪下一个角后,剩余的纸片有三种情形:
(1)有5个角,是五边形,共有5条对角线;
(2)有3个角,是三角形,没有对角线;
(3)有4个角,是四边形,共有2条对角线.
【点睛】一个n边形截去一个角后,n边形的边数可能为n条、(n-1)条、 (n+1)条.
例2.已知:从n边形的一个顶点出发共有4条对角线;从m边形的一个顶点出发的所有对角线把m边形分成6个三角形;正t边形的边长为7,周长为63.求 的值.
解:依题意有n=4+3=7,
m=6+2=8,
t=63÷7=9,
则(n﹣m)t=(7﹣8)9=﹣1.
【点睛】从n边形的一个顶点出发,能引出(n﹣3)条对角线,一共有条对角线,经过多边形的一个顶点的所有对角线把多边形分成(n﹣2)个三角形.
1.若一个多边形从一个顶点可以引5条对角线,则它是( )
A.五边形 B.六边形 C.七边形 D.八边形
2.过多边形的一个顶点的对角线把多边形分成8个三角形,那么这个多边形的边数为( )
A.8 B.9 C.10 D.11
3.一个多边形有14条对角线,那么这个多边形的边数是( )
A.5 B.6 C.7 D.8
D
C
C
4.一个多边形截去一个角后,变成16边形,那么原来的多边形的边数为( )
A.15或16或17 B.15或17 C.16或17 D.16或17或18
A
5.把一个多边形纸片沿一条直线截下一个三角形后,变成一个十八边形,则原多边形纸片的边数可能是_______________________________.
十七边形或十八边形或十九边形
6.从六边形的一个顶点出发,可以画出m条对角线,它们将六边形分成n个三角形.k边形没有对角线,则m+n+k的值为______.
10
7.如图,要把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小正三角形的边长是多少?
解:小正三角形和正六边形的各边都分别相等,且每个小正三角形与正六边形均有公共边,
∴AD=DK=KB,
又∵AD+DK+KB=12,
∴3AD=12,
∴AD=4,
即剪去的小正三角形的边长是4.
8.已知从n边形的一个顶点出发共有4条对角线,该n边形的周长为56,且各边长是连续的自然数,求这个多边形的各边长.
解:由n-3=4得n=7,
设边长为x-3,x-2,x-1,x,x+1,x+2,x+3,
则7x=56,
解得x=8.
各边之长为5,6,7,8,9,10,11.
★多边形的组成元素:
多边形的顶点、边、内角、外角、对角线是组成多边形的关键元素.
※重要结论:
1.从n边形的一个顶点出发,能引出(n﹣3)条对角线;
2.经过n边形的一个顶点的所有对角线把多边形分成(n﹣2)个三角形;
3. n边形一共有条对角线.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
八上数学同步精品课件
人教版八年级上册
11.3.1多边形的有关概念
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.掌握多边形的定义及有关概念,能区分凹凸多边形.
2.掌握正多边形的概念.(重点)
3.会求多边形的对角线的条数.(难点)
图中有你认识的多边形吗?
从这些图形中,你能抽象出哪些平面图形?
三角形
长方形
四边形
五边形
六边形
八边形
三角形的概念:
在平面内,由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
多边形的概念:
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
多边形按组成它的线段条数分成三角形、四边形、五边形....三角形是最简单的多边形.
如果一个多边形由n条线段组成,那么这个多边形就叫做n边形.
★多边形的内角:
多边形相邻两边组成的角叫做它的内角.图中∠A,∠B,∠C,∠D,∠E是五边形ABCDE的5个内角.
内角:多边形相邻两边组成的角
顶点
边
★多边形的外角:
多边形的边与它的邻边的延长线组成的角叫做多边形的外角.图中∠1是五边形ABCDE的一个外角.
外角:多边形的边与它的邻边的延长线组成的角.
1
n边形有n个顶点,n条边,n个内角,2n个外角.
★多边形的对角线:
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线. 图中,AC,AD是五边形ABCDE的两条对角线.
对角线:连接多边形不相邻的两个顶点的线段.
思考:五边形ABCDE共有几条对角线?请画出它的其他对角线.
★多边形的组成元素:
多边形的顶点、边、内角、外角、对角线是组成多边形的关键元素.
如图所示,五边形ABCDE,则点B是它的一个_____, CD是它的一条___,∠E是它的一个______,∠FAE是它的一个______,AD是它的一条________.
顶点
边
内角
外角
对角线
下列两个多边形有何异同呢?
凸多边形的判断方法:
画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形. 反之,则是凹多边形. 本节只讨论凸多边形.
下列图形中,哪些是凸多边形
凸多边形
凸多边形
观察下列多边形,它们的边、角各有什么特点?
像正方形一样,各个角都相等,各条边都相等的多边形叫正多边形.
正三角形
正方形
正五边形
正六边形
判断下列说法是否正确.若不正确,举一个反例说明.
(1)所有角都相等的多边形是正多边形;
(2)所有边都相等的多边形是正多边形.
解:(1)错误,如长方形:
(2)错误,如菱形:
n-3
n-2
0
1
1
0
2
2
2
3
5
3
4
9
4
5
14
从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.将多边形分成(n-2)个三角形.
n(n≥3)边形共有对角线 条.
例1.如图所示,是一个正方形的纸片,如果纸片剪下一个角后,问纸片还剩几个角 剩下的纸片是几边形 它共有几条对角线
解:剪下一个角后,剩余的纸片有三种情形:
(1)有5个角,是五边形,共有5条对角线;
(2)有3个角,是三角形,没有对角线;
(3)有4个角,是四边形,共有2条对角线.
【点睛】一个n边形截去一个角后,n边形的边数可能为n条、(n-1)条、 (n+1)条.
例2.已知:从n边形的一个顶点出发共有4条对角线;从m边形的一个顶点出发的所有对角线把m边形分成6个三角形;正t边形的边长为7,周长为63.求 的值.
解:依题意有n=4+3=7,
m=6+2=8,
t=63÷7=9,
则(n﹣m)t=(7﹣8)9=﹣1.
【点睛】从n边形的一个顶点出发,能引出(n﹣3)条对角线,一共有条对角线,经过多边形的一个顶点的所有对角线把多边形分成(n﹣2)个三角形.
1.若一个多边形从一个顶点可以引5条对角线,则它是( )
A.五边形 B.六边形 C.七边形 D.八边形
2.过多边形的一个顶点的对角线把多边形分成8个三角形,那么这个多边形的边数为( )
A.8 B.9 C.10 D.11
3.一个多边形有14条对角线,那么这个多边形的边数是( )
A.5 B.6 C.7 D.8
D
C
C
4.一个多边形截去一个角后,变成16边形,那么原来的多边形的边数为( )
A.15或16或17 B.15或17 C.16或17 D.16或17或18
A
5.把一个多边形纸片沿一条直线截下一个三角形后,变成一个十八边形,则原多边形纸片的边数可能是_______________________________.
十七边形或十八边形或十九边形
6.从六边形的一个顶点出发,可以画出m条对角线,它们将六边形分成n个三角形.k边形没有对角线,则m+n+k的值为______.
10
7.如图,要把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小正三角形的边长是多少?
解:小正三角形和正六边形的各边都分别相等,且每个小正三角形与正六边形均有公共边,
∴AD=DK=KB,
又∵AD+DK+KB=12,
∴3AD=12,
∴AD=4,
即剪去的小正三角形的边长是4.
8.已知从n边形的一个顶点出发共有4条对角线,该n边形的周长为56,且各边长是连续的自然数,求这个多边形的各边长.
解:由n-3=4得n=7,
设边长为x-3,x-2,x-1,x,x+1,x+2,x+3,
则7x=56,
解得x=8.
各边之长为5,6,7,8,9,10,11.
★多边形的组成元素:
多边形的顶点、边、内角、外角、对角线是组成多边形的关键元素.
※重要结论:
1.从n边形的一个顶点出发,能引出(n﹣3)条对角线;
2.经过n边形的一个顶点的所有对角线把多边形分成(n﹣2)个三角形;
3. n边形一共有条对角线.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
