11.3.2 多边形的内角和 课件(共36张PPT)
文档属性
| 名称 | 11.3.2 多边形的内角和 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 10:17:40 | ||
图片预览





文档简介
(共36张PPT)
八上数学同步精品课件
人教版八年级上册
11.3.2 多边形的内角和
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.能通过不同方法探索多边形的内角和与外角和公式.(重点)
2.学会运用多边形的内角和与外角和公式解决问题.(难点)
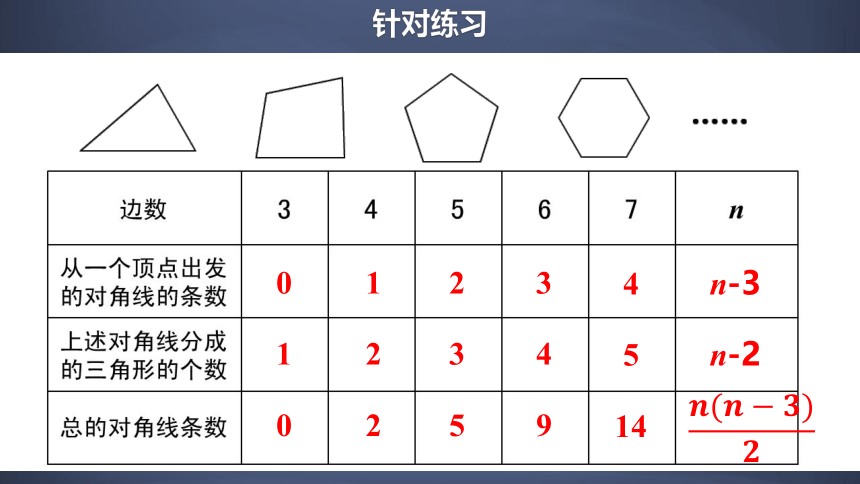
n-3
n-2
0
1
1
0
2
2
2
3
5
3
4
9
4
5
14
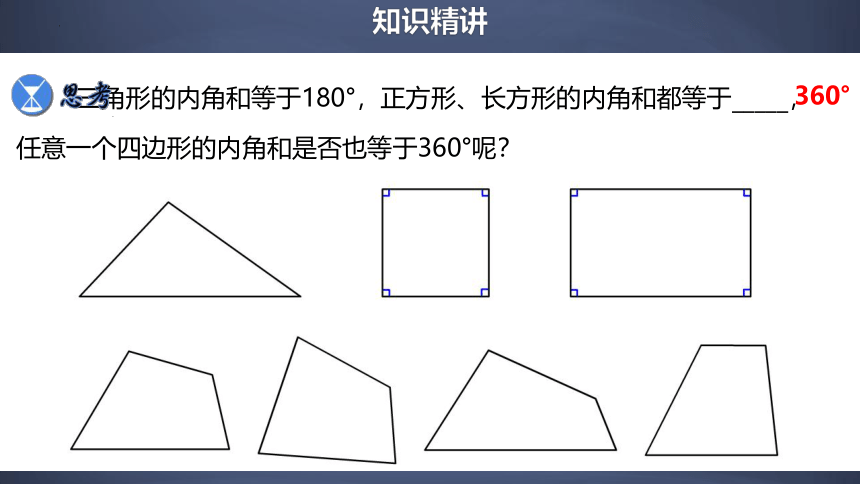
三角形的内角和等于180°,正方形、长方形的内角和都等于_____,
任意一个四边形的内角和是否也等于360°呢?
360°
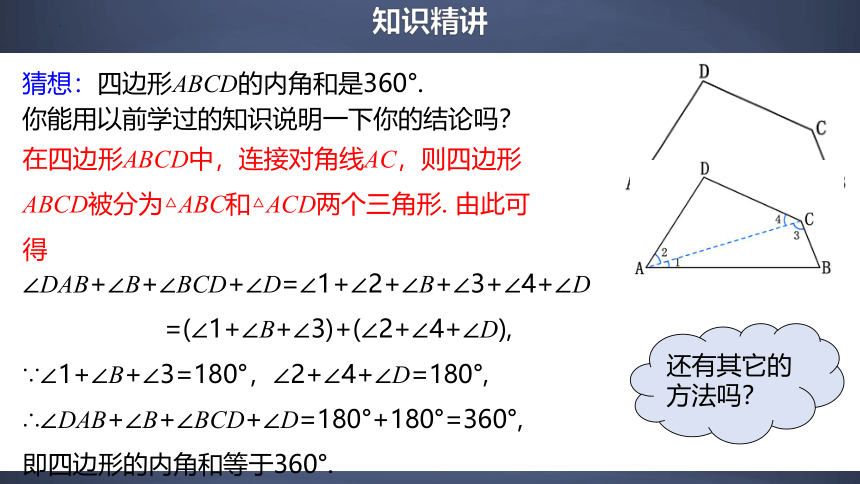
在四边形ABCD中,连接对角线AC,则四边形ABCD被分为△ABC和△ACD两个三角形. 由此可得
猜想:四边形ABCD的内角和是360°.
你能用以前学过的知识说明一下你的结论吗?
∠DAB+∠B+∠BCD+∠D=∠1+∠2+∠B+∠3+∠4+∠D
=(∠1+∠B+∠3)+(∠2+∠4+∠D),
∵∠1+∠B+∠3=180°,∠2+∠4+∠D=180°,
∴∠DAB+∠B+∠BCD+∠D=180°+180°=360°,
即四边形的内角和等于360°.
还有其它的方法吗?
E
证法2:如图,在AB边上任取一点E,连接CE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3-(∠AED+∠BEC+∠CED)=180°×3-180°=360°.
E
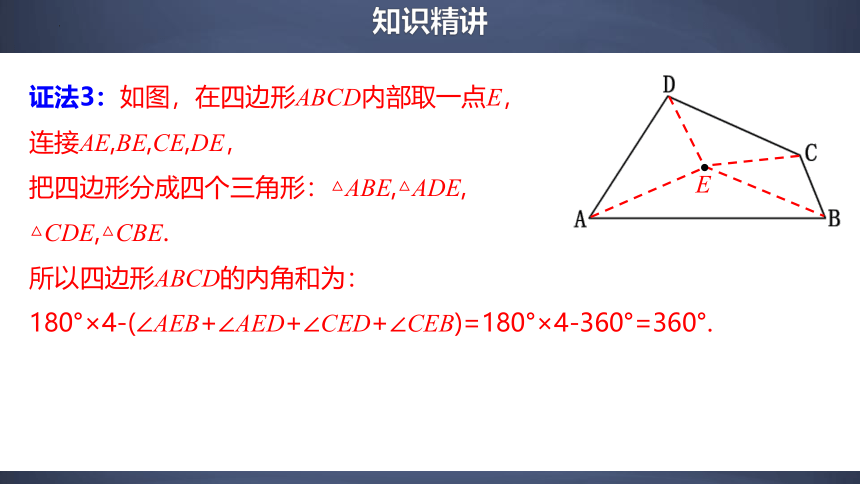
证法3:如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,
把四边形分成四个三角形:△ABE,△ADE,
△CDE,△CBE.
所以四边形ABCD的内角和为:
180°×4-(∠AEB+∠AED+∠CED+∠CEB)=180°×4-360°=360°.
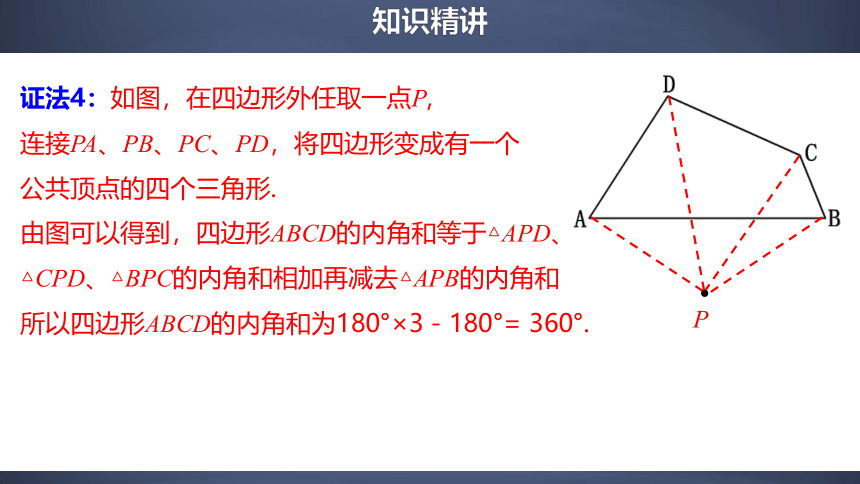
P
证法4:如图,在四边形外任取一点P,
连接PA、PB、PC、PD,将四边形变成有一个公共顶点的四个三角形.
由图可以得到,四边形ABCD的内角和等于△APD、
△CPD、△BPC的内角和相加再减去△APB的内角和
所以四边形ABCD的内角和为180°×3-180°= 360°.
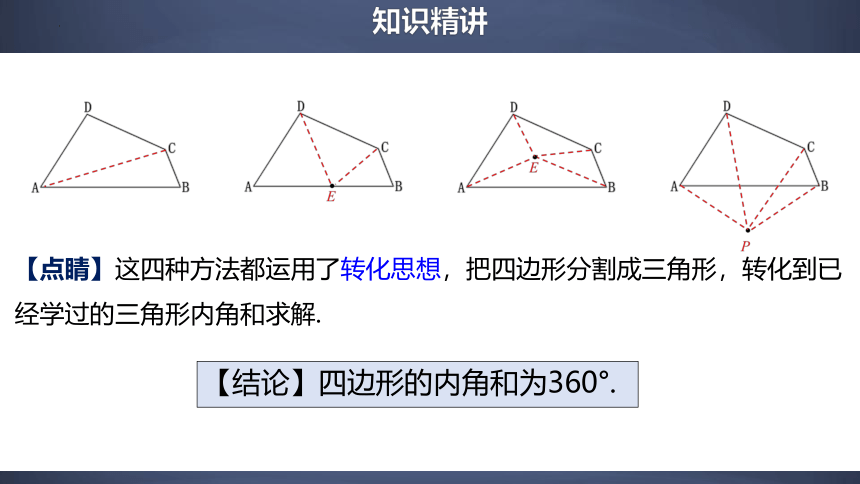
【点睛】这四种方法都运用了转化思想,把四边形分割成三角形,转化到已经学过的三角形内角和求解.
【结论】四边形的内角和为360°.
2
3
180°×3=540°
3
4
180°×4=720°
n-3
n-2
180°×(n-2)
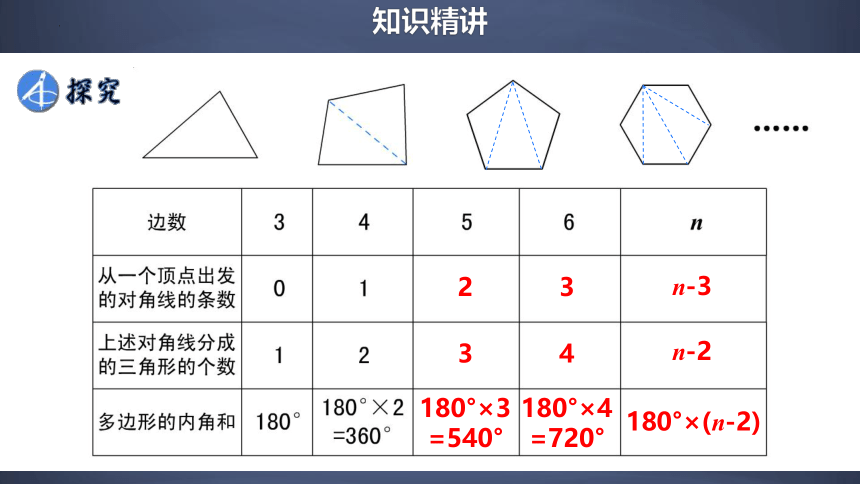
一般地,从n边形的一个顶点出发,可以作(n-3)条对角线,它们将n边形分为(n-2)个三角形,n边形的内角和等于180°×(n-2).
这样就得出了多边形内角和公式:n边形的内角和等于(n-2)×180°.
【尝试验证】
用把一个多边形分成几个三角形的其他分法来验证是否能得出多边形的内角和公式?
例1.如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:如图,四边形ABCD中,∠A+∠C=180°.
∵∠A+∠B+∠C+∠D=(4-2)×180°=360 °,
∴∠B+∠D=360°-(∠A+∠C)
=360°-180°
=180°.
如果一个四边形的一组对角互补,那么另一组对角互补.
求下列图形中x的值:
解:(1) x+x+140+90=360,解得 x=65.
(2) 90+120+150+2x+x=(5-2)×180,解得 x=60.
(3) 75+120+80+(180-x)=360,解得 x=95.
例2.如图,在六边形的每一个顶点处各取一个外角,这些外角的和叫做六边形的外角和. 六边形的外角和等于多少?
【分析】考虑以下问题:
(1)任何一个外角同与它相邻的内角有什么关系
(2)六边形的6个外角加上与它们相邻的内角所得总和是多少
(3)上述总和与六边形的内角和、外角和有什么关系
例2.如图,在六边形的每一个顶点处各取一个外角,这些外角的和叫做六边形的外角和. 六边形的外角和等于多少?
解:六边形的任何一个外角加上与它相邻的内角都等于180°,
因此六边形的6个外角加上与它们相邻的内角,所得总和等于6×180°,
这个总和就是六边形的外角和加上内角和,
所以外角和等于总和减去内角和,即外角和等于
6×180°-(6-2)×180°=2×180°=360°.
例2中,六边形的外角和=6×180°-(6-2)×180°=2×180°=360°
如果将例2中的六边形换为n边形(n是不小于3的任意整数),可以得到同样的结果吗?
n边形的外角和=n×180°-(n-2)×180°
=n×180°-n×180°+2×180°
=2×180°
=360°
【结论】 n边形的外角和等于360°.
如图,从多边形的一个顶点A出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发时的方向. 在行程中所转的各个角的和,就是多边形的外角和. 由于走了一周,所转的各个角的和等于一个周角,所以多边形的外角和等于360°.
回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
练一练:
(1)若一个正多边形的内角是120 °,那么这是正____边形.
(2)已知多边形的每个外角都是45°,则这个多边形是 ______边形.
六
正八
例3.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于 (n-2) 180°,
外角和等于360°,
∴ (n-2) 180°=2×360°.
解得 n=6.
∴这个多边形的边数为6.
1.一个多边形的各内角都等于120°,它是几边形?
2.一个多边形的各内角和与外角和相等,它是几边形?
解法一:∵ 各内角都等于120°,
∴ 每个外角都是60°,
∴ 边数为:360°÷60°=6,
即它是六边形.
解:设它是n边形,依题意得,
(n-2)×180=360,
解得,n=4,
即它是四边形.
解法二:设它是n边形.
120n=(n-2)×180,
解得,n=6,
即它是六边形.
例4.一个多边形除了一个内角之外,其余内角之和为2670°,求这个多边形的边数和少加的内角的大小.
解:设多边形的边数为x,由题意有
(x﹣2) 180=2670,
解得x=16,
因而多边形的边数是17,
则这一内角为(17﹣2)×180°-2670°=30°.
答:这个多边形的边数是17,少加的内角是30°.
如图是两位小朋友在探究某多边形的内角和时的一段对话,请根据他们的对话内容判断他们是在求几边形?少加的内角为多少度?
解:1140°÷180°=6…60°,
则边数是:6+1+2=9;
他们在求九边形的内角和;
180°﹣60°=120°,
少加的那个内角为120度.
例5.一个多边形剪去一个内角后,得到一个内角和为1980°的新多边形,求原多边形的边数.
解:设新的多边形的边数为n,
∵新的多边形的内角和是1980°,
∴180°×(n﹣2)=1980°,
解得:n=13,
∵一个多边形从某一个顶点出发截去一个角后所形成的新的多边形是十三边形,
①若截去一个角后边数增加1,则原多边形边数为12,
②若截去一个角后边数不变,则原多边形边数为13,
③若截去一个角后边数减少1,则原多边形边数为14,
∴原多边形的边数可能是:12或13或14.
已知在一个多边形中,除去一个内角外,其余内角和的度数是1125°,求这个多边形的边数.
解:设这个多边形的边数为x,这个内角为α,根据题意,
得(x-2) 180°=1125°+ α,
α =(x-2) 180°-1125°
由0<α<180°,
解得:8.25<x<9.25.
则该多边形边数是9.
1.一个多边形的内角和等于720°,这个多边形的边数为______;
2.一个多边形的每个内角都等于140°,那么这个多边形是_____边形;
3.如果一个多边形的边数增加1,那么这个多边形的内角和增加______度;
4.若一个多边形的各边都相等,它的周长是63,且它的内角和为900°,则它的边长是_______;
5.若一个十边形的每个外角都相等,则它的每个外角的度数为_____,内角和为__________.
6
九
180
9
36°
1440°
6.若一个n边形的内角都相等,且内角的度数与和它相邻的外角的度数比为3:1,那么,这个多边形的边数为_____;
7.一个多边形的内角和等于它的外角和的4倍,那么这个多边形是____边形;
8.小华从A点出发向前直走50m后,向左转18°,继续向前走50m,再左转18°,他以同样走法回到A点时,共走_______m;
9.如果一个多边形的每一个外角都相等,并且它的内角和为2880°,那么它的内角为_______.
8
十
1000
160
10.当一个多边形的边数增加时,其外角和( )
A.增加 B.减少 C.不变 D.不能确定
11.某学生在计算四个多边形的内角和时,得到下列四个答案,其中错误的是( )
A.180 B.540 C.1080 D.1900
C
D
12.一个多边形截去一个角(不过顶点)后,形成的多边形的内角和是2520°,那么原多边形的边数是( )
A.13 B.14 C.15 D.13或15
13.一个多边形的外角中,钝角的个数不可能是( )
A.1个 B.2个 C.3个 D.4个
14.不能作为正多边形的内角的度数的是( )
A.120 B.130 C.135° D.144
C
D
B
15.一个多边形的内角和比它的外角和的3倍少180°,这个多边形的边数是多少?
解:设这个多边形的边数为n,
根据题意,得(n-2)×180°=3×360°-180°,
解得n=7.
答:这个多边形的边数为7.
16.如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
解:连接BE,构造出四边形ABEF.
∵∠1=∠C+∠D,∠1=∠CBE+∠DEB,
∴∠C+∠D=∠CBE+∠DEB,
∴∠A+∠ABC+∠C+D+∠DEF+∠F
=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F
=360°.
17.有一张长方形的木板面,现在锯掉它的一个角,剩下残余木板面所有的内角和是多少
解:①(3-2)×180°=180°
②(4-2)×180°=360°
③(5-2)×180°=540°
分割
多边形
三角形
分割点与多边形的位置关系
顶点
边上
内部
外部
转化思想
1.n边形的内角和公式:n边形的内角和等于(n-2)×180 °.
2.n边形的外角和360°.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
八上数学同步精品课件
人教版八年级上册
11.3.2 多边形的内角和
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.能通过不同方法探索多边形的内角和与外角和公式.(重点)
2.学会运用多边形的内角和与外角和公式解决问题.(难点)
n-3
n-2
0
1
1
0
2
2
2
3
5
3
4
9
4
5
14
三角形的内角和等于180°,正方形、长方形的内角和都等于_____,
任意一个四边形的内角和是否也等于360°呢?
360°
在四边形ABCD中,连接对角线AC,则四边形ABCD被分为△ABC和△ACD两个三角形. 由此可得
猜想:四边形ABCD的内角和是360°.
你能用以前学过的知识说明一下你的结论吗?
∠DAB+∠B+∠BCD+∠D=∠1+∠2+∠B+∠3+∠4+∠D
=(∠1+∠B+∠3)+(∠2+∠4+∠D),
∵∠1+∠B+∠3=180°,∠2+∠4+∠D=180°,
∴∠DAB+∠B+∠BCD+∠D=180°+180°=360°,
即四边形的内角和等于360°.
还有其它的方法吗?
E
证法2:如图,在AB边上任取一点E,连接CE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3-(∠AED+∠BEC+∠CED)=180°×3-180°=360°.
E
证法3:如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,
把四边形分成四个三角形:△ABE,△ADE,
△CDE,△CBE.
所以四边形ABCD的内角和为:
180°×4-(∠AEB+∠AED+∠CED+∠CEB)=180°×4-360°=360°.
P
证法4:如图,在四边形外任取一点P,
连接PA、PB、PC、PD,将四边形变成有一个公共顶点的四个三角形.
由图可以得到,四边形ABCD的内角和等于△APD、
△CPD、△BPC的内角和相加再减去△APB的内角和
所以四边形ABCD的内角和为180°×3-180°= 360°.
【点睛】这四种方法都运用了转化思想,把四边形分割成三角形,转化到已经学过的三角形内角和求解.
【结论】四边形的内角和为360°.
2
3
180°×3=540°
3
4
180°×4=720°
n-3
n-2
180°×(n-2)
一般地,从n边形的一个顶点出发,可以作(n-3)条对角线,它们将n边形分为(n-2)个三角形,n边形的内角和等于180°×(n-2).
这样就得出了多边形内角和公式:n边形的内角和等于(n-2)×180°.
【尝试验证】
用把一个多边形分成几个三角形的其他分法来验证是否能得出多边形的内角和公式?
例1.如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:如图,四边形ABCD中,∠A+∠C=180°.
∵∠A+∠B+∠C+∠D=(4-2)×180°=360 °,
∴∠B+∠D=360°-(∠A+∠C)
=360°-180°
=180°.
如果一个四边形的一组对角互补,那么另一组对角互补.
求下列图形中x的值:
解:(1) x+x+140+90=360,解得 x=65.
(2) 90+120+150+2x+x=(5-2)×180,解得 x=60.
(3) 75+120+80+(180-x)=360,解得 x=95.
例2.如图,在六边形的每一个顶点处各取一个外角,这些外角的和叫做六边形的外角和. 六边形的外角和等于多少?
【分析】考虑以下问题:
(1)任何一个外角同与它相邻的内角有什么关系
(2)六边形的6个外角加上与它们相邻的内角所得总和是多少
(3)上述总和与六边形的内角和、外角和有什么关系
例2.如图,在六边形的每一个顶点处各取一个外角,这些外角的和叫做六边形的外角和. 六边形的外角和等于多少?
解:六边形的任何一个外角加上与它相邻的内角都等于180°,
因此六边形的6个外角加上与它们相邻的内角,所得总和等于6×180°,
这个总和就是六边形的外角和加上内角和,
所以外角和等于总和减去内角和,即外角和等于
6×180°-(6-2)×180°=2×180°=360°.
例2中,六边形的外角和=6×180°-(6-2)×180°=2×180°=360°
如果将例2中的六边形换为n边形(n是不小于3的任意整数),可以得到同样的结果吗?
n边形的外角和=n×180°-(n-2)×180°
=n×180°-n×180°+2×180°
=2×180°
=360°
【结论】 n边形的外角和等于360°.
如图,从多边形的一个顶点A出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发时的方向. 在行程中所转的各个角的和,就是多边形的外角和. 由于走了一周,所转的各个角的和等于一个周角,所以多边形的外角和等于360°.
回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
练一练:
(1)若一个正多边形的内角是120 °,那么这是正____边形.
(2)已知多边形的每个外角都是45°,则这个多边形是 ______边形.
六
正八
例3.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于 (n-2) 180°,
外角和等于360°,
∴ (n-2) 180°=2×360°.
解得 n=6.
∴这个多边形的边数为6.
1.一个多边形的各内角都等于120°,它是几边形?
2.一个多边形的各内角和与外角和相等,它是几边形?
解法一:∵ 各内角都等于120°,
∴ 每个外角都是60°,
∴ 边数为:360°÷60°=6,
即它是六边形.
解:设它是n边形,依题意得,
(n-2)×180=360,
解得,n=4,
即它是四边形.
解法二:设它是n边形.
120n=(n-2)×180,
解得,n=6,
即它是六边形.
例4.一个多边形除了一个内角之外,其余内角之和为2670°,求这个多边形的边数和少加的内角的大小.
解:设多边形的边数为x,由题意有
(x﹣2) 180=2670,
解得x=16,
因而多边形的边数是17,
则这一内角为(17﹣2)×180°-2670°=30°.
答:这个多边形的边数是17,少加的内角是30°.
如图是两位小朋友在探究某多边形的内角和时的一段对话,请根据他们的对话内容判断他们是在求几边形?少加的内角为多少度?
解:1140°÷180°=6…60°,
则边数是:6+1+2=9;
他们在求九边形的内角和;
180°﹣60°=120°,
少加的那个内角为120度.
例5.一个多边形剪去一个内角后,得到一个内角和为1980°的新多边形,求原多边形的边数.
解:设新的多边形的边数为n,
∵新的多边形的内角和是1980°,
∴180°×(n﹣2)=1980°,
解得:n=13,
∵一个多边形从某一个顶点出发截去一个角后所形成的新的多边形是十三边形,
①若截去一个角后边数增加1,则原多边形边数为12,
②若截去一个角后边数不变,则原多边形边数为13,
③若截去一个角后边数减少1,则原多边形边数为14,
∴原多边形的边数可能是:12或13或14.
已知在一个多边形中,除去一个内角外,其余内角和的度数是1125°,求这个多边形的边数.
解:设这个多边形的边数为x,这个内角为α,根据题意,
得(x-2) 180°=1125°+ α,
α =(x-2) 180°-1125°
由0<α<180°,
解得:8.25<x<9.25.
则该多边形边数是9.
1.一个多边形的内角和等于720°,这个多边形的边数为______;
2.一个多边形的每个内角都等于140°,那么这个多边形是_____边形;
3.如果一个多边形的边数增加1,那么这个多边形的内角和增加______度;
4.若一个多边形的各边都相等,它的周长是63,且它的内角和为900°,则它的边长是_______;
5.若一个十边形的每个外角都相等,则它的每个外角的度数为_____,内角和为__________.
6
九
180
9
36°
1440°
6.若一个n边形的内角都相等,且内角的度数与和它相邻的外角的度数比为3:1,那么,这个多边形的边数为_____;
7.一个多边形的内角和等于它的外角和的4倍,那么这个多边形是____边形;
8.小华从A点出发向前直走50m后,向左转18°,继续向前走50m,再左转18°,他以同样走法回到A点时,共走_______m;
9.如果一个多边形的每一个外角都相等,并且它的内角和为2880°,那么它的内角为_______.
8
十
1000
160
10.当一个多边形的边数增加时,其外角和( )
A.增加 B.减少 C.不变 D.不能确定
11.某学生在计算四个多边形的内角和时,得到下列四个答案,其中错误的是( )
A.180 B.540 C.1080 D.1900
C
D
12.一个多边形截去一个角(不过顶点)后,形成的多边形的内角和是2520°,那么原多边形的边数是( )
A.13 B.14 C.15 D.13或15
13.一个多边形的外角中,钝角的个数不可能是( )
A.1个 B.2个 C.3个 D.4个
14.不能作为正多边形的内角的度数的是( )
A.120 B.130 C.135° D.144
C
D
B
15.一个多边形的内角和比它的外角和的3倍少180°,这个多边形的边数是多少?
解:设这个多边形的边数为n,
根据题意,得(n-2)×180°=3×360°-180°,
解得n=7.
答:这个多边形的边数为7.
16.如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
解:连接BE,构造出四边形ABEF.
∵∠1=∠C+∠D,∠1=∠CBE+∠DEB,
∴∠C+∠D=∠CBE+∠DEB,
∴∠A+∠ABC+∠C+D+∠DEF+∠F
=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F
=360°.
17.有一张长方形的木板面,现在锯掉它的一个角,剩下残余木板面所有的内角和是多少
解:①(3-2)×180°=180°
②(4-2)×180°=360°
③(5-2)×180°=540°
分割
多边形
三角形
分割点与多边形的位置关系
顶点
边上
内部
外部
转化思想
1.n边形的内角和公式:n边形的内角和等于(n-2)×180 °.
2.n边形的外角和360°.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
