数学人教A版2019选择性必修第一册2.4.1圆的标准方程 课件(共27张ppt)
文档属性
| 名称 | 数学人教A版2019选择性必修第一册2.4.1圆的标准方程 课件(共27张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 10:57:57 | ||
图片预览






文档简介
(共27张PPT)
2.4圆的方程
直线与圆的方程
2.4.1圆的标准方程
课程标准
回顾确定圆的几何要素,在平面直角坐标系中,探索与掌握圆的标准方程
新课导入
多边形和圆是平面几何中的两类基本图形.
建立直线的方程后,我们可以运用它研究多边形这些“直线形”,解决边所在直线的平行或垂直、边与边的交点以及点到线段所在直线的距离等问题.
类似地,为了研究圆的有关性质,解决与圆有关的问题,我们首先需要建立圆的方程.
一
二
三
教学目标
掌握圆的定义及其标准方程
会根据圆的标准方程,掌握圆的标准方程的特征
会用待定系数法求圆的标准方程,判断点与圆的位置关系
教学目标
难点
重点
新知探究
探究一:圆的标准方程
新知讲解
问题1 在平面直角坐标系中,如何确定一个圆呢?
换句话说:圆的定义是什么?
类似于直线方程的建立过程,为建立圆的方程,我们首先考虑确定一个圆的几何要素.
圆是平面上到定点的距离等于定长的点的集合.
新知讲解
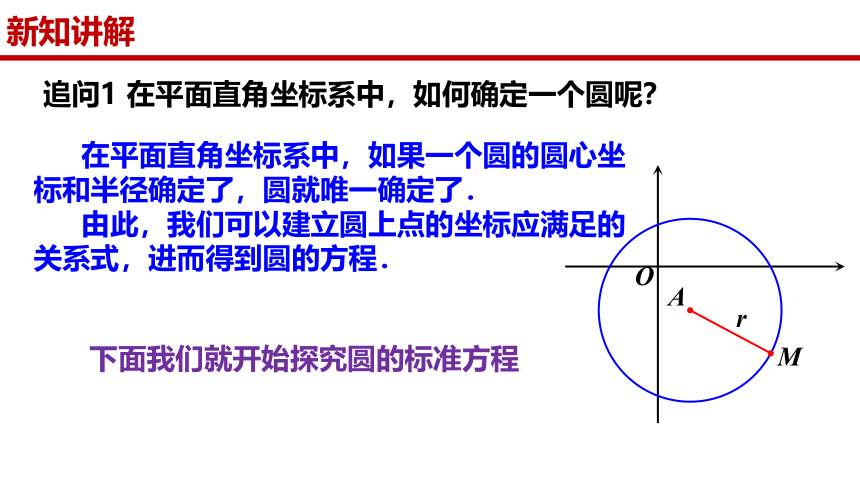
追问1 在平面直角坐标系中,如何确定一个圆呢?
在平面直角坐标系中,如果一个圆的圆心坐标和半径确定了,圆就唯一确定了.
由此,我们可以建立圆上点的坐标应满足的关系式,进而得到圆的方程.
A
M
r
O
下面我们就开始探究圆的标准方程
新知讲解
问题2 圆的标准方程是什么?
建:建立直角坐标系
假设:点M的坐标为
如图,在平面直角坐标系中,A 的圆心A的坐标为,半径为,为圆上任意一点,A就是以下点的集合.
设:用坐标表示有关的量
限:限制条件
代:进行有关代数运算
化:化简
根据两点间的距离公式
点M的坐标满足的条件可以表示为,
两边平方,得
概念生成
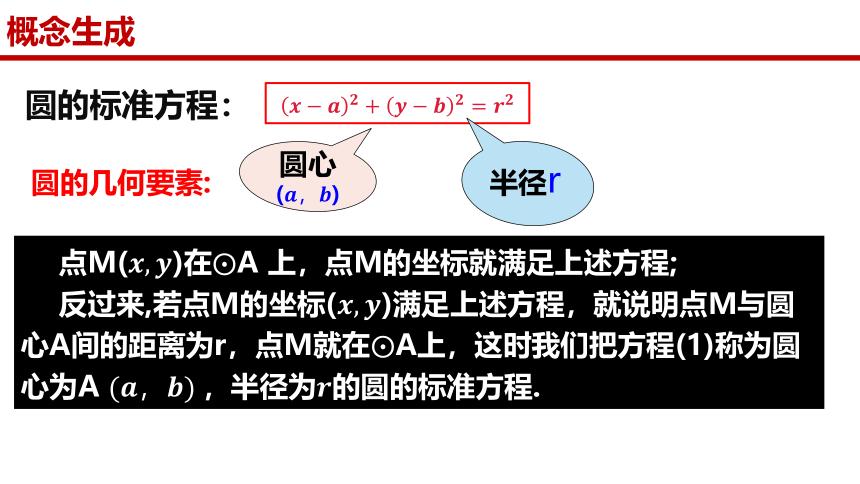
圆的标准方程:
圆心
()
半径r
圆的几何要素:
点M()在A 上,点M的坐标就满足上述方程;
反过来,若点M的坐标()满足上述方程,就说明点M与圆心A间的距离为r,点M就在A上,这时我们把方程(1)称为圆心为A ,半径为的圆的标准方程.
新知讲解
追问1 圆心在坐标原点,半径为的圆的标准方程是什么?
概念生成
建:建立坐标系
设:用坐标表示有关的量
限:限制条件
代:进行有关代数运算
化:化简
求点M的轨迹方程方法:
这也是求轨迹方程的步骤!
新知探究
探究二:求圆的标准方程
课堂练习
例1 求圆心为,半径为5的圆的标准方程,并判断点是否在这个圆上.
解:圆心为A(2,3) ,半径为5的圆的标准方程是
.
把点的坐标代入方程的左边,得,点M的坐标满足圆的方程,所以点在这个圆上.
把点的坐标代人方程的左边,得,点的坐标不满足圆的方程,所以点不在这个圆上
,两个点中,一个在圆上,一个点在圆内;
那我们该如何判断点与圆的位置关系?
新知探究
探究二:点与圆的位置关系
新知讲解
问题4 点 在圆内的条件是什么?在圆外的条件又是什么?
点 在圆上
新知讲解
点 在圆内
点 在圆外
判断d与r的关系,d为定点与圆心的距离。
概念生成
判断点与圆的位置关系与的关系:
(1),点在圆上
(2),点在圆外
(3),点在圆内
d为定点与圆心的距离,r为半径
新知探究
探究三:根据条件求取圆的标准方程
课堂练习
例2 已知圆心为C的圆经过两点,且圆心在直线上,求此圆的标准方程.
分析:不在同一条直线上的三个点可以确定一个圆,三角形有唯一的外接圆.显然已知的三个点不在同一条直线上,只要确定了a,b,r,圆的标准方程就确定了.
习题讲解
解:设所求的方程是 ①.
因为A(5,1),B(7,3),C(2,8)三点都在圆上,所以它们的坐标都满足方程①.于是,.
观察上面的式子,我们发现,三式两两相减,可以消去,,,得到关于,的二元一次方程组,解此方程组,得,
代人,得=25.
所以,ABC的外接圆的标准方程是.
利用待定系数法求圆的方程
ABC的外接圆的圆心是ABC的外心,即ABC三边垂直平分线的交点.
课堂练习
例3 已知圆心为C的圆经过两点,且圆心C在直线上,求此圆的标准方程.
分析:设圆心C的坐标为. 由已知条件可知,|CA|=|CB|,且.由此可求出圆心坐标和半径.
设圆心C的坐标为(a,b).因为圆心C在直线l:上
所以.
因为A,B是圆上两点,所以.根据两点间距离公式,有,
即.
由①②可得,.
所以圆心C的坐标是(,).
圆的半径.
所以,所求圆的标准方程是.
另外,因为线段AB是圆的一条弦,根据平面几何知识,AB的中点与圆心C的连线垂直于AB,由此可得到另一种解法.
习题讲解
如图,设线段AB的中点为D. 由A,B两点的坐标为(1,1),,可得点D的坐标为(),直线AB的斜率为.
因此,线段AB的垂直平分线l’的方程是,即.
由垂径定理可知,圆心C也在线段AB的垂直平分线上,所以它的坐标是方程组的解,得,所以圆心C的坐标是.
圆的半径.
所以,所求圆的标准方程是.
认真分析
数形结合
习题小结
圆的标准方程的两种求法
(1)几何法 它是利用图形的几何性质,如圆的性质等,直接求出圆的圆心和半径,代入圆的标准方程,从而得到圆的标准方程.
(2)待定系数法
由三个独立条件得到三个方程,解方程组以得到圆的标准方程中三个参数,从而确定圆的标准方程.它是求圆的方程最常用的方法,一般步骤是:
①设——设所求圆的方程为;
②列——由已知条件,建立关于的方程组;
③解——解方程组,求出;
④代——将代入所设方程,得所求圆的方程.
随堂练习
1.写出下列圆的标准方程:
(1)圆心为C(3,4),半径是;
(2)圆心为C(8,3),且经过点M(5,1).
解析:(1)
(2).
随堂练习
3.已知(4,9),(6,3)两点,求以线段为直径的圆的标准方程,并判断点在圆上、圆内,还是在圆外.
解析:设圆的标准方程为(r>0) ,则圆心为(),半径为r,
由题意得,,.
故所求圆的标准方程为.
将M(6,9),N(3,3),Q(5,3)的坐标分别代人圆的标准方程可得:
,点M在圆上;
,点N在圆外;
, 点Q在圆内.
随堂练习
4.已知△AOB 的三个顶点分别是点,求△AOB的外接圆的标准方程.
解析:设圆的标准方程为(r>0)
A(4,0),O(0,0),B(0,3)都在圆上,
,解得.
AOB外接圆的标准方程是.
待定系数法
小结
圆的标准方程:
判断点与圆的位置关系与的关系:
(1),点在圆上
(2),点在圆外
(3),点在圆内
d为定点与圆心的距离,r为半径
2.4圆的方程
直线与圆的方程
2.4.1圆的标准方程
课程标准
回顾确定圆的几何要素,在平面直角坐标系中,探索与掌握圆的标准方程
新课导入
多边形和圆是平面几何中的两类基本图形.
建立直线的方程后,我们可以运用它研究多边形这些“直线形”,解决边所在直线的平行或垂直、边与边的交点以及点到线段所在直线的距离等问题.
类似地,为了研究圆的有关性质,解决与圆有关的问题,我们首先需要建立圆的方程.
一
二
三
教学目标
掌握圆的定义及其标准方程
会根据圆的标准方程,掌握圆的标准方程的特征
会用待定系数法求圆的标准方程,判断点与圆的位置关系
教学目标
难点
重点
新知探究
探究一:圆的标准方程
新知讲解
问题1 在平面直角坐标系中,如何确定一个圆呢?
换句话说:圆的定义是什么?
类似于直线方程的建立过程,为建立圆的方程,我们首先考虑确定一个圆的几何要素.
圆是平面上到定点的距离等于定长的点的集合.
新知讲解
追问1 在平面直角坐标系中,如何确定一个圆呢?
在平面直角坐标系中,如果一个圆的圆心坐标和半径确定了,圆就唯一确定了.
由此,我们可以建立圆上点的坐标应满足的关系式,进而得到圆的方程.
A
M
r
O
下面我们就开始探究圆的标准方程
新知讲解
问题2 圆的标准方程是什么?
建:建立直角坐标系
假设:点M的坐标为
如图,在平面直角坐标系中,A 的圆心A的坐标为,半径为,为圆上任意一点,A就是以下点的集合.
设:用坐标表示有关的量
限:限制条件
代:进行有关代数运算
化:化简
根据两点间的距离公式
点M的坐标满足的条件可以表示为,
两边平方,得
概念生成
圆的标准方程:
圆心
()
半径r
圆的几何要素:
点M()在A 上,点M的坐标就满足上述方程;
反过来,若点M的坐标()满足上述方程,就说明点M与圆心A间的距离为r,点M就在A上,这时我们把方程(1)称为圆心为A ,半径为的圆的标准方程.
新知讲解
追问1 圆心在坐标原点,半径为的圆的标准方程是什么?
概念生成
建:建立坐标系
设:用坐标表示有关的量
限:限制条件
代:进行有关代数运算
化:化简
求点M的轨迹方程方法:
这也是求轨迹方程的步骤!
新知探究
探究二:求圆的标准方程
课堂练习
例1 求圆心为,半径为5的圆的标准方程,并判断点是否在这个圆上.
解:圆心为A(2,3) ,半径为5的圆的标准方程是
.
把点的坐标代入方程的左边,得,点M的坐标满足圆的方程,所以点在这个圆上.
把点的坐标代人方程的左边,得,点的坐标不满足圆的方程,所以点不在这个圆上
,两个点中,一个在圆上,一个点在圆内;
那我们该如何判断点与圆的位置关系?
新知探究
探究二:点与圆的位置关系
新知讲解
问题4 点 在圆内的条件是什么?在圆外的条件又是什么?
点 在圆上
新知讲解
点 在圆内
点 在圆外
判断d与r的关系,d为定点与圆心的距离。
概念生成
判断点与圆的位置关系与的关系:
(1),点在圆上
(2),点在圆外
(3),点在圆内
d为定点与圆心的距离,r为半径
新知探究
探究三:根据条件求取圆的标准方程
课堂练习
例2 已知圆心为C的圆经过两点,且圆心在直线上,求此圆的标准方程.
分析:不在同一条直线上的三个点可以确定一个圆,三角形有唯一的外接圆.显然已知的三个点不在同一条直线上,只要确定了a,b,r,圆的标准方程就确定了.
习题讲解
解:设所求的方程是 ①.
因为A(5,1),B(7,3),C(2,8)三点都在圆上,所以它们的坐标都满足方程①.于是,.
观察上面的式子,我们发现,三式两两相减,可以消去,,,得到关于,的二元一次方程组,解此方程组,得,
代人,得=25.
所以,ABC的外接圆的标准方程是.
利用待定系数法求圆的方程
ABC的外接圆的圆心是ABC的外心,即ABC三边垂直平分线的交点.
课堂练习
例3 已知圆心为C的圆经过两点,且圆心C在直线上,求此圆的标准方程.
分析:设圆心C的坐标为. 由已知条件可知,|CA|=|CB|,且.由此可求出圆心坐标和半径.
设圆心C的坐标为(a,b).因为圆心C在直线l:上
所以.
因为A,B是圆上两点,所以.根据两点间距离公式,有,
即.
由①②可得,.
所以圆心C的坐标是(,).
圆的半径.
所以,所求圆的标准方程是.
另外,因为线段AB是圆的一条弦,根据平面几何知识,AB的中点与圆心C的连线垂直于AB,由此可得到另一种解法.
习题讲解
如图,设线段AB的中点为D. 由A,B两点的坐标为(1,1),,可得点D的坐标为(),直线AB的斜率为.
因此,线段AB的垂直平分线l’的方程是,即.
由垂径定理可知,圆心C也在线段AB的垂直平分线上,所以它的坐标是方程组的解,得,所以圆心C的坐标是.
圆的半径.
所以,所求圆的标准方程是.
认真分析
数形结合
习题小结
圆的标准方程的两种求法
(1)几何法 它是利用图形的几何性质,如圆的性质等,直接求出圆的圆心和半径,代入圆的标准方程,从而得到圆的标准方程.
(2)待定系数法
由三个独立条件得到三个方程,解方程组以得到圆的标准方程中三个参数,从而确定圆的标准方程.它是求圆的方程最常用的方法,一般步骤是:
①设——设所求圆的方程为;
②列——由已知条件,建立关于的方程组;
③解——解方程组,求出;
④代——将代入所设方程,得所求圆的方程.
随堂练习
1.写出下列圆的标准方程:
(1)圆心为C(3,4),半径是;
(2)圆心为C(8,3),且经过点M(5,1).
解析:(1)
(2).
随堂练习
3.已知(4,9),(6,3)两点,求以线段为直径的圆的标准方程,并判断点在圆上、圆内,还是在圆外.
解析:设圆的标准方程为(r>0) ,则圆心为(),半径为r,
由题意得,,.
故所求圆的标准方程为.
将M(6,9),N(3,3),Q(5,3)的坐标分别代人圆的标准方程可得:
,点M在圆上;
,点N在圆外;
, 点Q在圆内.
随堂练习
4.已知△AOB 的三个顶点分别是点,求△AOB的外接圆的标准方程.
解析:设圆的标准方程为(r>0)
A(4,0),O(0,0),B(0,3)都在圆上,
,解得.
AOB外接圆的标准方程是.
待定系数法
小结
圆的标准方程:
判断点与圆的位置关系与的关系:
(1),点在圆上
(2),点在圆外
(3),点在圆内
d为定点与圆心的距离,r为半径
