2.5解直角三角形的应用(2)课件(共18张PPT)
文档属性
| 名称 | 2.5解直角三角形的应用(2)课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 312.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 17:57:10 | ||
图片预览






文档简介
(共18张PPT)
青岛版 数学 九(上) 第2章 解直角三角形
§2.5解直角三角形的应用(2)
tanA=
b
a
∠A + ∠B = 90 °;
勾股定理:a2+b2=c2 ;
(3)角与边之间的关系:
(2)边之间的关系:
(1)角之间的关系:
sinA=
c
a
,
cosA=
c
b
,
2. 如果知道直角三角形的几个元素就可以求其
他的元素?有几种情况?
两个元素(至少一个是边)
两条边或一边一角
1.直角三角形的边角关系:
复习回顾
4.解决实际问题的思路是:
从高处观测低处的目标时,视线与水平线所成的锐角叫做俯角.
从低处观测高处的目标时,视线与水平线所成的锐角叫做仰角;
3、什么叫仰角、俯角?
复习回顾
先把实际问题中的仰角、俯角转化到图形(特别是三角形)中,然后再利用解直角三角形的方法思路解答。
加油站
1、方位角:
如右图所示,在点O观测,
A在北偏东70°方向;
B在南偏东15°方向;
C在南偏西35°方向;
D在北偏西40°方向。
东
北
O
A
B
C
D
70°
15°
35°
40°
2、东北方向即为北偏东45°方向;
东南方向即为______________;
西北方向即为______________;
西南方向即为_______________.
南偏东45°方向
北偏西45°方向
南偏西45°方向
A
·
60°
B
C
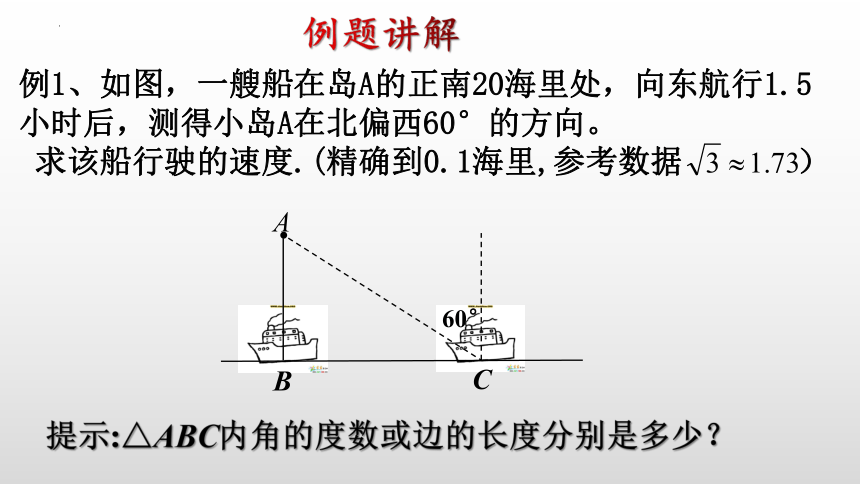
例题讲解
例1、如图,一艘船在岛A的正南20海里处,向东航行1.5小时后,测得小岛A在北偏西60°的方向。
求该船行驶的速度.(精确到0.1海里,参考数据 )
提示:△ABC内角的度数或边的长度分别是多少?
A
·
60°
B
C
解:由题意,得
例2、如图,一轮船在A处测得北偏东45°方向有一座灯塔B,轮船沿正东方向以18海里/时的速度航行,1时30分后到达点C,这时测得灯塔B在北偏东15°方向。
求:灯塔B到点C的距离(精确到0.1海里).
A
C
B
45°
15°
D
例题讲解
提示:△ABC内角的度数或边的长度分别是多少?
A
C
B
45°
15°
D
例3、如图所示,A,B是两座现代化的城市,C是一个古城遗址,C城在A城的北偏东30°,在B城的西北方向,且C城与A城相距120千米,B城在A城的正东方向。以点C为圆心,以60千米为半径的圆形区域内有古迹和地下文物,现要在A,B两城之间修一条笔直的高速公路。
(1)请分析这条公路是否对文物古迹造成损毁;
(2)并计算公路的长度。(结果保留根号)
A
B
C
30°
45°
例题讲解
D
┏
提示:
△ABC内角的度数或边的长度分别
是多少?
A
B
C
30°
45°
D
┏
∴这条公路不会对文物古迹
造成损毁
A
B
C
30°
45°
D
┏
A
C
B
例4、如图,建筑物C在观测点A的北偏东65°方向上,
从观测点A出发向南偏东40°方向走了130米到达观测
点B,此时测得建筑物C在观测点B的北偏东20°方向上,
求:观测点B与建筑物C之间的距离。(结果精确到0.1
米,参考数据 )
例题讲解
提示:
△ABC内角的度数或边的长度分别
是多少?
D
┏
A
C
B
D
┏
例题讲解
例5、如图,A、B、C三地在同一直线上,D地在A地的北偏东30°方向上,在C地的北偏西45°方向上,C地在A地的北偏东75°方向上,且BD=BC=40米, 求:A地到D地的距离。(结果保留根号)
A
C
B
D
提示:
(1)△ADC中,能已知哪些内角的度数?
(2)△BDC是什么形状的三角形?
(3)过哪个点引垂线?
E
┏
A
C
B
D
E
┏
课堂小结
1、方位角:
2、东北方向、东南方向、西北方向、
西南方向的方位角:
3.解决实际问题的思路是:
先把实际问题中的方位角转化到图形(特别是三角形)中,然后再利用解直角三角形的方法思路解答。
作业
课本P57 2 题
同学们,
再见!
青岛版 数学 九(上) 第2章 解直角三角形
§2.5解直角三角形的应用(2)
tanA=
b
a
∠A + ∠B = 90 °;
勾股定理:a2+b2=c2 ;
(3)角与边之间的关系:
(2)边之间的关系:
(1)角之间的关系:
sinA=
c
a
,
cosA=
c
b
,
2. 如果知道直角三角形的几个元素就可以求其
他的元素?有几种情况?
两个元素(至少一个是边)
两条边或一边一角
1.直角三角形的边角关系:
复习回顾
4.解决实际问题的思路是:
从高处观测低处的目标时,视线与水平线所成的锐角叫做俯角.
从低处观测高处的目标时,视线与水平线所成的锐角叫做仰角;
3、什么叫仰角、俯角?
复习回顾
先把实际问题中的仰角、俯角转化到图形(特别是三角形)中,然后再利用解直角三角形的方法思路解答。
加油站
1、方位角:
如右图所示,在点O观测,
A在北偏东70°方向;
B在南偏东15°方向;
C在南偏西35°方向;
D在北偏西40°方向。
东
北
O
A
B
C
D
70°
15°
35°
40°
2、东北方向即为北偏东45°方向;
东南方向即为______________;
西北方向即为______________;
西南方向即为_______________.
南偏东45°方向
北偏西45°方向
南偏西45°方向
A
·
60°
B
C
例题讲解
例1、如图,一艘船在岛A的正南20海里处,向东航行1.5小时后,测得小岛A在北偏西60°的方向。
求该船行驶的速度.(精确到0.1海里,参考数据 )
提示:△ABC内角的度数或边的长度分别是多少?
A
·
60°
B
C
解:由题意,得
例2、如图,一轮船在A处测得北偏东45°方向有一座灯塔B,轮船沿正东方向以18海里/时的速度航行,1时30分后到达点C,这时测得灯塔B在北偏东15°方向。
求:灯塔B到点C的距离(精确到0.1海里).
A
C
B
45°
15°
D
例题讲解
提示:△ABC内角的度数或边的长度分别是多少?
A
C
B
45°
15°
D
例3、如图所示,A,B是两座现代化的城市,C是一个古城遗址,C城在A城的北偏东30°,在B城的西北方向,且C城与A城相距120千米,B城在A城的正东方向。以点C为圆心,以60千米为半径的圆形区域内有古迹和地下文物,现要在A,B两城之间修一条笔直的高速公路。
(1)请分析这条公路是否对文物古迹造成损毁;
(2)并计算公路的长度。(结果保留根号)
A
B
C
30°
45°
例题讲解
D
┏
提示:
△ABC内角的度数或边的长度分别
是多少?
A
B
C
30°
45°
D
┏
∴这条公路不会对文物古迹
造成损毁
A
B
C
30°
45°
D
┏
A
C
B
例4、如图,建筑物C在观测点A的北偏东65°方向上,
从观测点A出发向南偏东40°方向走了130米到达观测
点B,此时测得建筑物C在观测点B的北偏东20°方向上,
求:观测点B与建筑物C之间的距离。(结果精确到0.1
米,参考数据 )
例题讲解
提示:
△ABC内角的度数或边的长度分别
是多少?
D
┏
A
C
B
D
┏
例题讲解
例5、如图,A、B、C三地在同一直线上,D地在A地的北偏东30°方向上,在C地的北偏西45°方向上,C地在A地的北偏东75°方向上,且BD=BC=40米, 求:A地到D地的距离。(结果保留根号)
A
C
B
D
提示:
(1)△ADC中,能已知哪些内角的度数?
(2)△BDC是什么形状的三角形?
(3)过哪个点引垂线?
E
┏
A
C
B
D
E
┏
课堂小结
1、方位角:
2、东北方向、东南方向、西北方向、
西南方向的方位角:
3.解决实际问题的思路是:
先把实际问题中的方位角转化到图形(特别是三角形)中,然后再利用解直角三角形的方法思路解答。
作业
课本P57 2 题
同学们,
再见!
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
