人教版(新)七上-4.1.1 立体图形与平面图形 第四课时【优质课件】
文档属性
| 名称 | 人教版(新)七上-4.1.1 立体图形与平面图形 第四课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 14:27:48 | ||
图片预览





文档简介
(共28张PPT)
4.1.1 立体图形
与平面图形
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
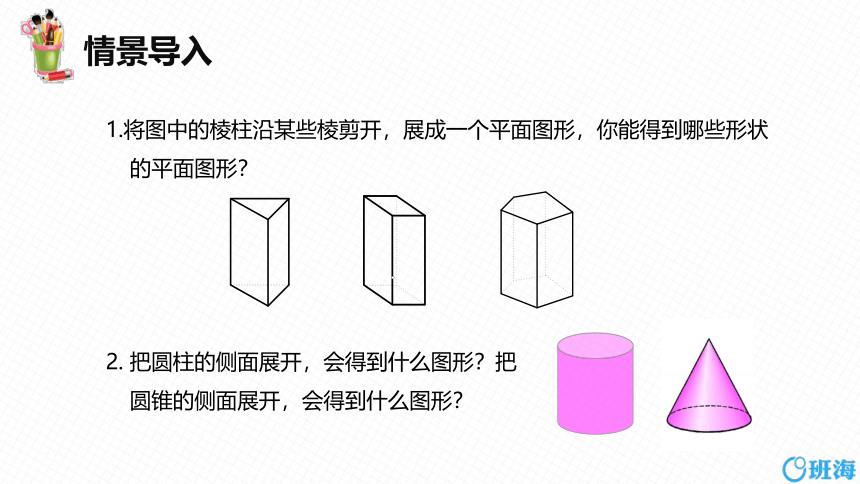
1.将图中的棱柱沿某些棱剪开,展成一个平面图形,你能得到哪些形状的平面图形?
2. 把圆柱的侧面展开,会得到什么图形?把
圆锥的侧面展开,会得到什么图形?
新课精讲
探索新知
1
知识点
柱体的展开与折叠
探索新知
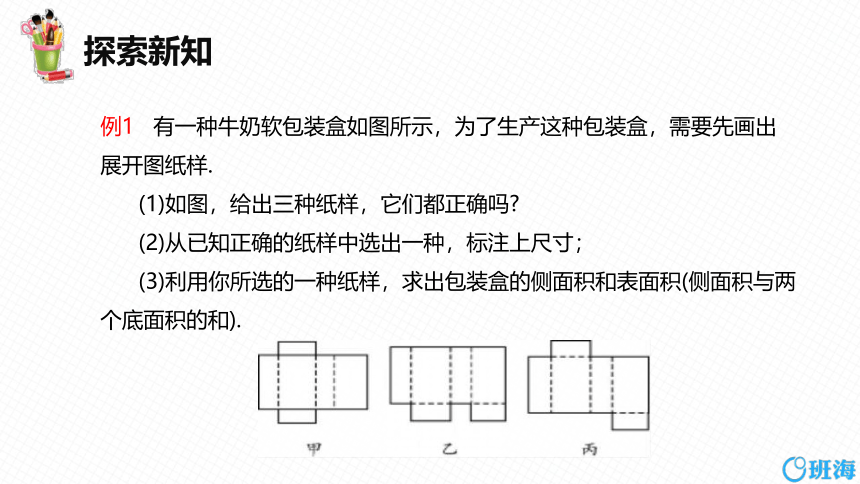
例1 有一种牛奶软包装盒如图所示,为了生产这种包装盒,需要先画出展开图纸样.
(1)如图,给出三种纸样,它们都正确吗
(2)从已知正确的纸样中选出一种,标注上尺寸;
(3)利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和).
探索新知
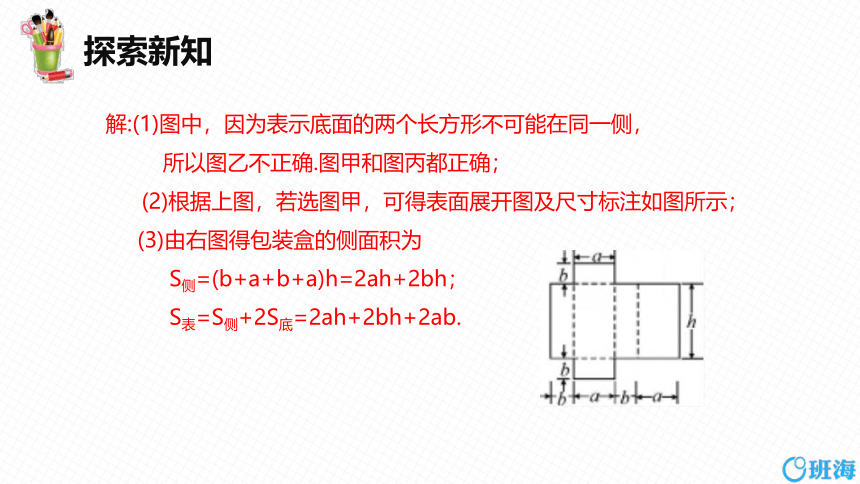
解:(1)图中,因为表示底面的两个长方形不可能在同一侧,
所以图乙不正确.图甲和图丙都正确;
(2)根据上图,若选图甲,可得表面展开图及尺寸标注如图所示;
(3)由右图得包装盒的侧面积为
S侧=(b+a+b+a)h=2ah+2bh;
S表=S侧+2S底=2ah+2bh+2ab.
典题精讲
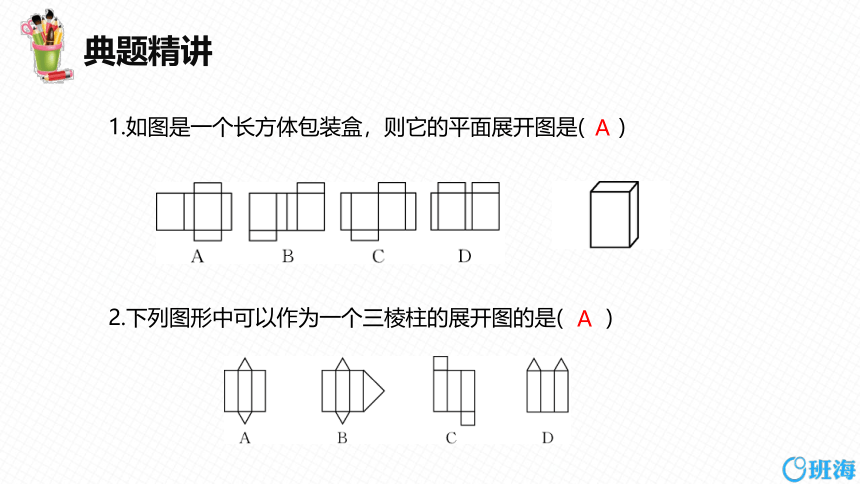
1.如图是一个长方体包装盒,则它的平面展开图是( )
2.下列图形中可以作为一个三棱柱的展开图的是( )
A
A
探索新知
2
知识点
锥体的展开与折叠
下列图形能折叠成什么图形?
圆柱
五棱柱
圆锥
三棱柱
探索新知
解:圆锥、圆柱的展开图如下:
例2 如图,将下列两个图形沿AB剪开,再展开,实际动手做一做,再对照实物画出展开后的图形.
探索新知
总 结
圆锥的侧面展开图是一个扇形,底面是一个圆.
圆柱的侧面展开图是一个矩形,两底面是两个等圆.
由此我们可以了解组成圆锥和圆柱的基本图形.
探索新知
例3 如图是一个长方体纸盒的展开图,求这个纸盒的表面积和体积.(纸的厚度不计) (单位:厘米)
解:高为:(40-20)÷2=10(厘米),
表面积为:20×15×2+20×10×2+15×10×2
=600+400+300
=1 300(平方厘米);
体积为:20×15×10=3 000(立方厘米).
答:长方体的表面积为1 300平方厘米,
体积为3 000立方厘米.
探索新知
例4 一个正棱柱(底面为正多边形),它有30条棱,侧棱长为10 cm,
底面边长为1 cm.
(1)这是几棱柱?
(2)此棱柱的侧面积是多少?
解:30÷3=10,是十棱柱.
解: 10×1×10=100(cm2).
典题精讲
1.如图是一个圆锥,下列平面图形既不是它的三视图,
也不是它的侧面展开图的是( )
D
典题精讲
2.一个几何体的表面展开图如图所示,则这个几何体是( )
A.四棱锥
B.四棱柱
C.三棱锥
D.三棱柱
A
学以致用
小试牛刀
1.如图是一个长方体包装盒,则它的平面展开图是( )
A.
B.
C.
D.
A
小试牛刀
2.下列图形中可以作为一个=棱柱的展开图的是( )
A. B.
C. D.
A
小试牛刀
3.如图,圆柱体的表面展开后得到的平面图形是( )
A.
B.
C.
D.
B
小试牛刀
4.如图是一个圆锥,下列平面图形既不是从不同方向看它得到的平面图
形,也不是它的侧面展开图的是( )
A.
B.
C.
D.
D
小试牛刀
5.将图①的正四棱锥A-BCDE沿着其中的四个边剪开后,形成的展开图
为图②,判断下列哪一个选项中的四个边可为此四个边 ( )
A.AC、AD、BC、DE
B.AB、BE、DE、CD
C.AC、BC、AE、DE
D.AC、AD、AE、BC
A
小试牛刀
6.在如图所示的图形中,是三棱柱的展开图的有( )
A.1个 B. 2个 C. 3个 D. 4个
B
小试牛刀
7.如图是一个长方体纸盒的展开图,求这个纸盒的表面积和体积.
(纸的厚度不计)(单位:厘米)
解:(40一20)÷2=10(厘米),
表面积为:20×15×2+20×10×2+15×10×2
=600+400+300=1300(平方厘米),
体积为:20×15×10=3(立方厘米).
答·纸盒的表面积为1300平方厘米,体积为3000立方厘米.
小试牛刀
8.一个正棱柱(底面为正多边形),它有30条棱,侧棱长为10cm,底
面边长为1cm.
(1)这是几棱柱?
30÷3:10,是十棱柱.
(2)此棱柱的侧面积是多少?
10×1×10:100(cm )
课堂小结
课堂小结
正方体、棱锥、棱柱展开图的基本条件:
一般地,如果某立体图形的表面展开图由6个正方形组合而成,那么立体图形是正方体;如果是由3个及3个以上的三角形与1个多边形组合而成的,那么立体图形为棱锥;如果是由3个及3个以上的长方形与两个形状、大小都相同的多边形组合而成的,那么立体图形为棱柱.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
4.1.1 立体图形
与平面图形
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.将图中的棱柱沿某些棱剪开,展成一个平面图形,你能得到哪些形状的平面图形?
2. 把圆柱的侧面展开,会得到什么图形?把
圆锥的侧面展开,会得到什么图形?
新课精讲
探索新知
1
知识点
柱体的展开与折叠
探索新知
例1 有一种牛奶软包装盒如图所示,为了生产这种包装盒,需要先画出展开图纸样.
(1)如图,给出三种纸样,它们都正确吗
(2)从已知正确的纸样中选出一种,标注上尺寸;
(3)利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和).
探索新知
解:(1)图中,因为表示底面的两个长方形不可能在同一侧,
所以图乙不正确.图甲和图丙都正确;
(2)根据上图,若选图甲,可得表面展开图及尺寸标注如图所示;
(3)由右图得包装盒的侧面积为
S侧=(b+a+b+a)h=2ah+2bh;
S表=S侧+2S底=2ah+2bh+2ab.
典题精讲
1.如图是一个长方体包装盒,则它的平面展开图是( )
2.下列图形中可以作为一个三棱柱的展开图的是( )
A
A
探索新知
2
知识点
锥体的展开与折叠
下列图形能折叠成什么图形?
圆柱
五棱柱
圆锥
三棱柱
探索新知
解:圆锥、圆柱的展开图如下:
例2 如图,将下列两个图形沿AB剪开,再展开,实际动手做一做,再对照实物画出展开后的图形.
探索新知
总 结
圆锥的侧面展开图是一个扇形,底面是一个圆.
圆柱的侧面展开图是一个矩形,两底面是两个等圆.
由此我们可以了解组成圆锥和圆柱的基本图形.
探索新知
例3 如图是一个长方体纸盒的展开图,求这个纸盒的表面积和体积.(纸的厚度不计) (单位:厘米)
解:高为:(40-20)÷2=10(厘米),
表面积为:20×15×2+20×10×2+15×10×2
=600+400+300
=1 300(平方厘米);
体积为:20×15×10=3 000(立方厘米).
答:长方体的表面积为1 300平方厘米,
体积为3 000立方厘米.
探索新知
例4 一个正棱柱(底面为正多边形),它有30条棱,侧棱长为10 cm,
底面边长为1 cm.
(1)这是几棱柱?
(2)此棱柱的侧面积是多少?
解:30÷3=10,是十棱柱.
解: 10×1×10=100(cm2).
典题精讲
1.如图是一个圆锥,下列平面图形既不是它的三视图,
也不是它的侧面展开图的是( )
D
典题精讲
2.一个几何体的表面展开图如图所示,则这个几何体是( )
A.四棱锥
B.四棱柱
C.三棱锥
D.三棱柱
A
学以致用
小试牛刀
1.如图是一个长方体包装盒,则它的平面展开图是( )
A.
B.
C.
D.
A
小试牛刀
2.下列图形中可以作为一个=棱柱的展开图的是( )
A. B.
C. D.
A
小试牛刀
3.如图,圆柱体的表面展开后得到的平面图形是( )
A.
B.
C.
D.
B
小试牛刀
4.如图是一个圆锥,下列平面图形既不是从不同方向看它得到的平面图
形,也不是它的侧面展开图的是( )
A.
B.
C.
D.
D
小试牛刀
5.将图①的正四棱锥A-BCDE沿着其中的四个边剪开后,形成的展开图
为图②,判断下列哪一个选项中的四个边可为此四个边 ( )
A.AC、AD、BC、DE
B.AB、BE、DE、CD
C.AC、BC、AE、DE
D.AC、AD、AE、BC
A
小试牛刀
6.在如图所示的图形中,是三棱柱的展开图的有( )
A.1个 B. 2个 C. 3个 D. 4个
B
小试牛刀
7.如图是一个长方体纸盒的展开图,求这个纸盒的表面积和体积.
(纸的厚度不计)(单位:厘米)
解:(40一20)÷2=10(厘米),
表面积为:20×15×2+20×10×2+15×10×2
=600+400+300=1300(平方厘米),
体积为:20×15×10=3(立方厘米).
答·纸盒的表面积为1300平方厘米,体积为3000立方厘米.
小试牛刀
8.一个正棱柱(底面为正多边形),它有30条棱,侧棱长为10cm,底
面边长为1cm.
(1)这是几棱柱?
30÷3:10,是十棱柱.
(2)此棱柱的侧面积是多少?
10×1×10:100(cm )
课堂小结
课堂小结
正方体、棱锥、棱柱展开图的基本条件:
一般地,如果某立体图形的表面展开图由6个正方形组合而成,那么立体图形是正方体;如果是由3个及3个以上的三角形与1个多边形组合而成的,那么立体图形为棱锥;如果是由3个及3个以上的长方形与两个形状、大小都相同的多边形组合而成的,那么立体图形为棱柱.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
