人教版(新)七上-4.1.2 点、线、面、体【优质课件】
文档属性
| 名称 | 人教版(新)七上-4.1.2 点、线、面、体【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览









文档简介
(共36张PPT)
4.1.2
点、线、面、体
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
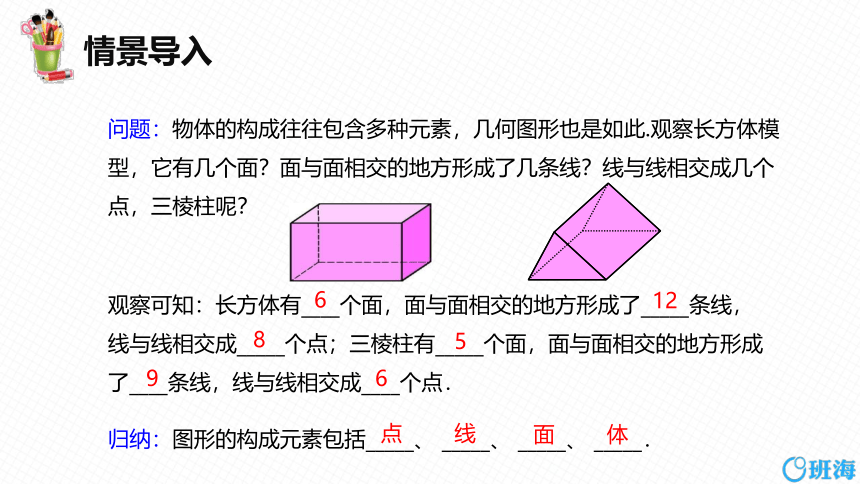
问题:物体的构成往往包含多种元素,几何图形也是如此.观察长方体模型,它有几个面?面与面相交的地方形成了几条线?线与线相交成几个点,三棱柱呢?
观察可知:长方体有____个面,面与面相交的地方形成了_____条线,线与线相交成_____个点;三棱柱有_____个面,面与面相交的地方形成了____条线,线与线相交成____个点.
6
12
8
5
9
6
归纳:图形的构成元素包括_____、 _____、 _____、 _____.
点
线
面
体
新课精讲
探索新知
1
知识点
构成图形的元素
1.点、线、面、体的关系:几何体简称体,包围着体的是面,面和面相交的地方形成线,线和线相交的地方形成点.点动成线,线动成面,面动成体.
2.几何图形都是由点、线、面、体组成的,点是构成图形的基本元素.
探索新知
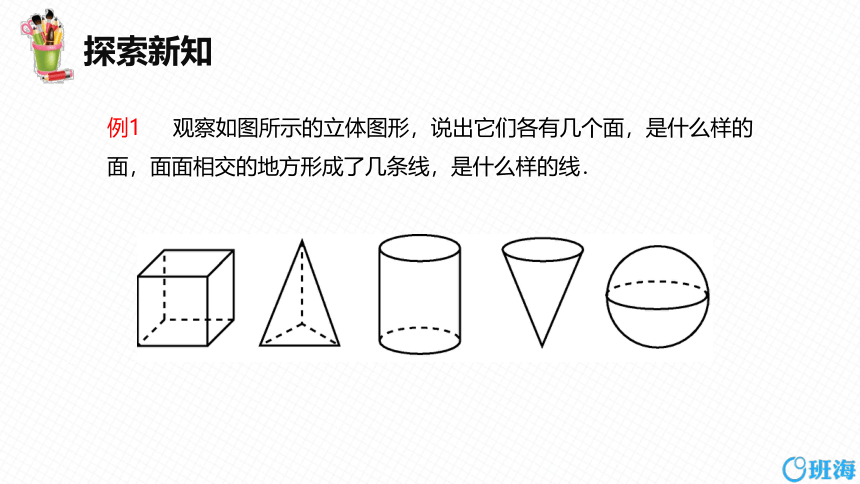
例1 观察如图所示的立体图形,说出它们各有几个面,是什么样的面,面面相交的地方形成了几条线,是什么样的线.
探索新知
导引:清楚点、线、面、体的关系是解决本题的关键.包围体的是面,面和面相交的地方形成线.
解:正方体有6个平面,面面相交形成12条线,都是直线.
三棱锥有4个平面,面面相交形成6条线,都是直线.
圆柱有3个面,2个平面和1个曲面,面面相交形成2条曲线.
圆锥有2个面,1个平面和1个曲面,面面相交形成1条曲线.
球只有1个曲面.
探索新知
总 结
点、线、面、体与几何图形关系:
(静态)面面相交——线,线线相交——点,
(动态)点动成线,线动成面,面动成体.
典题精讲
1.下面几何体中,全是由曲面围成的是( )
A.圆锥 B.正方体
C.圆柱 D.球
2.在球、圆锥、圆柱、棱柱中,由曲面和平面围成的是( )
A.球和圆锥 B.球和圆柱
C.圆锥和圆柱 D.圆柱和棱柱
D
C
探索新知
2
知识点
图形的形成方法
探索新知
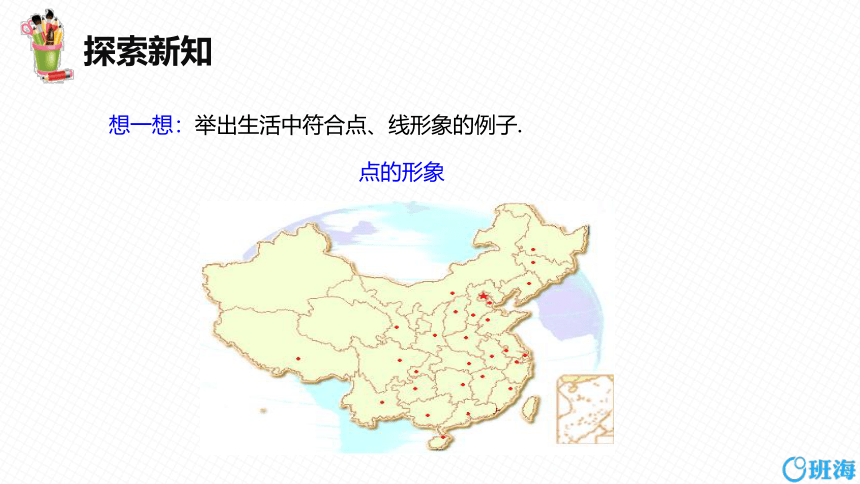
点的形象
想一想:举出生活中符合点、线形象的例子.
探索新知
线的形象
探索新知
观察这些面,它们有区别吗?
面是有区别的,可以分为平面和曲面;围成体的面只是平面或曲面的一部分.
探索新知
你能从下面几何体中找出点、线、面吗?
思考:体是由什么围成的?它们有什么不同?
体是由面组成,面与面相交成线,线与线相交成点
探索新知
物体的运动会留下运动轨迹,这些运动轨迹往往也能抽象成几何图形.如果把笔尖看成一个点,这个点在纸上运动时,形成的图形是什么 动手试一试.
归纳结论:
点动成线.
探索新知
举出生活中能够说明“点动成线”这一结论的例子.
探索新知
汽车的雨刷在挡风玻璃上画出一个扇面,从几何的角度观察这种现象,你可以得出什么结论?
线动成面.
概括结论:
探索新知
既然“点动成线,线动成面”,那么请同学们想一想:当面运动时又会形成什么图形?如何验证你的猜想?
概括结论:
面动成体.
探索新知
点 线 面 体
点动成线
面动成体
线动成面
线与线相交形成点
面与面相交形成线
包围着体的部分是面
探索新知
例2 笔尖在纸上快速滑动写出了一个又一个字,这说明了_________;
车轮旋转时,看起来像一个 整体的圆面,这说明了__________;直角三
角形绕它的一条直角边所在的直线旋转一周,形成了一个圆锥,这说明
了_________.
导引:构成图形的要素是点、线、面,其中点是构成图形的最基本元素,判断图形构成情况时,有三种情况:点动成线,线动成面,面动成体,通过实际情景,逐一分析便可得结果.
点动成线
线动成面
面动成体
探索新知
总 结
一个平面图形旋转后得到一个立体图形,这个立体图形的形状取决于两个因素:
(1)平面图形的形状;
(2)旋转时所绕的轴的位置.
典题精讲
1.下雨时,司机会打开雨刷器,雨刷器在运动时会形成一个扇面,这
是因为( )
A.点动成线 B.线动成面
C.面动成体 D.面面相交形成线
B
2.下列现象能说明“面动成体”的是( )
A.时钟的钟摆摆动的轨迹 B.旋转一扇门,门在空中运动的轨迹
C.扔出一块小石子,小石子在天空中飞行的路线
D.一根舞动的荧光棒
B
学以致用
小试牛刀
1.把如图所示的图形折成一个正方体的盒子,折好后与“中”相对的字
是( )
A.祝 B.你
C.顺 D.利
C
2.下列选项中的拼图,不是由图中这副七巧板拼成的是( )
B
小试牛刀
3.如图所示的几何体是由哪个图形绕虚线旋转一周形成的( )
A
小试牛刀
4.把如图①所示的正方体的展开图围成正方体(文字露在外面),再将这个
正方体按照如图②依次翻滚到第1格,第2格,第3格,第4格,此时正
方体朝上一面的文字为( )
A. 富 B.强
C.文 D.民
A
点拨:
由题图①可得,“富”和“文”相对;“强”和“主”相对,“民”和“明”相对;由题图②可得,小正方体从图②的位置依次翻到第4格时,“文”在下面,则这时小正方体朝上一面的文字是“富”.
小试牛刀
5.下列事实可以用“两点确定一条直线”来解释的有( )个.
①墙上钉木条至少要两个钉子才能牢固;②农民拉绳插秧;
③解放军叔叔打靶瞄准;④从A地到B地架设电线,总是尽可
能沿着线段AB架设.
A.1 B.2 C.3 D.4
C
点拨:
①②③现象可以用两点确定一条直线来解释;④现象可以用两点之间,线段最短来解释.
小试牛刀
6.下列现象中,可用基本事实“两点之间,线段最短”来解释的是( )
A.用两个钉子就可以把木条固定在墙上
B.把弯曲的公路改直,就能缩短路程
C.利用圆规可以比较两条线段的长短关系
D.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
B
小试牛刀
7.如图所示的图形中哪些图形是立体图形,哪些图形是平面图形?
解:
立体图形有:①④⑤⑥⑦
平面图形有:②③⑧
小试牛刀
8.如图,已知线段AD=10 cm,点B,C都是线段AD上的点,且AC=7 cm,BD=4 cm. 若点E,F分别是线段AB,CD的中点,求线段EF的长.
解:
因为点E,F分别是线段AB,CD的中点,
所以EF=BE+BC+CF= AB+BC+ CD
= AB+ CD+ BC+ BC
= (AB+BC+CD+BC)
= (AC+BD) = ×(7+4)= (cm).
小试牛刀
9.如图,已知AB和CD的公共部分BD= AB= CD,线段AB,CD的中点E,F之间的距离是10 cm,求AB,CD的长.
解:
因为BD= AB= CD,所以CD= AB.
因为F是CD的中点,
所以DF= CD= × AB= AB.
小试牛刀
因为E是AB的中点,所以EB= AB,
所以ED=EB-DB= AB- AB= AB.
所以EF=ED+DF= AB+ AB
= AB=10 cm,
所以AB=12 cm,
所以CD= AB=16 cm.
课堂小结
课堂小结
点、线、面、体及它们之间的关系.
点 线 面 体
点动成线
面动成体
线动成面
线与线相交形成点
面与面相交形成线
包围着体的部分是面
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
4.1.2
点、线、面、体
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
问题:物体的构成往往包含多种元素,几何图形也是如此.观察长方体模型,它有几个面?面与面相交的地方形成了几条线?线与线相交成几个点,三棱柱呢?
观察可知:长方体有____个面,面与面相交的地方形成了_____条线,线与线相交成_____个点;三棱柱有_____个面,面与面相交的地方形成了____条线,线与线相交成____个点.
6
12
8
5
9
6
归纳:图形的构成元素包括_____、 _____、 _____、 _____.
点
线
面
体
新课精讲
探索新知
1
知识点
构成图形的元素
1.点、线、面、体的关系:几何体简称体,包围着体的是面,面和面相交的地方形成线,线和线相交的地方形成点.点动成线,线动成面,面动成体.
2.几何图形都是由点、线、面、体组成的,点是构成图形的基本元素.
探索新知
例1 观察如图所示的立体图形,说出它们各有几个面,是什么样的面,面面相交的地方形成了几条线,是什么样的线.
探索新知
导引:清楚点、线、面、体的关系是解决本题的关键.包围体的是面,面和面相交的地方形成线.
解:正方体有6个平面,面面相交形成12条线,都是直线.
三棱锥有4个平面,面面相交形成6条线,都是直线.
圆柱有3个面,2个平面和1个曲面,面面相交形成2条曲线.
圆锥有2个面,1个平面和1个曲面,面面相交形成1条曲线.
球只有1个曲面.
探索新知
总 结
点、线、面、体与几何图形关系:
(静态)面面相交——线,线线相交——点,
(动态)点动成线,线动成面,面动成体.
典题精讲
1.下面几何体中,全是由曲面围成的是( )
A.圆锥 B.正方体
C.圆柱 D.球
2.在球、圆锥、圆柱、棱柱中,由曲面和平面围成的是( )
A.球和圆锥 B.球和圆柱
C.圆锥和圆柱 D.圆柱和棱柱
D
C
探索新知
2
知识点
图形的形成方法
探索新知
点的形象
想一想:举出生活中符合点、线形象的例子.
探索新知
线的形象
探索新知
观察这些面,它们有区别吗?
面是有区别的,可以分为平面和曲面;围成体的面只是平面或曲面的一部分.
探索新知
你能从下面几何体中找出点、线、面吗?
思考:体是由什么围成的?它们有什么不同?
体是由面组成,面与面相交成线,线与线相交成点
探索新知
物体的运动会留下运动轨迹,这些运动轨迹往往也能抽象成几何图形.如果把笔尖看成一个点,这个点在纸上运动时,形成的图形是什么 动手试一试.
归纳结论:
点动成线.
探索新知
举出生活中能够说明“点动成线”这一结论的例子.
探索新知
汽车的雨刷在挡风玻璃上画出一个扇面,从几何的角度观察这种现象,你可以得出什么结论?
线动成面.
概括结论:
探索新知
既然“点动成线,线动成面”,那么请同学们想一想:当面运动时又会形成什么图形?如何验证你的猜想?
概括结论:
面动成体.
探索新知
点 线 面 体
点动成线
面动成体
线动成面
线与线相交形成点
面与面相交形成线
包围着体的部分是面
探索新知
例2 笔尖在纸上快速滑动写出了一个又一个字,这说明了_________;
车轮旋转时,看起来像一个 整体的圆面,这说明了__________;直角三
角形绕它的一条直角边所在的直线旋转一周,形成了一个圆锥,这说明
了_________.
导引:构成图形的要素是点、线、面,其中点是构成图形的最基本元素,判断图形构成情况时,有三种情况:点动成线,线动成面,面动成体,通过实际情景,逐一分析便可得结果.
点动成线
线动成面
面动成体
探索新知
总 结
一个平面图形旋转后得到一个立体图形,这个立体图形的形状取决于两个因素:
(1)平面图形的形状;
(2)旋转时所绕的轴的位置.
典题精讲
1.下雨时,司机会打开雨刷器,雨刷器在运动时会形成一个扇面,这
是因为( )
A.点动成线 B.线动成面
C.面动成体 D.面面相交形成线
B
2.下列现象能说明“面动成体”的是( )
A.时钟的钟摆摆动的轨迹 B.旋转一扇门,门在空中运动的轨迹
C.扔出一块小石子,小石子在天空中飞行的路线
D.一根舞动的荧光棒
B
学以致用
小试牛刀
1.把如图所示的图形折成一个正方体的盒子,折好后与“中”相对的字
是( )
A.祝 B.你
C.顺 D.利
C
2.下列选项中的拼图,不是由图中这副七巧板拼成的是( )
B
小试牛刀
3.如图所示的几何体是由哪个图形绕虚线旋转一周形成的( )
A
小试牛刀
4.把如图①所示的正方体的展开图围成正方体(文字露在外面),再将这个
正方体按照如图②依次翻滚到第1格,第2格,第3格,第4格,此时正
方体朝上一面的文字为( )
A. 富 B.强
C.文 D.民
A
点拨:
由题图①可得,“富”和“文”相对;“强”和“主”相对,“民”和“明”相对;由题图②可得,小正方体从图②的位置依次翻到第4格时,“文”在下面,则这时小正方体朝上一面的文字是“富”.
小试牛刀
5.下列事实可以用“两点确定一条直线”来解释的有( )个.
①墙上钉木条至少要两个钉子才能牢固;②农民拉绳插秧;
③解放军叔叔打靶瞄准;④从A地到B地架设电线,总是尽可
能沿着线段AB架设.
A.1 B.2 C.3 D.4
C
点拨:
①②③现象可以用两点确定一条直线来解释;④现象可以用两点之间,线段最短来解释.
小试牛刀
6.下列现象中,可用基本事实“两点之间,线段最短”来解释的是( )
A.用两个钉子就可以把木条固定在墙上
B.把弯曲的公路改直,就能缩短路程
C.利用圆规可以比较两条线段的长短关系
D.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
B
小试牛刀
7.如图所示的图形中哪些图形是立体图形,哪些图形是平面图形?
解:
立体图形有:①④⑤⑥⑦
平面图形有:②③⑧
小试牛刀
8.如图,已知线段AD=10 cm,点B,C都是线段AD上的点,且AC=7 cm,BD=4 cm. 若点E,F分别是线段AB,CD的中点,求线段EF的长.
解:
因为点E,F分别是线段AB,CD的中点,
所以EF=BE+BC+CF= AB+BC+ CD
= AB+ CD+ BC+ BC
= (AB+BC+CD+BC)
= (AC+BD) = ×(7+4)= (cm).
小试牛刀
9.如图,已知AB和CD的公共部分BD= AB= CD,线段AB,CD的中点E,F之间的距离是10 cm,求AB,CD的长.
解:
因为BD= AB= CD,所以CD= AB.
因为F是CD的中点,
所以DF= CD= × AB= AB.
小试牛刀
因为E是AB的中点,所以EB= AB,
所以ED=EB-DB= AB- AB= AB.
所以EF=ED+DF= AB+ AB
= AB=10 cm,
所以AB=12 cm,
所以CD= AB=16 cm.
课堂小结
课堂小结
点、线、面、体及它们之间的关系.
点 线 面 体
点动成线
面动成体
线动成面
线与线相交形成点
面与面相交形成线
包围着体的部分是面
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
