人教版(新)七上-4.3.3 余角和补角 第一课时【优质课件】
文档属性
| 名称 | 人教版(新)七上-4.3.3 余角和补角 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
4.3.3 余角和补角
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
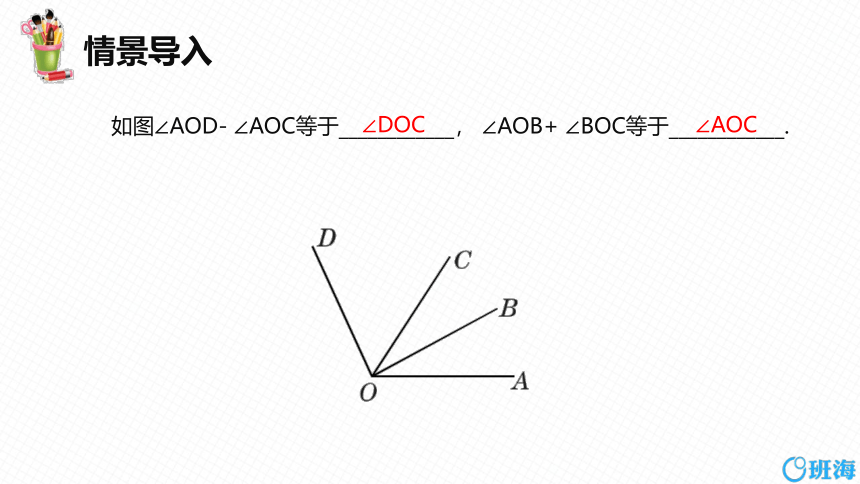
情景导入
如图∠AOD- ∠AOC等于____________, ∠AOB+ ∠BOC等于____________.
∠DOC
∠AOC
新课精讲
探索新知
1
知识点
余角和补角
如果两个角的和等于90 (直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
如果两个角的和等于180 (平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
探索新知
探究1(1)在一副三角板中,每块都有一个角是90°,那么其余两
个角的和是多少?
(2)已知∠1=36°,∠2=54°,那么∠1+∠2=?
探究2(1)观察如图所示的两个角,你能猜想∠1+∠2等于多少度?
(2)如果∠1=144°,∠2=36°,那么∠1+∠2=?
探索新知
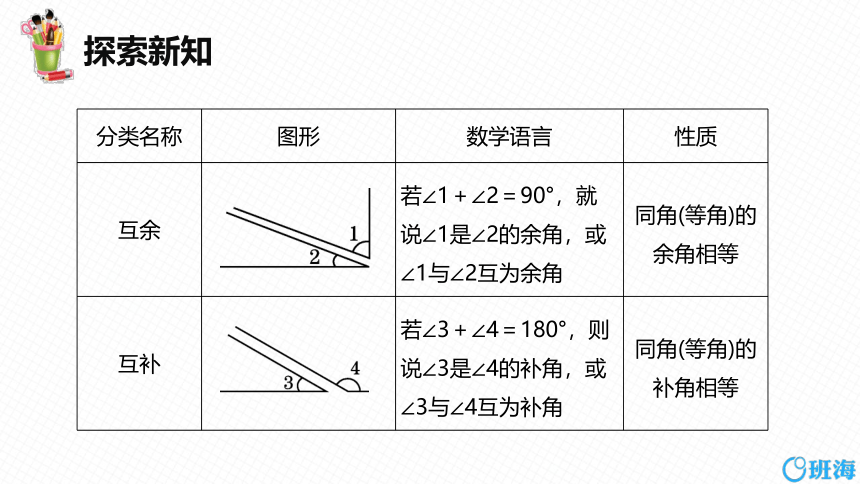
分类名称 图形 数学语言 性质
互余 若∠1+∠2=90°,就说∠1是∠2的余角,或∠1与∠2互为余角 同角(等角)的余角相等
互补 若∠3+∠4=180°,则说∠3是∠4的补角,或∠3与∠4互为补角 同角(等角)的补角相等
探索新知
要点精析:
(1)互余,互补必须是两个角之间的关系.
(2)当互补的两个角有公共顶点和公共边时,又称这两个角互为邻补角(简称邻补角).如图所示,∠AOC和∠BOC互为邻补角.
(3)互补的角不一定互为邻补角,但互为邻补角的角一定互为补角.
(4)互余或互补的角只与数量有关,与位置无关.
探索新知
例1 下列说法正确的有 ( )
①锐角的余角是锐角,锐角的补角是锐角;
②直角没有补角;
③钝角没有余角,钝角的补角是锐角;
④直角的补角还是直角;
⑤一个角的补角与它的余角的差为90°;
⑥两个角相等,它们的补角也相等.
A.3个 B.4个 C.5个 D.6个
导引:主要紧扣锐角、钝角、余角、补角的特征进行判断,除①②不正
确外,其他说法都正确.
B
探索新知
总 结
由于互余的两个角之和为90°,所以这两个角都为锐角;互补的两个角之和为180°,所以这两个角为一个锐角一个钝角或两个角都为直角.
探索新知
例2 如图,点A,O, B在同一条直线 上,射线OD和
射线OE分别平分∠AOC和∠BOC, 图中哪些角互
为余角?
解:因为点A,O, B在同一条直线上,所以 ∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC和∠BOC,
所以∠COD+∠COE= ∠AOC+ ∠BOC= (∠AOC+∠BOC)= 90°.
所以,∠COD和∠COE互为余角,
同理,∠AOD和∠BOE,∠AOD和∠COE,∠COD 和∠BOE也互为余角.
典题精讲
1.已知∠α=35°,那么∠α的余角等于( )
A.35° B.55°
C.65° D.145°
2.已知∠α=35°,那么∠α的补角的度数是( )
A.55° B.65°
C.145° D.165°
B
C
典题精讲
3.下列说法正确的是( )
A.两个锐角一定互余
B.锐角和钝角一定互补
C.互余且相等的两角一定是45°
D.同一角的余角与它的补角一定相等
C
探索新知
2
知识点
余角和补角的有关计算
例3 如图,∠AOB与∠AOD分别是∠AOC的余角和补角,且OC是
∠BOD的平分线,求∠AOC和∠BOD.
导引:此题中角的关系错综复杂,
适宜用方程去解决.
探索新知
解:设∠AOC=x°. 则∠AOB=(90-x)°,∠AOD=(180-x)°.
因为∠BOC=∠AOC-∠AOB,
所以∠BOC=[x-(90-x)]°=(2x-90)°.
因为∠COD=∠AOD-∠AOC,
所以∠COD=[(180-x)-x]°=(180-2x)°.
因为OC平分∠BOD,所以∠BOC=∠COD.
所以2x-90=180-2x. 解得x=67.5.
所以∠AOC=67.5°,
∠BOD=∠AOD-∠AOB =(180°-67.5°)-(90°-67.5°)=90°.
探索新知
总 结
(1)用方程解几何题,本节中已多次出现.这是方程思想的应用.
(2)图中∠BOD是同一个角的补角与余角的差,所以∠BOD=90°,
与锐角∠AOC的大小无关.
(3)方程中一般不出现单位.
典题精讲
1.一个角比它的余角大10°,这个角为( )
A.40° B.45° C.50° D.55°
2.如图,直线AB与CD相交于O点,∠EOB=90°,则图中∠1与∠2的
关系是( )
A.互补 B.互余
C.相等 D.无法确定
C
C
典题精讲
3.一个角的补角比它的余角( )
A.相等
B.小90°
C.大90°
D.不确定大小
C
学以致用
小试牛刀
1.下列说法中正确的有_____________.(填序号)
①钝角与锐角互补;
②∠α的余角90°-∠α;
③∠β的补交是180°- ∠β ;
④若∠1+ ∠2+ ∠3=90°,则∠1, ∠2, ∠3互余。
②③
2.已知∠α=35°,则∠α的余角的度数是( )
A.55° B.45°
C.55° D.45°
A
小试牛刀
3.已知∠α=35°,则∠α的余角的度数是( )
A.55° B.45°
C.55° D.45°
A
4.下列各图中,∠1与∠2互为余角的是( )
A. B. C. D.
B
小试牛刀
5.下面角的图示中,能与30°角互补的是( )
A. B. C. D.
D
6.已知M、N、P、Q四点的位置如图所示,下列结论中,正确的是( )
A. ∠NOQ=42°
B. ∠NOP=132°
C. ∠PON比∠MOQ大
D. ∠MOQ与∠MOP互补
C
小试牛刀
7.如图,直线AB与CD相交于点O,∠EOB=90°,∠FOD=90°,如果
∠AOD=140°,那么∠EOF=( )
A. 30° B. 40°
C.50° D. 60°
B
解析:由题意知,∠EOB=∠FOD=90°,
∴∠AOE=∠FOC=90°, ∵∠AOD=140°,
∴∠EOD=∠AOD-∠AOE=140°-90°=50°,
∴∠EOF=∠FOD-∠EOD=90°-50°=40°.
故选B.
小试牛刀
8.如图,再三角形ABC中,∠C=90°,点D,E分别在AC,AB上.若∠B=
∠ADE,则下列结论正确的是( )
A. ∠A和∠B互为补角
B. ∠B和∠ADE,互为补角
C. ∠A和∠ADE互为余角
D. ∠AED和∠DEB互为余角
C
小试牛刀
9.如图,O是直线AB上一点,OC为任一条射线,
OD平分∠BOC, OE平分∠AOC。
(1)指出图中∠AOD与∠BOE的补角;
(2)试说明∠COD与∠COE具有怎样的数量关系.
解:与∠AOD互补的角∠BOD、∠COD; 与∠BOE互补的角∠AOE、∠COE
解:因为OD平分∠BOC,所以∠COD=∠BOC。
又因为OE平分∠AOC,所以∠COE=∠AOC,
所以∠COD+∠COE=∠BOC+∠AOC=(∠BOC+∠AOC),
所以∠COD+∠COE=∠AOB=90°
课堂小结
课堂小结
互余的角 互补的角
数量关系
对应图形
性质
1+ 2=90°
C
D
E
N
A
O
B
M
1+ 2=180°
同角(等角)的余角相等
同角(等角)的补角相等
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
4.3.3 余角和补角
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图∠AOD- ∠AOC等于____________, ∠AOB+ ∠BOC等于____________.
∠DOC
∠AOC
新课精讲
探索新知
1
知识点
余角和补角
如果两个角的和等于90 (直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
如果两个角的和等于180 (平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
探索新知
探究1(1)在一副三角板中,每块都有一个角是90°,那么其余两
个角的和是多少?
(2)已知∠1=36°,∠2=54°,那么∠1+∠2=?
探究2(1)观察如图所示的两个角,你能猜想∠1+∠2等于多少度?
(2)如果∠1=144°,∠2=36°,那么∠1+∠2=?
探索新知
分类名称 图形 数学语言 性质
互余 若∠1+∠2=90°,就说∠1是∠2的余角,或∠1与∠2互为余角 同角(等角)的余角相等
互补 若∠3+∠4=180°,则说∠3是∠4的补角,或∠3与∠4互为补角 同角(等角)的补角相等
探索新知
要点精析:
(1)互余,互补必须是两个角之间的关系.
(2)当互补的两个角有公共顶点和公共边时,又称这两个角互为邻补角(简称邻补角).如图所示,∠AOC和∠BOC互为邻补角.
(3)互补的角不一定互为邻补角,但互为邻补角的角一定互为补角.
(4)互余或互补的角只与数量有关,与位置无关.
探索新知
例1 下列说法正确的有 ( )
①锐角的余角是锐角,锐角的补角是锐角;
②直角没有补角;
③钝角没有余角,钝角的补角是锐角;
④直角的补角还是直角;
⑤一个角的补角与它的余角的差为90°;
⑥两个角相等,它们的补角也相等.
A.3个 B.4个 C.5个 D.6个
导引:主要紧扣锐角、钝角、余角、补角的特征进行判断,除①②不正
确外,其他说法都正确.
B
探索新知
总 结
由于互余的两个角之和为90°,所以这两个角都为锐角;互补的两个角之和为180°,所以这两个角为一个锐角一个钝角或两个角都为直角.
探索新知
例2 如图,点A,O, B在同一条直线 上,射线OD和
射线OE分别平分∠AOC和∠BOC, 图中哪些角互
为余角?
解:因为点A,O, B在同一条直线上,所以 ∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC和∠BOC,
所以∠COD+∠COE= ∠AOC+ ∠BOC= (∠AOC+∠BOC)= 90°.
所以,∠COD和∠COE互为余角,
同理,∠AOD和∠BOE,∠AOD和∠COE,∠COD 和∠BOE也互为余角.
典题精讲
1.已知∠α=35°,那么∠α的余角等于( )
A.35° B.55°
C.65° D.145°
2.已知∠α=35°,那么∠α的补角的度数是( )
A.55° B.65°
C.145° D.165°
B
C
典题精讲
3.下列说法正确的是( )
A.两个锐角一定互余
B.锐角和钝角一定互补
C.互余且相等的两角一定是45°
D.同一角的余角与它的补角一定相等
C
探索新知
2
知识点
余角和补角的有关计算
例3 如图,∠AOB与∠AOD分别是∠AOC的余角和补角,且OC是
∠BOD的平分线,求∠AOC和∠BOD.
导引:此题中角的关系错综复杂,
适宜用方程去解决.
探索新知
解:设∠AOC=x°. 则∠AOB=(90-x)°,∠AOD=(180-x)°.
因为∠BOC=∠AOC-∠AOB,
所以∠BOC=[x-(90-x)]°=(2x-90)°.
因为∠COD=∠AOD-∠AOC,
所以∠COD=[(180-x)-x]°=(180-2x)°.
因为OC平分∠BOD,所以∠BOC=∠COD.
所以2x-90=180-2x. 解得x=67.5.
所以∠AOC=67.5°,
∠BOD=∠AOD-∠AOB =(180°-67.5°)-(90°-67.5°)=90°.
探索新知
总 结
(1)用方程解几何题,本节中已多次出现.这是方程思想的应用.
(2)图中∠BOD是同一个角的补角与余角的差,所以∠BOD=90°,
与锐角∠AOC的大小无关.
(3)方程中一般不出现单位.
典题精讲
1.一个角比它的余角大10°,这个角为( )
A.40° B.45° C.50° D.55°
2.如图,直线AB与CD相交于O点,∠EOB=90°,则图中∠1与∠2的
关系是( )
A.互补 B.互余
C.相等 D.无法确定
C
C
典题精讲
3.一个角的补角比它的余角( )
A.相等
B.小90°
C.大90°
D.不确定大小
C
学以致用
小试牛刀
1.下列说法中正确的有_____________.(填序号)
①钝角与锐角互补;
②∠α的余角90°-∠α;
③∠β的补交是180°- ∠β ;
④若∠1+ ∠2+ ∠3=90°,则∠1, ∠2, ∠3互余。
②③
2.已知∠α=35°,则∠α的余角的度数是( )
A.55° B.45°
C.55° D.45°
A
小试牛刀
3.已知∠α=35°,则∠α的余角的度数是( )
A.55° B.45°
C.55° D.45°
A
4.下列各图中,∠1与∠2互为余角的是( )
A. B. C. D.
B
小试牛刀
5.下面角的图示中,能与30°角互补的是( )
A. B. C. D.
D
6.已知M、N、P、Q四点的位置如图所示,下列结论中,正确的是( )
A. ∠NOQ=42°
B. ∠NOP=132°
C. ∠PON比∠MOQ大
D. ∠MOQ与∠MOP互补
C
小试牛刀
7.如图,直线AB与CD相交于点O,∠EOB=90°,∠FOD=90°,如果
∠AOD=140°,那么∠EOF=( )
A. 30° B. 40°
C.50° D. 60°
B
解析:由题意知,∠EOB=∠FOD=90°,
∴∠AOE=∠FOC=90°, ∵∠AOD=140°,
∴∠EOD=∠AOD-∠AOE=140°-90°=50°,
∴∠EOF=∠FOD-∠EOD=90°-50°=40°.
故选B.
小试牛刀
8.如图,再三角形ABC中,∠C=90°,点D,E分别在AC,AB上.若∠B=
∠ADE,则下列结论正确的是( )
A. ∠A和∠B互为补角
B. ∠B和∠ADE,互为补角
C. ∠A和∠ADE互为余角
D. ∠AED和∠DEB互为余角
C
小试牛刀
9.如图,O是直线AB上一点,OC为任一条射线,
OD平分∠BOC, OE平分∠AOC。
(1)指出图中∠AOD与∠BOE的补角;
(2)试说明∠COD与∠COE具有怎样的数量关系.
解:与∠AOD互补的角∠BOD、∠COD; 与∠BOE互补的角∠AOE、∠COE
解:因为OD平分∠BOC,所以∠COD=∠BOC。
又因为OE平分∠AOC,所以∠COE=∠AOC,
所以∠COD+∠COE=∠BOC+∠AOC=(∠BOC+∠AOC),
所以∠COD+∠COE=∠AOB=90°
课堂小结
课堂小结
互余的角 互补的角
数量关系
对应图形
性质
1+ 2=90°
C
D
E
N
A
O
B
M
1+ 2=180°
同角(等角)的余角相等
同角(等角)的补角相等
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
