人教版(新)七上-1.2.3 相反数【优质课件】
文档属性
| 名称 | 人教版(新)七上-1.2.3 相反数【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览











文档简介
(共36张PPT)
1.2.3 相反数
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
探究:
在数轴上,与原点的距离是2的点有几个?这些点各
表示哪个数?
设a是一个正数. 数轴上与原点的距离等于a的点有几
个?这些点表示的数有什么关系?
新课精讲
探索新知
1
知识点
相反数的定义
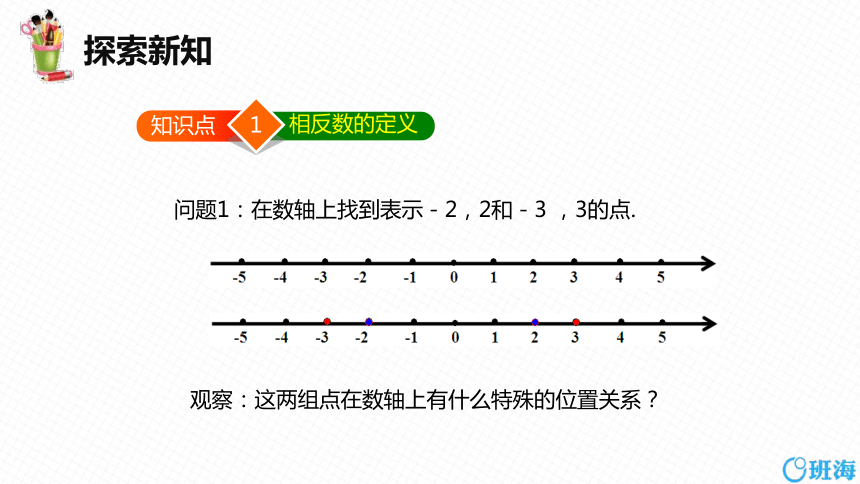
问题1:在数轴上找到表示-2,2和-3 ,3的点.
观察:这两组点在数轴上有什么特殊的位置关系?
探索新知
结论:表示每组中两个数的点都位于原点的两旁,
且与原点的距离相等.
思考:你还能举出数轴上其它点的例子吗?
探索新知
问题2:观察数轴,说出在数轴上与原点的距离是 2
的点有几个?这些点各表示哪些数?设a是一个正数,
数轴上与原点的距离等于a的点有几个?这些点表示
的数有什么关系?
探索新知
数轴上与原点的距离是 2的点有两个,表示为-2和2;如果a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右,表示为-a和a,我们说这两个点关于原点对称.
归 纳
探索新知
只有符号不同的两个数叫做互为相反数. 特别地,
0的相反数是0.
定义:
问题3:你能再举出几组互为相反数的数的例子吗?
探索新知
相反数的代数意义:只有符号不同的两个数叫做
互为相反数.特殊规定:0的相反数是0.
2. 相反数的求法:求一个数的相反数就是在这个数
的前面加上“-”号,即a的相反数是-a,其实
质是改变这个数的符号.
探索新知
例1 下列说法正确的是( )
A.-2是相反数
B. 与-2互为相反数
C.-3与+2互为相反数
D. 与0.5互为相反数
D
导引:判断两个数是否互为相反数,按其定义从两方面去看:
符号(+、-)和所含数字(相同).
探索新知
总 结
(1)相反数不能单独存在,前提是“互为”;
(2)判断两个数是否互为相反数,要从两个方面看,
一是符号不能相同;
二是数字一定要相同.
探索新知
例2 分别写出下列各数的相反数.
-3,2,4.5,0,- .
导引:根据相反数的代数意义(只有符号不同的两个数互为相
反数),直接写出一个数的相反数.
解:-3的相反数是3,2的相反数是-2,4.5的相反数是
-4.5,0的相反数是0,
探索新知
总 结
(1)在一个省略正号的正数的前面添加负号,即可
得到这个数的相反数;(2)直接去掉负数的负号即可得
到它的相反数,0的相反数是0,任何有理数有且只有
一个相反数.
典题精讲
1.-15的相反数是( )
A.15 B.-15 C.±15 D.
2.一个数的相反数是3,这个数是( )
A. B.- C.3 D.-3
A
D
3.在2,-2,6,8这四个数中,互为相反数的是( )
A.-2与2 B.2与8
C.-2与6 D.6与8
A
典题精讲
4.如图,表示互为相反数的两个数的点是________.
B C
5.判断下列说法是否正确:
(1)-3是相反数 ;
(2)+3是相反数;
(3)3是-3的相反数;
(4)-3与+3互为相反数.
×
×
√
√
探索新知
2
知识点
多重符号的化简
例4 化简下列各数:
(1)-[+(-1)];(2)-{-[-…(-1) …]}.
(2n-1)个负号,n为正整数
导引:(1)-[+(-1)]表示+(-1)的相反数,即-1的相反数;
(2)2n-1为奇数,所以结果为负数.
解: (1)1; (2)-1.
探索新知
总 结
化简一个带有多重符号的数,与它前面的“+”号个数无关,与“-”号个数有关,当“-”号的个数为奇数时,这个数为负,当“-”号的个数为偶数时,这个数为正;即我们可以按照“奇负偶正”的原则直接写出结果.
典题精讲
2.化简下列各数:
-(-68) : -(+0.75):
-(+3.8):
1.如果a=- a,那么表示a 的点在数轴上的什么位置?
原点
68
-0.75
-3.8
典题精讲
4.化简下列各数:
(1)-[-(+2)]=______;
(2)-[-(-2 017)]=________;
(3)-[+(-18)]=__________;
(4) ___________.
3.a的相反数是-(+5),则a=________.
5
2
-2017
18
探索新知
3
知识点
相反数的性质
-2.5与+2.5,+1与-1,+3与-3
0
.
.
+2.5
-2.5
0
.
.
+1
-1
每一对数在数轴上的对应点位于原点的两侧,且到原点的距离相等.
探索新知
-7表示__的相反数;
-(-7) 表示___的相反数.
在一个数的前面添上“-”号表示原来这个数的相反数.
在一个数的前面添上“+”号表示这个数本身.
7
-7
-7的相反数是7
探索新知
(1) 的相反数为________; (2)2是______的相反数;
(3)x-y的相反数为_________; (4)π-3的相反数是__________.
例3 填空:
-(x-y)
-(π-3)
(2)在2的前面添上“-”号即可得到它的相反数-2;
(3)将x-y括起来,前面添上“-”号即可得到它的相反数-(x-y);
(4)将π-3括起来,前面添上“-”号即可得到它的相反数-(π-3).
探索新知
总 结
求一个数的相反数,只要在这个数的前面添上“-”号,即可得到这个数的相反数.
典题精讲
1.下列说法:其中正确的个数是( )
①m与-m互为相反数,因此它们一定不相等;
②相反数等于它本身的数只有0; ③正数和负数互为相反数;
④负数的相反数是正数; ⑤a的相反数一定是负数.
A.1 B.2 C.3 D.4
B
学以致用
小试牛刀
1.只有________不同的两个数叫做互为相反数.相反数具有以下
4个特征:
(1)相反数是________出现的;
(2)定义中“只有”指的是除______不同外,其他完全______;
(3)0的相反数是0;
(4)在数轴上,表示互为相反数的两个点位于原点的两侧,且到
原点的距离________.
符号
成对
符号
相同
相等
小试牛刀
2.运用相反数的意义化简多重符号,若数字前面的负号有偶
数个,则结果为____数;若数字前面的负号有____数个,
则结果为负数.
正
奇
3.若数a是一个正数,则它的相反数是一个______数;若数a的相反数是一个正数,则数a是一个____数.
负
负
小试牛刀
4.如图,已知A,B,C,D四个点在一条没有标明原点的数轴上.
(1)若点A和点C表示的数互为相反数,则原点为________;
点B
(2)若点B和点D表示的数互为相反数,则原点为________;
(3)若点A和点D表示的数互为相反数,请在数轴上标出原点O的位置.
点C
解:如图所示.
小试牛刀
5.中国人最早使用负数,可追溯到两千多年前的秦汉时期.
-0.5的相反数是( )
A.0.5 B.±0.5 C.-0.5 D.5
A
6.下列各组数中,不相等的是( )
A.-(+2)和+(-2) B.-7和-(+7)
C.+(-5)和-(-5) D.-[+(-1)]和-[-(+1)]
C
小试牛刀
7.如图,数轴上两点A,B表示的数互为相反数,则点B表示
的数为( )
A.-6 B.6 C.0 D.无法确定
B
8.如图,数轴上表示数-2的相反数的点是( )
A.点P B.点Q C.点M D.点N
A
小试牛刀
9.如图是一个正方体纸盒的平面展开图.若在其中三个正方形
A,B,C内分别填入适当的数,使得折成正方体后相对面上
的两个数互为相反数,则填入正方形A,B,
C内的数分别是多少?
【思路点拨】
可在纸片上画出如图所示的平面展开图后剪下,折叠成正方体后即可求出.
解: 与A相对的面上的数是-1,所以填入正方形A内的数为1;与B相对的面上的数是2,所以填入正方形B内的数为-2;与C相对的面上的数是0,所以填入正方形C内的数为0.
课堂小结
课堂小结
1.相反数的意义:
代数意义:(1)成对出现;(2)只有符号不同,即a的相反数
是-a,特殊地:0的相反数是0.
几何意义:数轴上原点两旁且到原点距离相等的两个点所
表示的数互为相反数.
2.多重符号化简的方法规律:
方法一:把所有的正号去掉;负号的个数是偶数个时结果为
正,是奇数个时结果为负,即“奇负偶正”.
方法二:采用两个同号得正,异号得负,分层化简.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.2.3 相反数
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
探究:
在数轴上,与原点的距离是2的点有几个?这些点各
表示哪个数?
设a是一个正数. 数轴上与原点的距离等于a的点有几
个?这些点表示的数有什么关系?
新课精讲
探索新知
1
知识点
相反数的定义
问题1:在数轴上找到表示-2,2和-3 ,3的点.
观察:这两组点在数轴上有什么特殊的位置关系?
探索新知
结论:表示每组中两个数的点都位于原点的两旁,
且与原点的距离相等.
思考:你还能举出数轴上其它点的例子吗?
探索新知
问题2:观察数轴,说出在数轴上与原点的距离是 2
的点有几个?这些点各表示哪些数?设a是一个正数,
数轴上与原点的距离等于a的点有几个?这些点表示
的数有什么关系?
探索新知
数轴上与原点的距离是 2的点有两个,表示为-2和2;如果a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右,表示为-a和a,我们说这两个点关于原点对称.
归 纳
探索新知
只有符号不同的两个数叫做互为相反数. 特别地,
0的相反数是0.
定义:
问题3:你能再举出几组互为相反数的数的例子吗?
探索新知
相反数的代数意义:只有符号不同的两个数叫做
互为相反数.特殊规定:0的相反数是0.
2. 相反数的求法:求一个数的相反数就是在这个数
的前面加上“-”号,即a的相反数是-a,其实
质是改变这个数的符号.
探索新知
例1 下列说法正确的是( )
A.-2是相反数
B. 与-2互为相反数
C.-3与+2互为相反数
D. 与0.5互为相反数
D
导引:判断两个数是否互为相反数,按其定义从两方面去看:
符号(+、-)和所含数字(相同).
探索新知
总 结
(1)相反数不能单独存在,前提是“互为”;
(2)判断两个数是否互为相反数,要从两个方面看,
一是符号不能相同;
二是数字一定要相同.
探索新知
例2 分别写出下列各数的相反数.
-3,2,4.5,0,- .
导引:根据相反数的代数意义(只有符号不同的两个数互为相
反数),直接写出一个数的相反数.
解:-3的相反数是3,2的相反数是-2,4.5的相反数是
-4.5,0的相反数是0,
探索新知
总 结
(1)在一个省略正号的正数的前面添加负号,即可
得到这个数的相反数;(2)直接去掉负数的负号即可得
到它的相反数,0的相反数是0,任何有理数有且只有
一个相反数.
典题精讲
1.-15的相反数是( )
A.15 B.-15 C.±15 D.
2.一个数的相反数是3,这个数是( )
A. B.- C.3 D.-3
A
D
3.在2,-2,6,8这四个数中,互为相反数的是( )
A.-2与2 B.2与8
C.-2与6 D.6与8
A
典题精讲
4.如图,表示互为相反数的两个数的点是________.
B C
5.判断下列说法是否正确:
(1)-3是相反数 ;
(2)+3是相反数;
(3)3是-3的相反数;
(4)-3与+3互为相反数.
×
×
√
√
探索新知
2
知识点
多重符号的化简
例4 化简下列各数:
(1)-[+(-1)];(2)-{-[-…(-1) …]}.
(2n-1)个负号,n为正整数
导引:(1)-[+(-1)]表示+(-1)的相反数,即-1的相反数;
(2)2n-1为奇数,所以结果为负数.
解: (1)1; (2)-1.
探索新知
总 结
化简一个带有多重符号的数,与它前面的“+”号个数无关,与“-”号个数有关,当“-”号的个数为奇数时,这个数为负,当“-”号的个数为偶数时,这个数为正;即我们可以按照“奇负偶正”的原则直接写出结果.
典题精讲
2.化简下列各数:
-(-68) : -(+0.75):
-(+3.8):
1.如果a=- a,那么表示a 的点在数轴上的什么位置?
原点
68
-0.75
-3.8
典题精讲
4.化简下列各数:
(1)-[-(+2)]=______;
(2)-[-(-2 017)]=________;
(3)-[+(-18)]=__________;
(4) ___________.
3.a的相反数是-(+5),则a=________.
5
2
-2017
18
探索新知
3
知识点
相反数的性质
-2.5与+2.5,+1与-1,+3与-3
0
.
.
+2.5
-2.5
0
.
.
+1
-1
每一对数在数轴上的对应点位于原点的两侧,且到原点的距离相等.
探索新知
-7表示__的相反数;
-(-7) 表示___的相反数.
在一个数的前面添上“-”号表示原来这个数的相反数.
在一个数的前面添上“+”号表示这个数本身.
7
-7
-7的相反数是7
探索新知
(1) 的相反数为________; (2)2是______的相反数;
(3)x-y的相反数为_________; (4)π-3的相反数是__________.
例3 填空:
-(x-y)
-(π-3)
(2)在2的前面添上“-”号即可得到它的相反数-2;
(3)将x-y括起来,前面添上“-”号即可得到它的相反数-(x-y);
(4)将π-3括起来,前面添上“-”号即可得到它的相反数-(π-3).
探索新知
总 结
求一个数的相反数,只要在这个数的前面添上“-”号,即可得到这个数的相反数.
典题精讲
1.下列说法:其中正确的个数是( )
①m与-m互为相反数,因此它们一定不相等;
②相反数等于它本身的数只有0; ③正数和负数互为相反数;
④负数的相反数是正数; ⑤a的相反数一定是负数.
A.1 B.2 C.3 D.4
B
学以致用
小试牛刀
1.只有________不同的两个数叫做互为相反数.相反数具有以下
4个特征:
(1)相反数是________出现的;
(2)定义中“只有”指的是除______不同外,其他完全______;
(3)0的相反数是0;
(4)在数轴上,表示互为相反数的两个点位于原点的两侧,且到
原点的距离________.
符号
成对
符号
相同
相等
小试牛刀
2.运用相反数的意义化简多重符号,若数字前面的负号有偶
数个,则结果为____数;若数字前面的负号有____数个,
则结果为负数.
正
奇
3.若数a是一个正数,则它的相反数是一个______数;若数a的相反数是一个正数,则数a是一个____数.
负
负
小试牛刀
4.如图,已知A,B,C,D四个点在一条没有标明原点的数轴上.
(1)若点A和点C表示的数互为相反数,则原点为________;
点B
(2)若点B和点D表示的数互为相反数,则原点为________;
(3)若点A和点D表示的数互为相反数,请在数轴上标出原点O的位置.
点C
解:如图所示.
小试牛刀
5.中国人最早使用负数,可追溯到两千多年前的秦汉时期.
-0.5的相反数是( )
A.0.5 B.±0.5 C.-0.5 D.5
A
6.下列各组数中,不相等的是( )
A.-(+2)和+(-2) B.-7和-(+7)
C.+(-5)和-(-5) D.-[+(-1)]和-[-(+1)]
C
小试牛刀
7.如图,数轴上两点A,B表示的数互为相反数,则点B表示
的数为( )
A.-6 B.6 C.0 D.无法确定
B
8.如图,数轴上表示数-2的相反数的点是( )
A.点P B.点Q C.点M D.点N
A
小试牛刀
9.如图是一个正方体纸盒的平面展开图.若在其中三个正方形
A,B,C内分别填入适当的数,使得折成正方体后相对面上
的两个数互为相反数,则填入正方形A,B,
C内的数分别是多少?
【思路点拨】
可在纸片上画出如图所示的平面展开图后剪下,折叠成正方体后即可求出.
解: 与A相对的面上的数是-1,所以填入正方形A内的数为1;与B相对的面上的数是2,所以填入正方形B内的数为-2;与C相对的面上的数是0,所以填入正方形C内的数为0.
课堂小结
课堂小结
1.相反数的意义:
代数意义:(1)成对出现;(2)只有符号不同,即a的相反数
是-a,特殊地:0的相反数是0.
几何意义:数轴上原点两旁且到原点距离相等的两个点所
表示的数互为相反数.
2.多重符号化简的方法规律:
方法一:把所有的正号去掉;负号的个数是偶数个时结果为
正,是奇数个时结果为负,即“奇负偶正”.
方法二:采用两个同号得正,异号得负,分层化简.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
