人教版(新)七上-1.4.1 有理数的乘法 第二课时【优质课件】
文档属性
| 名称 | 人教版(新)七上-1.4.1 有理数的乘法 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 14:27:48 | ||
图片预览









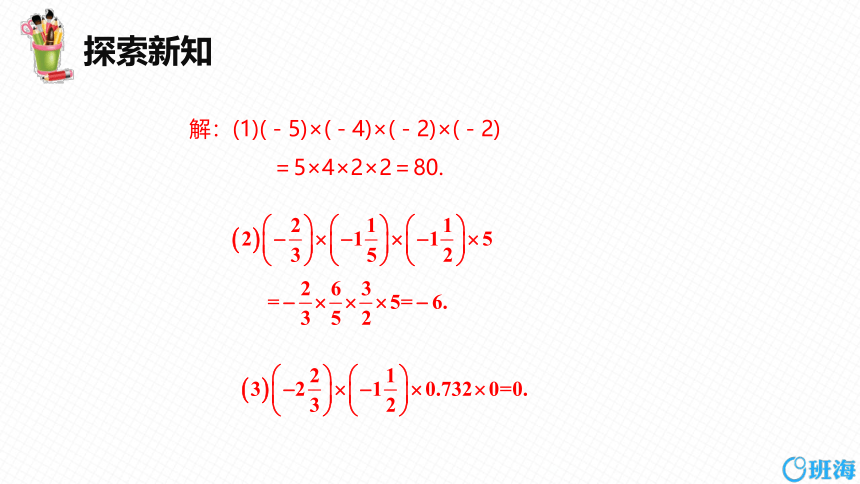


文档简介
(共35张PPT)
1.4.1 有理数的乘法
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘. 任何数与0相乘,积仍为0.
2. 几个不等于零的数相乘,积的符号由负因数的个数决定:
(1)当负因数的个数是偶数时,积是正数;
(2)当负因数的个数是奇数时,积是负数.
3. 几个数相乘,如果其中有因数为0,积等于0.
复习回顾:
新课精讲
探索新知
1
知识点
多个有理数相乘
思考:
你能看出下式的结果吗?如果能,请说明理由.
7.8×(-8.1) ×0 ×(-19.6).
几个数相乘,如果其中有因数为0,积等于____.
0
探索新知
要点精析:
(1)在有理数乘法中,每个乘数都叫做一个因数.
(2)几个不为0的有理数相乘,先确定积的符号,然后将绝对值相乘.
(3)几个有理数相乘,如果有一个因数为0,那么积就等于0;反之,如果积为0,那么至少有一个因数为0.
探索新知
例1 计算:
多个不是0的数相乘,先做哪一步,再做哪一步?
探索新知
例2 计算:(1)(-5)×(-4)×(-2)×(-2);
(2)
(3)
导引:(1)负因数的个数为偶数,结果为正数.(2)负因数的
个数为奇数,结果为负数.(3)几个数相乘,如果其
中有因数为0,那么积等于0.
探索新知
解:(1)(-5)×(-4)×(-2)×(-2)
=5×4×2×2=80.
探索新知
总 结
多个有理数相乘时,先定积的符号,再定积的绝对值,在运算时,一般情况下先把式子中所有的小数化为分数、带分数化为假分数之后再计算.
典题精讲
2.下列各式中积为负数的是( )
A.(-2)×(-2)×(-2)×2 B.(-2)×3×4×(-2)
C.(-4)×5×(-3)×8 D.(-5)×(-7)×(-9)×(-1)
A
1.n个不等于零的有理数相乘,它们的积的符号( )
A.由因数的个数决定 B.由正因数的个数决定
C.由负因数的个数决定 D.由负因数的大小决定
C
典题精讲
3.若五个有理数相乘的积为正数,则五个数中负数的个数是( )
A.0 B.2 C.4 D.0或2或4
4.有2 016个有理数相乘,如果积为0,那么在2 016个有理数中( )
A.全部为0 B.只有一个因数为0
C.至少有一个为0 D.有两个数互为相反数
D
C
探索新知
2
知识点
有理数的乘法运算律
问题1: 计算下列各题,并比较它们的结果,你有什么发现?请再举几个例子验证你的发现.
5× (-6) (-6) ×5
= -30
= -30
两个数相乘,交换因数的位置,积不变
乘法交换律:ab=ba
探索新知
问题2: 计算下列各题,并比较它们的结果,你有什么发现?请再举几个例子验证你的发现.
[3×(-4)] × (-5) 3 ×[(-4) × (-5)]
= 60
= 60
三个数相乘,先把前两个数相乘,或者先把
后两个数相乘,积不变.
乘法结合律:(ab)c=a(bc)
探索新知
根据乘法交换律和结合律可以推出:
三个以上有理数相乘,可以任意交换因数的位置,也可先把其中的几个数相乘.
探索新知
问题3: 计算下列各题,并比较它们的结果,你有什么发现?请再举几个例子验证你的发现.
= -20
5 ×[3+(-7)] 5 ×3 + 5 ×(-7)
= -20
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
乘法分配律:a(b+c)=ab+ac
探索新知
根据分配律可以推出:
一个数同几个数的和相乘,等于把这个数分别同这几个数相乘,再把积相加.
探索新知
例3 计算:
导引:根据题中数据特征,运用乘法交换律、结
合律进行计算.
探索新知
探索新知
总 结
对于几个有理数相乘,先确定积的符号,再把能够凑整、便于约分的数运用乘法的交换律与结合律结合在一起,进行简便计算.
探索新知
例4 用两种方法计算
解法1:
解法2:
比较两种解法哪个更简便?
探索新知
总 结
题中的12是括号内各分母的公倍数,所以可以利用乘法分配律先去括号,再进行运算.
典题精讲
1.在计算 ×(-36)时,可以避免通分的运算律是( )
A.加法交换律 B.乘法分配律
C.乘法交换律 D.加法结合律
B
2.(-0.125)×15×(-8)× =[(-0.125)× (-8)]× ,
运算中没有运用的运算律是( )
A.乘法交换律 B.乘法结合律
C.分配律 D.乘法交换律和乘法结合律
C
典题精讲
3.下列变形不正确的是( )
A . 5×(-6)=(-6)×5
B. ×(-12)=(-12)×
C. ×(-4)=(-4)× + ×4
D.(-25)×(-16)×(-4)=[(-25)×(-4)]×(-16)
C
典题精讲
4.计算:
=-8500
=25
=15
=-6
学以致用
小试牛刀
1.几个________的数相乘,积的符号由负因数的个数决定,当
负因数的个数为________时,积为______;当负因数的个数
为________时,积为正.
不是0
奇数
负
偶数
2.(1)乘法交换律:一般地,有理数乘法中,两个数相乘,交换
因数的位置,积________,即ab=_____.
(2)乘法结合律:一般地,有理数乘法中,三个数相乘,先把
__________相乘,或者先把___________相乘,积相等,即
(ab)c=__________.
相等
ba
前两个数
后两个数
a(bc)
小试牛刀
(3) 分配律:一般地,有理数乘法中,一个数同两个数的和相
乘,等于把这个数分别同____________相乘,再把________
相加,即a(b+c)=______________.
这两个数
积
ab+ac
3.下列运算过程中,有错误的个数是( )
① ;
②-4×(-7)×(-125)=-(4×125×7);
③ ;
④[3×(-25)]×(-2)=3×[(-25)×(-2)]
A.1 B.2 C.3 D.4
A
小试牛刀
4.三个有理数相乘,积为负数,则其中负因数有( )个.
A.1 B.2 C.3 D.1或3
5.已知a,b,c为非零有理数,下列情况中,它们的积一
定为正数的是( )
A.a,b,c同号 B.a>0,b与c同号
C.b<0,a与c同号 D.a>b>0>c
D
B
小试牛刀
6. =[(-0.125)×(-8)]× ,
运算中运用的运算律是( )
A.乘法交换律 B.乘法结合律
C.分配律 D.乘法交换律和乘法结合律
D
7.已知有理数a,b,c在数轴上的对应点的位置如图所示,
则必有( )
A.abc>0 B.a(b-c)>0
C.(a+b)c>0 D.(a-c)b>0
B
小试牛刀
(1)2×(-1)× (2)
(3)(-1.2)×5×(-3)×(-4)
解:=2×1×
=1
解:
解:=-1.2×5×3×4
=-72.
8.计算:
课堂小结
课堂小结
1、乘法的交换律、结合律只涉及一种运算,而分配律要涉及两种运算.
2、分配律还可写成: ab+ac=a(b+c), 利用它有时也可以简化计算.
3、字母a、b、c可以表示正数、负数,也可以表示零,即a、b、c可以表示任意有理数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.4.1 有理数的乘法
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘. 任何数与0相乘,积仍为0.
2. 几个不等于零的数相乘,积的符号由负因数的个数决定:
(1)当负因数的个数是偶数时,积是正数;
(2)当负因数的个数是奇数时,积是负数.
3. 几个数相乘,如果其中有因数为0,积等于0.
复习回顾:
新课精讲
探索新知
1
知识点
多个有理数相乘
思考:
你能看出下式的结果吗?如果能,请说明理由.
7.8×(-8.1) ×0 ×(-19.6).
几个数相乘,如果其中有因数为0,积等于____.
0
探索新知
要点精析:
(1)在有理数乘法中,每个乘数都叫做一个因数.
(2)几个不为0的有理数相乘,先确定积的符号,然后将绝对值相乘.
(3)几个有理数相乘,如果有一个因数为0,那么积就等于0;反之,如果积为0,那么至少有一个因数为0.
探索新知
例1 计算:
多个不是0的数相乘,先做哪一步,再做哪一步?
探索新知
例2 计算:(1)(-5)×(-4)×(-2)×(-2);
(2)
(3)
导引:(1)负因数的个数为偶数,结果为正数.(2)负因数的
个数为奇数,结果为负数.(3)几个数相乘,如果其
中有因数为0,那么积等于0.
探索新知
解:(1)(-5)×(-4)×(-2)×(-2)
=5×4×2×2=80.
探索新知
总 结
多个有理数相乘时,先定积的符号,再定积的绝对值,在运算时,一般情况下先把式子中所有的小数化为分数、带分数化为假分数之后再计算.
典题精讲
2.下列各式中积为负数的是( )
A.(-2)×(-2)×(-2)×2 B.(-2)×3×4×(-2)
C.(-4)×5×(-3)×8 D.(-5)×(-7)×(-9)×(-1)
A
1.n个不等于零的有理数相乘,它们的积的符号( )
A.由因数的个数决定 B.由正因数的个数决定
C.由负因数的个数决定 D.由负因数的大小决定
C
典题精讲
3.若五个有理数相乘的积为正数,则五个数中负数的个数是( )
A.0 B.2 C.4 D.0或2或4
4.有2 016个有理数相乘,如果积为0,那么在2 016个有理数中( )
A.全部为0 B.只有一个因数为0
C.至少有一个为0 D.有两个数互为相反数
D
C
探索新知
2
知识点
有理数的乘法运算律
问题1: 计算下列各题,并比较它们的结果,你有什么发现?请再举几个例子验证你的发现.
5× (-6) (-6) ×5
= -30
= -30
两个数相乘,交换因数的位置,积不变
乘法交换律:ab=ba
探索新知
问题2: 计算下列各题,并比较它们的结果,你有什么发现?请再举几个例子验证你的发现.
[3×(-4)] × (-5) 3 ×[(-4) × (-5)]
= 60
= 60
三个数相乘,先把前两个数相乘,或者先把
后两个数相乘,积不变.
乘法结合律:(ab)c=a(bc)
探索新知
根据乘法交换律和结合律可以推出:
三个以上有理数相乘,可以任意交换因数的位置,也可先把其中的几个数相乘.
探索新知
问题3: 计算下列各题,并比较它们的结果,你有什么发现?请再举几个例子验证你的发现.
= -20
5 ×[3+(-7)] 5 ×3 + 5 ×(-7)
= -20
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
乘法分配律:a(b+c)=ab+ac
探索新知
根据分配律可以推出:
一个数同几个数的和相乘,等于把这个数分别同这几个数相乘,再把积相加.
探索新知
例3 计算:
导引:根据题中数据特征,运用乘法交换律、结
合律进行计算.
探索新知
探索新知
总 结
对于几个有理数相乘,先确定积的符号,再把能够凑整、便于约分的数运用乘法的交换律与结合律结合在一起,进行简便计算.
探索新知
例4 用两种方法计算
解法1:
解法2:
比较两种解法哪个更简便?
探索新知
总 结
题中的12是括号内各分母的公倍数,所以可以利用乘法分配律先去括号,再进行运算.
典题精讲
1.在计算 ×(-36)时,可以避免通分的运算律是( )
A.加法交换律 B.乘法分配律
C.乘法交换律 D.加法结合律
B
2.(-0.125)×15×(-8)× =[(-0.125)× (-8)]× ,
运算中没有运用的运算律是( )
A.乘法交换律 B.乘法结合律
C.分配律 D.乘法交换律和乘法结合律
C
典题精讲
3.下列变形不正确的是( )
A . 5×(-6)=(-6)×5
B. ×(-12)=(-12)×
C. ×(-4)=(-4)× + ×4
D.(-25)×(-16)×(-4)=[(-25)×(-4)]×(-16)
C
典题精讲
4.计算:
=-8500
=25
=15
=-6
学以致用
小试牛刀
1.几个________的数相乘,积的符号由负因数的个数决定,当
负因数的个数为________时,积为______;当负因数的个数
为________时,积为正.
不是0
奇数
负
偶数
2.(1)乘法交换律:一般地,有理数乘法中,两个数相乘,交换
因数的位置,积________,即ab=_____.
(2)乘法结合律:一般地,有理数乘法中,三个数相乘,先把
__________相乘,或者先把___________相乘,积相等,即
(ab)c=__________.
相等
ba
前两个数
后两个数
a(bc)
小试牛刀
(3) 分配律:一般地,有理数乘法中,一个数同两个数的和相
乘,等于把这个数分别同____________相乘,再把________
相加,即a(b+c)=______________.
这两个数
积
ab+ac
3.下列运算过程中,有错误的个数是( )
① ;
②-4×(-7)×(-125)=-(4×125×7);
③ ;
④[3×(-25)]×(-2)=3×[(-25)×(-2)]
A.1 B.2 C.3 D.4
A
小试牛刀
4.三个有理数相乘,积为负数,则其中负因数有( )个.
A.1 B.2 C.3 D.1或3
5.已知a,b,c为非零有理数,下列情况中,它们的积一
定为正数的是( )
A.a,b,c同号 B.a>0,b与c同号
C.b<0,a与c同号 D.a>b>0>c
D
B
小试牛刀
6. =[(-0.125)×(-8)]× ,
运算中运用的运算律是( )
A.乘法交换律 B.乘法结合律
C.分配律 D.乘法交换律和乘法结合律
D
7.已知有理数a,b,c在数轴上的对应点的位置如图所示,
则必有( )
A.abc>0 B.a(b-c)>0
C.(a+b)c>0 D.(a-c)b>0
B
小试牛刀
(1)2×(-1)× (2)
(3)(-1.2)×5×(-3)×(-4)
解:=2×1×
=1
解:
解:=-1.2×5×3×4
=-72.
8.计算:
课堂小结
课堂小结
1、乘法的交换律、结合律只涉及一种运算,而分配律要涉及两种运算.
2、分配律还可写成: ab+ac=a(b+c), 利用它有时也可以简化计算.
3、字母a、b、c可以表示正数、负数,也可以表示零,即a、b、c可以表示任意有理数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
