人教版(新)七上-1.4.1 有理数的乘法 第一课时【优质课件】
文档属性
| 名称 | 人教版(新)七上-1.4.1 有理数的乘法 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 14:27:48 | ||
图片预览









文档简介
(共37张PPT)
1.4.1 有理数的乘法
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我们已经熟悉正数及0的乘法运算.与加法类似,引入负数后,将出现 3×(-3),(-3)×3(-3)×(-3)这样的乘法.该怎样进行这一类的运算呢?
这就是我们本节课要学习的内容.
新课精讲
探索新知
1
知识点
有理数的乘法
0
一只蜗牛沿直线l爬行, 它现在的位置恰在l上的点O
l
我们借助数轴来探究有理数的乘法的法则
探索新知
问题:(1)如果蜗牛一直以每分2cm的速度向右爬行, 3分钟后
它在什么位置?
0
2
4
6
3分钟后蜗牛应在l上点O右边6cm,这可以表示为
(+2)×(+3)=+6 ①
l
探索新知
0
-2
-4
-6
-8
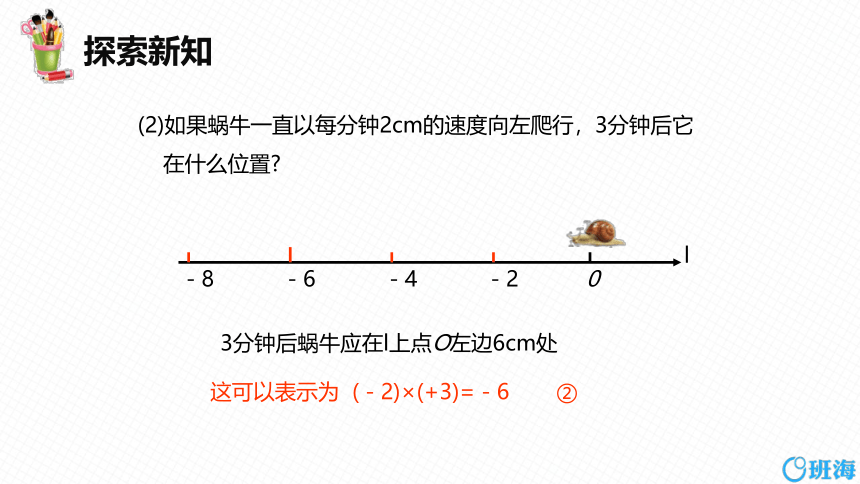
3分钟后蜗牛应在l上点O左边6cm处
(2)如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它
在什么位置
这可以表示为 (-2)×(+3)=-6 ②
l
探索新知
0
-2
-4
-6
-8
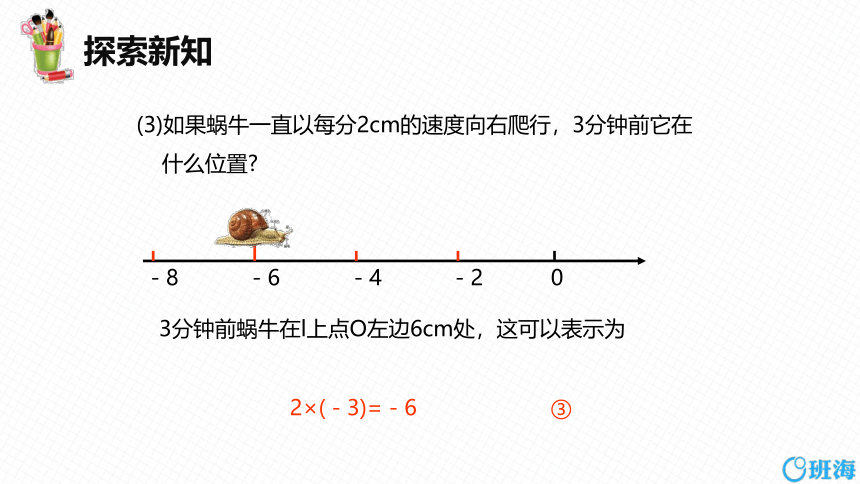
(3)如果蜗牛一直以每分2cm的速度向右爬行,3分钟前它在
什么位置
3分钟前蜗牛在l上点O左边6cm处,这可以表示为
2×(-3)=-6 ③
探索新知
(4)如果蜗牛一直以每分钟2cm的速度向左爬行,3分
钟前它在什么位置
0
2
4
6
3分钟前蜗牛应在l上点O右边6cm处,这可以表示为
(-2)×(-3)=+6 ④
探索新知
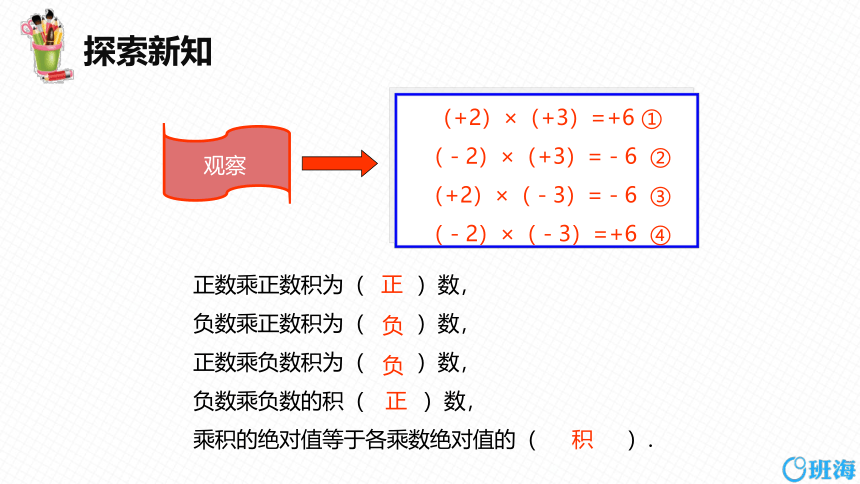
(+2)×(+3)=+6 ①
(-2)×(+3)=-6 ②
(+2)×(-3)=-6 ③
(-2)×(-3)=+6 ④
正数乘正数积为( )数,
负数乘正数积为( )数,
正数乘负数积为( )数,
负数乘负数的积( )数,
乘积的绝对值等于各乘数绝对值的( ).
正
负
负
正
积
观察
探索新知
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值
相乘任何数同0相乘,都得0.
任何数与1相乘都等于它本身,任何数与-1相
乘都等于它的相反数.
探索新知
例1 计算:(1)(-6)×(+5); (2)
(3) (4)
导引:(1)(3)异号两数相乘,积为负;(2)同号两数相乘,积为
正;(4)任何数与0相乘,都得0.
解: (1)(-6)×(+5)=-6×5=-30.
(2)
(3)
(4)
探索新知
例2 计算:
(1) (-3)×9; (2) 8×(-1);
解:=-27
要得到一个数的相反数,只要将它乘 -1.
解: =-8
解: =1
探索新知
总 结
先定符号,同号得正,异号得负,再算
绝对值;任何数与0相乘都得0.
探索新知
例3 如图,数轴上A、B两点所表示的两个数的( )
A.和为正数 B.和为负数
C.积为正数 D.积为负数
导引:由图可知A点表示的数是负数,B点表示的数为正数,并
且这两个数的绝对值相等.
D
探索新知
总 结
本题是一道数形结合题,先确定A、B两点表示的有理数的符号,再确定它们的绝对值大小,积的符号由两数的符号确定;两数的和的符号既要看两数的符号,又要看它们的绝对值的大小.本题体现了数形结合思想.
典题精讲
1.计算(-6)×(-1)的结果等于( )
A.6 B.-6 C.1 D.-1
2.计算:(-2)×3的结果是( )
A.-6 B.-1 C.1 D.6
A
A
3.计算:3-2×(-1)=( )
A.5 B.1 C.-1 D.6
A
典题精讲
4.计算:
=-54
=-24
=6
=0
探索新知
2
知识点
倒数
找特点,给这些数起一个你喜欢的名字.
1
1
1
你还能写出一些乘积为1的算式吗?
认真观察每一对数,
你发现了么?
两个乘数的分子
分母互相颠倒.
探索新知
如果两个数的乘积是1,那么我们称其中一个数是另一个数的倒数,并称这两个数互为倒数.
定义:
要点精析:
(1)0没有倒数.
(2)一个数和它的倒数的符号相同,即正数的倒数 是正数,负数的倒数是负数.
(3)倒数是相互的,当ab=1时,a叫做b的倒数,b也叫做a的倒数.
(4)1或-1的倒数是它本身.
探索新知
例4 求下列各数的倒数:
(1)- ;(2)-1;(3)- ;(4)0.125;(5)-1.4.
导引:根据定义,要求a(a≠0)的倒数,只要求 即可.
探索新知
总 结
(1)求小数的倒数,要先把小数化成分数,求带分数的倒数,要先把带分数化成假分数.
(2)互为倒数的两个数的符号相同,即正数的倒数一定是正数,负数的倒数一定是负数,记住这个结论,可以防止发生符号错误.
(3)0没有倒数;倒数等于本身的数有两个:±1.
探索新知
例5 已知a的倒数是它本身,b是-10的相反数,负数c的绝
对值是8,求式子4a-b+3c的值.
解: 因为a的倒数是它本身,所以a=±1.
因为b是-10的相反数,所以b=10.
因为负数c的绝对值是8,所以c=-8.
所以4a-b+3c=4×1-10+3×(-8)
=4-10+(-24) =-30.
或4a-b+3c=4×(-1)-10+3×(-8)
=-4-10+(-24) =-38.
典题精讲
1.若数a≠0,则a的倒数是____,___没有倒数;倒数等于它本身
的数是________.
2.若a与b互为相反数,c与d互为倒数,则5(a+b)-6cd=____.
0
1或-1
-6
4.-2015的倒数是( )
A.- B. - C.-2015 D.2015
3.- 的倒数的相反数等于( )
A.- 2 B. C. D.2
B
D
学以致用
小试牛刀
1.有理数乘法法则:两数相乘,同号得____,异号得____,并把
________相乘.任何数与0相乘,都得____.由此可得:如果两
数的积为正数,那么这两个数____________;如果两数的积为负
数,那么这两个数_________.一个数与-1相乘,得原数的相反数.
正
负
绝对值
0
同正或同负
一正一负
2.乘积是______的两个数互为倒数;______没有倒数;倒数等于它
本身的数是________.
1
0
±1
小试牛刀
3.-2的倒数是( )
A.- B. C.-2 D.2
A
4.下列各对数互为倒数的是( )
A.4和-4 B.-3和
C.-2和- D.0和0
C
小试牛刀
5.一个有理数和它的相反数之积( )
A.符号必为正 B.符号必为负
C.一定不大于0 D.一定不小于0
6.已知有理数a,b在数轴上对应点的位置如图所示,则ab的结果是( )
A.正数 B.负数 C.零 D.无法确定
C
B
小试牛刀
7.下列说法正确的是( )
①两个正数中,倒数大的反而小;
②两个负数中,倒数大的反而小;
③两个有理数中,倒数大的反而小;
④两个符号相同的有理数中,倒数大的反而小.
A.①②④ B.① C.①②③ D.①④
A
小试牛刀
8.计算:
(1)(+4)×(-5); (2)(-0.125)×(-8);
(3) × ; (4)0×(-13.52).
解:=-20
解: =1
解: = ×
=-1
解: =0
小试牛刀
9.计算:
(1)(-4)×(-8)-(-5)×|-7|
(2)
=32+35=67;
小试牛刀
10.已知|a|=3,|b|=4,且a+b<0,求ab的值.
解: 因为|a|=3,|b|=4,所以a=±3,b=±4.
又因为a+b<0,所以a=±3,b=-4.
当a=3,b=-4时,ab=3×(-4)=-12;
当a=-3,b=-4时,ab=(-3)×(-4)=12.
综上,ab的值为12或-12.
小试牛刀
11.一辆出租车在一条东西走向的大街上营运.一天上午,这辆车一共连续送客10次,其中4次向东行驶,每次行驶10 km;6次向西行驶,每次行驶7 km.问:
(1) 该出租车连续送客10次后,停在出发点的什么地方?
(2) 该出租车一共行驶了多少千米?
解:
(1)规定向东为正,则4×10+6×(-7)=-2(km).
所以该出租车停在出发点的西边2 km处.
(2)该出租车一共行驶了4×10+6×7=82(km).
课堂小结
课堂小结
两个数相乘,先确定积的符号,同号得正,异号得负,再把绝对值相乘;任何数与0相乘都得0.
倒数的求法技巧:
(1)求分数的倒数时,只要把这个分数的分子、分母颠倒位置即可(整数看成分母为1的分数);
(2)求带分数的倒数时,要先将其化成假分数;
(3)求小数的倒数时,要先将其化成分数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.4.1 有理数的乘法
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我们已经熟悉正数及0的乘法运算.与加法类似,引入负数后,将出现 3×(-3),(-3)×3(-3)×(-3)这样的乘法.该怎样进行这一类的运算呢?
这就是我们本节课要学习的内容.
新课精讲
探索新知
1
知识点
有理数的乘法
0
一只蜗牛沿直线l爬行, 它现在的位置恰在l上的点O
l
我们借助数轴来探究有理数的乘法的法则
探索新知
问题:(1)如果蜗牛一直以每分2cm的速度向右爬行, 3分钟后
它在什么位置?
0
2
4
6
3分钟后蜗牛应在l上点O右边6cm,这可以表示为
(+2)×(+3)=+6 ①
l
探索新知
0
-2
-4
-6
-8
3分钟后蜗牛应在l上点O左边6cm处
(2)如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它
在什么位置
这可以表示为 (-2)×(+3)=-6 ②
l
探索新知
0
-2
-4
-6
-8
(3)如果蜗牛一直以每分2cm的速度向右爬行,3分钟前它在
什么位置
3分钟前蜗牛在l上点O左边6cm处,这可以表示为
2×(-3)=-6 ③
探索新知
(4)如果蜗牛一直以每分钟2cm的速度向左爬行,3分
钟前它在什么位置
0
2
4
6
3分钟前蜗牛应在l上点O右边6cm处,这可以表示为
(-2)×(-3)=+6 ④
探索新知
(+2)×(+3)=+6 ①
(-2)×(+3)=-6 ②
(+2)×(-3)=-6 ③
(-2)×(-3)=+6 ④
正数乘正数积为( )数,
负数乘正数积为( )数,
正数乘负数积为( )数,
负数乘负数的积( )数,
乘积的绝对值等于各乘数绝对值的( ).
正
负
负
正
积
观察
探索新知
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值
相乘任何数同0相乘,都得0.
任何数与1相乘都等于它本身,任何数与-1相
乘都等于它的相反数.
探索新知
例1 计算:(1)(-6)×(+5); (2)
(3) (4)
导引:(1)(3)异号两数相乘,积为负;(2)同号两数相乘,积为
正;(4)任何数与0相乘,都得0.
解: (1)(-6)×(+5)=-6×5=-30.
(2)
(3)
(4)
探索新知
例2 计算:
(1) (-3)×9; (2) 8×(-1);
解:=-27
要得到一个数的相反数,只要将它乘 -1.
解: =-8
解: =1
探索新知
总 结
先定符号,同号得正,异号得负,再算
绝对值;任何数与0相乘都得0.
探索新知
例3 如图,数轴上A、B两点所表示的两个数的( )
A.和为正数 B.和为负数
C.积为正数 D.积为负数
导引:由图可知A点表示的数是负数,B点表示的数为正数,并
且这两个数的绝对值相等.
D
探索新知
总 结
本题是一道数形结合题,先确定A、B两点表示的有理数的符号,再确定它们的绝对值大小,积的符号由两数的符号确定;两数的和的符号既要看两数的符号,又要看它们的绝对值的大小.本题体现了数形结合思想.
典题精讲
1.计算(-6)×(-1)的结果等于( )
A.6 B.-6 C.1 D.-1
2.计算:(-2)×3的结果是( )
A.-6 B.-1 C.1 D.6
A
A
3.计算:3-2×(-1)=( )
A.5 B.1 C.-1 D.6
A
典题精讲
4.计算:
=-54
=-24
=6
=0
探索新知
2
知识点
倒数
找特点,给这些数起一个你喜欢的名字.
1
1
1
你还能写出一些乘积为1的算式吗?
认真观察每一对数,
你发现了么?
两个乘数的分子
分母互相颠倒.
探索新知
如果两个数的乘积是1,那么我们称其中一个数是另一个数的倒数,并称这两个数互为倒数.
定义:
要点精析:
(1)0没有倒数.
(2)一个数和它的倒数的符号相同,即正数的倒数 是正数,负数的倒数是负数.
(3)倒数是相互的,当ab=1时,a叫做b的倒数,b也叫做a的倒数.
(4)1或-1的倒数是它本身.
探索新知
例4 求下列各数的倒数:
(1)- ;(2)-1;(3)- ;(4)0.125;(5)-1.4.
导引:根据定义,要求a(a≠0)的倒数,只要求 即可.
探索新知
总 结
(1)求小数的倒数,要先把小数化成分数,求带分数的倒数,要先把带分数化成假分数.
(2)互为倒数的两个数的符号相同,即正数的倒数一定是正数,负数的倒数一定是负数,记住这个结论,可以防止发生符号错误.
(3)0没有倒数;倒数等于本身的数有两个:±1.
探索新知
例5 已知a的倒数是它本身,b是-10的相反数,负数c的绝
对值是8,求式子4a-b+3c的值.
解: 因为a的倒数是它本身,所以a=±1.
因为b是-10的相反数,所以b=10.
因为负数c的绝对值是8,所以c=-8.
所以4a-b+3c=4×1-10+3×(-8)
=4-10+(-24) =-30.
或4a-b+3c=4×(-1)-10+3×(-8)
=-4-10+(-24) =-38.
典题精讲
1.若数a≠0,则a的倒数是____,___没有倒数;倒数等于它本身
的数是________.
2.若a与b互为相反数,c与d互为倒数,则5(a+b)-6cd=____.
0
1或-1
-6
4.-2015的倒数是( )
A.- B. - C.-2015 D.2015
3.- 的倒数的相反数等于( )
A.- 2 B. C. D.2
B
D
学以致用
小试牛刀
1.有理数乘法法则:两数相乘,同号得____,异号得____,并把
________相乘.任何数与0相乘,都得____.由此可得:如果两
数的积为正数,那么这两个数____________;如果两数的积为负
数,那么这两个数_________.一个数与-1相乘,得原数的相反数.
正
负
绝对值
0
同正或同负
一正一负
2.乘积是______的两个数互为倒数;______没有倒数;倒数等于它
本身的数是________.
1
0
±1
小试牛刀
3.-2的倒数是( )
A.- B. C.-2 D.2
A
4.下列各对数互为倒数的是( )
A.4和-4 B.-3和
C.-2和- D.0和0
C
小试牛刀
5.一个有理数和它的相反数之积( )
A.符号必为正 B.符号必为负
C.一定不大于0 D.一定不小于0
6.已知有理数a,b在数轴上对应点的位置如图所示,则ab的结果是( )
A.正数 B.负数 C.零 D.无法确定
C
B
小试牛刀
7.下列说法正确的是( )
①两个正数中,倒数大的反而小;
②两个负数中,倒数大的反而小;
③两个有理数中,倒数大的反而小;
④两个符号相同的有理数中,倒数大的反而小.
A.①②④ B.① C.①②③ D.①④
A
小试牛刀
8.计算:
(1)(+4)×(-5); (2)(-0.125)×(-8);
(3) × ; (4)0×(-13.52).
解:=-20
解: =1
解: = ×
=-1
解: =0
小试牛刀
9.计算:
(1)(-4)×(-8)-(-5)×|-7|
(2)
=32+35=67;
小试牛刀
10.已知|a|=3,|b|=4,且a+b<0,求ab的值.
解: 因为|a|=3,|b|=4,所以a=±3,b=±4.
又因为a+b<0,所以a=±3,b=-4.
当a=3,b=-4时,ab=3×(-4)=-12;
当a=-3,b=-4时,ab=(-3)×(-4)=12.
综上,ab的值为12或-12.
小试牛刀
11.一辆出租车在一条东西走向的大街上营运.一天上午,这辆车一共连续送客10次,其中4次向东行驶,每次行驶10 km;6次向西行驶,每次行驶7 km.问:
(1) 该出租车连续送客10次后,停在出发点的什么地方?
(2) 该出租车一共行驶了多少千米?
解:
(1)规定向东为正,则4×10+6×(-7)=-2(km).
所以该出租车停在出发点的西边2 km处.
(2)该出租车一共行驶了4×10+6×7=82(km).
课堂小结
课堂小结
两个数相乘,先确定积的符号,同号得正,异号得负,再把绝对值相乘;任何数与0相乘都得0.
倒数的求法技巧:
(1)求分数的倒数时,只要把这个分数的分子、分母颠倒位置即可(整数看成分母为1的分数);
(2)求带分数的倒数时,要先将其化成假分数;
(3)求小数的倒数时,要先将其化成分数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
